基于Python的决策树配镜预测系统

陈群贤 上海电机学院高职学院

1 决策树（decision tree)

1.1 决策树算法的描述

决策树是分类和预测的挖掘方法中应用较为广泛的模式之一，是一种由内部结点、分叉及叶结点构成的，用来表示决策树规则的树结构，其中，内部结点表示某种检验属性，分叉表示检验的结果，叶结点表示类或某一类的分类，而顶点称为根结点。在构建的决策树中，从根节点到叶结点的一条路径就对应着一条分类规则，其构建的过程，取决于检验属性的选择以及分叉点的确定。不同决策树算法采用的属性分割法不同，常用的决策树算法主要有：ID3、C4.5、GINT等。

1.2 决策树构造过程所遵循的原则

如果把一个节点（非叶子节点）看做是提一个问题，那么原则就是：尽可能先提最重要的问题，通过最少的问题得到最多的信息。所以对于决策树来说，就是希望从根节点走到叶节点的决策路径越短越好。如果说把决策树中每一个非叶子节点看做是对样本的某个特征进行提问。那么我们可以这样认为：构造决策树，就是要正确地选择特征，使得决策树尽可能地矮。

如何用贪心法来构造一颗“矮”的决策树？我们在构造决策上并选择特征的时候，为了缩短决策路径，就需要让测试样本的不确定性尽可能地少。建立规则的过程如下：首先利用数据集根据特征属性计算信息增益，然后选择具有最大信息增益的特征属性作为根节点，以该特征属性的每个数值作为一个分支，最后根据特征属性的每个数值划分的数据集只包含一个数值或者只包含一个特征属性为止。

1.3 信息熵

用贪心法来构造一颗“矮”的决策树时用到的熵，香农熵（Shannon’s Entropy）又简称为熵(Entropy)，是对不确定性的测量，数据集包含的类别越多，对应信息熵越大；设随机变量X的取值范围是{x1,x2,…,xn)，则X的熵H定义为：

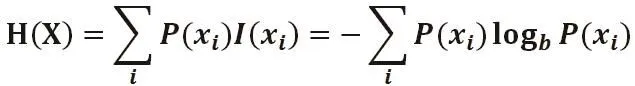
这里b是对数所使用的底数，通常是2；p(xi)是选择该分类的概率。

1.4 决策树归纳算法（ID3）

1970-1980 ，J.Ross. Quinlan首先提出ID3算法，第一步是选择属性判断结点，采用信息熵的比较。第二步是信息增益(Information Gain)：Gain(A)=Info(D)-Infor_A(D)通过A来作为节点分类获取了多少信息。ID3 算法以信息增益作为特征属性选择的依据，导致数值类型多的特征属性比数值类型少的特征属性具有更高的信息增益。

信息增益 (Information Gain)：Gain(A)=Info(D)-Infor_A(D)。

2 决策树算法

2.1 决策树算法的形式化描述

决策树算法的形式化描述如下：

1)起初只是一颗空树以及一些经过处理的数据样本的集合，在进行数据分配时，选取最优的根节点，还要选取测试的属性，然后再对样本中的数据进行划分；

2)如果当前的样本集合中的属性属于同一种类别，那么就只创建本类别的叶子节点；

3)如果不是同一属性，则就选取最优的计算方法计算当前集合的任何的可能划分方法；

4)将用最优划分所对应的属性当作节点的属性，而且创建和该属性含有一样多的子节点；

5)根据所选的属性的值作为节点的条件，而且将节点当中的父节点所对应的样本集合划分为每个子节点当中；

6)再将分支的节点当作当前的节点，然后从步骤（2）如此循环，指导最后划分彻底为止。

2.2 决策树算法的流程图

决策树算法的流程图如图1所示.

图1 决策树算法的流程图

3 根据ID3算法构造配镜预测系统决策树

3.1 数据集合

本次测试的模拟数据如表1所示。数据包含患者的年龄、视力诊断结果、闪光程度、泪流量等四个特征属性以及选好的眼镜类型。其中：

患者年龄 age：young、pre、presbyopic

患者视力诊断结果prescript：myope、hyper

患者闪光程度astigmatic：yes、no

患者流泪症状tearRate：normal、reduced

隐形眼镜类型：no lenses(不需要镜片)、hard(硬型镜片)、soft(软型镜片)

表1 测试模拟数据

3.2 配镜预测系统决策树归纳算法

例如tearRate的信息增益，Gain(tearRate) = Info(type_lenses) - Infor_tearRate (type_lenses)。

Info(type_lenses)是这24个记录中，no lenses的概率15/24，soft的概率5/24，hard的概率4/24，带入到信息熵公式。

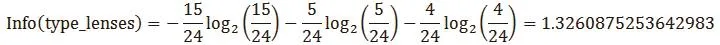
Infor_tearRate (type_lenses)是tearRate属性中normal的概率是12/24，其中no lenses的概率3/12，soft的概率5/12，hard的概率4/12；reduced的概率是12/24，其中no lenses的概率12/12，soft的概率0/12，hard的概率0/12，分别代入信息熵公式：

Info(type_lenses)与Infor_tearRate (type_lenses)做差，即是tearRate的信息增益，具体如下：

G a i n(t e a r R a t e)=I n f o(t y p e_l e n s e s)-I n f o r_t e a r R a t e (t y p e_l s e s)=1.3 2 6 0 8 7 5 2 5 3 6 4 2 9 8 3-0.7772925846688997=0.5487949406953986

类似，Gain(age) = 0.03939650364612124, Gain(prescript) =0.039510835423565815, Gain(astigmatic)= 0.37700523001147723

在配镜预测系统中，比较发现tearrate特征可以使熵下降得最快，所以，选择信息增益最大的tearRate作为根节点。

重复计算即可。

3.3 算法结果图

根据ID3算法，选择信息增益最高的属性tearRate，即选择类流量作为决策树的根节点，其他过程依次类推。通过Python实现ID3算法，利用训练样本构造的决策树文本方式是：

{`tearRate`： {`normal`： {`astigmatic`： {`no`： {`age`：{`presbyopic`： {`prescript`： {`hyper`： `soft`, `myope`： `no lenses`}}, `young`： `soft`, `pre`： `soft`}}, `yes`： {`prescript`：{`hyper`： {`age`： {`presbyopic`： `no lenses`, `young`： `hard`,`pre`： `no lenses`}}, `myope`： `hard`}}}}, `reduced`： `no lenses`}}

采用文本方式很难分辨出决策树的摸样，调用dtPlot.createPlot(lensesTree)函数，可将决策树可视化展现如图2所示。

图2 隐形眼镜配型决策树

4 结束语

本文展现了决策树在隐形眼镜配型预测系统中的应用，挖掘出对配镜具有指导性的潜在规律，具有一定的现实意义。利用已经积累的信息，通过决策树算法可以挖掘出眼科医生对隐形眼镜配型的决策过程，帮助非专业用户判断隐形眼镜类型的选配。