基于负荷点聚类分区的配电网网架规划方法

肖白，郭蓓，姜卓，施永刚，焦明曦

(1．东北电力大学电气工程学院，吉林省吉林市 132012；2．北华大学计算机科学技术学院，吉林省吉林市 132021；3．国网吉林省电力有限公司通化供电公司，吉林省通化市 134001；4．国网吉林省电力有限公司长春供电公司，长春市 130021)

0 引 言

配电网是电力系统的重要组成部分，其规划结果直接影响配电网的投资、收益及未来年配电网运行的安全性、经济性和稳定性[1]。网架规划在配电网规划过程中起着承上启下的关键作用，一直是国内外学者的研究重点。

网架规划是在满足未来负荷增长需求以及相关约束条件下，获得经济性和可靠性目标最优的网架方案。文献[2-3]以年投资和运行综合成本最小为优化目标进行网架规划。文献[4]通过“成本-效益分析法”和反向传播算法获得配电网的多阶段规划方案。但上述研究没有充分考虑网架方案的可靠性，对此，有学者提出了网架风险指标[5]和网络结构抗毁性指标[6-7]等可靠性指标，并将其引入到网架规划模型的目标函数中，以提高网架方案的可靠性。接入分布式电源和设置联络线也是提高网架可靠性的有效措施，学者对含分布式电源的网架规划模型[8-9]和联络线规划模型[10-11]开展了研究。但文献[10-11]的联络线规划模型没有区分不同的负荷转供情况对停电成本的影响，且没有考虑联络线的投资成本。

以上一次性考虑所有负荷点的网架规划方法存在模型的决策变量过多，求解难度大的问题，对此，有学者提出了先分区再进行网架规划的方法。文献[12]先对区域内的变电站进行所属供电块划分，为变电站之间的联络线优化奠定基础。文献[13]考虑到变电站出线数量有限的问题，将其供电范围划分为与出线数量相同的区域，并对每个区域进行先主干后支路的网架规划。文献[14]按照一定的负荷大小将变电站的供电区域进行划分，然后获得变电站与虚拟负荷点之间建设总成本最小的网架方案，但最终的辐射状网架可靠性不足。文献[15]采用基于勒贝格公式的聚类算法对负荷点分区，并将聚类中心作为等效负荷点，进行各分区的主次级网架和各分区内的联络线规划，但文中没有考虑到负荷分布不均匀对分区的影响，出现了一些分区负荷较重而一些分区负荷较轻的情况，不利于系统的经济运行，并且没有对初始聚类中心进行优化。

针对一次性计及所有负荷点的网架规划模型的决策变量过多，现有负荷点聚类分区方法没有考虑负荷分布不均匀的影响和初始聚类中心的优化等问题，本文首先提出用负荷权重改进K-means聚类算法，并通过Huffman树算法优化初始聚类中心，对变电站供电范围内的负荷点进行聚类，将每一类作为一个负荷点分区；然后建立计及地理因素的年综合成本最小的主网架规划模型；最后为提高网架的可靠性进行各负荷点分区之间的联络线规划，根据负荷是否可被转供对停电成本采取不同的计算方法，使方案更加合理；同时构建连接关系矩阵以提高线路的年运行成本和年停电成本的计算效率。通过算例验证本文所提方法的可行性。

1 基于改进K-means聚类算法的负荷点聚类分区

1.1 负荷权重

当配电网中负荷分布不均时，仅通过欧式距离最小原则对负荷点进行聚类分区，可能会出现部分区域轻载部分区域重载而导致系统运行不经济的问题，同时还会使区域之间联络线的备用容量增大，投资成本增加。因此，本文提出用负荷权重对K-means聚类算法进行改进，以有效解决由于负荷分布不均匀引起的各负荷点分区之间的负荷相差较大的问题。

第j个负荷点的负荷权重αj使用公式(1)计算：

(1)

式中：j为负荷点编号，j=1，…，Nnode，Nnode为待规划区域内的负荷点总数；pj为第j个负荷点的负荷大小；l为负荷点分区的编号，l=1，…，n，n为待规划区域内的负荷点分区总数；Sl为向第l个负荷点分区供电的线路的最大允许负载容量； cosφl为向第l个负荷点分区供电的线路的功率因数；PΣl为前一次聚类时第l个负荷点分区所累积的总负荷。

负荷权重综合考虑了向该负荷点分区供电的线路的最大允许负载容量和负荷点分区在前一次聚类时所累积的负荷总量的影响。负荷权重的引入可增大负荷密度较小区域的分区的负荷点个数，减小负荷密度较大区域的分区的负荷点个数，从而在一定程度上实现各负荷点分区之间的负荷相对均匀。

1.2 基于改进K-means聚类算法进行负荷点聚类分区的步骤

在进行负荷点聚类分区时考虑满足以下条件：各负荷点分区之间的负荷尽可能均匀，以保证系统运行的经济性和减小联络线的备用容量；各负荷点分区内的负荷总量应不超过为其供电的线路的允许最大负载容量，以保证系统运行的安全性。考虑到K-means聚类算法的聚类结果在一定程度上受到初始聚类中心的影响，本文采用Huffman树算法优化选择初始聚类中心。利用改进K-means聚类算法进行负荷点聚类分区的主要步骤如下详述。

(1)确定负荷点的聚类分区数：根据待规划区域各变电站供电范围内的总负荷和馈线的允许最大负载容量，由公式(2)计算各变电站供电范围内的负荷点聚类分区数n。

(2)

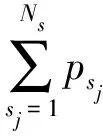
(2)选择初始聚类中心：根据Huffman树算法的思想和负荷点聚类分区的实际需要，用负荷点之间的欧式距离来构造数据相异度矩阵，并在生成Huffman树时将左右子树根节点的权值的均值作为新的二叉树根节点。对最终生成的Huffman树，按构造节点的逆序找到最后确定的n-1个节点，将这n-1个节点删除后Huffman树将被分为n棵子树，分别求这n棵子树所包含的负荷点的坐标均值即得到初始的n个聚类中心。

(3)对负荷点进行聚类分区：采用负荷权重对负荷点到各聚类中心的欧式距离进行修正，按照修正距离最小的原则对负荷点进行聚类，如式(3)所示，并将每一类作为一个负荷点分区。

(3)

式中：dlj为第l个负荷点分区的聚类中心和第j个负荷点之间的修正距离；αj为第j个负荷点的负荷权重，由公式(1)计算；(xl，yl)和(xj，yj)分别为第l个负荷点分区的聚类中心和第j个负荷点的位置坐标。开始迭代时，负荷点的负荷权重的初值设置为1。

(4)负荷点分区的总负荷校验：负荷点完成聚类分区后，应校验其所属的负荷点分区内的总负荷是否在馈线允许的最大负载容量范围内，若是，则进行下一步；否则，将该负荷点划分至相邻的有功容量裕度大于该点负荷值的分区内。

(5)确定新的聚类中心：当所有负荷点完成聚类分区之后，计算各负荷点分区内的负荷点的位置中心，并将其作为下一次迭代的初始聚类中心。

(6)重复步骤(3)至步骤(5)，直到相邻两次聚类的中心或负荷点划分的变化小于要求的精度为止。

(7)计算各负荷点分区内的负荷点与变电站之间的距离，并将距离最小的负荷点定义为各负荷点分区的“源负荷点”。

2 连接关系矩阵

为快速计算流过支路i的电流得到其有功损耗和运行成本，以及快速判断联络线的位置对故障支路下游负荷转供情况的影响，本文建立了根据功率流向表示负荷点上下游关系的连接关系矩阵G。

2.1 连接关系矩阵的构建

连接关系矩阵G仅由0和1元素构成，G的行和列均与负荷点对应，G的元素确定原则如下：无论负荷点j与k是否直接相连，只要功率从负荷点j流向k，即负荷点k在j的下游，则Gjk=1，否则Gjk= 0。连接关系矩阵中某一行的非零元素所在列对应的负荷点构成了该行节点的下游负荷点集合，某一列的非零元素所在的行对应的负荷点构成了该列节点的上游负荷点集合。图1中，负荷点11，10，1，2，3，4，9，22属于同一负荷点分区并由同一条10 kV馈线供电，负荷点11直接与变电站相连，功率流向为变电站→11→10→1→2→3→4和变电站→11→9→22，根据连接关系矩阵的构建原则得到负荷点11，10，1，2，3，4，9，22的连接关系矩阵G1，如式(4)所示。对于负荷点11，所有负荷点均为其下游负荷点，故其所在行的所有元素均为1；对于负荷点22，其所在列有3个非零元素，非零元素对应行的负荷点分别为11、9、22，故其上游负荷点集合为{11,9,22}。

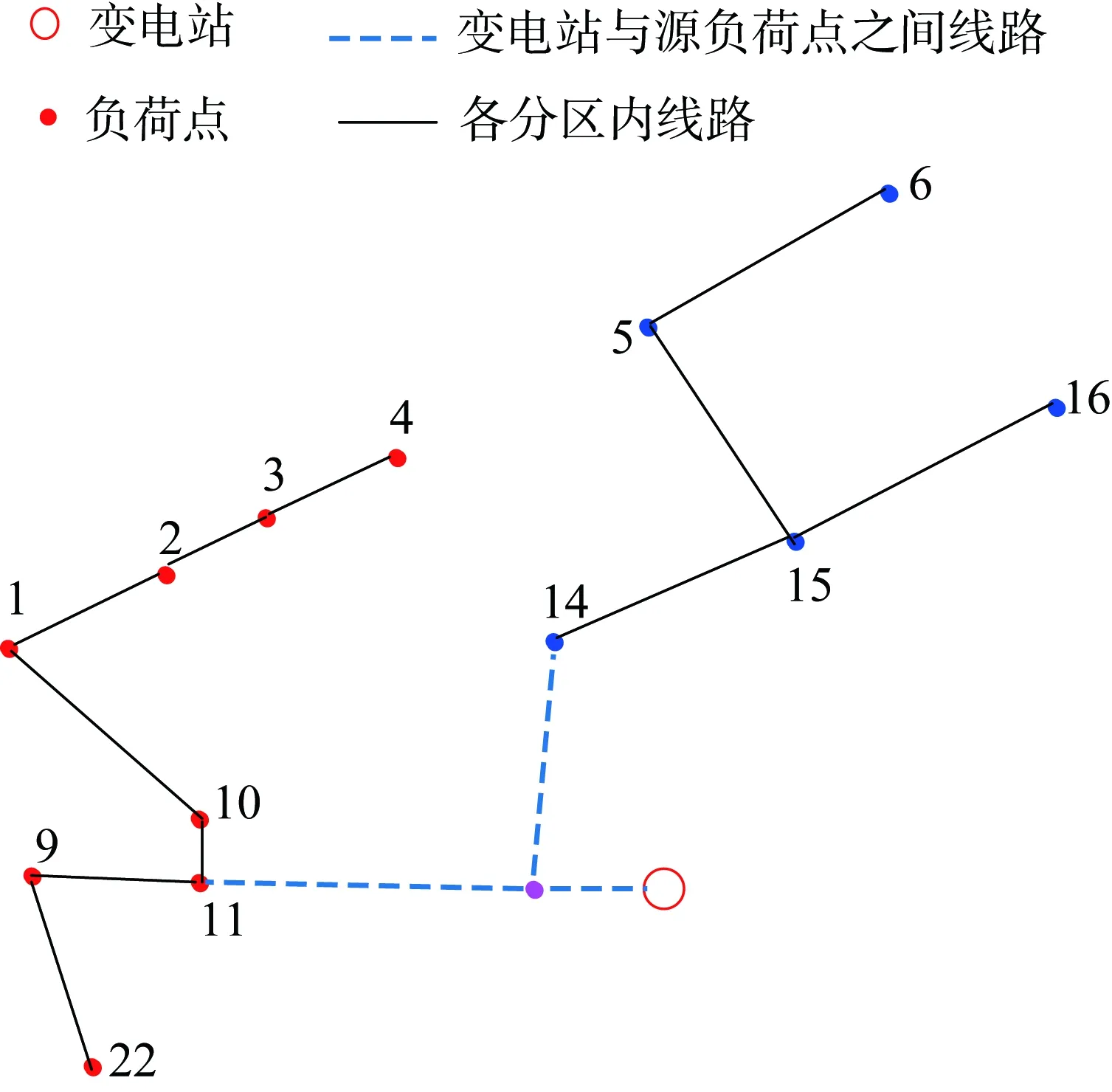
图1 负荷点的连接关系示意图Fig.1 Diagram of load node connections

(4)

2.2 基于连接关系矩阵的支路电流计算

由连接关系矩阵G右乘负荷列向量p便可求得任意负荷点的下游总负荷，进而得到以该负荷点为末端节点的支路i的下游总负荷，用以快速计算支路i上流过的电流Ii。

(5)

(6)

式中：P∑为各负荷点的下游总负荷列向量；G为连接关系矩阵；p为负荷点的负荷列向量；βi为支路i的下游负荷点集合；UNi为支路i的额定电压；cosφj为负荷点j的功率因数；Pi为支路i的下游总负荷，是各负荷点的下游总负荷列向量P∑中的元素；cosφi为支路i的功率因数。

2.3 基于连接关系矩阵的故障支路下游负荷转供情况判断

联络线的位置对故障支路下游负荷的转供有直接影响，因而需要分情况对故障支路下游负荷的停电成本进行计算。根据网架的连接关系矩阵和联络线的位置得到联络线的两端节点各自的上游负荷点集合，由此快速判断故障支路下游负荷是否可被转供，具体判断过程如下详述。

若某故障支路的两端节点均属于联络线某端节点的上游负荷点集合，则该支路发生故障时可实现全部或部分下游负荷的转供；若某故障支路的两端节点均不属于联络线某端节点的上游负荷点集合或仅有一端节点属于联络线某端节点的上游负荷点集合，则该支路发生故障时其下游负荷将不可被转供；由此得到支路故障时其下游负荷可被转供的支路集合和支路故障时其下游负荷不可被转供的支路集合，用于不同情况下的停电成本计算。

在图1中，当两负荷点分区(负荷点11，10，1，2，3，4，9，22组成的负荷点分区1和负荷点14，15，16，5，6组成的负荷点分区2)之间的待选联络线的位置为4—15时，根据负荷点的连接关系矩阵得到联络线的两端节点4和15的上游负荷点集合分别为{11,10,1,2,3,4}和{14,15}。当故障支路为2—3时，因端节点2和3均属于联络线端节点4的上游负荷点集合，所以故障支路2—3的下游负荷可被转供；当故障支路为5—6时，因端节点5和6均不属于联络线端节点15的上游负荷点集合，所以故障支路5—6的下游负荷不可被转供。

3 网架规划的数学模型

完成对负荷点的聚类分区后，本文首先建立变电站与“源负荷点”之间以及各负荷点分区内的主网架规划模型，然后为提高网架方案的可靠性建立了各负荷点分区之间的联络线规划模型。

3.1 主网架规划模型

针对工程实践中部分线路会不可避免地经过山岭、河流和跨越高速公路等问题，本文提出用地理障碍因子量化不利地理因素对网架规划方案的影响，建立计及地理因素的年投资和运行成本最小的主网架规划模型，目标函数如下：

(7)

式中：f为网架规划的年总成本；fI为网架的年投资成本；fO为网架的年运行成本。

(1)网架的年投资成本：

(8)

式中：r0为年利率；Ti为支路i的使用寿命周期；xi为支路i的决策变量，新建为1，否则为0；Ct,i为t类型的支路i单位长度的投资成本；ki为支路i的曲折系数；Li为支路i的长度；ADi为地理障碍因子，当支路i不经过地理障碍区域时为1，当支路i经过有地理障碍区域时则根据现场经验取不同的值。

(2)网架的年运行成本：

(9)

(10)

式中：C0为网损电价；ΔPi为支路i的有功损耗；τmax,i为支路i的年最大负荷损耗小时数；Ii为流过支路i的电流，由式(5)和式(6)计算；Ri为支路i单位长度的电阻。

约束条件：

(1)节点电压约束：

Ujmin≤Uj≤Ujmax

(11)

式中Ujmin和Ujmax分别为系统正常运行时节点j允许的电压下限值和上限值。

(2)支路电流约束：

0≤Ii≤Iimax

(12)

式中Iimax为系统正常运行时支路i上允许流过的电流上限值。

(3)网络的辐射性约束：保证系统正常运行时无环路。

(4)网络的连通性约束：保证所有的负荷点都能得到可靠供电。

3.2 联络线规划模型

系统运行过程中当支路发生故障时，联络线对于故障支路下游负荷的供电恢复起着至关重要的作用，因此在供电可靠性要求较高的地区，联络线的设置是网架规划的必须环节。

本文以支路发生故障时配电网运营商对用户的年停电赔偿成本和因少售电产生的年停电损失成本之和作为年停电成本，建立年投资和年停电成本最小的联络线规划模型，目标函数如下：

(13)

式中：fTie为联络线规划的年总成本；fTI为联络线的年投资成本；fTR1为支路发生故障时其下游负荷可被转供情况下的年停电成本；fTR2为支路发生故障时其下游负荷不可被转供情况下的年停电成本。

(1)联络线的年投资成本：

(14)

式中：t为联络线编号，t=1，…，m，m为各负荷点分区之间设置的联络线的总条数；r0为年利率；Tt为联络线t的使用寿命周期；xt为联络线t的决策变量，新建为1，否则为0；Ct,t为t类型的联络线t单位长度的投资成本；kt为联络线t的曲折系数；Lt为联络线t的长度；ADt为地理障碍因子，当联络线t不经过地理障碍区域时为1，当联络线t经过有地理障碍区域时则根据现场经验取不同的值。

(2)支路故障时的年停电成本：

故障支路下游负荷在可被转供和不可被转供情况下的年停电成本计算如下：

1)若支路故障时联络线可转供其下游的全部负荷或部分负荷，则年停电成本由故障支路下游不可被转供的负荷在故障修复期间的年停电成本和可被转供的负荷在供电恢复期间的年停电成本组成，使用式(15)计算：

(15)

式中：λi为支路i单位长度的故障率，次/(km·年)；C2为配电网运营商对用户的赔偿电价与售电电价之和；Pt为联络线t的最大可转供负荷容量；Δt1为支路的平均故障修复时间；Δt2为可被转供的负荷恢复供电所需的平均时间。

2)若支路故障时联络线无法转供其下游负荷，则年停电成本由故障支路的下游负荷在故障修复期间的年停电成本组成，使用式(16)计算：

(16)

式中：Ωl2为第l个负荷点分区内的支路故障时其下游负荷不可被转供的支路集合。

约束条件：

(1)联络线的可转供负荷应在联络线允许的最大负载容量范围内；

(2)联络线的可转供负荷应不超过其上游供电线路的有功容量裕度的最小值。

4 基于改进最小生成树算法的主网架规划

将变电站和负荷点抽象为图的顶点，将各顶点间可能架设线路的走廊作为图的边，将各条线路的年投资和运行成本之和作为各边的权，将配电网规划论域转化为一个加权图[16-17]。

在网架确定之前无法得到线路的有功损耗及判断线路是否经过有地理障碍的区域，因此先不计网架的运行成本和地理因素的影响，仅以线路不经过地理障碍区域时的年投资成本作为各边的初始权值，由基本的最小生成树算法获得加权图的初始最小生成树。然后在后续迭代过程中计及线路的运行成本和地理因素的影响，动态更新各边权值，通过反复迭代最终得到总成本最小的规划方案。基于改进最小生成树算法的具体求解过程如下：

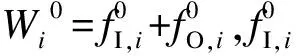
(2)使用Prim算法获得网络加权图的初始最小生成树T0。

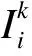
(4)将第kiter次迭代得到的最小生成树Tk之外的各条边的权值还原为初值，判断是否存在Tk以外的各条边的权值小于Tk中各条边权值的情况，若有，则将相应的边按权值从小到大的顺序放入集合Qv中；否则，退出，最小生成树Tk即为总成本最小的主网架规划方案。

(5)从集合Qv中按权值从小到大的顺序逐次取出一条边加入Tk中，并将由此形成的环路中权值最大的边删除，从而得到一棵新树TN。

根据以上步骤求解由式(7)—(12)确定的主网架规划模型得到的规划方案仅表明线路的走向和连接关系，还需参考相关部门的专家意见、结合规划区域内的市政建设与改造工程(规划新建电缆需要入廊时必须以地下综合管廊建设工程为依据)和规划区域街道的具体地形情况，以获得线路沿街道分布的规划方案。

5 算例分析

根据吉林省某待规划地区目标年的空间负荷预测结果和变电站的规划结果，采用本文提出的模型和方法进行网架规划。规划地区目标年的总负荷预测值为43.968 MW，负荷点的位置为各用电地块的位置中心，负荷点的详细信息见附表A1。

按照当地电网部门的要求，新建10 kV馈线采用型号为YJLV22-3×300的电缆；结合现场经验，设负荷点的功率因数为0.85；正常运行时线路允许的最大负载率为0.5；线路的曲折系数为1.5；电缆的寿命周期为40年；线路的年最大负荷损耗小时数为 4 000 h；线路单位长度的年故障率为0.1次/(km·年)；新建电缆的综合投资为100万元/km；线路单位长度的电阻为0.077 8 Ω/km；该区域的不利地理因素为河流，根据现场经验河流障碍因子取1.1；网损电价和售电电价均为0.6元/(kW·h)；该规划区域内工业负荷较多，故障停电时损失较大，赔偿电价取10元/(kW·h)；线路的平均故障修复时间为3 h；故障线路下游可被转供的负荷恢复供电所需的平均时间为0.25 h。

5.1 负荷点聚类分区的结果

采用本文提出的改进K-means聚类算法对负荷点进行聚类分区的结果见表1。

由表1可知，与文献[15]中方法(结果见附表A2)相比，本方法中得到的各负荷点分区之间的负荷分布更均匀，各负荷点分区之间的负荷值最大相差为1.203 MW，相邻负荷点分区之间的负荷值最大相差为1.203 MW(分区4和分区8)，而文献[15]中方法得到的各负荷点分区之间的负荷值最大相差为5.874 MW，相邻负荷点分区之间的负荷值最大相差为5.765 MW(分区4和分区8)。

负荷点分区之间的负荷分布越均匀越有利于系统的经济运行，并且当需要在相邻负荷点分区之间设置联络线以提高网架的可靠性时，为实现线路之间的互为备用，联络线的最小备用容量应由负荷较重的负荷点分区确定，相邻负荷点分区之间的负荷相差越小，联络线的备用容量越小，经济性越好。如需要在负荷点分区4和分区8之间设置联络线时，本文方法和文献[15]中所提方法得到的联络线最小备用容量分别为5.393 MW和6.798 MW，本方法中联络线的容量更小，方案的经济性更好。

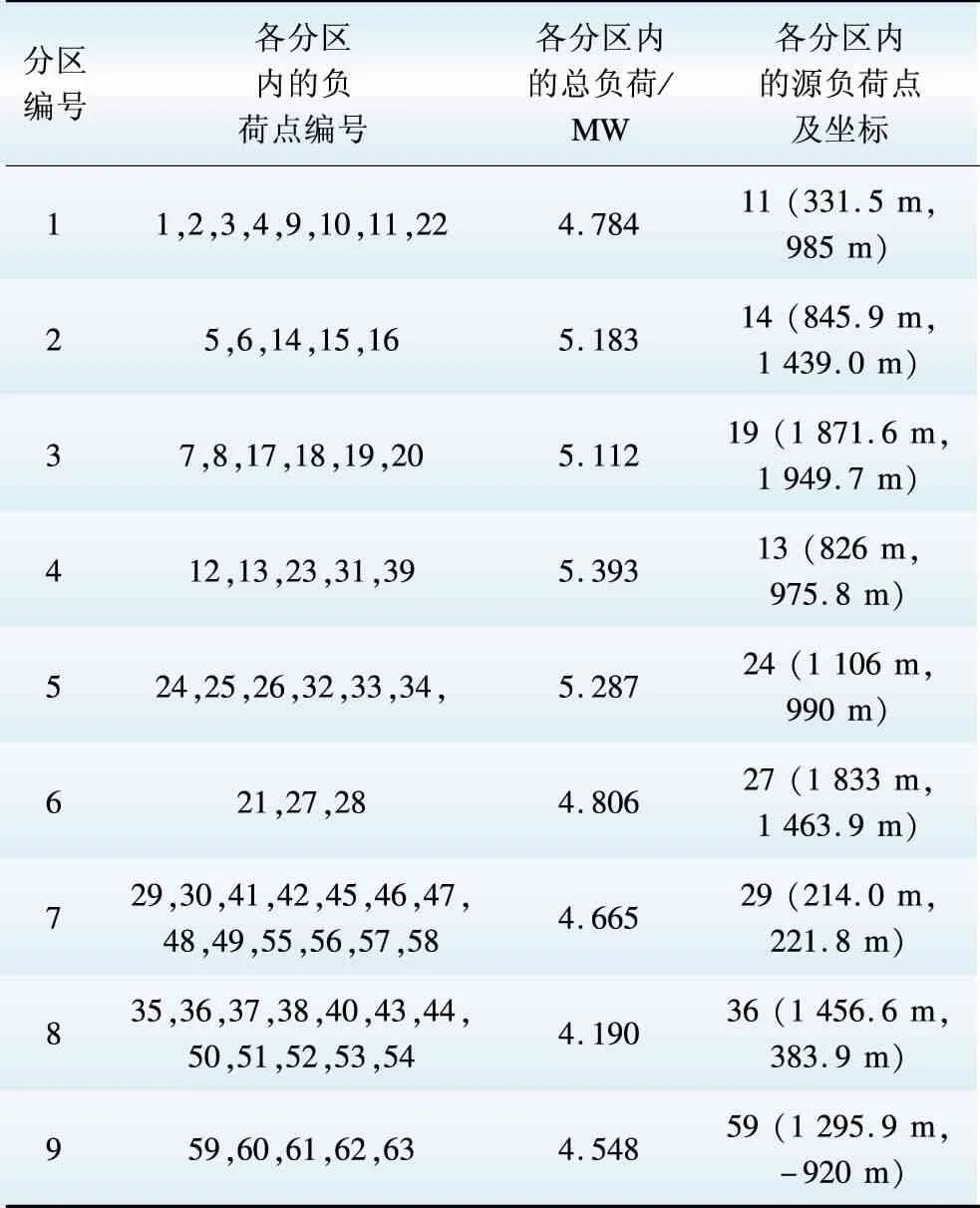
表1 负荷点聚类分区结果Table 1 Clustering blocks of load nodes

5.2 主网架规划方案

求解由式(7)—(12)确定的主网架规划模型，得到表明线路走向及连接关系的主网架规划方案见附图B1，主网架沿街道分布的规划方案见图2，主网架规划方案的各项成本见表2。

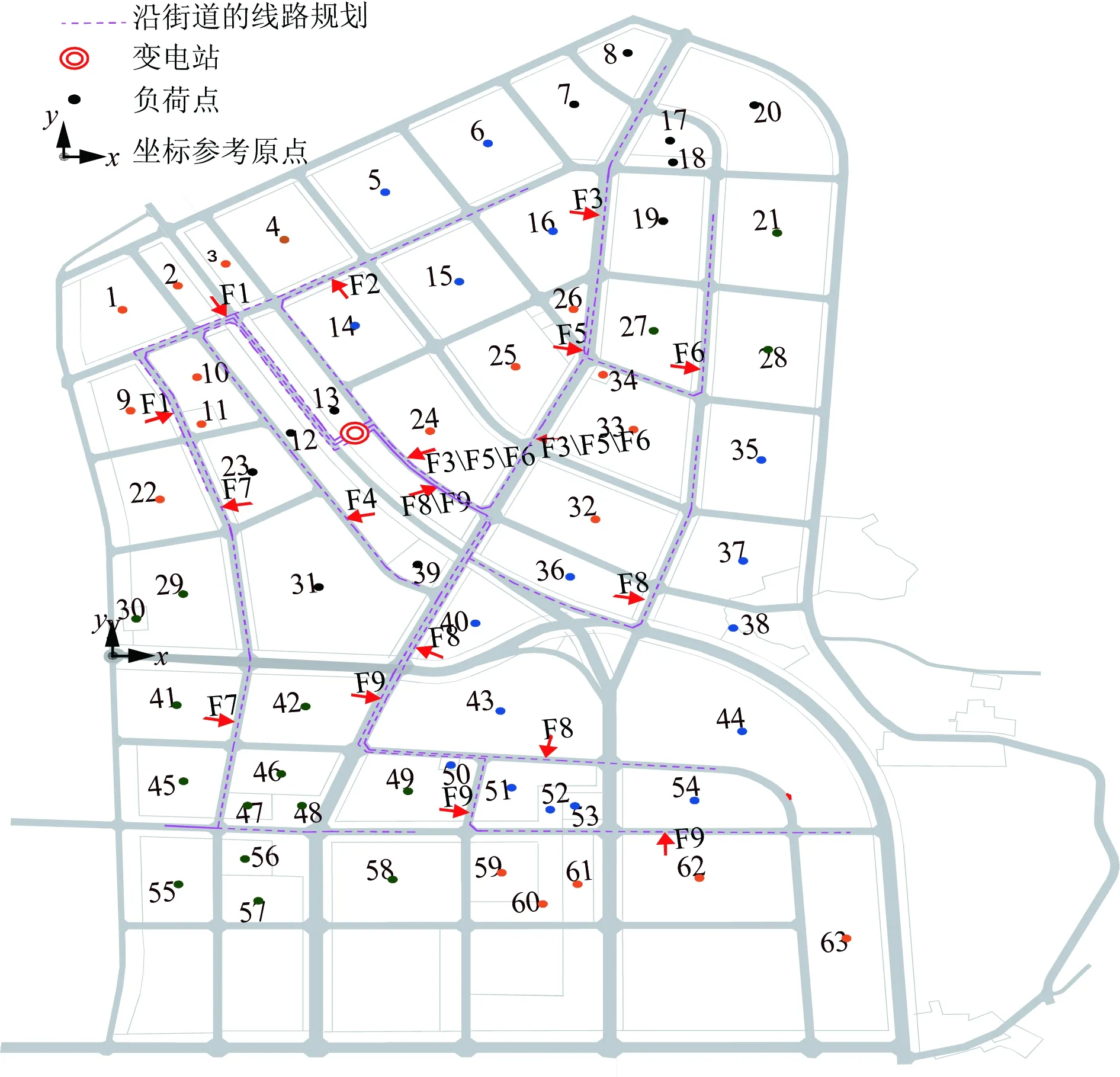
图2 主网架沿街道分布的规划方案Fig.2 Main network planning along street

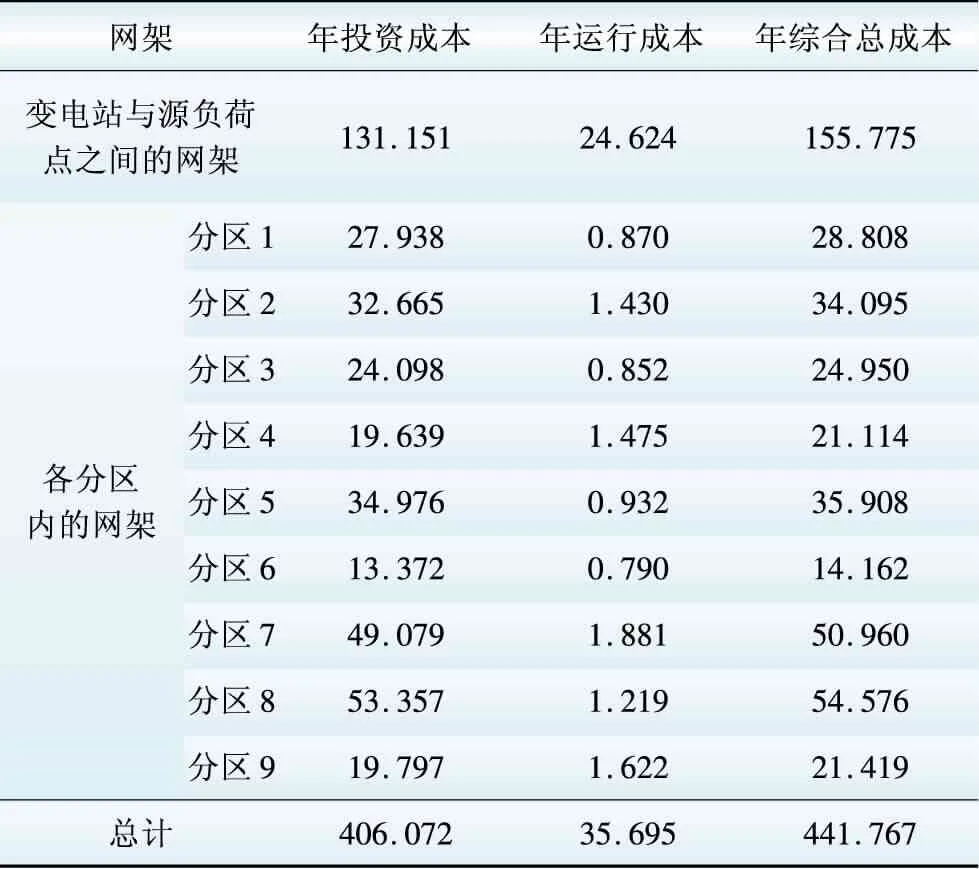
表2 主网架规划方案的各项成本Table 2 Cost of main network planning 万元/年

分析表2中主网架规划方案的各项成本可知，由于各负荷点分区内的负荷点位置相对集中，负荷点之间的支路的长度较短，且支路上流过的电流较小，故各负荷点分区内网架的各项成本都较低；而各负荷点分区内的“源负荷点”与变电站之间的线路的长度较长，且线路上流过的电流较大，所以变电站与“源负荷点”之间的网架的各项成本都远高于各负荷点分区内网架的各项成本。

将本方法获得的主网架规划方案记为方案1，将文献[15]中方法获得的含聚类中心的主网架规划方案记为方案2，方案2的线路走向及连接关系见附图B2。两方案的各项成本对比见表3，方案2的各项成本见附表A3。

表3 两方案的各项成本对比Table 3 Cost comparison of the two schemes 万元/年

由表3可知方案1的各项成本均低于方案2，分别降低了80.885万元/年和23.834万元/年，综合总成本降低了104.719万元/年，方案1的经济性优于方案2。分析其原因：由于变电站与等效电源点之间的网架的各项成本远大于各负荷点分区内网架的各项成本，而方案1将各负荷点分区内离变电站最近的负荷点作为“源负荷点”的方法有效缩短了变电站与各负荷点分区的等效电源点之间的线路的长度，所以网架的各项成本均更小；且方案1中各负荷点分区之间的负荷分布更加均匀，也有助于减小网架的年运行成本，故本方法获得的方案的整体经济性更好。

5.3 联络线规划方案

为降低问题的求解难度，本文在进行联络线规划时作以下简化：当某条支路发生故障时仅有该条支路被停运隔离；每次仅有一条支路发生故障；故障处理期间允许各支路以80%的负载率运行；在完成主网架规划的基础上仅在各负荷点分区之间设置联络线，而不考虑在各负荷点分区内部设置联络线的情况。

求解由式(13)—(16)确定的联络线规划模型得到联络线沿街道分布的规划方案，含联络线的网架连接关系见附图B3，含联络线的网架沿街道分布的规划方案见图3，方案的各项成本见表4。

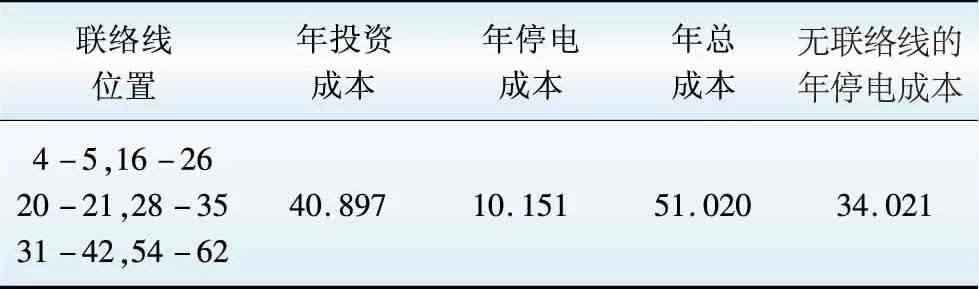
表4 联络线规划方案的各项成本Table 4 Cost of tie line planning 万元/年

由表4可知，设置联络线之后由支路故障导致的年停电成本明显降低，仅为无联络线时年停电成本的29.84%，方案的可靠性明显提高；且联络线的年投资成本与无联络线时的年停电成本相比只增加了6.876万元，故联络线的设置对提高系统的可靠性具有重要的实用价值。

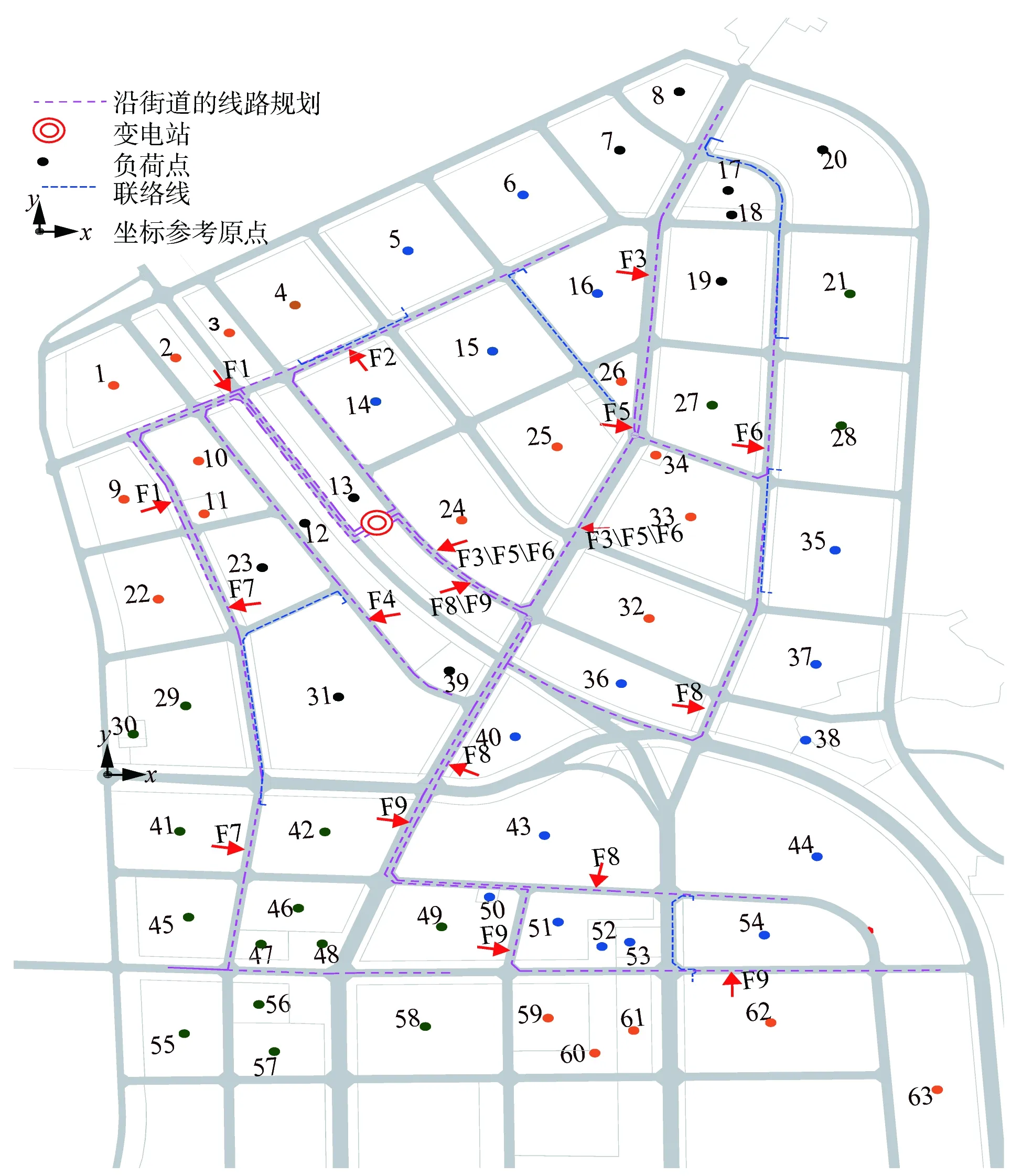
图3 含联络线的网架沿街道分布的规划方案Fig.3 Network planning with tie lines along street

6 结 论

(1)提出用负荷权重对K-means聚类算法进行改进，有效避免了因负荷分布不均造成的不同负荷点分区之间的负荷相差较大的情况，且先进行负荷点分区，再进行网架规划的方法能有效减少模型的决策变量个数，降低规划难度，提高求解效率。

(2)根据系统功率流向建立的能表示网络中负荷点上下游关系的连接关系矩阵，有助于快速计算支路电流和快速判断联络线位置对故障支路下游负荷供电恢复的影响。

(3)各负荷点分区之间的联络线规划进一步提高了网架规划方案的可靠性，并且针对不同的负荷转供情况采取了不同的停电成本计算方法，使总体规划方案更加经济合理。

虽然本方法在进行网架规划时考虑了一定的负荷裕度，但是对不确定性因素考虑得还不够深入。所以，下一步将对计及不确定性因素的网架规划模型和方法展开深入研究，以提高网架规划方案对未来不确定性场景的适应性。