基于BP神经网络的共享单车优化调度问题
◆朱 雁 马庄宣通讯作者 王诗语 温宗良,2
基于BP神经网络的共享单车优化调度问题
◆朱 雁1马庄宣1通讯作者王诗语1温宗良1,2
(1.徐州医科大学 江苏 221004;2.广西中医药大学 广西 530001)
本文根据中国优选法统筹法与经济数学研究会为2017年第七届MathorCup大学生数学建模挑战赛提供的共享单车数据,使用BP神经网络进行需求预测,从供需关系角度出发分析共享单车供需缺口。在此基础上,基于动态规划建立SSE动态时间序列模型,并通过Lingo软件求解,得到了各区域共享单车最优的调度方案。
共享单车;调度;BP神经网络;时间序列
0 引言
共享单车是指企业在居民区、商业区等公共服务区提供的单车共享服务,是一种分时租赁模式[1]。共享单车较好地解决了“最后一公里”的骑行难题,且符合绿色出行理念,正受到越来越多的关注。共享单车一般都有GPS定位,可实时监测车辆位置、骑行分布等数据,利用这些数据可对单车进行全天候供需预测。我们通过分析共享单车的使用现状,发现共享单车的供需关系并不均衡。共享单车调度是指共享单车供需不平衡时,通过相应数据的收集、整理和分析,对单车投放地址和投放数量进行调控,从而实现供需均衡。相对于国外对“有桩公共自行车”的研究,国内学者对于共享单车的研究已进入到了“无桩共享单车”的时代,但研究主要集中在发展建议、盈利模式、法律与监管等方面,对于共享单车优化调度的研究较少[2]。
我们采用中国优选法统筹法与经济数学研究会为2017年第七届MathorCup大学生数学建模挑战赛提供的共享单车数据[1]建立时空分布模型,使用BP神经网络进行需求预测,从供需关系角度出发分析共享单车供需缺口。在此基础上,基于动态规划建立SSE动态时间序列模型,并通过Lingo软件求解得到了各地区共享单车的最小投放量。
1 共享单车供需关系现状及未来供给量预测
1.1 共享单车的时空分布模型及需求预测
1.1.1数据预处理及时空分布距离分析
首先,我们对数据进行预处理。先统计出单车从i地到j地所需要的时间,取其平均值作为从i地到j地所需要的时间路程(i,j=1,2,…,10)。在某一地到其他地的时间路程已知的前提下,建立以该地区为中心的空间分布模型。然后,定义区域间邻近分布公式:若地区邻近则记为1;反之则记为0。最终,我们得出各区域时空分布距离。
1.1.2 BP神经网络模型预测分析
BP神经网络[3]又称误差反向传播神经网络,是目前应用最广泛的一种神经网络。其工作过程主要分为两个阶段:第一阶段,用一组样本训练网络,其中每一个样本都包含输入和输出。第二阶段,以输出值与样本的期望输出值进行比较。若误差未满足要求,则沿原连接通路逐层返回,并根据误差按照一定规则调整各层节点的连接权值和阈值,以逐步减小误差,直到满足要求。人工神经网络经充分训练获得了样本的特征知识,并将这些知识以权值的形式分布存储在网络的连接上。由此构成了非线性映射模型。经训练后的人工神经网络具有泛化能力,不仅对学习过的样本有效,而且对未经学习的样本也可以较准确地预测。
调取某一天各时段不同区域共享单车流量,使用1.1.1中预处理的数据,利用BP神经网络训练样本数据,然后预测一天中各时间段各区域共享单车流量,预测结果见表1所示。一天结束时,共享单车数量和为992(事先假设共享单车为1000辆),误差率为0.8%;说明该预测结果合理。
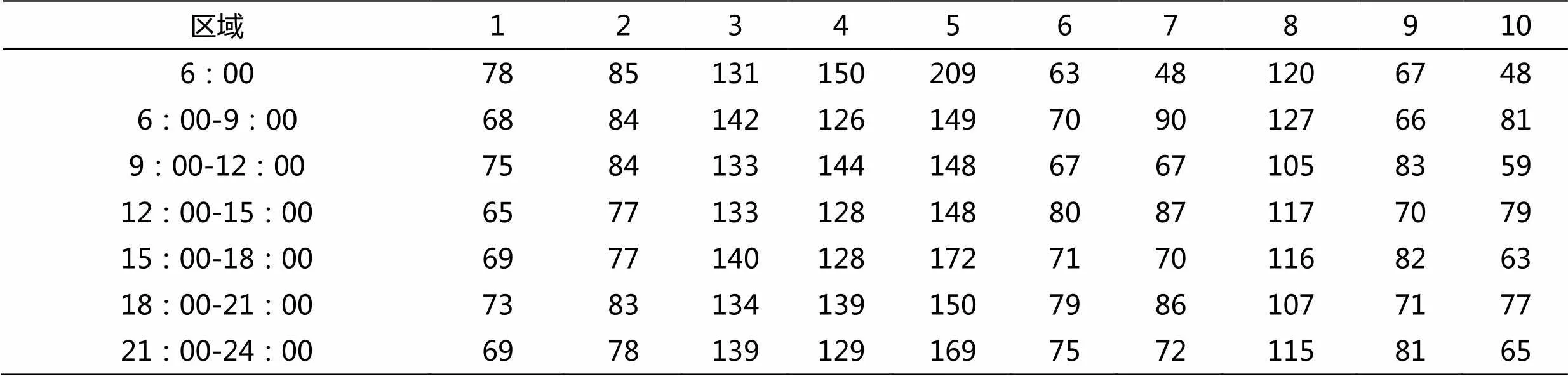
表1 时间段各地区共享单车可使用次数
1.2 各区域共享单车供需缺口比较与分析
我们对于城市内各个区域对单车的需求数据进行整理统计,得出单车投放量同需求量之间的差值,并以此差值除以单车需求量得出了需求差率这一重要指标。将需求差率运用Matlab软件进行作图处理得出所示的需求差率空间分布图(图1)和平面分布图(图2)。
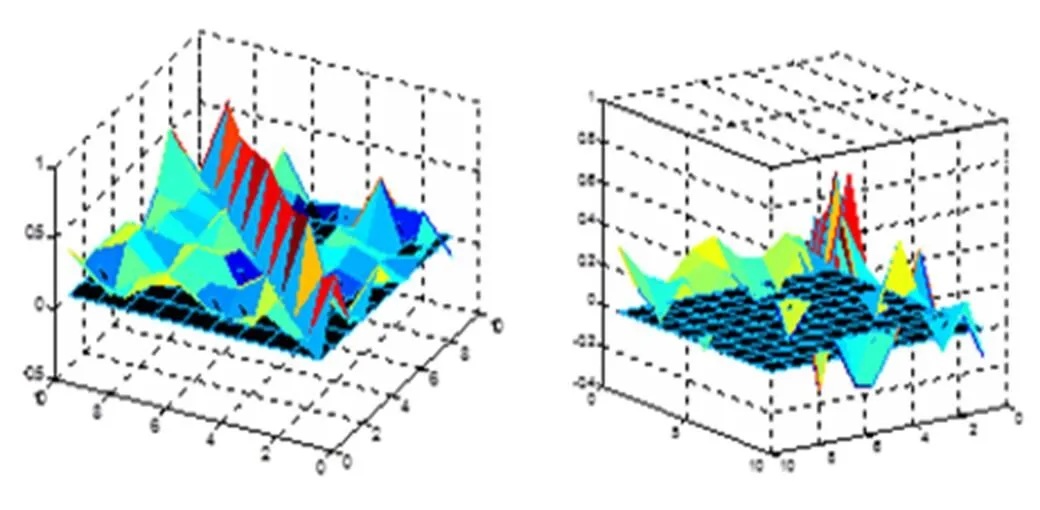
图1 需求差率空间分布图
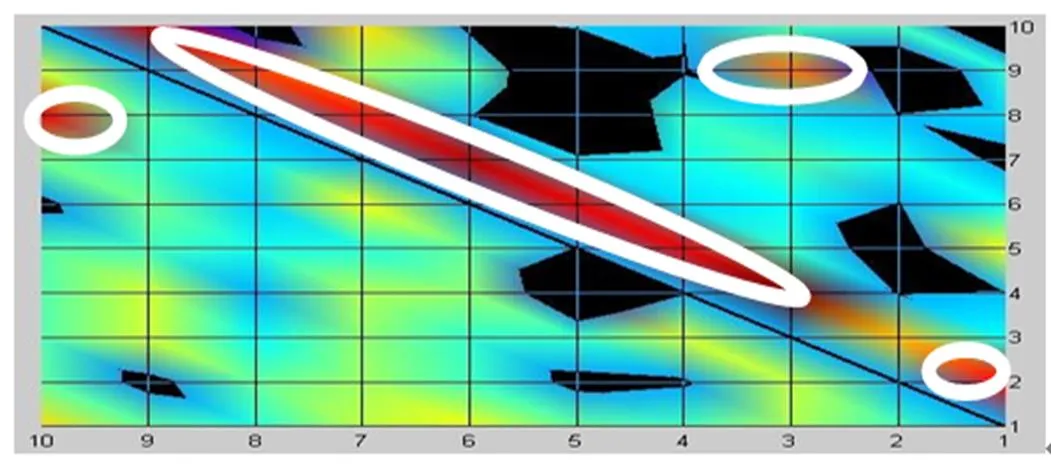
图2 需求差率平面分布图
由图1可知,图面平整度差异大,红色区域波峰较高,而某些区域波谷较低,说明整个地区共享单车分配策略存在不合理问题,选取0.2,0.4作为度量标准,大于0.2的区域对单车需求量较大,而分配量不足,说明该区域共享单车的满足程度较低;大于0.4的区域对单车需求量很大,而分配量不足,说明该区域共享单车的满足程度极低。
在图2中,红色代表满意程度极低。我们采用赋值的方法对满意度进行量化,按照空格内是否有红色区域及红色区域的数目,分别以0、1和2进行赋值来分析对单车的满意度,得出满意程度结果。10个区域中有2个得分为0,满意度“差”,6个区域得分为1,满意度“较低”,2个区域得分为2,满意度“较高”。此结果表明绝大多数区域的居民对于单车的满意程度存在较大意见,这也反映出共享单车供需关系之间的不平衡,存在较大的供给缺口,亟待优化调度。
2 共享单车优化配置方案
2.1 各区域共享单车数量增减情况调查
受市场需求及单车本身性能消耗的影响,共享单车的数量处于变化之中。我们整理得到了各区域单车增减量。如表2前四行所示。

表2 单车数量变化及优化结果
2.2 各区域共享单车最小投放量的计算
利用指数平滑法[4]描述某个区域共享单车随时间段的变化曲线,最终我们基于动态规划建立SSE动态时间序列模型[5]。由于时间序列不能进行长期预测,因此在确定最优指数平滑曲线之后,将该曲线通过的点用集合表示,然后用多项式差值对集合中的点进行拟合,建立一次多项式。通过cftool函数工具箱的差值拟合对上述模型进行曲线拟合[6],得到其自变量系数及对应的次幂。以各区域单车投放量为决策变量,根据共享单车影响因子建立非线性规划模型[7]。最后,通过lingo软件对该模型进行求解,得到各地区共享单车最小投放量(见表2最后一行)。
3 结语
随着共享单车的风靡,其配置和调度问题成为大家关注的热点。本文使用BP神经网络进行需求预测,并基于动态规划建立动态时间序列模型,得出了各区域共享单车最优的调度方案,以使系统运转更加高效。需要指出的是,本文分析所采用的数据具有一定的局限性,利用共享单车实际应用中产生的数据可更准确地进行需求预测和分析,以更好地进行车辆投放、调度和运营维护。但本文的分析方法对于共享单车的优化调度具有一定的参考价值。
[1]2017年MathorCup大学生数学建模挑战赛赛题[EB/OL].http://www.saikr.com/c/nd/5228,2017.
[2]杨证轲,董恺凌,张学梅.国内外共享单车研究综述[J]. 成都大学学报(社会科学版),2018.
[3]Simon Haykin著;叶世伟,史忠植译.神经网络原理[M].机械工业出版社,2004.
[4]叶宗斌,周步祥,林楠,黎祚,程寅.基于等维新息指数平滑法模型的中长期负荷预测[J].电力系统保护与控制,2012.
[5]董言治,刘松涛,尉志苹等.基于Matlab的时间序列分析和动态数据建模[J].计算机工程,2003.
[6]陈岚峰,杨静瑜,崔崧等.基于MATLAB的最小二乘曲线拟合仿真研究[J].沈阳师范大学学报(自然科学版),2014.
[7]Bonnans J F, Gilbert J C, Lemaréchal C, et al. Numerical optimization: theoretical and practical aspects[M]. Springer Science & Business Media,2006.
徐州医科大学课题(D2016002),广西自然科学基金项目(2018GXNSFAA138200),广西哲学社会科学规划研究课题(15FGL008),广西中医药大学课题(QN14006)。

