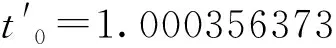时、频效应实验及数学关系式的验证
梁世铎
(温州市航海学会,浙江 温州325000)
0 引 言
根据多普勒效应[1],观测者与波源之间存在相对运动时,测者测得波源频率不等于波源发射频率;相互靠近运动时,测者测得频率高于波源发射频率;相互背离运动时,测得频率低于波源发射频率。该实验笔者在1988年就做过声波实验了。
测者A用两只电子秒表,分辩率为0.01s,一只由B拿着坐在出租车上(在温州牛山北路测速段),A站在路旁,小车以90km/h(25m/s)速度向着A方向行驶,B每隔2s说一声“按”,司机就按响喇叭,A听到喇叭声①,立即按下秒表,再一次听到喇叭声②,就按停秒表。A测下喇叭声①与喇叭声②的时间间隔。①声号与②声号不是在同一地点发射的,两者相差50m(25m/s×2s),这50m,声波需走0.14s(50m/340m/s)。小车背离A行驶与向着A行驶,测得的时间间隔t=2±0.14s(见图1)。
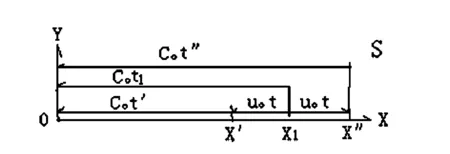
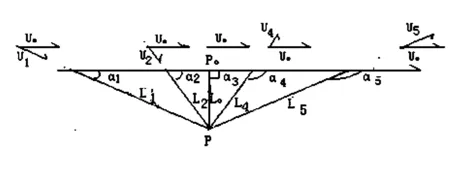
图1 声源移动与声波传播图
A在坐标S系原点O处,波源在X轴X1处,声信号①由X1传送到O点,传送距离为C0t1。在发射信号①的瞬间,向测者(或背离测者)以U0的速度运动了t时间间隔,运动了U0t的距离,至X′(X″)处的瞬间,发射了信号②,信号②由X′(X″)处传送了C0t′(C0t″)距离到达O点,由此建立式(1):
C0t′-C0t1=U0t
(t′-t1)C0=U0t
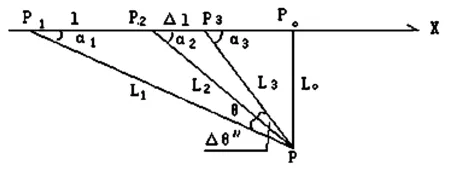
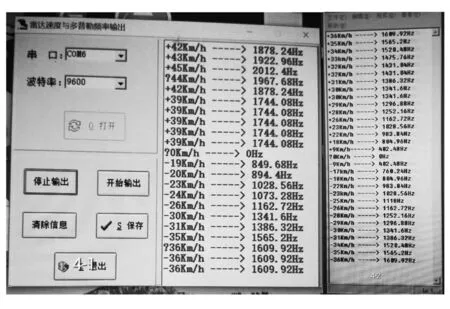
∵t′ ∴-△tC0=U0t得 -△t=tU0/C0 (1) 式(1)为波源向着测者运动的关系式。 同理:波源背离测者运动的关系式:C0t″-C0t1=U0t整理,得式(2): △t=tU0/C0 (2) 可知,小车背离测者运动了50m(或向着测者)的间隔发射了两个声号,50m声波需走0.14s,故测得结果为2s± 0.14s。 该实验是用声波声速(340m/s)做实验,如果用光波光速(299792458m/s)做实验,精度要求太高,50m光波只需1.6×10-7s,该精度一般仪器达不到要求。 2013年笔者得到欧伦福平板PSD-3型、K波(2.413209697×1010Hz)雷达测速仪,在观测中,PSD-3型与平板电脑连接,在平板电脑上有数据“雷达速度与多普勒频率输出”,有效距离100m。 f=f0(1+cosβ0u0/C0)/(1-cosα0u0/C0) (3) 式(3)中:f为观测频率;f0为发射频率;β0为测者接收运动视分量角;α0为发射源运动视分量角。雷达波往返是瞬间完成的,故接收视分量角β0与发射视分量角α0相等,即β0=α0=α,式中运动速度也相等,即u0=U0,C0为光速。 将式(3)整理得式(4): f/f0=(1+cosαU0/C0)(1+cosαU0/C0)(1-cosαU0/C0)(1+cosαU0/C0) 1+Δf/f0=1+2cosαU0/C0 得Δf=2f0cosαU0/C0 (4) 因PSD-3雷达测速仪的有效观测距离为100m,车速不可过快,以36km/h(10m/s)较为理想,这样往返100m可以测得20多个数据。 PSD-3雷达测速仪[3]观测中,小车向着测者以36km/h匀速行驶时,由式(4)可知: 当α′=0时,Δf=f02U0/C0,U0=ΔfC0/2f0 (5) 将f=2.413209697×1010Hz U0=10m/s C0=299792458m/s 代入式(4) 得:Δf=1609.92Hz 小车一路驶来,车速保持36km/h匀速,而雷达测速仪所测数据是变化的,如图2所示。 图2 雷达测速视分量角变化图 当:α1=30°.558,U1=31km/h,Δf1=1386.32Hz; α2=60°,U2=18km/h,Δf2=804.86Hz; α3=90°,U3=0,Δf3=0; α4=120°,U4=-18km/h,Δf4=-804.96Hz; α5=149.442°,U5=-31km/h,Δf5=-1386.32Hz; α″=π,U″=-36km/h,Δf=-1609.92Hz。 由图2可见,随着小车(匀速直行)相对测者的运动视分量角是变化的,由式(4)知,雷达测速仪所测出的数据也不同,多普勒频率Δf是接收频率f与发射频率f0之差(Δf=f-f)。一般的雷达测速仪将接收返射雷达波f与雷达本振雷达波f0混频,将多普勒频率Δf再由式(5)计算而得小车行驶视速率U,而PSD-3雷达测速仪将多普勒频率Δf数据也显示出来,见图3。 图3 PSD-3雷达测速仪在平板电脑上所得数据 由于路上车辆多,很难得到理想的数据。图3中的数据是在温州市瓯江七都岛屿北面沿江边道上而测,该道路平直,没有来往车辆,小车保持时速36km,按图2的示样,往返200m行驶,测得多组数据,图3为其中一组,较为理想,“+”为向着测者行驶,“-”为背离测者行驶。 在此,首先对图3数据组进行验证,见表1。 表1 对雷达测速仪数据验证 由以上系列计算的数字与图3中数据的验证;式(3)、(4)可行,经得起实验的验证。得出以下结论: (1)P0为蓝移(靠近测者)和红移(背离测者)的临界点,蓝移过程,视速率在渐渐变慢,至临界点时,视速率为零(与车辆真速度快慢无关),过临界点后,红移视速率渐渐变快。 (2)观测过程,视分量角都在渐渐变大(0→π)。 (3)观测频率在渐渐变低(观测周期在渐渐变慢,作者的8位数微波观测仪有效距离能达100m,就可直观周期在观测中,只会在渐渐变慢),与频率源向着测者或背离测者无关。 (4)匀速直线运动的发射源,在蓝移区与红移区以临界点为基点,视分量角和视速率两边对称。 1916年由美国天文学家巴纳德(Edward Emerson Barnard,1875-1923)发现,自行为每年10.3角秒,所有恒星中年自行值最大的飞行之星“巴纳德星”。 笔者现知两个数据;SIMBAD是106.8km/s与ARIONS是110.8km/s,而且观测视速率向太阳系靠近,年自行值为10.31角秒,知道巴纳德星在蓝移区,向临界点P0靠近,而自行值在变大(对于同等的矢量,离临界点越近,其张角越大)。 设:1916年,巴纳德星视速率U1为110.8km/s,年自行值Δθ′为10.3角秒,视分量角为α1, 2017年视速率U2为106.8km/s,年自行值Δθ″为10.31角秒,视分量角为α2。由1916年至2017年总计101年自行总量为θ=(0°0′10.3″+0°0′10.31″)101/2=0°17′20.81″。 图4 蓝移区示意图 设巴纳德星真速率为U0,U0=U1/cosα1,U0=U2/cosα2=U2/cos(α1+θ) 得U1/cosα1=U2/cosα1cosθ-sinα1sinθ 整理:U2/U1=(cosα1cosθ-sinα1sinθ)/cosα1 U2/U1=cosθ-tgα1sinθ 得tgα1=(cosθ-U2/U1)/sinθ (6) 将:U1=110.8,U2=106.8,θ=0°17′20.81″代入式(6), 得tgα1=7.15191873,α1=82°2′25.29″ 巴纳德星真速率: U0=U1/cosα1=800.1413348km/s,α2=α1+θ=82°19′46.1″ 巴纳德星真速率: U0=U2/cosα2=800.1413372km/s 在图4中的X轴P1点上,有两艘飞船①、②,同一瞬间从P1出发。①飞船向P点以光速飞行,经过t1时间间隔到达P点,在P点等候,②飞船先沿X轴向P2点以U0速率飞行,经过t0时间间隔到达P2点,即刻转向P点,以光速飞行,经过t2时间间隔到达P点,此瞬间而①飞船在P点已等侯了t时间间隔。 ①飞船用时t1+t,②飞船用时t0+t2,①飞船与②飞船在同一瞬间从P1点出发,又到达同一点P,只是①飞船早到了t时刻,两飞船用时相等,得t1+t=t0+t2 (7) C0t1=L1 C0t2=L2 从图4中知: ∵L1≠L2 ∴t1≠t2t≠t0,将地球时转换成巴纳德星时。将式(3)变换为: t=t0(1-cosαU0/C0)(1+cosβU0/C0) (8) 因地球天文台观测所有星空天体的自行与视速率,都是以太阳系为参照,故(8)式中U0=0,(8)式成为: t0=t/(1-cosα0U/C) (9) 巴纳德星现年自行值Δθ″=10.31″,将α3=α2+Δθ″=82°19′56.41″、U0、C0、Δt代入式(9),得:t0″=1.000356241年。 取t0′、t0″平均值Δt0=1.000356307年,地球1年时,巴纳德星而为1.000356307年时。 将图4中Δ1计算出距离,Δ1=Δt0×U0/C0=2.669934978×10-3光年。 在△PP2P3中:Δ1/sinΔθ″=L3/sinα2=L2/sin(180-α3) L3=Δ1·sinα2/sinΔθ″=52.93751987光年,t3=52.93751987年。 L2=Δ1·sinα3/sinΔθ″=52.93787618光年,t2=52.93787618年。 由式(7)同理知, t2+Δt=Δt0+t3 t2+Δt=53.93787618年 Δt0+t3=53.93787618年 由以上数据得知式(7)正确。 在△PP1P2中:L1/sin(1800-α2)=L2/sinα1, L1=L2·sinα2/sinα1=52.97471293光年,t1=52.97471293年。 将t1=52.9747293年,t=101年,t2=52.93787618年代入式(7),得: t0=t1+t-t2=101.0368368年,由地球时101年求知巴纳德星101.0368368年。 式(6)不但满足蓝移区,也能满足红移区,过蓝红移临界点后进入红移区,视速率渐渐变大。仍以巴纳德星为例,将:U1=106.8km/s,U2=110.8km/s,θ=0°17′20.81″,代入式(6),得: tgα1=-7.424921349,α1=-82°19′46.1″=180-82°19′46.1″=97°40′13.9″,真速率U0=U1/cosα1=-800.1413372km/s α2=α1+θ=-82°2′25.29″=180-82°2′25.29″=97°57′34.71″ ,真速率U0=U2/cosα2=-800.1413348km/s。 式(6)能满足视速率为蓝移的天体,也满足视速率为红移的天体。可以先对太阳系临近的而视速率存在变化的天体进行测算,求知真速率、真距离。随着时间的推移,渐测求知远离太阳系的天体,将对宇宙有一新认识。1 频率效应式[2]
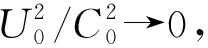

2 巴纳德星[4]