火力发电厂干灰库温度应力及裂缝计算方法
王学民
(中国能源建设集团浙江省电力设计院有限公司,浙江 杭州 310012)
1 概 述
钢筋混凝土筒仓在我国许多行业有广泛使用,如粮食、水泥、煤炭行业,其贮料物种的特性与其它行业有所不同。贮灰库在火力发电厂中得到了广泛的应用。在电厂中,灰渣是在锅炉排出后通过输灰管道直接送到储灰仓内,温度可达100 ℃左右,而外部温度随季节和地区不同,差别较大。在北方地区的冬季,室外气温可达-30 ℃,灰库内外温差近130 ℃。即使在南方的夏季,灰库内外的温差也近50~60 ℃。温度作用对混凝土的强度和弹性模量均有影响,引起混凝土变形增大,收缩和徐变加剧;同时,钢筋在受热状态下受力性能、粘结性能和变形性能也将发生变化。
较大的温差会对灰库结构产生较大温度应力和温度变形,而现行的《混凝土结构设计规范(GB 50010—2003)》[1]中虽然考虑了温差对筒仓结构作用,但仅考虑了常温贮料下外界气温变化温差引起的温度作用,不能解决电厂贮灰库存在的温度问题。对于温度作用下的筒仓设计,虽然已作了一些研究[2-3],但是没有一种针对电厂干灰库比较适用的设计方法。
目前,电厂干灰库设计中对温度问题的考虑主要有以下几种办法:内部设计隔热内衬、外部设计保温层、通过温度计算加大配筋,但对于筒壁温度作用的考虑没有提出明确的方法。
2 温度作用下的材料性能
现行《钢筋混凝土筒仓设计规范(GB 50077—2003》中规定了温度作用下的混凝土和钢筋的力学性能,见表1~4。
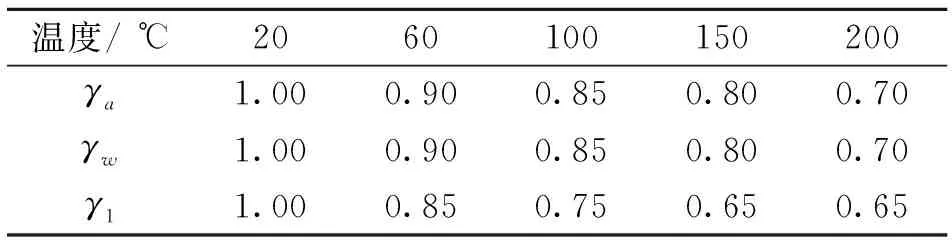
表1 温度作用下的混凝土强度折减系数
注:γa、γw、γ1分别为温度作用下混凝土轴心抗压、抗弯压或弯拉及抗裂设计强度折减系数。

表2 温度作用下的混凝土弹性模量折减系数
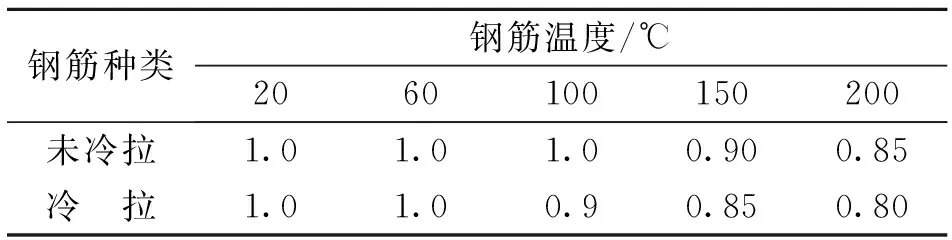
表3 温度作用下的钢筋强度折减系数

表4 温度作用下的钢筋弹性模量折减系数
3 温度作用
筒壁任意点的受热温度计算,可按平壁法计算。假定热流按稳定条件下传热,材料假定为匀质体,即随时间变化,内部气体温度及热流大小是常数,根据热量平衡条件可以推导出温度计算公式。气体传热考虑的主要是对流传热,而灰库内是高温散料,散料与筒壁间的热传导包括对流、辐射和导热,三种传热方式同时存在,所以,灰库的温度计算方式不能套用内部为气体时的温度计算方法,否则会产生较大误差。
当仓内干灰料位较低时,干灰处于流化态,此时可采用简单的平壁法计算仓壁内外温差。
在满仓时,干灰为非流化态,可参考文献[2]的做法,取靠近筒壁且其厚度等于筒壁厚的散料作为隔热层,按平壁结构的稳定热传导原理,计算筒壁内表面温度。具体方法如下:
(1)
式(1)中:Tcj为计算点的受热温度(℃);
Tn为库内散料最高温度(℃);
Tw为库外空气温度(℃);
Rz为内衬、筒壁、隔热层等总热阻(m2·K/W);
Ri为第i层热阻(m2·K/W)。
4 温度应力计算
由弹性力学分析可知,两端自由的无限长圆筒在温度作用下的应力为:
(2)
(3)
式(2,3)中:a为筒壁内径;
b为筒壁外径。
弹性力学的分析假定内外温差沿筒壁呈线性变化,而且考虑的是同一种材料。对于钢筋混凝土筒壁,学者所关心的是钢筋与混凝土之间的应力差,所以,不能直接应用弹性力学公式。
对于温度作用下钢筋混凝土筒壁钢筋和混凝土的应力计算,可采用如下假定[4]:
1)截面应变符合平截面假定;
2)温度单独作用下压区应力图形呈三角形;
3)受拉区混凝土不参与工作;
4)计算混凝土压应力时,不考虑界面开裂后钢筋的应变不均匀系数和混凝土应变不均匀系数。在计算钢筋的拉应力时,考虑钢筋的应变不均匀系数,但不考虑混凝土应变不均匀系数;
5)筒壁能自由伸缩但不能自由转动,因此温度应力只需计算由筒壁内外表面温差引起的弯曲约束下的应力值;
6)计算方法为分别计算温度作用和荷载标准值作用下的应力值后进行叠加,在叠加时要考虑荷载标准值作用下的混凝土压应力及钢筋拉应力的降低。
由此,可得出筒壁温度应力计算公式:
(4)
(5)
(6)
(7)
εt为筒壁内表面与外侧钢筋的相对自由变形值;
εt=1.25(αcTc-αsTs);
αc、αs为混凝土、钢筋的线膨胀系数;
Tc、Ts为筒壁内表面受热温度和外侧钢筋受热温度;
fttk为混凝土在温度作用下的抗拉强度标准值。
5 裂缝计算
现行《钢筋混凝土筒仓设计规范(GB 50077—2003)》规定,裂缝按现行《混凝土结构设计规范》(GB 50010—2002)计算,其中的最大裂缝宽度计算公式为:
(8)
式(8)中各符号的意义参考混凝土规范。
该公式未考虑温度作用。在温度作用下,灰库混凝土抗拉强度降低,钢筋和混凝土的粘结性能退化,容易产生裂缝。当筒壁内热外冷时,内壁面呈压应力,外壁面的纵向及环向均呈拉应力。当最大应力超过抗拉强度时,外表面将出现裂缝。一般纵向裂缝常见,而环向裂缝少见。
要考虑温度作用,最简单的办法就是对该公式进行修正。考虑灰库的工作特性,作以下两点修正:
1)对公式中的受拉钢筋应力,代之以温度与荷载共同作用下的受拉钢筋应力;
2)考虑在长期高温作用下,钢筋与混凝土之间的粘结强度有所降低且滑移增大的影响,应增加一个大于1的工作条件系数k。
考虑温度作用的最大裂缝宽度计算公式:
(9)
(10)
(11)
式(9~11)中:
σskt为荷载标准值和温度共同作用下裂缝处钢筋应力;
αcr为构件受力特征系数;
k为工作条件系数;
ni为第i种钢筋根数;
ρte为以有效受拉混凝土面积计算的受拉钢筋配筋率;
di、deq为第i种受拉钢筋及等效钢筋直径(mm);
c为混凝土保护层厚度(mm);
νi为受拉钢筋的相对粘结特性系数。
6 算例分析
某电厂干灰库,内径15 m,储灰温度80 ℃, 储灰高度19 m,储灰密度14 kN/m3,冬季室外最低气温-5.8 ℃。筒壁配筋均以HRB335级钢筋直径25 mm间距150 mm考虑,筒壁厚度考虑400 mm和300 mm两种情况,同时考虑设与不设120 mm厚耐火砖。导热系数取值见表5,混凝土筒壁为1.74+0.000 5T;耐火砖内衬为1.1+0.000 5T;干灰为1.2。计算时工作条件系数取1.0。
采用本文的方法,计算出各种情况下的结果如表5~6所示。
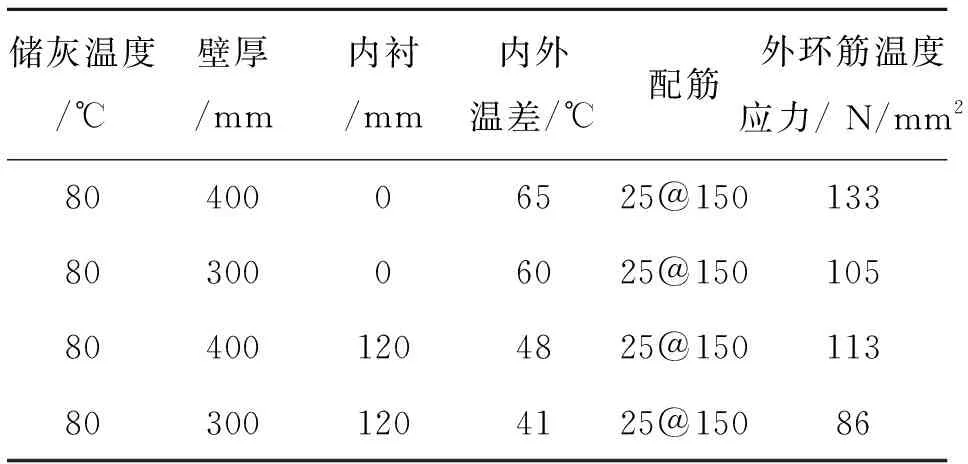
表5 储灰料位较低,流化态时的计算结果

表6 储灰满仓时的计算结果
由计算结果可见,温度对干灰库的影响不容忽视。
7 结 语
通过本文的分析可以得出如下几条结论:
1)温度作用对电厂干灰库的影响不容忽视;
2)弹性力学的温度应力计算公式不能直接用于灰库分析,可以采用烟囱规范的方法,但是相对比较繁琐;
3)可以将文中裂缝计算公式用于灰库分析,但是其工作条件系数有待于进一步研究。

