基于MATLAB的某型压气机试验数据处理分析
文信,刘超
(中国航发湖南动力机械研究所中小型航空发动机叶轮机械湖南省重点实验室,湖南株洲,412002)
0 引言
本文以航空发动机重要部件之一——压气机的折合流量和出口温度为例,基于MATLAB的数据拟合快速地从一系列采样数据中逼近待测函数或曲线,然后通过编程指令建立它们之间的简单回归方程,对某一特定参数进行预测,为评估压气机性能提供了理论基础。
1 一元线性回归
1.1 a,b估计
回归分析是研究相关关系的一种重要的数学工具,它能通过对客观事物中变量的大量观察或试验获得的数据,去寻找隐藏在背后的相关关系,然后给出它们的表达形式——回归函数,即可从一个变量取得的值去估计另一个变量的值。
一般地,设x与y之间存在某种相关关系,表示为:
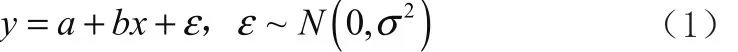
其中a,b及σ2都是不依赖于x的未知参数。ε为随机误差且σ2未知。(1)式称为一元线性回归模型,由两部分组成,一部分是回归直线a +b x(a,b是回归系数),另一部分是不可控的随机误差 ε~ N (0 , σ2) 。
对于(x,y)的样本( x1,y1),(x2,y2),…, (xi,yi)有:
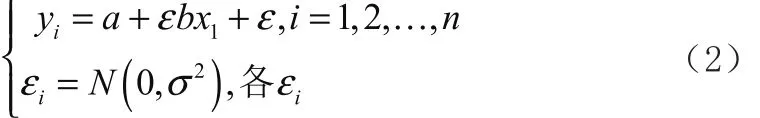
由样本得到(1)式中回归系数的估计a和b,称y=a+bx为经验回归直线。用最小二乘法来估计模型(1)的未知参数a和b,考虑a、b的函数:
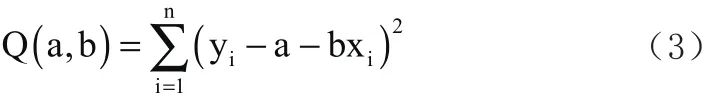
称 Q ( a,b)为偏差平方和。最小二乘法就是选择a和b的估计aˆ和bˆ,使得Q( a,b)为最小,即:

方程组有唯一解:
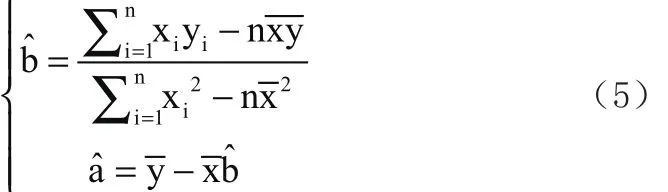
在线性假设y =a+b x+ ε 的前提下, 用最小二乘法得到了经验回归方程:

1.2 残差ε估计
在进行回归方程的显著性检验之后,还不能保证数据拟合得很好,也不能排除由于意外原因而导致数据不完全可靠,比如有异常值出现、周期性因素干扰等。只有与模型中的残差项有关的假定满足时,才能放心地运用回归模型。因此,在利用回归方程作分析和预测之前,应该根据残差图判断回归效果与样本数据的质量,检查模型是否满足基本假定,以便对模型作进一步的修改。
1.3 线性假设的显著性检验
在实际工作中,事先并不能判定y与x确有关系。前面得到的回归模型只是一种假设。当然,这个假设不是没有根据,可以通过专业知识和散点图做出粗略判断。但求得的线性回归方程是否具有实用价值,一般来说,需要经过假设检验才能确定。本文的检验过程放在如表1所示的方差分析表中进行。具体的计算结果可以通过调用MATLAB程序得到。
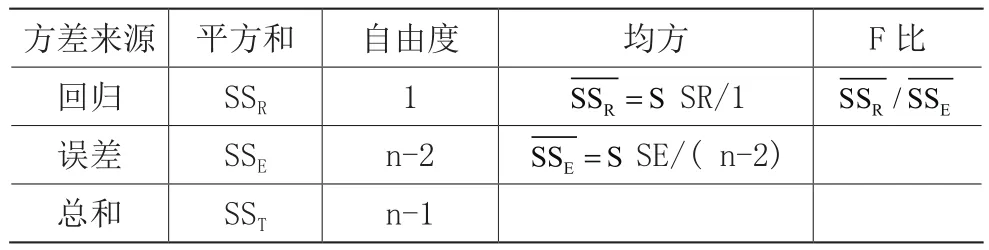
表1 方差分析表
对于显著性水平∂的选取,视具体情况而定,通常取 ∂=0.01和 ∂=0.05,从 F分 布表上查出 F0.01(1 , n−2)和F0.05(1 , n−2)。如果F > F0.01(1,n −2 ),说明回归方程高度显著,如果 F>F0.05(1 , n− 2 ),说明回归方程为显著。如果F < F0.05(1 , n −2 ),说明回归方程不显著。
1.4 点预测和区间预测
经验回归函数的一个重要应用是可利用它对因变量进行点预测和区间预测。
当回归模型确定后, 可由给定的 x0,预测y0的值,预测值(点估计),这就是线性回归的点预测。
假设区间预测的置信因子为(∂通常∂=0.05),利用经验公式得到y0的置信水平为1-∂的置信区间为:
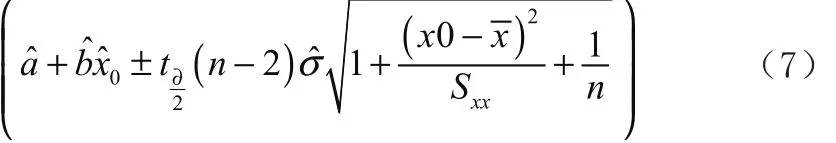
其中:
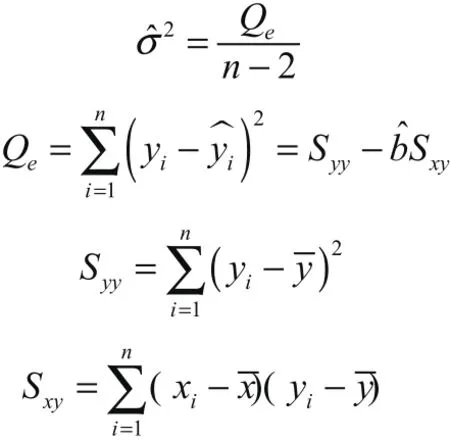
2 试验数据处理、分析及验证
以某型压气机折合流量和出口温度的试验数据为例,通过数据分析和处理,寻求两者之间的关系。首先对数据进行预处理分析,剔除压气机冷吹时的数据点,并找到折合转速为0.2到1.0时折合流量和出口温度的数据,剔除粗大误差点,作如图1所示的散点图(文中所有折合流量的单位是kg/s,出口温度的单位是℃)。
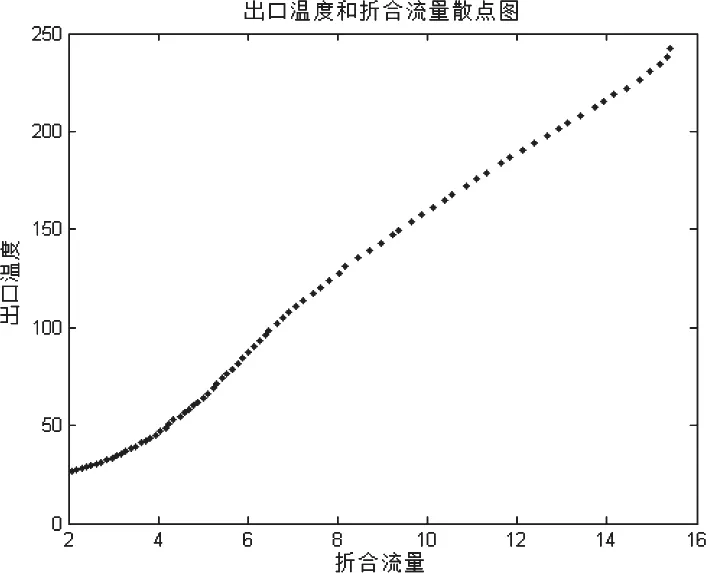
图1 折合流量和出口温度散点图
2.1 数据的回归模型
在MATLAB窗口调用编写的程序得到五个数值b、bint、R、rint、stats。其中b是回归系数;bint是回归系数的区间估计;R是残差;rint是置信区间;stats是用于检验回归模型的统计量,有4个数值:(a)相关系数(相关系数越接近于1,回归方程越显著);(b)F统计量观测值;(c)F统计的概率P值(当P小于显著性水平时,说明拟合模型有效);(d)误差方差的估计。
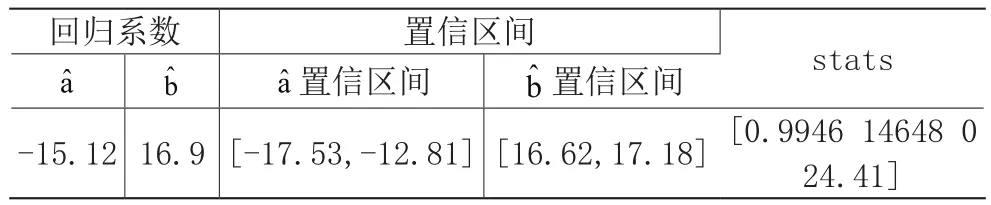
表2 回归模型相关参数表
回归模型求出后,需要方差分析,进行显著性检验,具体计算结果如表3所示。

表3 试验数据的方差分析表
由表2和表3的结果可得出以下几个结论:
(1)stats(1)=0.9946,接 近 于1,说明回 归模型高度显著;(2)当显著性水平为0.01或者0.05时,stats( 3 ) = 0<0 .01( 0.05),因此回归模型y=−15.12 +1 6.9x有效;(3)F比为14647.84,该值远大于 F0.01(1 , 79)和 F0.05(1 , 79),说明回归模型高度显著。
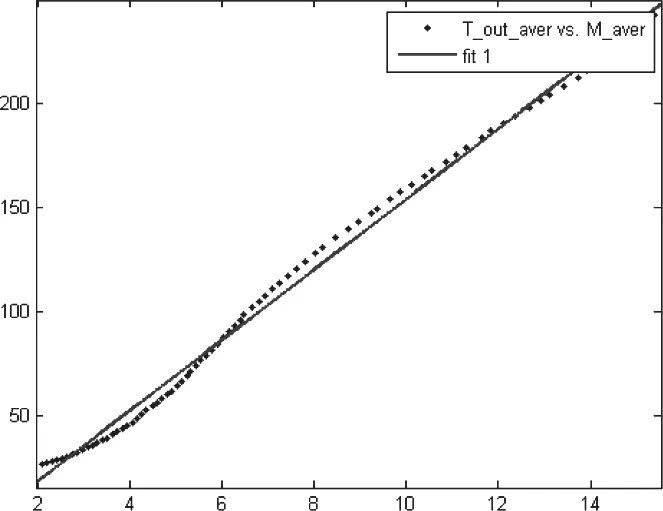
图2 折合流量和出口温度拟合曲线图
根据计算出的一元回归方程可以画出图2中的拟合曲线图。
在MATLAB命令窗口中输入rcoplot(R,rint)命令,得到残差分布图如图3所示。
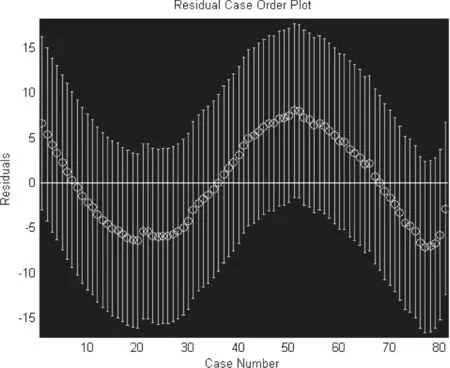
图3 残差分布图
由残差分布图可知,各个点的置信区间均包含零点,说明没有异常数据且回归模型能较好的符合原始数据。
2.2 验证回归模型
在相同工况、装配状态下,将第一次试验数据作为训练集求出回归模型;将第二次试验数据作为测试集,用于检验回归模型的准确性。
画出第二次试验数据的散点图,如图4所示。
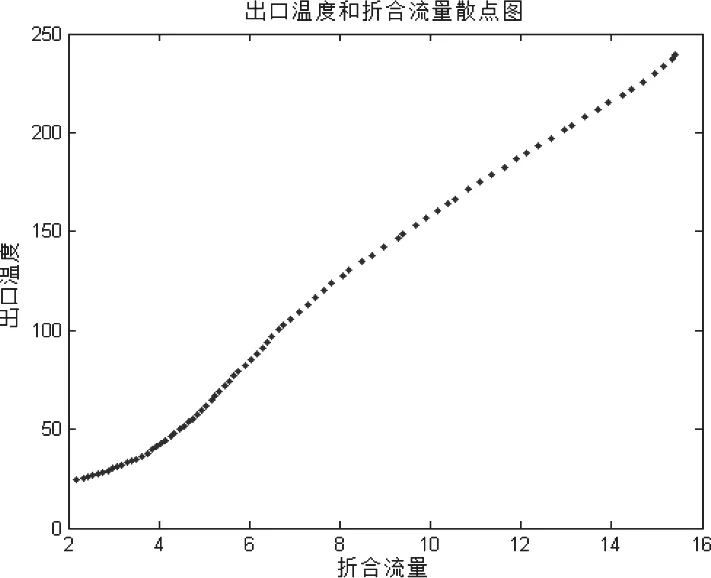
图4 验证数据的折合流量和出口温度散点图

表4 测试数据的方差分析表
由计算结果可知,F比为9079,该值远大于 F0.01(1 , 79)和F0.05(1 , 79),说明回归模型对于测试集数据仍然适用。因此只要在压气机试验状态不改变的情况下,在每次试验推转速的过程中便可以利用该回归模型提前预测压气机出口温度。
2.3 利用回归模型进行预测
假设在试验时知道折合流量为10.14376,给定置信因子0.05,就可以利用回归模型即经验公式对出口温度进行预测。当折合流量为10.14376,压气机出口温度的估计值为:
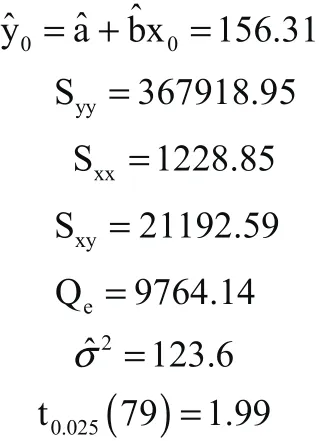
利用经验公式和公式(7)得到0ˆy的置信水平为0.95的置信区间为:()156.3122.32±,即(133.99,178.63)。而出口温度的实际值为160.29,在这个区间之内。由此证明预测是正确的。但如果工作中出现实际值不在置信区间的情况,也不能马上否定预测,首先检查车台的温度受感器是否有故障,然后再对预测做出判断,例如放气活门漏气也会引起压气机出口温度升高。
3 结论
本文借助MATLAB建立了折合流量和出口温度的线性回归模型,并根据散点图初步判断它们之间存在线性关系,通过F检验证明该回归模型高度显著。然后对数据进行残差分析,在没有异常数据的基础上,利用所得的经验公式对折合流量和压气机出口温度进行预测,为判断试验状态是否正常提供了理论基础,从而大大提高了试车的效率和安全性,极具必要性。

