飞行器三自由度制导控制仿真及应用

王宝和，赵志敏

(中国人民解放军91550部队， 辽宁 大连 116023)

飞行仿真广泛应用在飞行器论证、研制、试验、鉴定、作战使用等各阶段，主要分为三自由度仿真、六自由度仿真。其中，六自由度仿真技术比较成熟[1-3]，仿真精度更高，能够满足制导姿控系统设计验证和试验鉴定的需求，但在飞行仿真过程中需要准确掌握系统制导姿控方程和相关仿真模型参数[4]，为飞行器的飞行仿真工作带来了很大的困难。三自由度仿真技术由于运行速度快，基于少量的输入参数即可开展仿真等特点，一般应用在对仿真精度要求不太高的情况下，也经常应用在飞行器论证设计和作战使用技术研究领域[5-6]。

本文为了降低飞行仿真对模型参数的依赖，通过假设条件和近似处理，将六自由度模型简化为三自由度模型，基于少量的、必要的诸元参数，实现飞行器三自由度飞行仿真。为了更贴近飞行器飞行工作过程，尽可能不影响仿真精度，本文采用分段建模的方式，将整个轨迹划分为多个飞行段落，各时序事件均按标准判据触发，避免了部分研究中采用按时间触发的现象，使计算结果更逼近真实结果。结合仿真实例探索了不同纬度、不同射向发射对射程的影响，为飞行器的使用提供帮助。

1 飞行器控制原理

飞行器控制系统主要由制导系统、姿控系统及时序控制系统等组成，系统工作原理具体见图 1所示。其中需要由地面装订的诸元包括制导诸元、姿控诸元、时序判据诸元、制导工具误差系数诸元、发射诸元等，涉及参数百余项。

制导系统的主要功能是利用平台测量的视加速度进行导航计算，提供飞行器实时位置和速度参数，对质心运动进行控制，按照制导律使飞行器从某一飞行状态达到要求状态的轨道机动，并达到期望的终端条件以保证命中目标。具体功能为：

1) 惯性平台实时测量飞行器的视加速度；

2) 进行实时导航计算，计算飞行器运动参数；

3) 按一定的制导律进行导引控制和关机控制；

4) 进行惯性平台工具误差实时补偿。

姿控系统的主要功能是控制和稳定飞行器的绕心运动，在各种初始条件及干扰作用下确保飞行器按预定弹道稳定飞行，使姿态角偏差在允许的范围之内。

姿控系统接受两个方面的信息，一是来自姿态敏感器的信息，这个信息是由于飞行器受干扰作用使姿态偏离原来状态而产生的。姿态敏感器信息经过自动稳定装置生成控制信号，再通过伺服机构产生控制力，控制力作用于箭体，使箭体回到原来姿态位置，这样形成一个负反馈的自动稳定闭环系统，保证箭的姿态稳定。另一控制信息来自制导系统，它们是弹道程序转弯的程序角指令和导引指令，这些指令要求姿态保持，使之通过姿态控制达到调整质心运动轨迹的作用。

时序控制系统主要功能是监测时序判据参数，判断各时序发生时刻，并控制完成相应时序动作。不同时序的控制方案也不尽相同，有发动机压力控制方案、时间备保方案、加速度表控制方案、行程控制方案、姿态角控制方案等。重要的时序在设计上存在冗余，即有两种或两种以上不同类型的控制方案。

2 三自由度弹道建模

由飞行器控制原理分析可知，若要采用精度较高的六自由度仿真，必须掌握百余项诸元参数，为飞行器仿真提出了较大的难题。所以，在对仿真精度要求不太高的前提下，通过简化六自由度模型，建立了三自由度模型，在只需要发动机推力及秒耗量、飞行程序角、空气动力系数、时序判据诸元等参数条件即可完成仿真。

计算假设条件[6]：

1) 飞行器近似为刚体，仅考虑其在铅垂面内的运动，发动机推力矢量始终沿着弹体轴向，不考虑主发动机喷管产生的控制力及其力矩的作用；

2) 飞行器绕质心的转动满足瞬时平衡要求。即飞行器转动至俯仰程序角的动态过程瞬间完成，始终处于作用力矩平衡的状态。

2.1 三自由度弹道模型

通过简化飞行器六自由度方程[7-9]，在发射坐标系内建立飞行器三自由度运动方程，见式(1)。

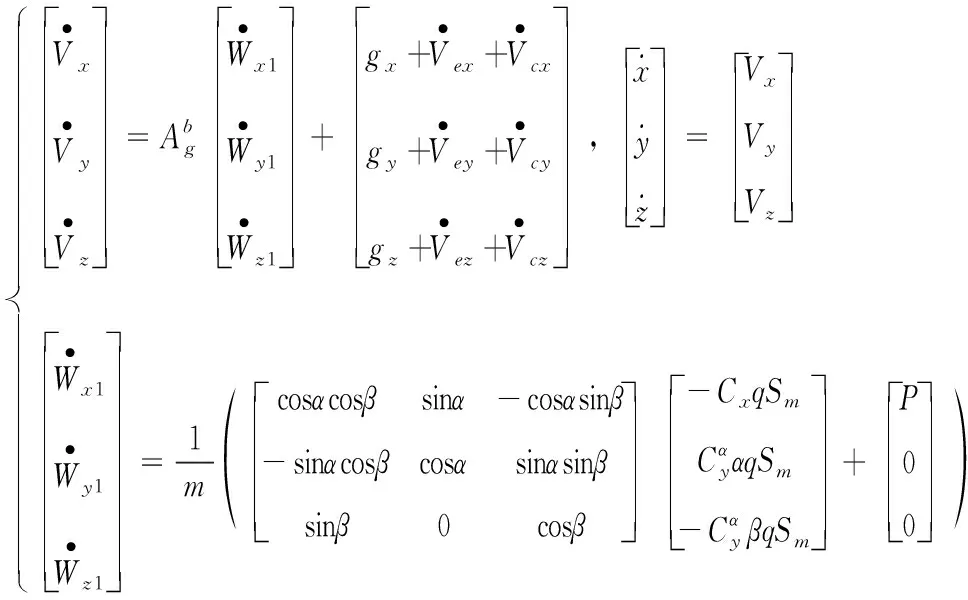
(1)

(2)

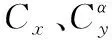
飞行器的倾角θ、偏角σ、攻角α和侧滑角β计算式为：

(3)

2.2 弹道分段

飞行器在飞行过程中，由于受到的外力和剩余质量在不断变化，各飞行段的若干参数和制导方法也会发生阶段性改变。上述动态变化因素为弹道建模带来一定难度，在建模过程中，需要通过合理划分飞行弹道段落，降低计算的复杂程度[10]。

根据飞行器从起飞到落地过程中的受力情况和飞行特点，可将飞行弹道分为主动段、自由段和再入段，见图2所示。根据发动机的工作状态，主动段又可以细分为一级飞行段、二级飞行段、三级飞行段。根据主发动机、滚控发动机和伺服机构的工作情况，一级飞行段又可分为一级前过渡段、一级基本段、一级后过渡段；二级飞行段又可分为二级前过渡段、二级基本段、二级后过渡段；三级飞行段又可分为三级前过渡段、三级基本段。

2.3 时序实时控制

在飞行器飞行仿真过程中，飞行时序控制的准确与否，直接影响到外力作用的段落以及剩余质量的大小，最终影响仿真的精度。部分高校和研究机构在弹道理论研究中，时序控制通常采用按时间触发的方式，即飞行器飞行至装订时间触发相应的时序。但在飞行器实际飞行过程中，时序控制判据更加复杂，不同时序的主副判据也不尽相同，包括时间、视加速度、发动机燃烧室压力、冲量等判据。为此，在飞行仿真中，需要根据真实时序判据进行实时控制，并考虑时序指令持续时间，确保在不同发射工况、飞行环境和飞行器自身偏差下的仿真与实际飞行过程尽可能保持一致。

3 仿真计算及实例分析

本研究基于Matlab语言建立了飞行器三自由度仿真软件，具体计算流程见图3所示，发动机推力及秒耗量、飞行程序角、空气动力系数等诸元参数采用真实数据，大气参数采用标准大气参数[11]，射程仿真计算结果与实际试验相比误差在1 500 m内，表明三自由度弹道模型正确，计算结果可信。

基于最大标准射程为5 000 km的飞行器虚拟模型，开展仿真算例计算，发射点纬度分别取北纬0°、30°、60°和90°，不同射向对实际射程的影响见图4(a)～图4(d)。由计算结果可知，该型飞行器在赤道上向东发射实际射程可达5 514 km，向西发射实际射程可达4 620 km；在北纬60°线上向东发射实际射程可达5 240 km，向西发射实际射程可达4 796 km；在北极点全向发射实际射程均在5 000 km左右。由仿真结果可总结出如下规律：① 在同一纬度向东发射实际射程要大于标准射程，向西发射实际射程要小于标准射程；② 高纬度发射增程/减程效应要小于低纬度，在北极点发射时，射向对射程没有影响。

基于最大标准射程为5 000 km的飞行器虚拟模型，开展仿真算例计算，发射射向间隔取30°，研究相同射向发射时，纬度对实际射程的影响，结果如图5(a)、图5(b)所示。

由计算结果可知，在不同的发射纬度， 60°和120°射向的射程基本一致，在30°纬度射程为5 382 km，在60°纬度射程为5 209 km；240°和300°射向的射程基本一致，在30°纬度射程为4 715 km，在60°纬度射程为4 826 km。由图可总结出如下规律：① 向东发射时发射点纬度越高实际射程相对越近,向西发射时发射点纬度越高实际射程相对越远；② 90°射向对应射程最远，270°射向对应射程最近；③ 以东西向为轴，对称角度的射程基本一致，如60°与120°射程基本一致，210°与330°射程基本一致。

通过对最大标准射程为5 000 km、6 000 km和7 000 km飞行器仿真计算，箭体各子级结构质量每增重1 kg对最大标准射程的影响见表1。从表1中可以看出，不同射程的飞行器，各级结构质量的影响也不一致，最大标准射程越远，相同的结构质量影响越大；增加相同结构质量，三子级比二子级和一子级对标准射程影响大。

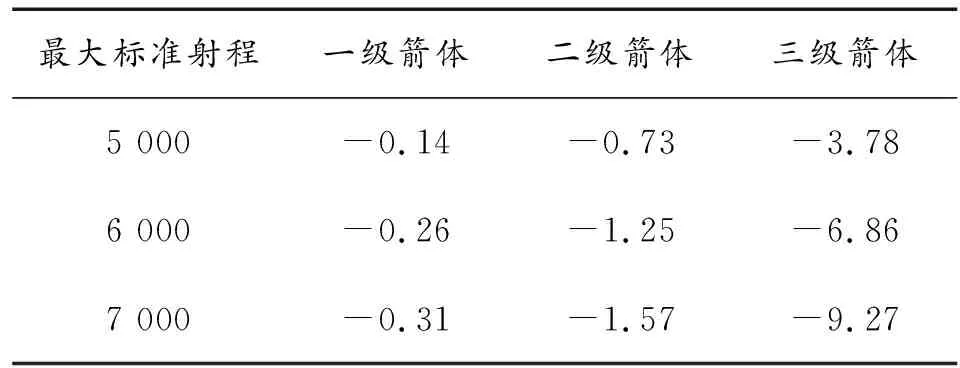
表1 结构质量每增重1 kg对最大标准射程的影响统计表 km

4 结论

根据飞行器飞行弹道控制特点，基于弹道分段和时序实时控制技术，建立了飞行器三自由度弹道模型。结合具体算例，仿真计算飞行器不同纬度、不同射向、不同结构质量发射对射程的影响，为飞行器发射点选取和实际使用提供了理论支撑。