P波初至到时自动拾取技术研究

王俊 杨驰 詹小艳 朱峰 张金川 钱婷

摘要：基于粘滞性单自由度振动器响应下的能量转换理论，提出利用阻尼能量作为目标函数的P波震相到时拾取方法-SDOF Picker算法。使用该方法对江苏及邻区2010-2016年实际记录的9607组P波初至进行到时自动拾取测试，以地震编目中人工拾取到时为基准，与利用AIC算法自动抬取的结果进行了系统性对比分析，结果显示：SDOF Picker算法和AIC算法自动拾取P波初至的准确率分别为97.1%、91.8%，中值偏差分别为（0.02±0.61）s、（0.05±0.77）s，方差分别为0.37s2、0.60s2，这表明SDOF Picker算法的在准确率和拾取精度方面均优于AIC算法。

关键词：粘滞性单自由度振动器；阻尼能量；P波初至到时；AIC算法；SDOF picker算法

中图分类号：P315.3 文献标识码：A 文章编号：1000-0666（2018）01-0038-08

0 引言

地震定位、震源机制求解及地震动预测等许多地震学应用中，P波到时的精确拾取均十分关键。目前，地震台网通常采用半自动处理方法，即通过数值算法拾取一个大致位置，再由分析人员进行复核、修正。这是因为一般情况下人工拾取的精度更高，尤其是在信噪比较低时，但人工拾取震相到时存在主观性且费时。未来随着地震台站规模不断增大，特别是在地震早期预警与地震动预测中，从海量连续记录波形数据中自动、精准地拾取震相到时的需求将愈加迫切。

1980年以来，出现了许多检测与拾取不同地震波到时的方法，大多是通过寻找地震信号与背景噪声（或长时平均振动）之间能量、极化特征以及频谱成分的变化特征来进行的（杨配新等，2004；王彩霞等，2013）。通常情况下，地震信号在某一特定的频带范围内会被强化或沿一定的方向极化（Lomax et al，2012），大多数检测方法通常还会对记录信号进行去除线性趋势、滤波等预处理，以期降低背景噪声或提高信号强度。在众多P波到时检测方法中，STA/LTA方法的应用最为普遍（Allen，1978；Earle，Shearer，1994）。该方法是以对比信号短时平均/长时平均特征为基础，通常将随时间的绝对值或均方根作为特征函数，当STA/LTA超过预设或设定的动态触发阈值时，视为有效检测。该方法对检测振幅的变化非常有效，但它的精度依赖于设定的检测间隔与阈值；另外与地震信号无关的脉冲型噪声，尤其叠加在微震记录中时会引起误触发检测。

自回归（AR）方法也常角来检测震相。这类方法是假设地震波能被分解为部分稳态的多个过程，每个模型作为一个AR处理，初至前、后被视为2种具有不同性质的状态（Sleeman，Van Eek，1999； Rastin et al，2013）。为检测到理想的触发时间，需要分离初至前（信号中仅包含背景噪声）与初至后（信号中包含地震波和背景噪声）特征，使用AR技术分析不同窗内的时间信号。例如，一般的背景噪声通过相对低阶的AR就可以很好地表征，而地震信号则通常需要高阶的AR才能较好地表征（Leonard，Kennett，1999）。采用AR分析处理时序信号时，赤池信息准则（AIC）能帮助确定AR处理的阶数，这就意味着模型匹配同样存在不确定性（Akaike，1974）。AR-AIC是另一种常用的有效方法（Leonard，2000；赵大鹏等，2012），但当时间窗内存在多重震相时，AIC捡拾器则会拾取振幅最大的震相，另外，它不能辨别时间窗内的信号是真正的震相到时，还是由传感器故障或数字噪声引起的干扰信号（Kalkan，Stephens，2017）。除此之外，神经网络方法（Dai，MacBeth，1995）、小波变换（高静怀等，1997；Anant，Dowla，1997；刘希强等，2000）、滑动互相关能量比（Forghani-Arani et al，2013）等方法也被用来拾取震相到时，但这些方法都有一个共性，即需要一个或多个经验性预设，如检测间隔、阈值设定、事件特征、信号的频谱成分等。

本文基于粘滞性单自由度（简称SDOF）振动器响应下的能量转换理论，提出利用阻尼能量作为目标函数的P波震相到时拾取方法——SDOF Pick-er算法。再利用2010-2016年江苏省地震台网记录到的9607条P波波形进行详细测试，并分析了拾取精度。

1 基本原理

在粘滞性单自由度振动系统响应下，由记录信号传递给振动器的输入能量会被转换为弹性应变能，随后由阻尼元件产生阻尼能量进行耗散，阻尼力与速度成正比（欧朱光，2003）。图1给出典型粘滞阻尼单自由度振荡器的示意图。

这2个振动器的运动方程，可以用一个普通二阶微分方程来表示：

mut+cu+ku=0（1）式中：m为质量；c是阻尼系数；k是刚度系数；ut是质量块的绝对（总）位移，且ut=u+ug，ug是地面运动位移，u是质量块相对于底座（如地面）的相对位移。式（1）可以写为：

mu+cu+ku=-mug（2）式（2）的右边是与地动加速度（ug）有关的激发函数。对式（1）、（2）中u进行积分将得到2种不同定义的输入能量。对式（1）中的u进行积分，给出了线弹性粘滞阻尼SDOF振荡器运动（图1a）的绝对（总）能量公式，其遭受的运动加速度（ug）可以表示为：式中：t代表时间。式（3）还能写成更一般的表达式，用能量来表示：

Ek+Eζ+ES=EI（4）式中：Ek是绝对动能；Eζ是阻尼能量；ES是弹性应变能。这些项相加就等于传递给SDOF振荡器的能量，即绝对输入能量EI。

对式（2）进行积分，可得出基准固定情况下（图1b）线弹性粘滞阻尼SDOF振荡器的相对能量公式：式（5）可写成：

Ek'+Eζ+ES=EI'（6）式中：Ek'是相對动能；EI'是相对输入能量。式（4）中的EI表示外力（mut）在质量块上的作用已经完成，相当于总基底-剪切力对地面运动位移上的功已经完成。另一方面，式（6）中的EI'代表等效侧力在基准固定情况下振荡器的功已完成，从而去除了刚体转换效应。2个能量公式之间EI'和EI的差异导致了2个动能Ek'和Ek之间的差异，然而，阻尼能量和应变能量项在这两种定义中均被保留。在粘滞性阻尼SDOF振荡器中，单位重量的阻尼能量耗散的功率，通过对Eζ进行时间的微分，可表示为：式中：ωD是角频率；ζ是阻尼比，用2π/TD来表示；TD是阻尼振动的固有周期，与无阻尼振动的固有周期（Tn）相关，可表示为：

2 P波初至到时拾取算法

在地震波激励情况下，能量的变化可采用底座固定状态下线弹性粘滞阻尼SDOF振动器（图1b）的相对能量公式来表述。在时域里，由式（2）可得到质量块的相对速度u。在u已知的情况下，利用式（5）便可计算出不同的能量值。由式（5）和式（7）可知，阻尼能量是累积的函数，且正比于质量块的相对速度，这使得阻尼能量是一个随时间变化的光滑包络线函数，在记录开始至P波到达之前接近于零（或平坦），P波到达后迅速增大（Erol，2016），本文提出的方法便是利用阻尼能量的平滑特性來进行P波初至到时的检测，简称为SDOF Picker算法。由于背景噪声与地震波信号之间具有不同的频率分布特征，因此阻尼能量函数在信号开始时即会发生显著变化，于是可将其作为跟踪并检测P波初至到时的有效度量。固有周期小的振动器，由于不会产生延迟和震相以外的响应，因此对于这种变化具有更高的敏感性。

在P波初至到时的拾取中为防止共振，将SD-OF振动器的固有周期设置为0.01s，因此具有相对较高的谐振频率，该频率高于地震波信号中大部分频率；阻尼比取值为0.6，这类似于短周期地震计。在0.6的阻尼水平或更高的状态下，频率响应接近于巴特沃斯（Butterworth）滤波器所能保留的最大的平坦幅度和相位角响应，这意味着输入信号的频谱能完整地被传递到振荡器的响应中。在这样的固有周期和阻尼比状态下，振荡器能迅速回到平衡位置，且没有自由振荡也不影响输入能量特性。图2是2017年2月24日江苏金湖ML1.5地震宝应台垂直分向的记录波形及各能量计算结果，震中距约为11.7km，从图中看到，相对输入能量是相对动能（图2c）、弹性应变能量（图2d）、阻尼能量（图2e）的总和，大部分作为应变能被保留和释放，随后由阻尼器进行能量耗散，振动器的动能可忽略不计，因为质量块相对于基准位置几乎没有运动。最后，通过检测阻尼能量功率（图2f）来进行震相到时拾取。

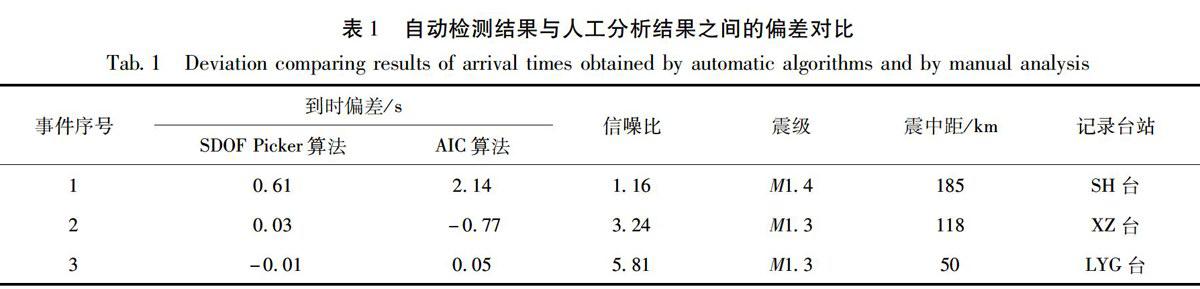
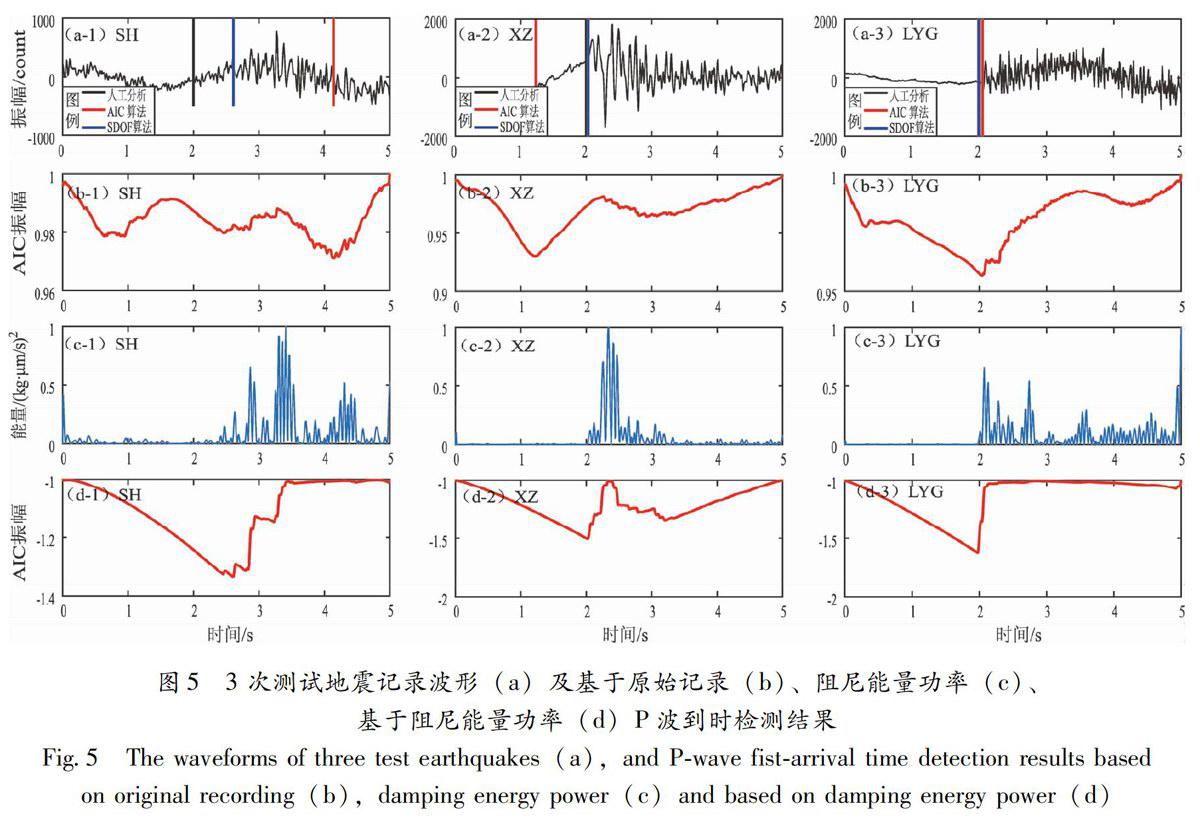
为验证SDOF Picker算法的拾取精度，本文将其与AIC算法、人工拾取的结果进行对比分析。图3是2017年江苏金湖ML1.5地震宝应台三分向记录的检测结果，记录波形采样率为100Hz，记录中BHE分向的噪声水平显著高于其它2个分向，这3种方法拾取的P波到时位置用不同颜色的竖直线进行标注（图3a）。在这次地震中SDOF Picker算法在BHZ，BHE、BHN三分向上的捡拾结果与人工拾取结果之间偏差分别仅为0.01s，0.02s，0.01s，与AIC算法的拾取结果之间偏差则分别为0.02s、2.83s、0.02s；从图3中可看出，尽管AIC算法在BHZ、BHN分向上的检测结果与人工分析结果也十分接近，但在具有高噪声干扰的BHE分向上，AIC算法则未正确拾取出P波到时，拾取出的位置为S波震相到时。为更进一步检验SDOF Picker算法在低信噪比下的拾取性能，定义信噪比为人工初至拾取震相到时前、后各1s的振幅平方之比（Hildyard et al，2008），图5给出了P波段信噪比分别为1.16、3.24、5.81时江苏泗洪台（SH）、徐州台（XZ）及连云港台（LYG）垂直向记录的检测实例，其中SH台、XZ台的仪器频带范围为60s～50Hz，LYG台的仪器频带范围为120s～50Hz，记录采样率均为100Hz，到时偏差对比结果见表1。

从表1中的3组实测结果看，随着信噪比的提高，2种算法的结果与人工分析结果之间的偏差均逐渐减小，但SDOF Picker算法的检测结果与人工分析结果之间偏差更小，意味着即使是在信噪比极低的情况下，阻尼能量的功率也能精准地反映出背景噪声与地震波信号之间的差异特征，而从基于原始记录波形的AIC曲线结果可以看出（图5a-2、b-2），在低信噪比下的宽频带记录中容易受到记录中长周期固有信号的“误导”，致使震相到时拾取偏差较大。

3 系统性测试

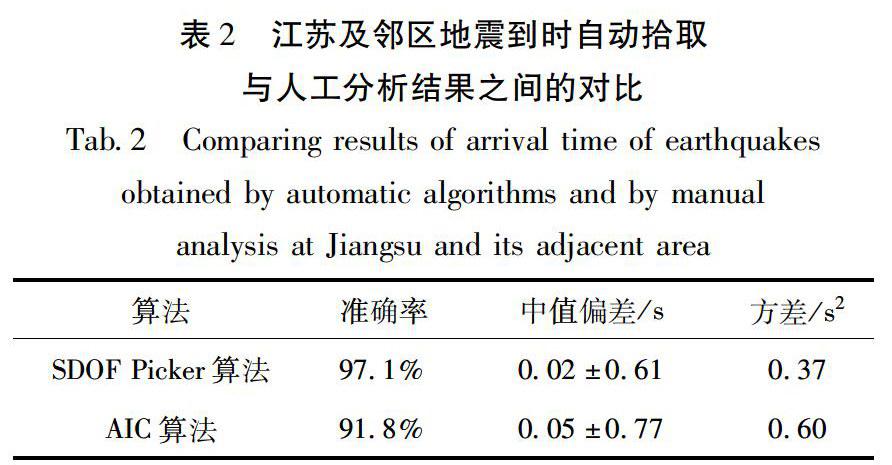
为更系统地测试SDOF Picker算法的可靠性，本文对2010-2016年江苏及邻区1444次M0.1～4.9地震（图6），选取其中震中距小于200km地震的9607个P波初至到时进行自动拾取，以江苏省测震台网人工正式编目结果中的P波到时为基准，将自动拾取到时与人工到时之间偏差大于2s的结果视为误拾取，2种自动算法拾取结果的准确率与精度对比见表2。

从表2的9607组自动拾取结果中可以看到，相比于AIC算法，SDOF Picker算法拾取的准确率提高了5.3%，中值偏差减小了0.03s，方差减小了0.23s2，中值偏差和方差的减小意昧着与人工分析结果之间系统性偏差更小，自动拾取精度优于AIC算法；从绝对偏差统计分布结果中可以清晰地看到，SDOF Picker算法拾取结果的正态分布特征也更加显著（图7）。根据到时偏差与信噪比之间的统计结果（图8）：在AIC算法自动检测结果中，与人工分析结果相比到时偏差小于0.5s的比例约为总样本数的56.5%，而在SDOF Picker算法的自动拾取结果中，这一比例则高达76.7，相对于AIC算法拾取效率提高了20.2%。当信噪比范围设定在较低的1～5时，震相样本数为4 015组，此时AIC算法自动拾取结果中偏差小于0.5s比例约占样本数的38.9%，而在SDOF Picker算法的结果中这一比例则高达65.8%，相对于AIC算法拾取效率提高的幅度更大，约为26.9%。这表明SDOF Picker算法拾取性能更优，尤其是在低信噪比下能正确拾取出的弱信号更多，拾取效率更高。

4 结论

本文基于粘滞性单自由度振动器响应下的能量转换理论，提出利用阻尼能量作为目标函数的P波初至拾取算法SDOF Picker算法。该算法将记录信号转换到粘滞性单自由度振动器响应下，由于阻尼能量函数是与时间相关的光滑一包络线函数，在P震相到达时会迅速增大可以清晰地拾取出来，因此相比于传统的检测方法，如STA/LTA等，SDOFPicker算法不需要指定任何检测间隔或设定触发阈值，也不需要对记录台站的背景噪声或被检测事件等进行先验研究，因此便于广泛地进行实际应用转化。利用2010-2016年期间江苏地震台网实际记录的9607组P波初至测试了其性能，测试结果显示：SDOF Picker算法拾取的准确率和精度整体均优于AIG算法，特别是在低信噪比记录情况下，其拾取效率更高。

自動识别和检测震相对于地震早期预警和快速处理主震之后的大量余震非常关键，因此本文所描述的检测算法对于高精度自动拾取P波初至到时具有实际意义。目前，SDOF Picker算法已经在江苏省地震台网进行实际应用，主要用于系统性自动识别前震时间窗和基于自动拾取的P波初至到时进行地震定位。未来还将在此理论基础上进一步研究S波震相到时的自动拾取技术。

参考文献：

高静怀，汪文秉，朱光明，等.1997.小波变换与信号瞬时特征分析[J].地球物理学报，40（6）；821-832.

刘希强，周蕙兰，沈萍，等.2000门用于三分向记录震相识别的小波变换方法[J].地震学报，22（2）：125-131.

欧朱光.2003.工程振动[M].武汉：武汉大学出版社，17-55.

王彩霞，白超英，王馨.2013.地震震相初至自动检测技术综述[J].地球物理学进展，28（5）：2363-2375.

杨配新，邓存华，刘希强，等.2004.数字化地震记录震相自动识别的方法研究[J].地震研究，27（4）308-313.

赵大鹏，刘希强，李红，等.2012.峰度和AIC方法在区域地震事件和直达P波初动自动识别方面的应用[J].地震研究，35（2）；220-225.

Akaike H.1974.A new look at the statistical model identification[J]Trans Automat Contr，19（6）：716-723.

Allen R V.1978.Automatic earthquake recognition and timing from singletraces[J].Bull Seismol Soc Am，68（5）：1521-1532.

Anant K S，Dowla F U.1997.Wavelet transform methods for phase identi-fication in three-component seismograms[J].Bull Seismol SocAm，87（6）：1598-1612.

Dai H，MacBeth C.1995.Automatic picking of seismic arrivals in localearthquake data using an artificial neural network[J].Geophys JInt，120（3）：758-774.

Earle P，Shearer P.1994.Characterization of global seismograms using anautomatic picking algorithm[J].Bull Seismol Soc Am，84（2）：366-376.

Erol K.2016.An Automatic P-Phase Arrival-Time Picker[J].BullSeismol Soc Am，106（3）：1-16.

Forghani-Arani F，Behura J，Haines S S，et al.2013.Anautomated cross-correlation based event detection technique and its application to asurface passive data set[J].Geophys Prospect，71（4）：778-787.

Hildyard M W，Nippress S E，Rietbrock A.2008.Event detection andphase picking using a time-domain estimate of predominate periodTpd[J].Bull Seismol Soc Am，98（6）：3025-3032.

Kalkan E，Stephens C.2017.Systematic Comparisons Between PRISMVersion 1.0.0，BAP，and CSMIP Ground-Motion Processing[R].U S Geol Surv Open-File Rept.

Leonard M，Kennett B L N.1999.Multi-component autoregressive tech-niques for the analysis of seismograms[J].Phys Earth Planet In，113，247-263.

Leonard M.2000.Comparison of manual and automatic onset time picking[J].Bull Seismol Soc Am，90（6）：1384-1390.

Lomax A，Satriano C，Vassallo M.2012.Automatic picker developmentsand optimization；Filter Picker-A robust，broadband picker for real-time seismic monitoring and earthquake early warning[J].SeismolRes Lett，83（3）：531-540.

Rastin S J，Unsworth C P，BenitesR，et al.2013.Using real and syntheticwaveforms of the Matata swarm to assess the performance of NewZealand GeoNet phase pickers[J].Bull Seismol Soc Am，103（4）：2173-2187.

Sleeman R，Van Eck T.1999.Robust automatic P-phase picking；An on-line implementation in the analysis of broadband seismogram re-cordings[J].Phys Earth Planet In，113（1-4）：265-275.