降低螺旋锥齿轮接触应力及传递误差方法的研究

黄艺鸿，聂晓根，黄文通

(福州大学 机械工程及自动化学院，福建 福州 350108)

0 引言

螺旋锥齿轮具有较大重合度、传动效率高、承载能力强、传动平稳等优点广泛应用于飞机、机床等领域[1-3]。在实际生产应用中分析螺旋锥齿轮的啮合状态，计算其接触应力及其传递误差，一直是螺旋锥齿轮的研究前沿问题。Simon[4]研究了安装误差和齿形误差对螺旋接触轨迹的影响；汪中厚[5]等人通过导入假想共轭齿面进行了螺旋锥齿轮齿面接触分析，并通过有限元分析螺旋锥齿轮的传动误差；汪中厚等人[6]还采用张量分析的方法，对螺旋锥齿轮的齿面接触分析及基于五轴联动数控机床的全齿面综合优化设计加工方法进行了深入研究；王鹏[7]等人基于啮合原理分析了国内外螺旋锥齿轮研究进展。然而，由于螺旋锥齿轮的几何特性和啮合原理导致其啮合过程中接触应力及传递误差不易控制。

为了改善螺旋锥齿轮啮合接触质量，降低啮合过程中的接触应力及传递误差，本文以端面滚刀加工螺旋锥齿轮为研究对象，建立齿面接触方程，分析加工过程中降低齿面接触应力及传递误差的方法，为后续螺旋锥齿轮的研究提供了一定的理论参考。

1 螺旋锥齿轮齿面方程的建立

在该研究过程中采用假想齿轮的方法来解释端面滚刀范成法加工过程中产生的螺旋锥齿轮及其齿面方程。该假想齿轮是虚拟齿轮，其轮齿是由刀盘切削刃轨迹形成的；螺旋锥齿轮齿面的形成运动实质上就是将连续的刀具切削面方程从刀盘坐标系Ke(xe、ye、ze)根据啮合原理和齐次坐标变换转换到假想平顶齿轮坐标系Kc(xc、yc、zc)下，即可得到齿面方程。根据图1采用变换可由式(1)表示：

(1)

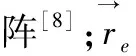
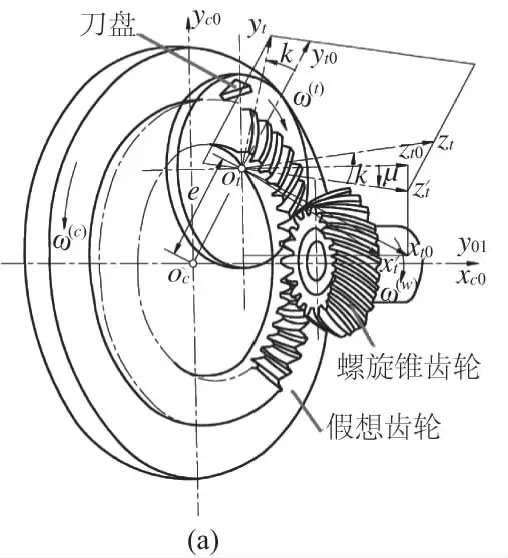
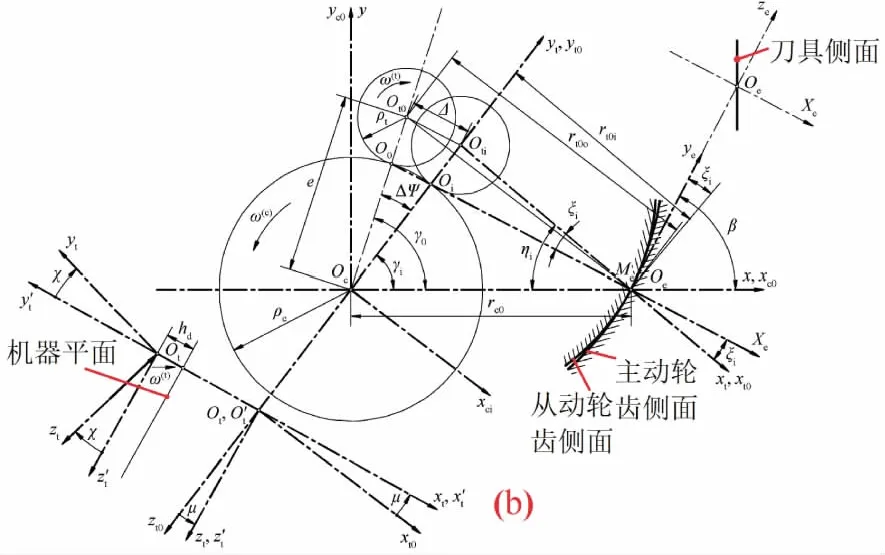
图1 螺旋锥齿轮

图1中，κ为刀具倾角；μ刀具旋转角；ρc为假想齿轮的节圆半径；ρt为刀盘半径；γi为刀盘轴初始角度；ζi为刀具偏移角；hd为刀具距离机器平面的倾斜距离；e为机床径向设置距离；ω(c)、ω(t)分别为假想齿轮、刀盘的角速度。

为了获得加工过程中螺旋锥齿轮齿面方程，假设螺旋锥齿轮和平顶齿轮共轭啮合，如图2所示。图2为假想平顶齿轮与螺旋锥齿轮的坐标系，Kc(xc、yc、zc)表示假想平顶齿轮坐标系，K1(x1、y1、z1)、K2(x2、y2、z2)分别表示齿轮1、齿轮2的坐标系。图2中的ω(1)、ω(2)分别为齿轮1、齿轮2的角速度；Φ1、Φ2分别为齿轮1、2啮合过程中的转角。齿轮1、齿轮2齿面方程由式(2)—式(3)定义：

(2)

(3)

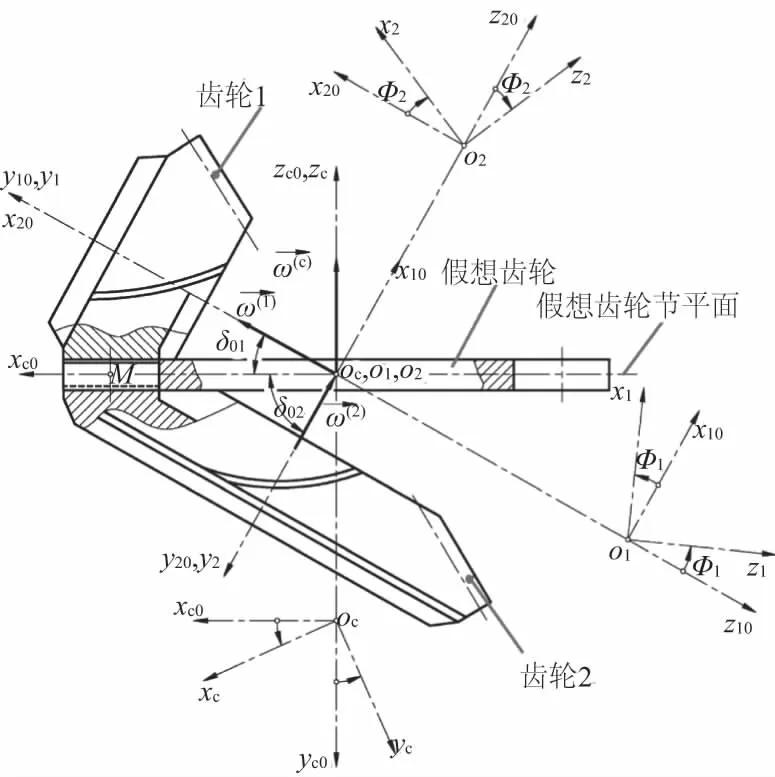
图2 坐标系

2 最大接触应力及传递误差计算

2.1 齿面载荷分布分析

在相同载荷条件下，基于螺旋锥齿轮安装角度位置误差、轮齿的瞬时接触线计算齿面载荷分布；计算过程中将齿面接触点的复合位移作为轮齿变形，同时考虑轮齿间的分离、错位及复合齿形误差。因此，瞬时接触线应满足式(4)：

(4)

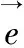
任意接触点D处轮齿表面法向方向上的复合位移Δyn可由式(5)表示：

Δyn=w(zD)+s(zD)+en(zD)

(5)

式中：zD为点D沿着接触线方向的坐标；w(zD)为点D处的总变形量；s(zD)为点D出的齿面相对分离；en(zD)为点D处的复合误差，该误差为大小齿轮的制造装配误差总和。

点D处的总变形量定义为：

(6)

式中：Lit为齿轮副it处接触线的几何长度；Kd(zD,zF)为影响系数，Kd包含大小齿轮轮齿弯曲和剪切变形，大小齿轮弯曲、扭转以及支撑轴变形。Kc(zD)为大小齿轮轮齿接触间的影响系数；p(zF)、p(zD)分别为在F、D处的轮齿载荷。

接触点距大小齿轮轴的距离是时刻变化的，传递力矩可定义为：

(7)

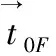
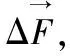
(8)

Δyn(it,iz)=w(it,iz)+s(it,iz)+en(it,iz)

(9)

(10)

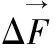
总变形量定义为：

w(it,iz)=wt(it,iz)+wc(it,iz)+wgs(it,iz)

(11)

式中：wt(it,iz)为大小齿轮轮齿复合弯曲和剪切变形；wc(it,iz)为大小齿轮轮齿复合接触变形；wgs(it,iz)包括齿轮弯曲、支撑轴变形。

轮齿变形可由式(12)计算求得：

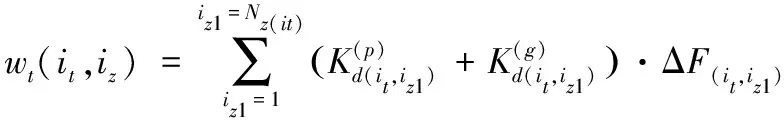
(12)

(13)

(14)

2.2 有限元提取最大接触应力数学模型

根据参考文献[8] ，通过式(15)来确定轮齿it上iz小段的法向最大接触应力：

(15)

fσr0(hDr,hFr)·fwa0(bDr,hFr)

2.3 有限元提取传递误差数学模型

总传递误差包含齿轮副安装运动误差、轮齿误差变形误差等。假设齿轮1为主动轮并以恒定角速度运转。由于齿轮副的安装、运动误差导致齿轮副间的角速度比不断变化，且从动轮的角位移将偏离理论位置，则从动轮角位移可以由式(16)表示：

(16)

式中：Φ1、Φ2分别为齿轮1、2的瞬时角位置；Φ10、Φ20分别为小齿轮、大齿轮的初始角位置；N1、N2分别为小齿轮、大齿轮的齿数；ΔΦ2s为由于装配误差引起的大齿轮的角位移。

根据式(4)计算大小齿轮啮合过程中由于柔量变化引起的大齿轮角位移。因此，齿轮总传递误差由式(17)计算：

(17)

3 有限元分析

3.1 螺旋锥齿轮模型的建立

螺旋锥齿轮参数较多且建模复杂，为精确建模，本文通过CATIA软件中二次开发功能模拟螺旋锥齿轮真实的加工过程，通过切割来获得1个齿槽包络线模型，从而获得螺旋锥齿轮的齿廓曲面和齿根曲面。以切割轨迹线的端点为采样点，用二阶连续的双三次非均匀有理B样条(NURBS)拟合获得光滑的拟合曲线，从而重构出曲率均匀变化的齿槽曲面。通过阵列等操作可构建出精确的螺旋锥齿轮几何模型。

图3 螺旋锥齿轮有限元装配模型

3.2 螺旋锥齿轮静力学有限元分析

有限元分析前处理设置关系将取决分析结果的准确性，螺旋锥齿轮选常用合金钢材料，弹性模量206 000MPa，泊松比0.3，齿轮接触选择有限滑移接触算法，硬接触，摩擦系数值为0.06。端面滚刀加工螺旋锥齿轮完成后，根据齿轮实际负载，分析不同加工参数对接触应力及传递误差的影响，以获得降低齿轮接触应力及传递误差的方法，分析结果如图4所示。图中参数Kpmax(实心圆圈表示)、KΔΦ2max(实心方框表示)分别表示不同加工参数下加工所得螺旋锥齿轮最大接触应力、最大齿轮传递误差与理论共轭啮合条件下加工螺旋锥齿轮相应值之比。

观察图4(a)可知，刀具倾角一定时，随着刀具旋转角的增加，螺旋锥齿轮最大接触应力急剧增加；传递误差缓慢降低最后趋于稳定；同时可以明显看出，随着旋转角的减小，锥齿轮最大接触压力几乎不变；传递误差先降低，再增加最后趋于稳定。

由图4(b)可知，保持刀具其他参数一定，随着倾斜距离(hd)的增加齿轮最大接触应力缓慢降低、齿轮传递误差先降低后增加；然后随着倾斜距离的减小齿轮最大接触压力几乎呈直线下降，齿轮传递误差趋势表现为直线增加。

图4(c)表明随着机床修正量(Δe)的增加齿轮最大接触压力缓慢增加、传递误差则缓慢降低；随着修正量的降低，齿轮最大接触压力急剧下降，随后趋于平稳、齿轮传递误差则表现为急剧增加。

由图4(d)可知随着刀头半径的增加(Δrt0)齿轮最大接触应力将至最低后缓慢上升、传递误差则呈现出先降低后急剧增加的变化趋势。

图4(e)、图4(f)分别表示刀盘内、外圆弧刀刃半径(rprof1、rprof2)对齿轮最大接触应力、传递误差的影响。由图4(e)、图4(f)可以发现刀盘内外圆弧半径对齿轮最大接触应力、传递误差的变化趋势相同：随着内外圆弧半径的增加，最大齿轮接触应力虽然有些波动，但整体表现较为平稳；齿轮传递误差则在内外圆弧半径增加最初阶段急剧降低，然后变化开始趋于平稳。

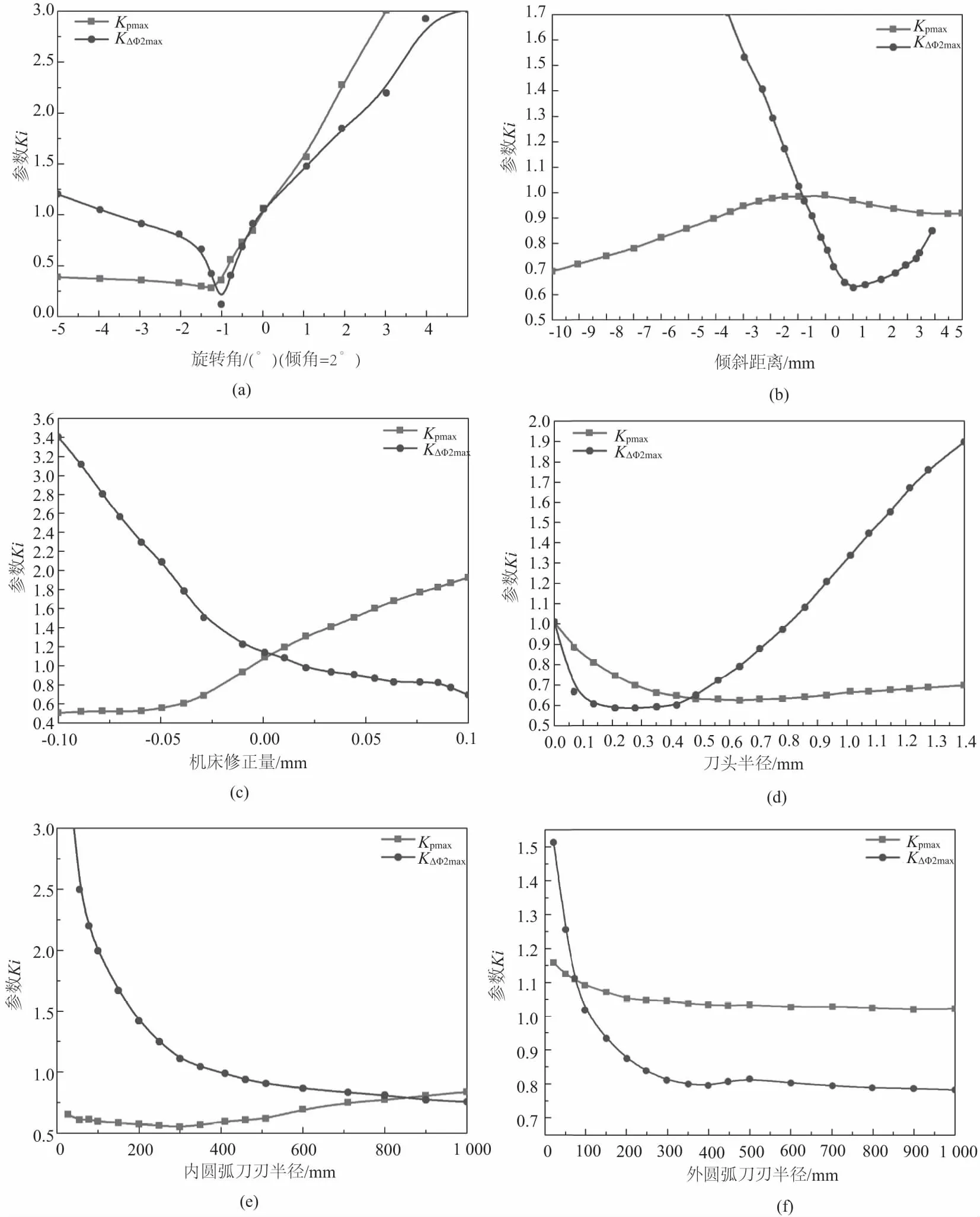
图4 不同加工参数对接触应力及传递误差的影响

根据图4分析，当κ=2°，μ=-1°时，齿轮传递误差、齿面接触压力最低。

3.3 螺旋锥齿轮动力学有限元分析

动态加载分析采用与静力学分析相同的有限元网格模型，但分析类型选择动态显式分析算法。根据静力学分析得到的参数，进行纵向分析不同工况下(如表1所示)齿轮最大接触压力及传递误差随齿轮传动比变化的趋势，分析结果如图5所示。

表1 不同加工工况

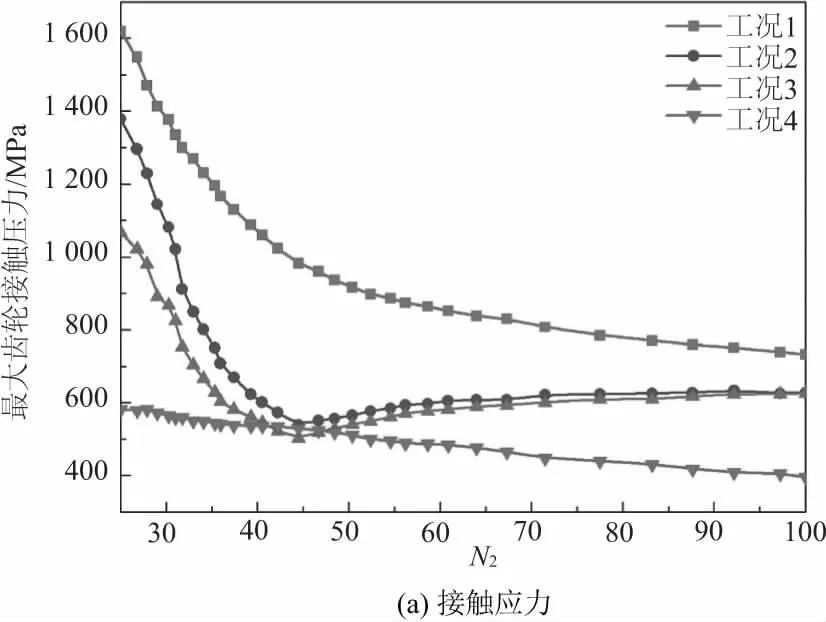
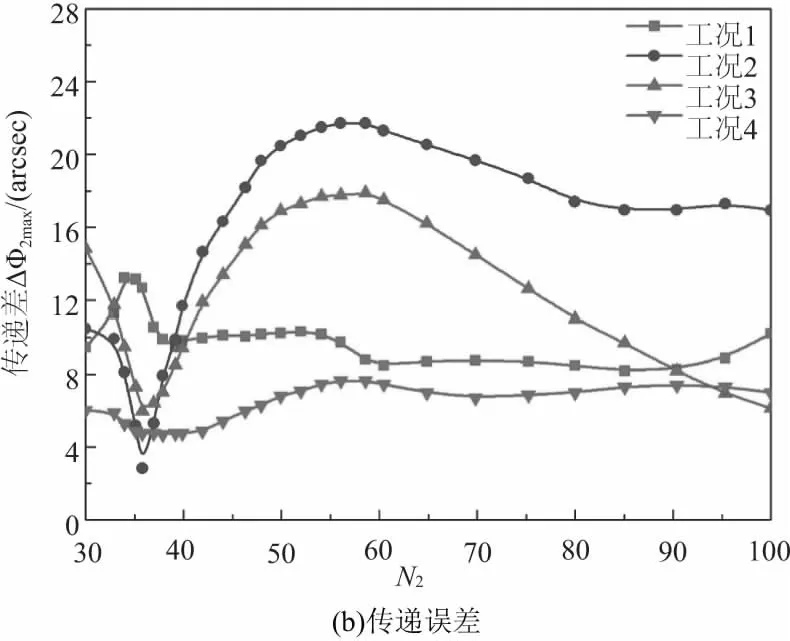
图5 不同工况下分析结果

图5为不同加工工况下，最大齿轮接触压力、传递误差分析结果。分析图5可知加工工况完全相同时，最大齿轮接触误差随着齿轮传动比的增加而降低；传递误差随传动比的变化比较复杂。

分析图5(a)可知，刀具旋转角、倾角一定时，改变加工工况均降低了最大齿轮接触应力；其中工况4加工条件下最大齿轮接触应力降低最为明显，且随传动比的增加，最大齿轮接触应力呈线性降低的变化趋势。

观察图5(b)可以发现，传动比较小时，改变加工方法有利于降低齿轮传递误差；然而随着传动比的增加，完全共轭加工条件下齿轮传递误差几乎没有变化，工况2、3条件加工下齿轮最大传递误差均呈现先急剧增加后逐渐降低的变化趋势，且两种工况下加工的螺旋锥齿轮传递误差在传动比较大时均比工况1高。工况4则表现出较好的传动平稳性，传动比较小时明显低于工况1，随着传动比的增加该工况下齿轮传递误差缓慢增加最终趋于稳定。

根据以上分析结果，以工况4为研究对象，分析不同N1对最大齿轮接触压力、齿轮传递误差的影响，分析结果分别如图6、图7所示。图7为N1=10时最大齿轮接触压力及齿轮传递误差分析结果。对比图5、图6工况1可以看出，随着主动轮齿数的减小最大齿轮接触压力变化不明显；然而传递误差却较工况1明显变大。

图7为N1=16时分析结果。对比图6、图7可以发现，随着主动轮齿数的增加，最大齿轮接触压力急剧降低，对比传递误差发现传递误差也得到了很大程度的改善。

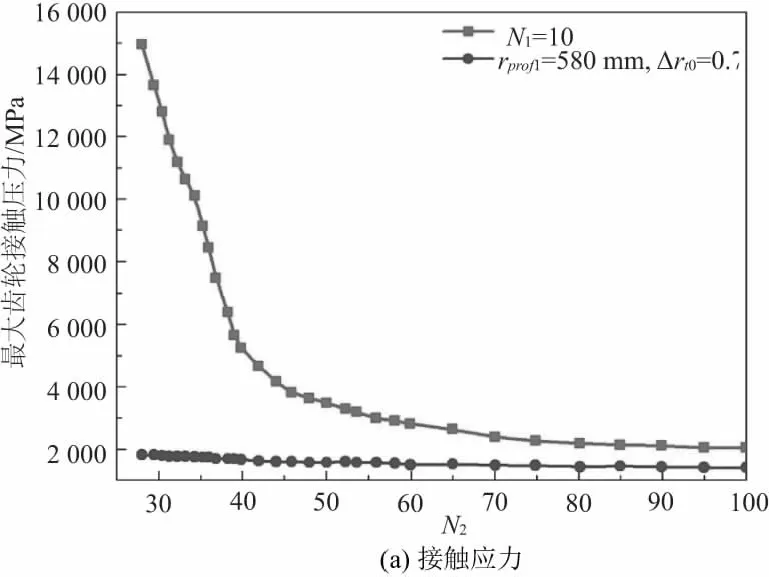
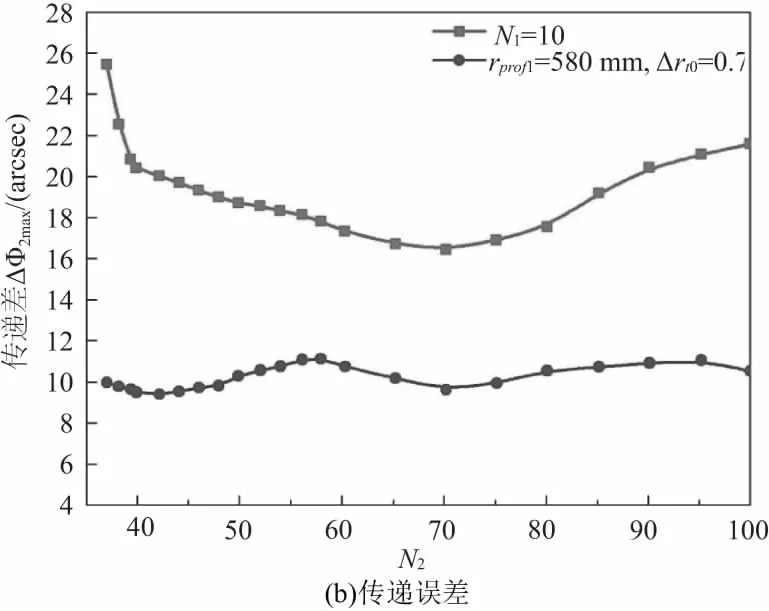
图6 主动轮齿数N1=10分析结果

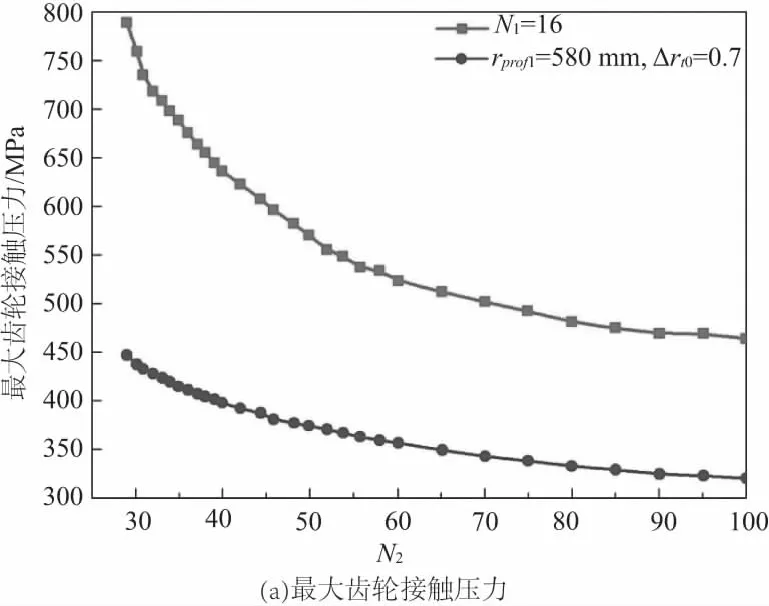
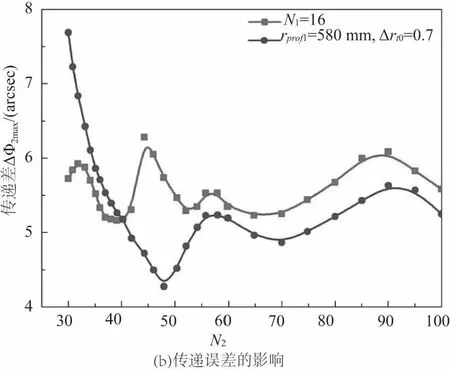
图7 主动轮齿数N1=16分析结果

3.4 实际加工验证

通过对螺旋锥齿轮副的实际工况加载，获得实际转速和转矩工况变化规律，反映出大致的螺旋锥齿轮啮合特性，并利用计算机的数据处理功能，获得螺旋锥齿轮副传动误差的变化规律。另外，再通过对滚机对齿轮的接触区域进行着色检测，检查实际接触区域的大小和位置，从而真实地反映实际啮合传动过程中的接触性能。

图8 实际传动误差和实际接触区域

如图8所示，螺旋锥齿轮的传动误差比较小，波动范围约为0.1rad，接触区主要集中在齿宽中间区域，接触性能良好，与有限元的分析结果一致，螺旋锥齿轮副传动平稳，说明有限元理论分析的可靠性。

4 结语

1) 通过引入假想共轭啮合齿轮，构建加工过程中螺旋锥齿轮齿面方程，然后基于坐标变换提出螺旋锥齿轮最大接触应力及传递误差的有限元数学模型；

2) 刀具倾角为2°、旋转角为-1°时，齿轮传递误差、齿面接触压力最低；内圆弧刀刃半径为580mm的加工方式将大大改善该螺旋锥齿轮最大接触应力及传递误差；

3) 主动轮齿数的增加会很大程度上降低螺旋锥齿轮最大接触应力及传递误差。