流域初始水权分配的博弈研究
耿鸿江
(云南水利水电职业学院,昆明 650400)
1 流域初始水权分配的博弈特征
我国的水资源作为公共资源具有公开获取性和非排他性,即流域内所有用水户均有共享流域内水资源的权利,而不能互相排拆,因此在流域水资源评价的基础上合理分配初始水权,是建立水市场、实现水资源优化配置的一项基础性工作[1]。
在初始水权分配时,用水户各方均从自身利益出发要求多分配水权,在流域水资源承载能力一定的前提下,追求用水效益最大化的各用水户间不可避免地产生用水冲突和纠纷,使流域初始水权分配具有比较典型的博弈特征[2]。
1.1 流域初始水权博弈的基本要素
1) 参与者。流域内用水利益主体,简称用水户,包括用水个人、法人、单位或行政区域。
i∈I,I=(1,2,……,n)。
2) 策略。博弈参与者(各用水户)对初始水权分配的选择方案或措施,如彼此合作,相互考虑协同的水权分配额q;彼此不合作,各行其是,只考虑自身利益的非协同水权分配额q+Δq,Δq为要求增加的部分初始权,其策略空间为Si={协同,非协同}。
3) 收益函数。用水户的用水效益随用水量的增加而增加,但增加速度将减慢,其收益函数μ(q,m)=1-e-mq,其中m为大于0的参数。
1.2 用水收益函数分析
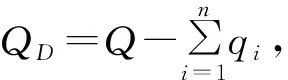
(1)
ml随着Δq减少而增加,当Δq=0时,ml=mh。
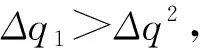
如果k 图1 流域用水收益函数曲线 为了研究方便,将流域内用水户概化为两个,其自然状态下初始水权分配博弈见表1。 表1 自然状态下流域初始水权分配博弈 由式(1)得: (q-Δq)mh<(q+Δq)ml (2) 则u(q+Δq,mh)>u(q,mh)> u(q+Δq,ml)>u(q-Δq,mh) (3) 由表1可知,无论用水户1选择什么策略,用水户2的优势策略均为非协同;同样无论用水户2选择什么策略,用水户1的优势策略也都为非协同。因此,两个用水户初始水权分配博弈的纳什均衡为{非协同,非协同},彼此的收益之和 2u(q+Δq,ml)小于彼此均选择协同策略的收益之和2u(q,mh)。这说明,每个用水户都从自身利益出发,都要求增加初始水权Δq,结果流域的公共水权减少2Δq,水资源过度开发,全流域的收益参数由mh下降为ml,整个流域的水资源利用是低效率的,最终导致流域初始水权分配走进了“公地悲剧”型的“囚徒困境”。 根据纳什均衡原理,作为公共资源的水资源,在自然状态下的开发和利用,其结果一定是一种满足个人理性纳什均衡。也就是说如果没有有效的机制安排,用水户均选择“非协同”策略的“囚徒困境”必然存在。 流域初始水权分配不会一次完成和固定不变的,在用水户不断的变化和纷争中,初始水权分配会经过无数次调整,形成一个无限期或期限不确知的动态重复博弈过程,这时用水户就会考虑自己当前行动对将来的影响,而自己将来的收益又和其他用水户的利益相关联。设δ为某一用水户的贴现因子,在初始水权分配的重复博弈中,用水户选择“冷酷战略”,对不合作的非协同用水户进行惩罚。即在重复博弈开始时,双方均选择协同策略,而如果某一方在某阶段背叛,选择了非协同策略,则另一方一气之下,永远不与之合作,一直选择非协同策略[3]。如果用水户一直选择协同策略,那么它的期望收益为: UC=u(q,mh)+δu(q,mh)+δ2u(q,mh)+… (4) 如果某一用水户选择了非协同策略,导致另一方采取“冷酷战略”进行惩罚,那么这个用水户的期望收益为: UD=u(q+Δq,mh)+δu(q+Δq,ml)+ δ2u(q+Δq,ml)+… (5) 由Uc>UD得: (6) (7) 可见,当δ足够大,即用水户在重复博弈中有足够的耐心时,Uc>UD,整个流域初始水权分配的集体理性合作解{协同,协同}战略就会出现,且有: u(q,mh)>δu(q+Δq,ml)+(1-δ)u(q+Δq,mh) (8) 显然当δ=0,式(8)不成立,这个不等式要靠无限期重复博弈(或次数不确定)及δ足够大(足够耐心)的惩罚项u(q+△q,ml)来维持,这就是流域初始水权分配的内在反应机制。 上述用水户的内在反应机制虽然能使流域初始水权分配出现集体理性的合作解,但要求博弈无限期重复或不确知何时结束,同时博弈各方要有足够的耐心。这两个条件较为苛刻,在当前的社会条件下很难满足,因此有必要引进外在力量,对博弈进行介入和干预,以打破纳什均衡的“囚徒困境”,实现个人理性和集休理性的统一[4]。 在初始水权分配中,作为水资源所有权和公共水权代表的水行政执法部门,通过必要的经济手段进行干预和调节[5],以体现初始水权分配中的效率、公平与和谐,最终实现流域社会经济与资源环境的可持续发展[6]。 假设对同时选择非协同策略的用水户各惩罚F(F>0);一方选择协同,一方选择非协同的,则补偿协同方因非协同方不合作行为而造成的损失(1-e-mhq)-(1-e-mh(q-Δq)),同时惩罚非协同方x,在水行政执法部门的经济调节下,初始水权分配博弈见表2。 表2 水行政执法部门经济调节下的流域初始水权分配博弈 采取不合作的非协同策略所获得的“不义收益”为: x*=u(q+△q,mh)-u(q,mh) =e-mhq(1-e-mhΔq)=e-mhqu(Δq,mh) 因此,只要x>x*,即对非协同方惩罚力度大于其“不义收益”时,才会抑制非协同方的贪欲,促进彼此协同合作,达到集体理性的合作解,从而使初始水权分配和全流域水资源配置实现最优状态。 如果因某种原因,外力介入的经济调节制度没有建立起来,或者没有有效实施,用水户又没有足够的耐心进行无限期重复博弃,在水资源承载能力一定的前提下,用水户间初始水权分配之争不可避免地发生,水行政执法部门不得不介入,进行行政干预或仲裁[7]。 (9) 双方推断Δq2被裁中的概率为: (10) 则Δq1被裁中的概率为: (11) 因此,初始水权期望水平为: (12) (13) 根据纳什均衡,给定Δq2,用水户1追求增加的水权最大化,即: (14) 一阶条件为: (15) 给定Δq1,用水户2追求减少初始水权最小化,即: (16) 一阶条件为: (17) 联解式(15)、式(16)得: (18) (19) (20) 由此得到用水户双方初始水权分配争议的纳什均衡解为: (21) 2012年5月,云南威信县人民政府争取到中国烟草总公司云南省公司2 400万元投资,兴建烟水配套工程,用于解决威信县麟凤、长安镇近5 000人的饮水和360 hm2烟田灌溉用水困难。其中部分取水点属于镇舟河流域,该工程取水影响到镇舟河下游四川省筠连县群众用水,工程开工后不久,遭到四川筠连县群众破坏,由此引发两省水权纠纷[8]。 纠纷发生后,威信、筠连两地政府及水利部门多次协商未果,由于冲突双方都急于追求各自利益的最大化,因此解决水权纠纷的用水户内部反应机制,在现实条件下难以奏效,冲突双方一度陷入“囚徒困境”。 由于双方协调未能达成一致,筠连县向长江委员会举报此事,长江委责成两省水行政主管部门分别调研、取证、协调沟通,并配合长江委工作组现场勘查。2013年8月,长江委组织两省召开协调会,提出了兼顾上下游左右岸利益为核心的“五项调处原则”,保证上游威信县年取水64×104m3的正当用水权益,在枯水期保证饮用水的前提下,充分考虑下游的用水需求,如果仍然无法达成共识,则建议流域机构作出上下游水量分配方案。 此次调解在保证两地生活用水的基础上,兼顾上下游的用水效益,争取两地利益均衡,是双方利益的折中方案,使冲突双方的损失达到最小,并使两地受益均衡,变幅可控,体现了纳什均衡原理。由于有长江委的介入和干预,打破了纳什均衡的“囚徒困境”,实现了个人理性和集休理性的统一,最终双方本着互惠互利、人水和谐的原则,都表示愿意接受这一调处,一度激化的冲突双方得到了圆满的解决。 这个实例说明,水资源统一管理和初始水权分配的重要性,尤其是界河,事先一定要编制水资源综合利用规划,界定初始水权,并建立以博弈论纳什均衡为思想基础的外在干预机制,以实现水资源开发利用和谐、有序和可持续发展。 通过对流域初始水权分配的博弃分析,得到如下基本结论: 1) 水资源是公共资源,具有公开获取性和非排他性。根据纳什均衡原理,在自然状态下,初始水权分配的争议和水资源无序过度开发利用的“囚徒困境”现象不可避免。 2) 用水户间的重复博弃可以解决初始水权分配的“囚徒困境”,但要求同时具备博弃的无限期(或不确知何时结束)和用水户有足够的耐心,即贴现因子足够大。在当今的社会条件下,用水户不可能满足这两个条件,因此用水户间的内在反应机制很难实现。 3) 通过外在力量介入可以打破初始水权分配的“囚徒困境”,其行政手段虽然可以使争议双方达到满意的纳什均衡调解,但从实现整个流域水资源优化配置的角度来看,其经济手段更为有效,但要求其惩罚力度一定要大于非协同方的“不义效益”。 4) 机制和制度安排是水资源优化配置的关键,必须建立相互理解信任与合作的长效机制,使博弃多方能自我约束和自我实现,最终达到集体理性的整个流域水资源可持续利用。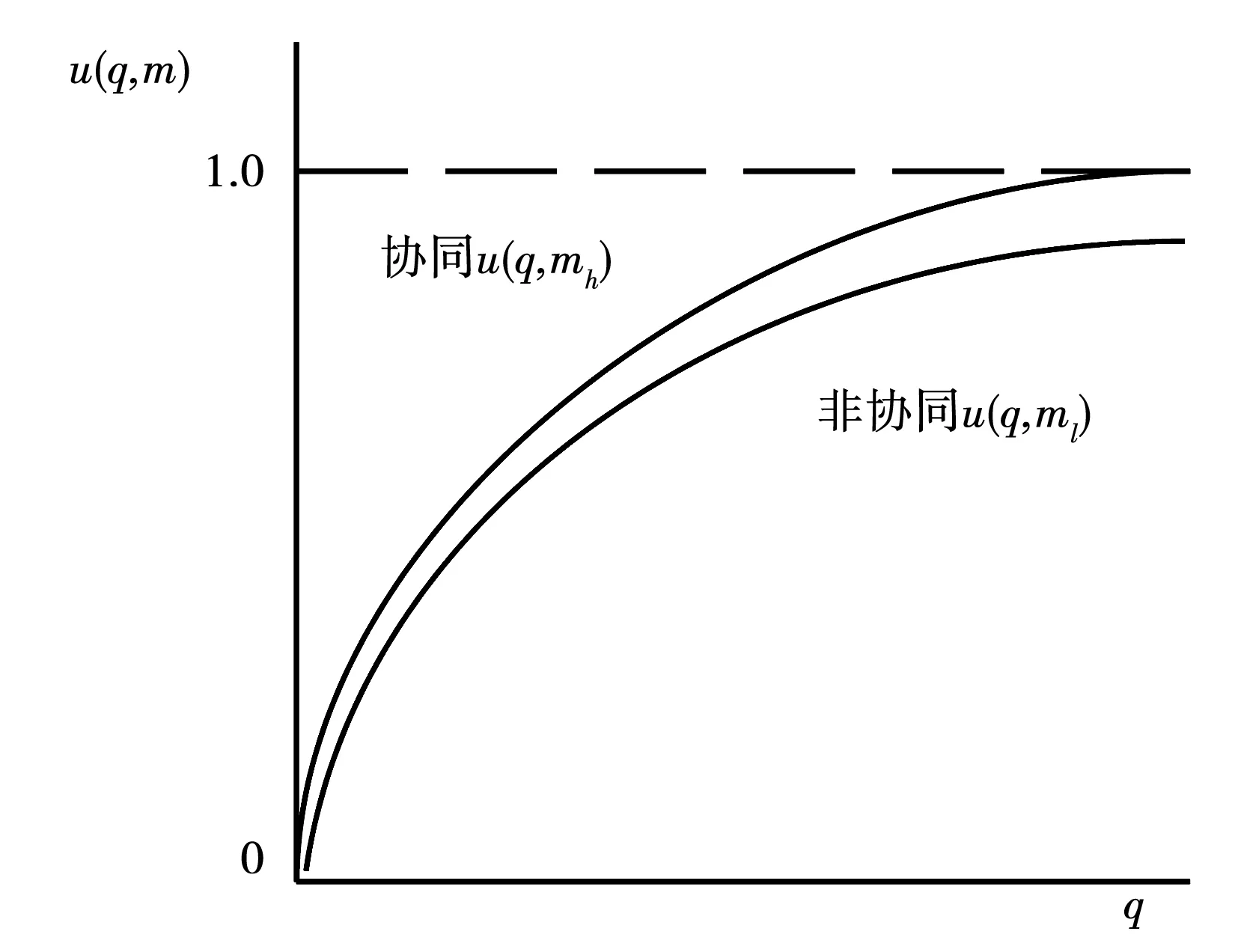
2 流域初始水权分配的“囚徒困境”

3 流域初始水权分配的内在反应机制
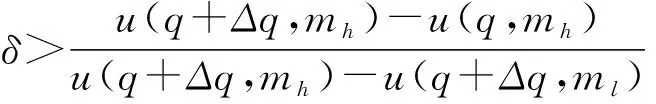
4 流域初始水权分配的外在干预机制
4.1 水行政执法部门的经济调节制度

4.2 水行政执法部门的行政调节制度
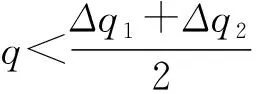
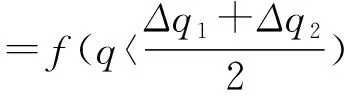
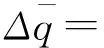
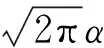
5 实 例
6 结 论

