基于季节指数的城市轨道交通月度客流预测方法*

王夏秋 张 宁 王 健

(1. 东南大学智能运输系统研究中心轨道交通研究所， 210096， 南京；2. 南京地下铁道有限责任公司， 210024， 南京//第一作者，硕士研究生)

短期客流预测指预测1年内(主要以小时、日、月、季度等时间单位作为时间粒度)的轨道交通网络或者线路的客流特征、服务水平以及出行效率等[1-3]，是城市轨道交通运营部门展开各项管理工作的基础与依据。在以往的短期客流预测研究中，主要集中于短期客流的日/小时预测[4-5]，而对于月度或季度等更长时间跨度的短期客流预测还少有研究。但在城市轨道交通的实际运营中，车辆月度检修计划、运用车配备计划以及日常运输计划的调整等大型生产计划需要参考月度、季度客流预测的结果，同时，运营企业可根据该预测结果合理制定年度/季度生产运营计划。有鉴于此，本文针对月度客流预测展开研究。

与小时/日客流不同的是，城市轨道交通月度客流受偶然因素影响的随机波动性不大，但因预测的时间跨度较大，其受季节气候变化、法定节假日分布、学校寒暑假等较稳定因素影响呈现出季节性波动的周期性特征[5]。因此，针对月度客流量呈现的明显季节性特点，引入季节指数对原始月度客流数据进行季节处理，以季节调整原始数据并利用自回归积分滑动平均(ARIMA)模型对城市轨道交通月度客流进行预测，从而使构建的预测模型具有更好的预测精度，提高预测结果的准确度。

1 月度客流特性分析

现代城市轨道交通系统采用自动售检票(AFC)系统记录乘客的交易数据，是获取轨道交通客流数据的良好平台，为月度客流特性分析和城市轨道交通短期客流预测工作提供了数据支撑。本文采用的城市轨道交通运营客流数据来自于南京地铁自动售检票系统，以月份为统计时间间隔，南京地铁2号线月度进站客流的时间演变如图1所示。

a) 年度时间序列

b) 月度时间序列图1 网络化运营后的南京地铁2号线月进站客流演变图

由图1可见，月度客流量有以下变化特征：

(1) 趋势增长性。图1 a)年度时间序列反映的是月度客流量在同一月份不同年份的变化情况，体现了客流量随着沿线土地开发利用逐渐实施与完善以及网络化运营效应的影响所呈现出的增长趋势。具体表现为在相邻的两个年份之间，其客流量具有相同的分布特性，且随着城市经济的发展，客流总体随着各月份呈现出增长趋势。

(2) 季节波动性。图1 b)月度时间序列反映的是月度客流量随着时间的逐渐推移呈现出不同的变化情况，体现了该月度客流量由于季节变化的不同而引起波动的发展趋势。具体表现为：由于春节假期原因，客流量在每年1、2月份出现低谷；7、8月份受到炎热天气以及学生放假的影响，其客流量略少于其他月份。因此，月度客流量每年重复出现循环变动，即以12个月为周期的季节波动性。

从图1可以发现，城市轨道交通月度客流受偶然因素影响的随机波动性不大，但因预测的时间跨度较大，一方面，受季节气候变化、法定节假日分布、学校寒暑假等较稳定因素影响，呈现出季节性波动的周期性特征；另一方面，在无新线接入的条件下，主要受线路周边土地开发利用程度和网络化运营效应影响而呈现趋向于线性但不够平稳的趋势增长性特征。考虑到季节指数法能够有效地消除季节性因素影响，且ARIMA模型是线性估计模型，其对线性且非平稳性时间序列数据能进行较好的处理，因此，结合两种模型的优势，引入季节指数法和ARIMA模型共同对城市轨道交通月度客流量进行预测，从而使构建的预测模型具有更好的预测精度，提高预测结果的准确度。

2 基于季节指数的ARIMA模型

2.1 季节指数

形成以12个月为循环周期的这种季节性波动最主要的因素是自然季节性和制度季节性的综合影响。其中，自然季节性是一年中气候、光照时长、温度等因素变化的结果；而制度季节性则是由于法定节假日及一些特殊时期的活动引起的，尤其是法定节假日是制度季节性的最一般性的表现。正是由于这两种因素的叠加，形成了我国城市轨道交通月度客流季节性波动的独特性。因此，需要从该时间序列中剔除季节因素，在建模预测前引入季节指数调整[6]，建模预测过程中对预测值用季节指数逆向季节调整，使预测结果更符合客观规律[7]。

季节指数是基于统计学的一种简化时间序列数据的方法，通过该方法对季节时间序列的季节性进行处理，同时使得原始数据中的一些重要信息不被丢失。本文采用的是直接平均季节指数法对原始客流数据进行建模前的季节指数调整。直接平均季节指数法用算数平均值直接计算各月或各季度的季节指数[6]，其计算公式为：

(1)

式中：

cj——第j个月的季节指数；

xij——第i年第j个月份的客流量。

然后利用该指数对历史各月份的月度流量xij进行季节调整：

(2)

经过对历史数据的处理之后，通过预测得到未来时期某个月份的客流总量为yj，那么逆向季节调整后的该月客流总量为：

(3)

2.2 ARIMA模型

ARIMA模型是将非平稳时间序列通过差分计算转化为平稳序列后，将因变量仅对其滞后值及随机误差项的现值和滞后值进行回归建模[8]。由此可知，ARIMA模型是对时间序列进行差分转化、自回归、移动平均的一种预测方法，故ARIMA(p,d,q) 称为差分自回归移动平均模型。其表达式为：

xt=φ0xt-d+φ1xt-d-1+…+φpxt-d-p+εt-

θ1εt-1-θ2εt-2-…-θqεt-q

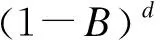
(4)

式中：

xt,xt-1,…,xt-p——观测序列值；

B——延迟算子；

{εt}——零均值白噪声；

φ0，φ1,φ2,…,φp，θ1,θ2,…,θq，εt——均为待估参数；

p——自回归项；

q——移动平均项数；

d——时间序列成为平稳时所做的差分次数。

2.3 基于季节指数的预测步骤

基于季节指数的ARIMA模型的短期客流预测是先通过季节指数调整原始客流序列后，再通过差分处理将序列平稳化，最终将其转化为ARIMA模型来解决。主要预测步骤如下：① 计算季节指数并调整月度客流序列。根据数据优化处理方法，利用原始客流数据计算各月份的季节指数，并用计算得到的季节指数按照式(2)对样本中的各月份客流量进行季节调整，以获得变换后的月度客流序列。② 利用经过变换后的客流序列建立ARIMA模型。将经过变换后的客流数据按照数据平稳化处理、模型识别、参数估计和检验这三步构建出合适的ARIMA模型。③ 利用季节指数逆向季节调整预测值。利用上一步得到的模型预测未来时期某个月份的客流量，并按照式(3)对预测值进行逆向季节调整，得到的结果即为最终的月度客流预测值。

3 实例分析

3.1 数据来源及处理

本文选取网络化运营稳定后南京地铁2号线2011—2013年共36个月的进站客流量为基础数据，通过本文计算方法对36个月的原始月度客流时间序列数据进行计算，得到季节指数(如表1)。

表1 月度客流时间序列的季节指数

根据表 1的季节指数，对原始客流序列进行季节调整，经过变换后的月度客流序列如图 2所示。

3.2 结果及讨论

利用变换后的月度客流序列构建ARIMA(1,1,1)(0,1,0)12模型，对月度客流量进行预测，得到的预测结果如表 2所示。同时，为验证本文提出的预测方法的有效性，将原始数据直接建模预测得到的结果与之对比分析，有无季节指数调整的ARIMA模型预测结果如表 2所示。

表2 有无季节指数调整的预测结果

通过相对误差(PE)和平均绝对百分比误差(MAPE)两个指标来检验两个模型的预测精度，其性能评价指标结果如表3所示。

表3 有无季节指数调整的ARIMA模型误差对比分析 %

进一步地，得到有无季节指数调整的预测客流趋势曲线与实际客流曲线对比，如图3所示。

图3 2014年1—6月有无季节指数调整的预测客流趋势曲线与实际客流曲线对比图

通过两个指标对比分析可见，基于季节指数的ARIMA模型预测各月度客流量的相对误差较无季节指数调整的ARIMA模型的相对误差好，均在10%以内，有些月份的相对误差更达到了2%以内，相对误差主要在5%范围上下波动，平均绝对误差也在5%以内。 对于个别月份的相对误差比无季节指数调整的ARIMA模型预测结果的误差值大(如2月份和5月份)，是因为2014年的春节处于2月份，期间客流出行受走访探亲、购物、旅游等多种随机因素的综合影响，且历史年的春节并非都处于2月份，仅通过季节调整而不考虑日历因素影响得到的预测结果，反而比单纯利用ARIMA模型预测的结果误差更大，未来可考虑加入日历因素影响因子以提高预测结果的准确度。而2014年5月31日南京为迎接青奥会的到来在南京玄武湖举办环湖大型徒步活动，致使当日客流量较历史同期的客流量大幅度增加，进而影响5月份的客流总量。与此同时，图3的趋势曲线表明，相对于无季节指数调整的预测客流趋势曲线而言，基于季节指数调整的预测客流趋势曲线与实际客流曲线更加吻合。综上所述，基于季节指数的ARIMA模型预测效果更佳。

4 结语

本文提出的基于季节指数的预测方法是在采用ARIMA 模型建模预测前引入季节指数对原始客流数据进行季节调整，以消除季节因素对建模的影响，并在预测结束后用季节指数对预测值进行逆向季节调整，使预测结果更加符合客观规律。通过与未经过季节指数调整的ARIMA模型预测结果对比分析，说明了本文提出的方法在月度客流预测中精度较高，基本满足对客流量的预测需求。运营单位可根据该方法得到的预测量及时调整相关运能运力，制定更加经济合理的季度或年度运营计划。需要指出的是，基于季节指数的ARIMA模型适用于具有周期性变化规律的客流量预测，而以小时、天等更小的预测时间跨度也具有一定的周期波动性，未来可尝试采用该模型进行预测。