基于Spark的大数据三枝决策分类方法

刘牧雷, 徐菲菲

(上海电力学院 计算机科学与技术学院, 上海 200090)

决策速度和决策正确性是决策问题的两大核心要素。对于单一的决策问题,当决策方式为确定时,每一次决策可认为是独立决策。所以,对与海量的不相关数据,可以使用并行化的方式来进行决策。对于决策准确性问题,YAO Y Y教授以粗糙集理论为基础,提出了三枝决策理论[1-2]。相较于传统决策理论,三枝决策理论更加贴合人们在实际生活中的决策方式,并且在代价敏感决策问题上有着更好的表现[3-5]。

在一般的数据集中,数据对特征的相关程度并不是均匀的。因此,对于数据集中特征明显的数据,只需要少量的训练就会呈现出明显的决策倾向。由此,如果对数据集的决策是分步进行的,那么在决策过程中也会提高决策的效率。

当前,无论是海量数据处理,还是并行化运算,Spark都是流行的解决方案。Spark是基于Hadoop平台的开源云计算平台,目前广泛应用于生产实践中。Spark通过MapReduce[6]计算模型实现并行计算,通过弹性分布式数据集(Resilient Distributed Dataset,RDD)数据模型实现适合于分布式平台的数据结构。

本文将三枝决策理论与Spark的MapReduce模型相结合,对数据进行并行处理,以提高三枝决策理论的效率,提升决策的准确率。

1 相关理论概述

1.1 三枝决策

三枝决策是YAO Y Y由概率粗糙集理论提出的一种新决策思想。相较于传统的“是,否”二枝决策而言,三枝决策提出了一种不同但更为合理的决策思想,即当对象当前提供的信息不足以支撑决策时,采用延迟决策,等待更多信息来完成最终决策。因此,三枝决策可以规避分类信息不足时盲目决策造成的风险[7]。

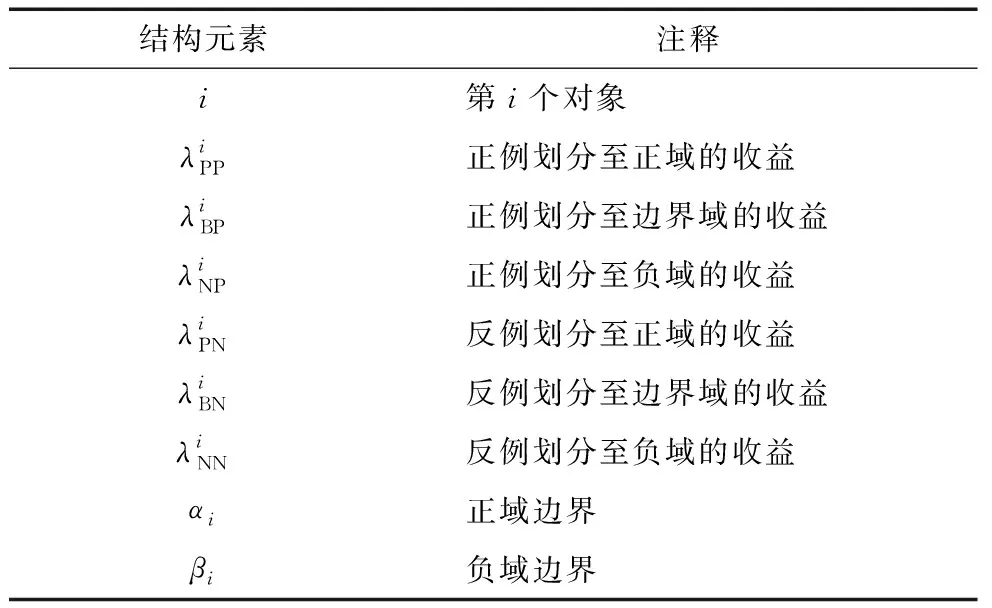
在决策粗糙集公式化描述中,X和U是全集的子集,状态集合可以表示为Ω={X,X},X和X分别表示属于X和不属于X。为了方便描述,子集和子集的状态都使用X来表示。状态X对应的动作集合为∧={P,B,N},式中,P,B,N分别表示3种判定动作,即x∈POS(X),x∈BND(X),x∈NEG(X)。三枝决策的损失函数由各个动作带来的损失决定,如表1所示。表1中,λPP,λBP,λNP表示当x属于X时采取动作P,B,N产生的损失;λPN,λBN,λNN表示当对象属于X时采取动作P,B,N时产生的损失。

表1 三枝决策的损失函数

根据最小风险决策规则可得

(P) 当Pr(X|[x])≥α时,x∈POS(X),Pr为条件概率;

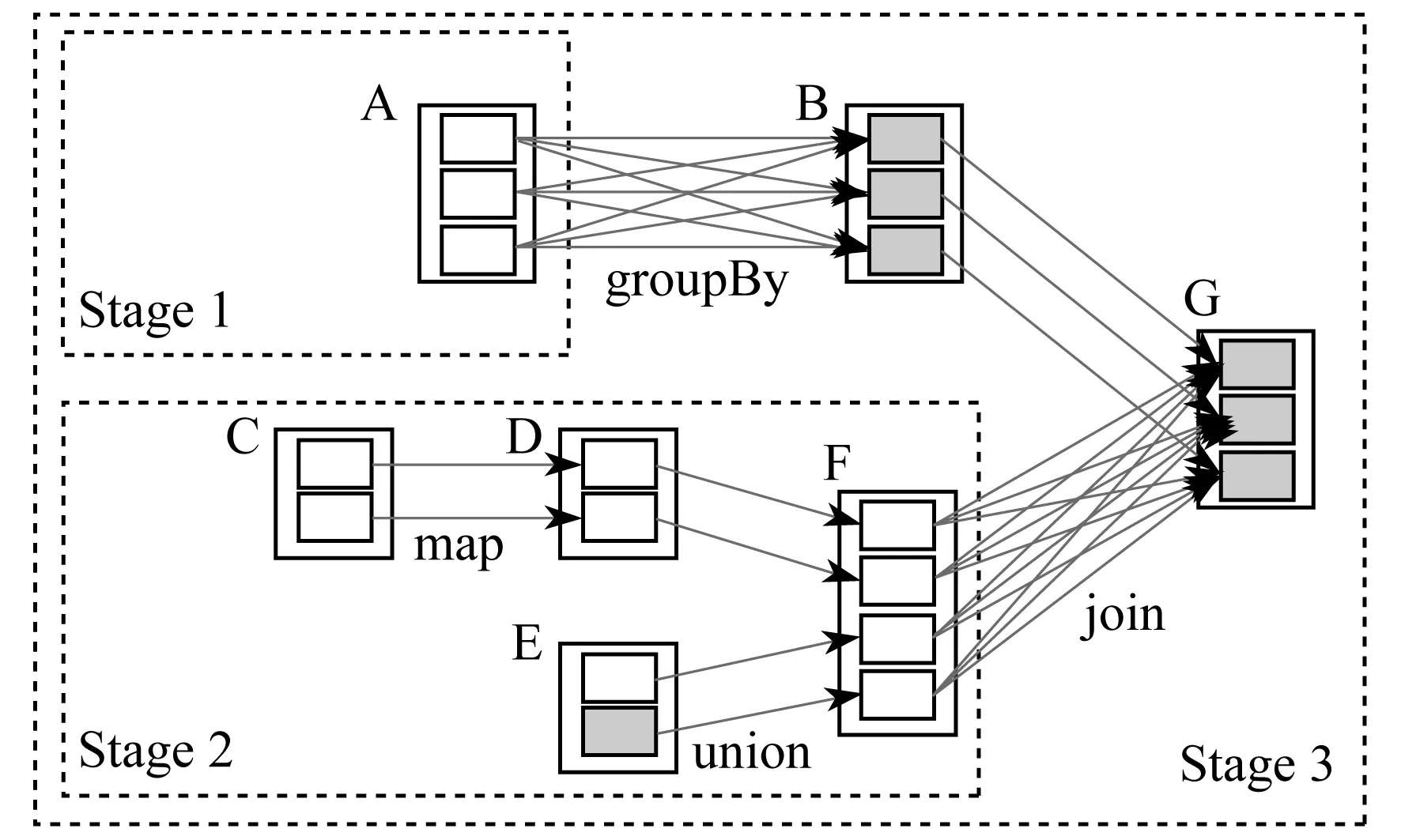
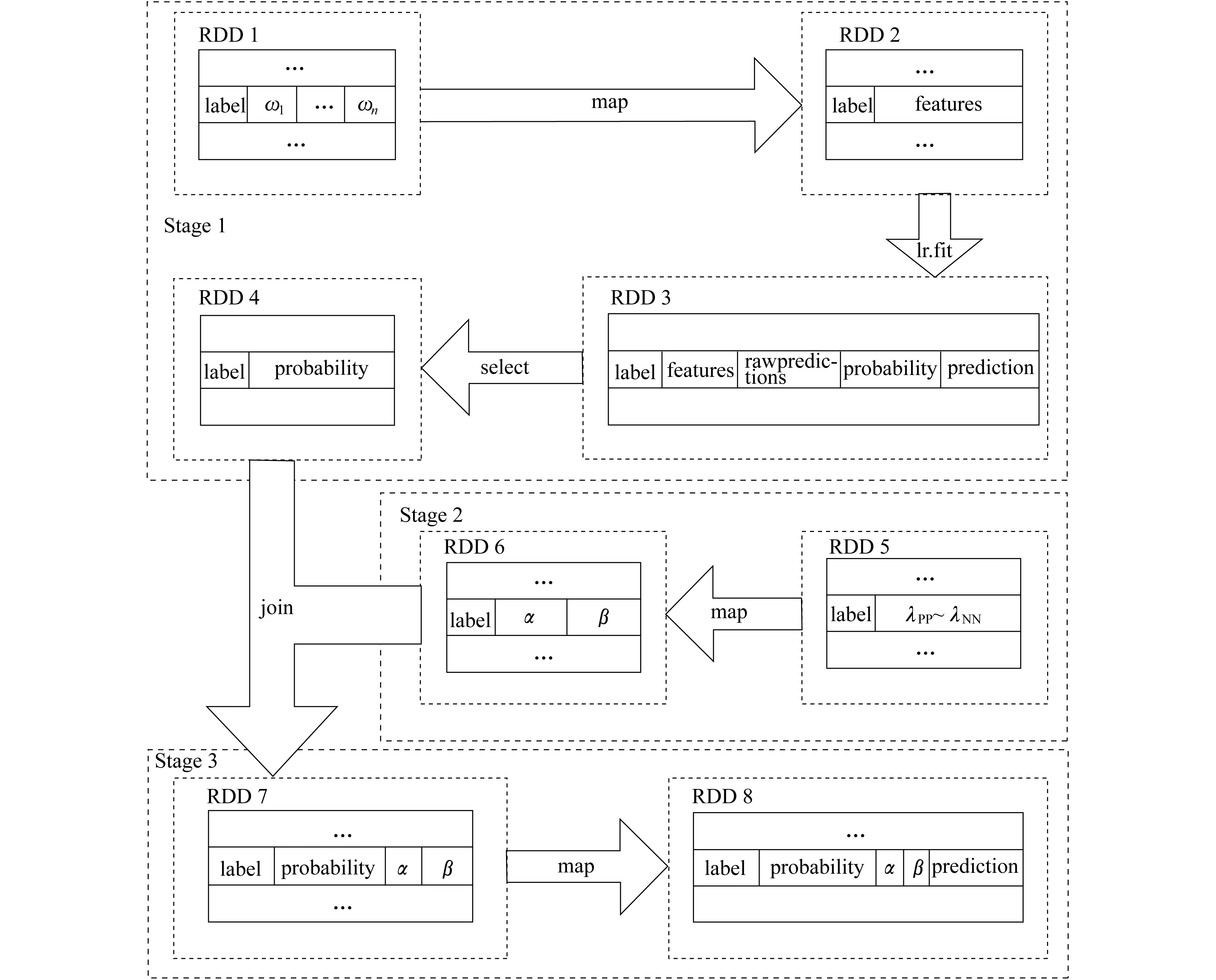
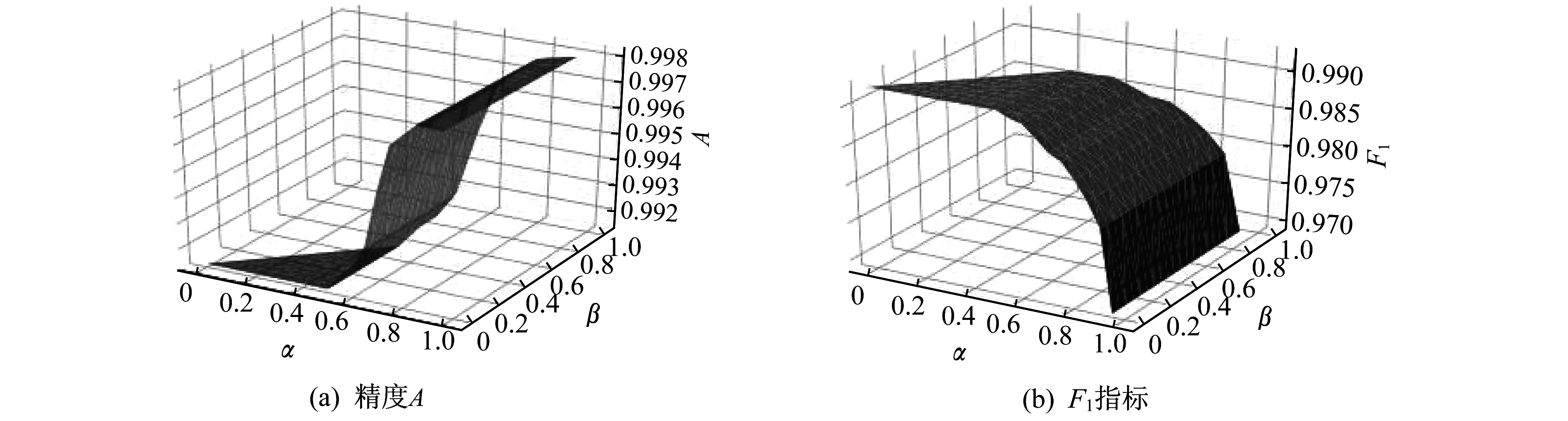
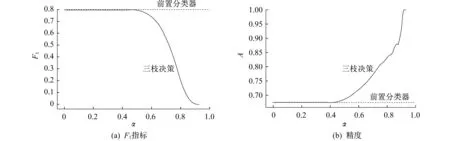
(B) 当β

(N) 当Pr(X|[x])≤β时,x∈NEG(X)。

其中

(1)

(2)

且

0≤β<α≤1

(3)

1.2 Spark与并行化

Spark是由UC Berkeley AMP Lab(加州大学伯克利分校的AMP实验室)开发的一个基于MapReduce计算模型的通用并行计算平台[8]。为了实现适合集群化的并行运算,Spark采用了RDD数据模型。RDD是Spark的核心概念,通过实现RDD模型,Spark可以进行基于内存的快速运算。图1为Spark运行时的结构示意。

图1 Spark运行时的结构示意

在Spark运行时,Driver会读取分布式存储系统中的数据块,并以RDD的形式固化在多个节点内存中。当任务启动时,Driver将会以Tasks的形式向节点分发任务,节点在完成任务后向Driver汇报Results。

RDD包括以下5个信息:一是分区信息,记录RDD的数据分区的组成;二是依赖信息,记录当前RDD是由哪些RDD变换得到的;三是计算信息,记录当前RDD是由哪些运算得到的;四是元信息,记录了整个数据分区方案;五是元信息,记录RDD存放的位置是否在内存中。

当任务启动时,Spark会根据任务,建立由多个步骤组成的DAG作为执行计划。每一个步骤包含了流水线式转换操作。整个执行计划会启动多个任务分配给每个节点,由每个节点根据自己分配到的执行计划计算各自的任务,完成任务得到目标RDD后,汇报并汇总结果。Spark的运算流程如图2所示。图2中,实线框为RDD;实心框表示RDD的分片;深色方块的表示已经在内存中的数据。当RDD G执行计算时,Spark将会建立如图2所示的DAG,并按stage1,stage 2,stage 3的顺序依次执行。

图2 Spark的运算流程

Spark的任务规划器会根据每台机器上已有的数据分片去规划任务计划,如果数据片在节点的内存里,那么直接发布任务给对应的节点;如果不在,则寻找RDD的来源。最后,所有的计算结果会发送给Driver,得到计算结果。

2 基于Spark的三枝决策算法

应用三枝决策算法的核心在于两个问题:一是条件概率Pr(X[x]R)的计算;二是阈值α和β的选取。在基于朴素贝叶斯模型的决策粗糙集理论中,条件概率是在属性间独立的假设下,利用贝叶斯理论推导出来的[9-11]。由此,三枝决策需要结合贝叶斯分类器作出判别分析后,再进行三枝决策。本文采用二元Logistic回归模型作为前置分类器,再结合Spark的分布式计算能力来实现并行化的三枝决策算法。首先,使用二元Logistic回归,计算每个样本的条件概率;然后,根据决策表中的样本选取相应的损失函数,并计算相应的阈值;最后,根据阈值与决策规则确定每个样本的最终状态。

2.1 算法介绍

首先,对于原始数据表,构建二元Logistic回归模型。在Spark中,Logistic回归模型使用Spark mllib库中的LogisticRegression类构建回归模型。建立模型的常用参数如表2所示。

表2 Logistic回归常用参数

在通常情况下,用scala语言描述建立的LogisticRegression模型的步骤如下:

(1) //建立一个迭代100次,不进行标准化、正则化、不使用弹性网络的Logistic回归模型;

(2) val lr = new LogisticRegression();

(3) .setMaxIter(100);

(4) .setElasticNetParam(0.0);

(5) .setRegParam(0.0);

(6) .setStandraize(false)。

然后,根据数据进行训练:

(1) //training 为训练集,test为测试集;

(2) val model = lr.fit(training).transform(test)。

即可获得原始数据经过Logistic回归的分类结果。获得的新数据结构如表3所示。

表3 LogisticRegression模型结构

在获得信息表后,就可以进行对应的域的划分。域的划分由损失函数决定,可以根据决策表中的每一个样本来选择合适的损失函数。根据定义,对于每一个对象,我们都可以构造损失函数,如表4所示。表4中,λi表示第i个对象的损失函数,具体定义由表1描述。

表4 损失函数的数据结构

αi和βi为由损失函数划定的阈值。其公式为

(4)

(5)

在Spark中,由Logistic回归得到的结果中包含很多参数,这里只使用计算得到的条件概率。根据条件概率Pr的划分,可以判断此对象为正例、反例或延迟决策。判断方法根据规则(P)～(N)得到:

综上所述,在整个决策过程中,决策粗糙集根据计算得到的三枝决策的阈值参数αi和βi,生成相应的决策规则。二元Logistic回归模型用来计算先验概率。在实际中,一般使用统一的损失函数而不是对每一个样本分别设定损失函数,这样会显著减少工作量;对于延迟决策的部分,可重复训练过程,尽可能获得更多的信息以帮助决策。

2.2 算法流程

基于Logistic回归的三枝决策算法流程如图3所示。

图3 基于Logistic回归的三枝决策算法流程示意

具体描述如下。

(1) 对于给定的问题选择相关的自变量和因变量,构造信息表。

(2) 使用二元Logistic回归建立回归方程。

(3) 根据二元Logistic回归方程,对每一个样本Ui,计算对应d=1的条件概率Pr[(d=1)|ui],d为样本状态。

(4) 根据三枝决策模型生成决策规则:对任意样本Ui(i=1,2,3,…,n),根据经验和其他信息,设定两个状态d=1和(d=1)时采取不同行动的损失函数,并由损失函数计算相关的阈值αi和βi。

(5) 确定每一个样本的最终决策。对于ui∈U,比较Pr((d=1)|ui)与αi和βi的大小关系。当Pr((d=1)|ui)≥α时,ui的接受状态为d=1;当β

(6) 对于延迟决策的部分,回到第2步继续整个算法,直到全部得到归类或到达设定的精度。

2.3 MapReduce 过程分析

由于整个程序是通过MapReduce模型实现并行化的,所以从MapReduce的角度来描述整个步骤更能体现程序是如何并行运行的。其整体运行流程如图4所示。

对于有N个特征的分类数据,其结构如表5所示。表5中,ωi表示第i个特征。

结合图4和表5,输入数据的结构为RDD 1。根据Spark文档对LogisticRegression模型的描述,所有的特征被描述为一个特征向量。所以,第1步,对RDD 1中的所有特征进行合并,使其成为一个向量,即通过第一次map,得到RDD 2。第2步,对RDD 2中的数据进行二元Logistic回归,得到表3描述结构的RDD 3。第3步,通过select方法在其中选出概率信息得到RDD 4。此时完成第一部分工作。

第4步,构建损失函数表。由于损失函数是提前设定的,所以可以从给出的损失函数表构建形式如表4的RDD 5。第5步,计算阈值αi与βi。根据式(4)和式(5)计算αi和βi得到RDD 6。第6步,通过join操作使RDD 6与RDD 4进行合并,得到的结果形式如RDD 7。最后,根据规则(P1i)～(N1i)即可得到最终的结果RDD 8。最终结果保存于prediction项中。

图4 MapReduce模型下的算法流程描述表5 输入数据结构

结构元素注释label标签ω1特征1ω2特征2︙ ︙ ωn特征n

3 实验与结果分析

在阿里云平台上搭建实验环境。使用3台阿里云通用计算型ecs.sn1ne.large服务器。服务器配置如表6所示。

表6 服务器配置

测试数据集来自UCI开放数据集,是一个常用的标准测试数据集,由加州大学欧文分校(University of California Irvine,UCI)提供。数据集均为分类任务。测试结果与结果分析如下。

3.1 Mushroom

Mushroom数据集包括伞菌和小伞菌属中23种假设样品的特征。每种物种都被确定为绝对可食用的、绝对有毒的,或具有未知的可食性且不被推荐。后一类与有毒类相结合。数据由逗号分隔,每一行定义了一个样本,包含可食、顶盖形状、顶盖光滑、顶盖颜色等共计22种特征。全部样本总计8 224条。使用三枝决策方法对数据集进行分析,采用二元LogisticRegression作为前置分类器,迭代100次,参数无正则化处理,无归一化处理。图5表示了整个数据集经过二元Logistic回归后的条件概率分布。其中,横坐标代表概率值区间,纵坐标代表区间内样本出现的频率。

图5 Mushroom数据集的条件概率分布

由图5可知,当进行100次迭代后,共有8 025条数据分布在区间(0,0.085)和(0.935,1)内。

然后,对不同的边界取值,以考察精度A与F1两个指标。其结果如图6所示。

图6 整体准确率指标

(6)

(7)

式中:m——总的样本个数;

I(·)——指示函数;

p,r——查准率和查全率。

由试验数据可知,对于本轮分类,从精度和F1指标考虑,主要受α的影响。即本轮的分类效果主要由划分到正域的样本个数决定。经过计算,在α=0.44时,其分类效果达到最好,三枝决策分类的精度要高于前置分类器的精度,且此时边界域较小。在分类过程中,边界域的大小同时影响本轮分类精度和下一轮的精度。由于精度和F1指标的定义都未考察负域划分的准确率,所以β取值的影响在图6中体现不明显。但显而易见的是,增加正域和负域的范围可以使边界域减小,从而在整体上减少分类的轮数,使分类效率提高。从试验结果可知,在选取合适的α和β的情况下,三枝决策算法能够通过后续的判断使得分类的精度较前置分类器有所提高。

3.2 connect-4

connect-4 数据集包含了所有符合游戏规则的8种位置。该数据集中两位玩家都还没有获得胜利,并且下一步棋完全不受干扰。‘x’表示玩家1,‘o’表示玩家2。最后的结果为玩家1本局的理论结果,分别为获胜(win)、失败(loss)、和局(draw)。

该问题是一个多分类问题。在处理多分类问题时,逻辑回归会分别计算3种分类的可能性,并取最高的可能性作为分类结果。针对本问题采用三枝决策方法,如果数据被划分到负域,那么只能说明有较强的信息表示该数据不属于此分类,但是依然无法判断数据的准确分类。由此,结合实际问题,本文取β=0,即不设定负域,只区分正域和边界域。图7展示了当α在[0,1]取值时分类性能的变化。

图7 不同的边界值对分类性能的影响

由图7可知,当α取[0.4,0.5]时,分类的精度有所提高且F1与前置分类器相当。相较于前置分类器,加入三枝决策后,在合适的边界域范围内,分类效果较前置分类器有所提升。在边界域选择不好的情况下,精度维持在原来的水平。虽然从精度和F1指标来看,在一定范围内,三枝决策的分类效果较前置分类器有所提高,但是无论边界域以何种方式划分,总有一部分正例被划分到边界域中。因此,就准确率而言,加入三枝决策算法后,其分类准确率较原始分类器有所下降。对于此问题可由多次迭代解决。因为随着分类轮数的增加,边界域中的元素总是在减少的。从总体来说,三枝决策的应用在保证结果精度没有降低时,增加了结果的可信度,减少了结果的风险性。

3.3 运行效率

将三枝决策算法引入Spark平台的目的是希望借由Spark提供的并行化算法和大数据处理能力,以增强三枝决策算法的运行效率,使其能够更好地适应海量数据的分析,增加三枝决策算法的实用性。经过前两个数据集的分析,分别统计程序在集群模式和单机模式时的运行时间,结果如图8所示。图8中,系列1表示集群模式耗时,系列2表示单机模式耗时。

由图8可知,随着数据量的增大和运算复杂程度上的增加,集群运行的高效逐渐体现。并且,借助Spark的MapReduce模型,在单机模式下,依然可以提高运行效率。对于本文使用的三枝决策算法,当数据量在10 000条以下时,由于集群之间的调度与通信原因,单机模式的运行速度要高于集群模式;当数据量大于10 000条时,集群的运算速度逐渐体现出优势,并且数据量越大,优势越明显;但在数据量较小的情况下,Spark处理集群调度占用的时间接近甚至超过数据本身运算的时间,此时,使用Spark进行数据处理并不能发挥集群运算本身的优势。

图8 集群模式与单机模式运行时间对比

事实上,对于mushroom数据集,其本身在一次分类后结果准确率已经超过90%,所以本文的试验分类过程只进行了一次。对于connect-4数据集,由于问题为多分类问题,使用逻辑回归本身的分类准确率并不高。所以,此项测试中,分类方法使用了前文所描述的多次多轮分类。

表7给出了不同轮数的三枝决策算法运行时间对比。由表7可知,运算流程复杂度的增加会使计算时间增加。因此,随着复杂度和数据量两方面的增长,基于Spark的三枝决策算法的效率优势会越来越明显。

表7不同轮数的三枝决策算法运行时间对比s

4 结 论

通过上述试验结果可以看到,在Spark上实现的三枝决策算法有以下两个方面的提高。

(1) 由图8和表7可知,分布式集群运行的三枝决策算法效率在数据量超过10 000的情况下较单机算法有所提高,且数据量越大,提高越明显。

(2) 在Spark系统上,运行效率的提高意味着相同时间内可以通过更多轮的训练,通过图6和图7的对比可知,使用三枝决策算法进行分类,分类的性能较前置分类器略有提高。