燃料价格及电力需求不确定下电力生产决策的鲁棒优化

汪 建, 王 挺,2, 刘惠霞

(1.上海大学管理学院,上海200444;2.庆应义塾大学管理工程系,横滨2238522,日本;3.戴尔(中国)有限公司上海分公司,上海200050)

供应链不确定性问题一直是供应链管理中的一个重要研究问题.对许多供应链而言,供应链管理和决策的挑战主要来自于各种影响因素的不确定性.电力工业是国民经济发展中的基础能源产业,因而如何应对外界因素的不确定性,保证整体电力供应链的稳定尤为重要.

随着电力体制的改革,传统的垂直一体化的电力模式逐步改变,形成了由发电、输电、配电和电能销售几个环节组成的电力供应链,并因此造成了供应链供需两侧面临更大的不确定性.与其他产品不同,电力是国民经济发展不可或缺的部分.电力供应决策不仅要考虑成本的最优,还要考虑电力供给的稳定性.因此,发电企业将更加重视实施鲁棒性能的发电策略,以期降低风险,保障民生.

针对不确定环境下的供应链运作问题已进行了大量的研究.刘英等[1]对随机需求条件下的供应链采购决策进行了探讨.邱若臻等[2]研究了需求概率分布不确定条件下的多市场鲁棒优化问题.张克勇等[3]研究了随机需求下的供应链定价延迟策略.彭红军等[4],Fang等[5]分别研究了供应不确定性下的供应链均衡供应决策问题和供应链竞争问题等.

与其他产品不同,电力供应链供需两侧的不确定性主要受燃料价格、电力需求、风电、电价等因素的影响.Meza等[6]考虑了燃料价格不确定下的电力系统电力扩张问题.Roh等[7]考虑了电力需求不确定下的输发电规划问题.Malcolm等[8]提出了电力分配模型,并基于场景鲁棒优化的方法研究了电力需求不确定的情形.针对风电的不确定性,雷宇等[9]和Liu等[10]分别对含风电系统机组组合优化问题以及风电场最大装机容量问题进行了研究.其他电力系统中的不确定性还包括电力市场中电价的不确定性[11-15].已有研究在考虑电力供应链的不确定性的影响时仅考虑了单个因素的不确定性,仅有部分研究涉及多种因素的不确定性影响.Lopez等[16]考虑了需求、发电量的不确定性.鞠平等[17]考虑了需求、投资、电价的不确定性.Wang等[18]考虑了燃料价格和电力需求的不确定性.上述研究在建模过程中都是对影响因素进行单独建模,而未考虑各影响因素之间的交互作用对电力系统的影响.

在研究方法上,为应对供应链决策领域的不确定性,主要采用随机规划方法[6-7,9,11,16]、模糊优化方法[12,17]以及鲁棒优化方法.考虑到随机规划方法和模糊优化方法在使用过程中需要通过有限的数据样本以及决策者个人经验来确定不确定性的概率分布函数或模糊隶属度函数,往往带有较大误差或主观随意性[19],因而并不能如实反映供应链中面临的不确定性.

鲁棒优化方法作为处理供应链不确定性问题的一种新的优化方法,能解决内部结构(如参数)和外部环境(如扰动)的不确定性[20],对模型中含有不确定数据,或者仅仅知道其属于某一个不确定区域的优化问题都能有较好的处理[21-22],其最优解对不确定集合内的任意元素都保证约束可行性.通常,根据不确定集选取类型的不同,鲁棒优化方法可分为场景鲁棒优化方法[8]、盒式鲁棒优化方法[23]和椭球鲁棒优化方法[24].目前,已有使用鲁棒优化方法解决电力系统中不确定性问题的研究.Malcolm等[8]应用场景鲁棒优化方法来处理电力需求的不确定性.Liu等[10]基于盒式鲁棒优化方法对风电场的不确定性进行了研究.童小娇等[13]应用盒式鲁棒优化方法研究了自发电计划.Wang等[18]基于电力分配基本模型,分析了燃料价格属于椭球不确定集下的最优决策等.

本工作借鉴相关研究成果,并在文献[8]建立的需求不确定条件下的电力分配模型基础上,构建了燃料价格和电力需求同时不确定,并且两个影响因素相互关联的电力生产鲁棒优化模型,研究内容主要包括以下3点.

(1)本工作研究了发电侧燃料价格和需求侧电力需求二者的不确定性,同时考虑了两个影响因素相互关联情况下的电力生产模型.而已有的研究[8,18]往往只考虑了单个因素的不确定性影响,或者考虑了多个因素但因素之间是相互独立的情况,鲜有二者兼顾.

(2)在研究方法上,本工作应用椭球不确定集描述燃料价格和电力需求的不确定性.已有的研究多使用场景鲁棒优化方法[8]或者盒式鲁棒优化方法[10,13]来处理电力系统的不确定问题.相对于场景鲁棒优化方法和盒式鲁棒优化方法,椭球鲁棒优化方法更为复杂,计算量大且求解更加困难,但对不确定参数的涵盖半径及分布离散程度可以进行有效控制,能实现解的保守性与最优性相协调的最优决策[18].

(3)在所建模型具有鲁棒性的基础上,本工作进一步研究了影响因素的不确定范围与目标值总成本之间的关系,并分析了燃料价格和电力需求这两个参数的不确定范围对总成本的影响显著性,而已有的研究往往只针对所建模型的鲁棒性能.

本工作将为电力生产决策准确刻画不确定因素带来的影响,有效利用不确定因素的信息为电力部门制定安全经济的决策方案提供理论依据.

1 电力生产决策基本模型

1.1 基本模型描述

本工作考虑了一个由发电企业和终端用户电力需求所构成的电力供应链系统.发电企业生产电力输送到需求端以满足不同的终端用户电力需求,模型框架如图1所示.通常的电力供应链中同时有多个电力来源以保证电力输出的稳定性;而在需求侧,电力的需求受到季节、气候等因素的影响不断变化.在本工作中只考虑两种电力负荷模式,即波峰与波谷模式.图2是按照降级重新排列后的实时负荷图.在负荷持续模型中,采用阶跃函数表达各个负荷模式(如波峰、波谷等)下的电力需求,并假定各个负荷模式下的需求是稳定的.

图1 电力分配模型Fig.1 Electric power allocation model

图2 分段线性负荷持续模型Fig.2 A linear model on power loads in different periods

1.2 模型变量参数

(1)k表示某个发电厂(k=1,2,···k),并设有限集合K,使k∈K.

(2)l表示某种电力负荷模式,在本工作中主要包括波峰模式(l=1)和波谷模式(l=2).

(3)xk表示第k个发电厂的发电量.

(4)dl表示电力负荷模式l下的电力需求.

(5)ykl表示第k个发电厂分配给电力负荷模式l下的电量.

(6)pl表示电力负荷模式l下的累积负荷.

(7)tl表示电力负荷模式l下的持续时间.

(8)ck表示第k个发电厂运营所产生的固定成本.

(9)fk表示第k个发电厂运营所产生的可变成本.

1.3 电力生产决策基本模型

基于电力分配模型以及分段线性负荷持续模型,提出如下的以发电企业的发电总成本最小化为目标的电力生产决策基本模型:

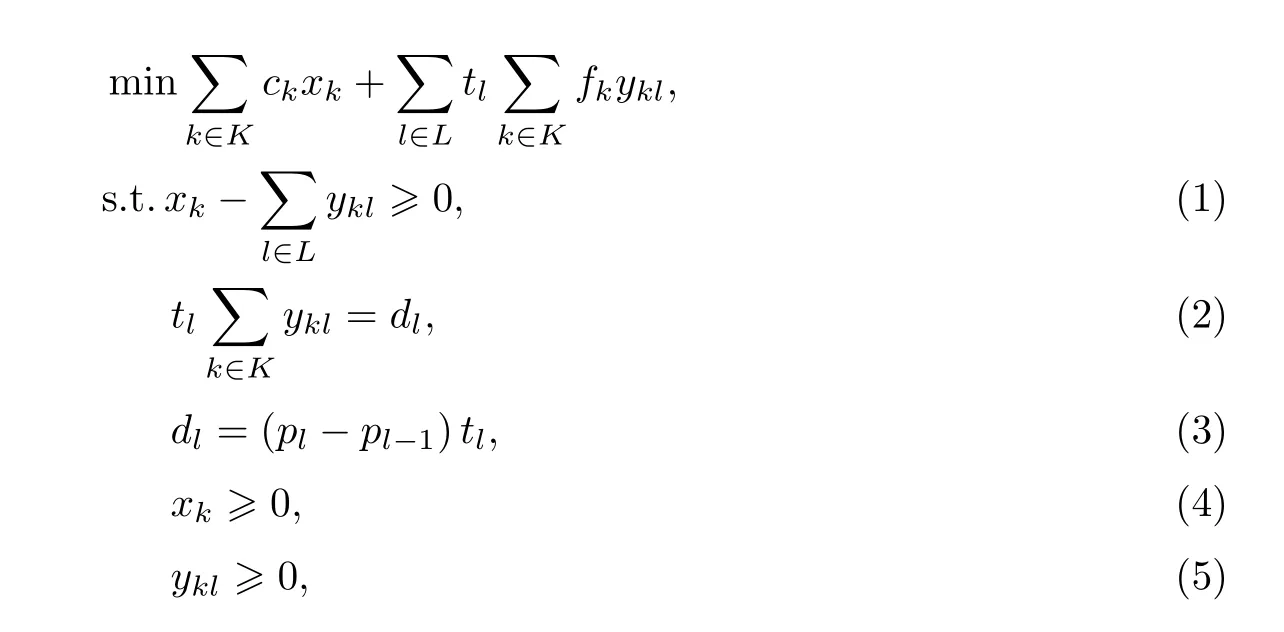
2 电力生产决策的鲁棒优化模型

2.1 椭球不确定集下电力生产决策的鲁棒优化模型

对于线性规划,Ben-Tal等[25]给出了其参数属于椭球不确定集下的鲁棒问题,并证明了不确定线性优化问题可以转化成为数据确定的二阶锥优化问题(second-order cone programming,SOCP).

定理1 考虑线性规划

式中,x∈Rn为决策变量,c∈Rn,A∈Rm×n,b∈Rm为给定的参数.记A的第i个行向量为,并假定P0k∈Rn×n,Pi∈R(n+1)×n为给定的不确定范围变化.令

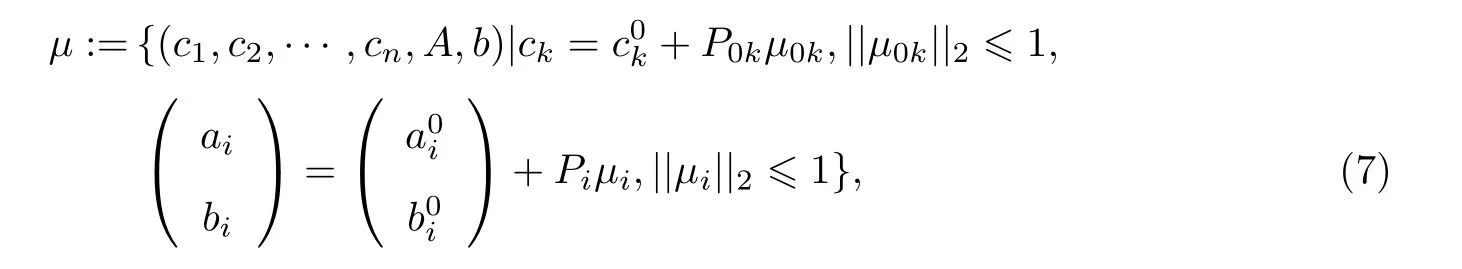
如此,原问题所对应得鲁棒问题可转化为如下的二阶锥规划:

式中,s表示约束松弛变量.

通过设定参数燃料价格f和电力需求d属于椭球不确定集,将电力生产决策的基本模型转化成如下对应的椭球鲁棒优化模型:

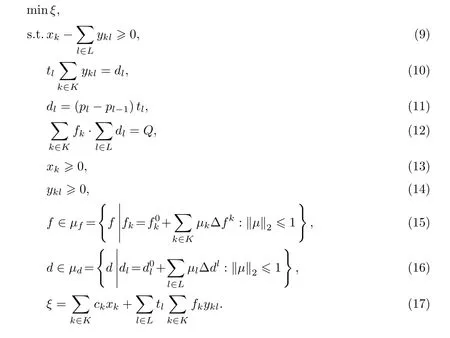
在电力行业中,燃料价格与电力需求之间存在相关性.石油等发电用燃料价格的上涨会造成发电成本的增加,导致电价上涨,用户会有节电意识,刺激电力使用量下降.在电力消费上,高电价会降低电力使用量,低电价会刺激电力使用量.本工作假设电价与燃料价格呈线性正相关,建立如约束(12)所示的燃料价格f和电力需求d的反比例关系模型,并设定二者的乘积为一个常数Q.

2.2 椭球鲁棒优化求解算法设计

目前,已有相当数量的算法可对二阶锥规划问题进行求解,主要包括内点法和重构算法等,还有较多可利用的软件,包括SeDuMi,SDPA和LMI工具箱等.各个软件的适用背景可参照文献[26].本工作依据定理1的求解思路,调用MATLAB中的SeDuMi工具箱进行求解,具体算法实现步骤如下.??

步骤1 设定初始值,设置遗憾值限定系数ω,并定义不确定参数初始值为f0,d0,有f0>0,d0>0,k=0.

步骤2 计算模型的可行解ξ(x),调用SeDuMi工具箱计算模型可行解,当且仅当6ω成立时,输出模型的解.??

步骤3 设置不确定参数的扰动方向 ∆fk,∆dk.

步骤4 计算参数不确定范围,设不确定?参数的步?长为?ωf,ωd,有fk+ωf∆fk?>0,dl+ωd∆dl>0,则参数不确定范围变动计算为fk+1,dl+1=fk+ωf∆fk,dl+ωd∆dl.

步骤5 令k=k+1,返回步骤2.

关于参数燃料价格和电力需求扰动方向的解释如图3和4所示.在椭球鲁棒优化方法中,参数的不确定范围大小由其步长来设定,通常有2种情况:①各不确定性因素的扰动方向一致,即各参数的不确定范围和椭球形状成比例,不确定范围的步长ω成比例(见图3);②各不确定性因素的扰动方向不一致,即各参数的不确定范围不同,不确定范围的步长ω也不成比例(见图4).

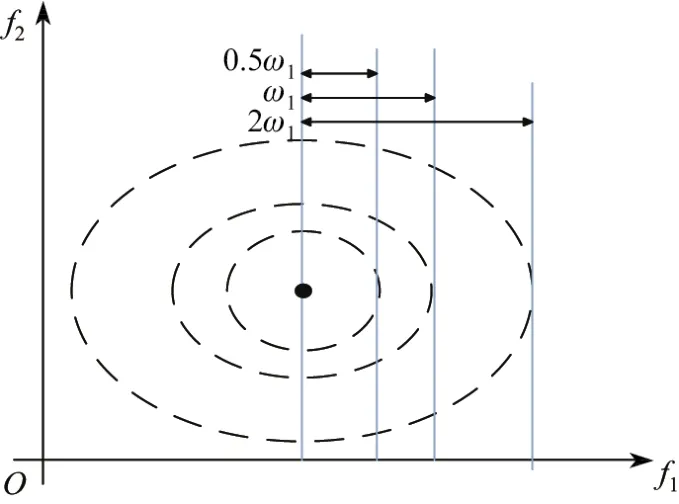
图3 各不确定性因素的扰动方向一致Fig.3 Disturbance directions of diff erent uncertainty factors are consistent

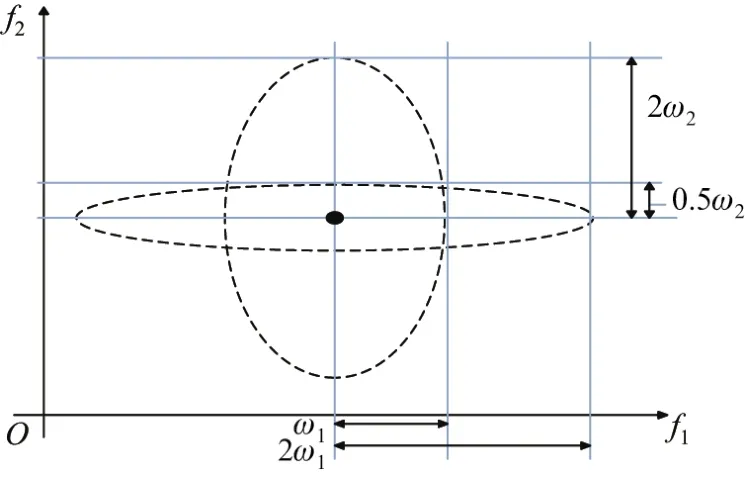
图4 各不确定性因素的扰动方向不一致Fig.4 Disturbance directions of different uncertainty factors are inconsistent

3 仿真与分析

根据本算法设计,针对不确定性因素的两种扰动方式,通过MATLAB编程,SOCP优化软件采用SeDuMi 1 1R3,在Inter Pentium P6000,CPU 1.87 GHz,1 GB内存,Windows 7的主机上运行,对电力生产决策的鲁棒优化模型进行仿真分析.具体参数设置如下:参与电力供应链有3个发电企业,即电力工厂k为1,2,3;2种负荷模式分别为l=1(波峰)与l=2(波谷),具体参数取值如表1所示,其中序号5代表发电厂运营产生的固定成本为0,即任何电力的生产是即时生产,没有任何外部设施,是一种极值理想状态.设定不确定范围步长ω的值,分别为ωf1=5,ωf2=2.5,ωf3=10,ωd1=1,ωd2=6.

表1 参数取值初始值Table 1 Initial values of the parameters

根据影响因素不同的扰动方向,分情况讨论数值实验结果.

(1)当参数f和d的扰动方向一致时,即fk和dl的不确定范围都成比例变化时,参数f1,f2,f3和参数d1,d2的不确定范围比例是一样的.设定Q=31 000,其变化步长分别按照比例在0.5∼8倍之间以0.1的步长增长进行实验,得到76组解.由于实验结果较多,并且不确定范围和总成本之间基本成线性关系,因此,本工作选取4种不同比例大小的步长,分别取值为(0.5ω,ω,2ω,4ω)的解,即各参数的不确定范围如下: ①[fk−0.5ωfk,fk+0.5ωfk];②[fk− ωfk,fk+ωfk];③[fk−2ωfk,fk+2ωfk];④[fk−4ωfk,fk+4ωfk];⑤[dl−0.5ωdl,dl+0.5ωdl];⑥[dl−ωdl,dl+ωdl];⑦[dl−2ωdl,dl+2ωdl];⑧[dl−4ωdl,dl+4ωdl].得出的实验数据结果如表2所示.

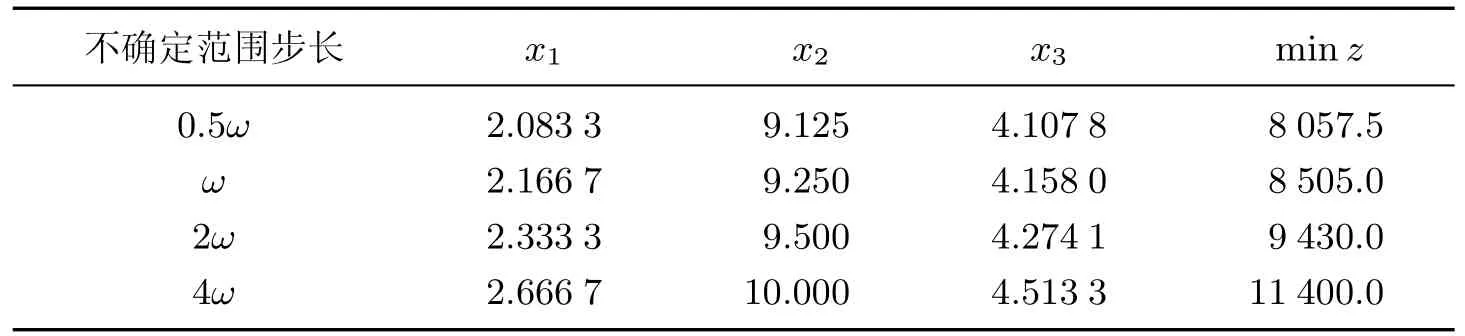
表2 不确定范围成比例时的解Table 2 Solutions when the parameter uncertainty ranges change with a fix ratio

分析表2可知,当不确定范围的步长在0.5∼2倍之间时,最优解(x1,x2,x3)近似等于(2,9,4),即模型的解具有鲁棒性.在外界环境不确定参数波动较小时,可直接取这个解为最优解.随着不确定范围步长ω的变大,参数的不确定范围增大,发电总成本随之增加,参数不确定范围与总成本的关系几乎是线性关系,满足min z=925k+7 680(其中k是不确定范围步长的倍数,k=0.5,1,2,4,见图5).

图5 不确定范围与总成本关系图Fig.5 Relationship between parameter uncertainty ranges and total costs

(2)当参数f和d的扰动方向不一致,fk和dl的不确定范围各自成同比例变化,f1,f2,f3的不确定范围步长比例相同,参数d1和d2的不确定范围步长比例相同时,设定Q=31 000,并使参数f和d的不确定范围变化步长分别按照比例在0.5∼8倍之间以0.1的步长增长进行实验,得到25组不同范围下的解,具体如表3所示.

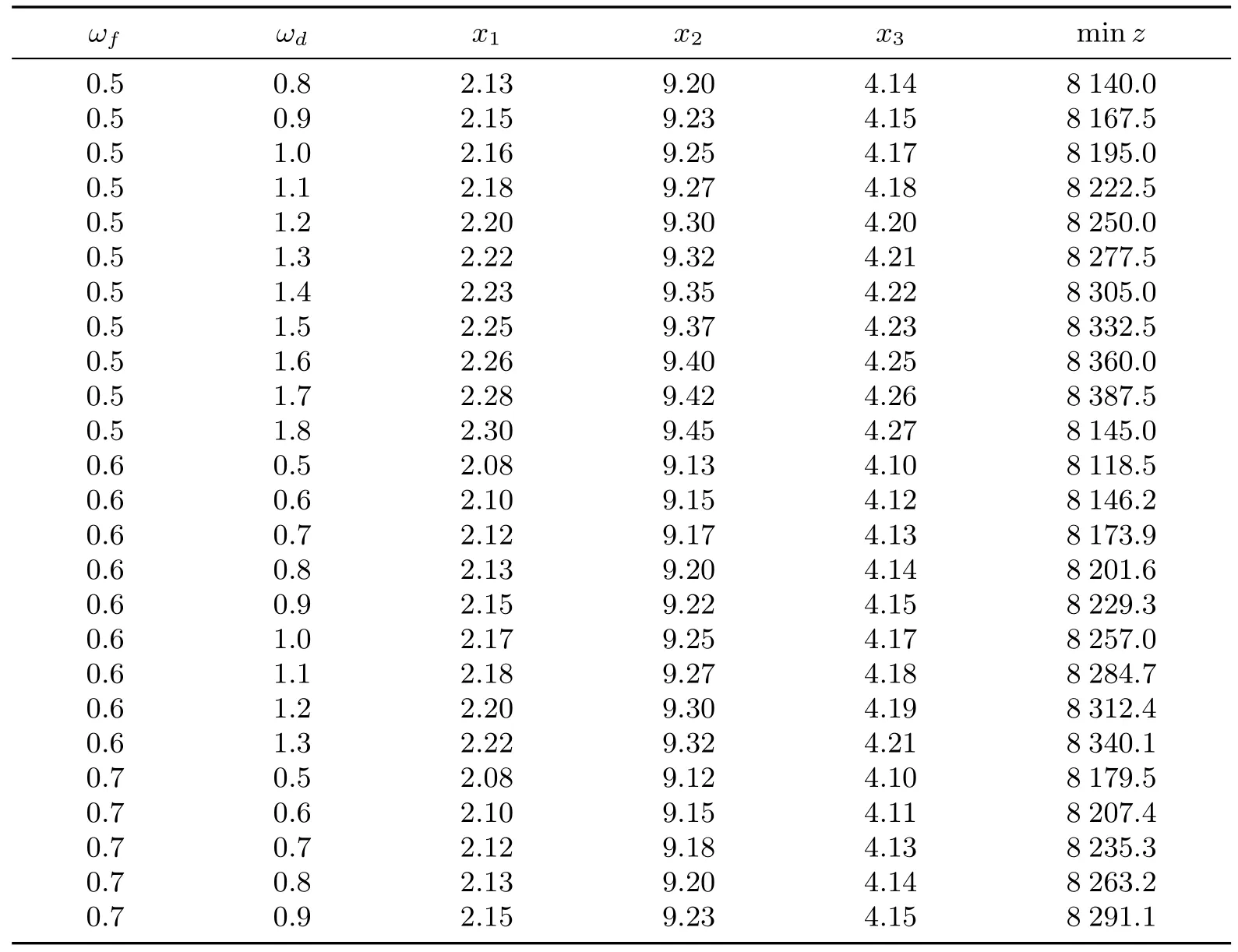
表3 不确定范围各自成比例时的解Table 3 Solutions when the parameter uncertainty ranges change with diff erent steps

分析表3可知,当参数的波动范围较小时,即ωf在0.5∼0.7之间,ωd在0.6∼1.8倍之间变动,最优解近似为(x1,x2,x3)=(2,9,4).这说明当燃料价格和电力需求的波动较小时,其最优解保持不变,模型的解具有鲁棒性,能应对外界的不确定性波动.进一步分析了不确定范围与目标值之间的关系,通过MATLAB编程得到了一个三维图像(见图6).

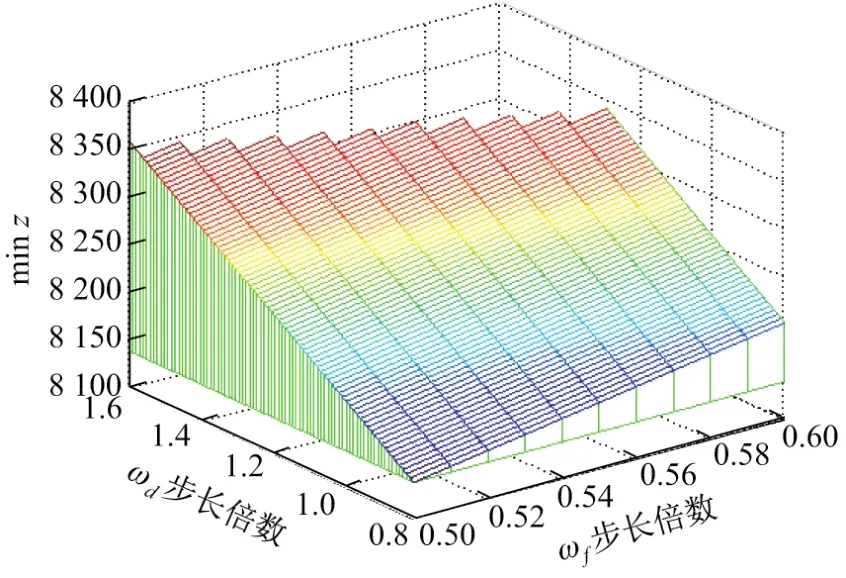
图6 不确定范围与总成本趋势图Fig.6 Trends of parameter uncertainty ranges and total costs

分析图6可知,x轴代表参数f的不确定范围变化步长的倍数,y轴代表参数d的不确定范围变化步长的倍数,z轴为目标函数值,即最小总成本.随着f和d的不确定范围变化步长的增大,即参数不确定范围的增大,总成本增加,但是总成本的增加并不与f和d的不确定范围呈线性关系.

综合分析表2和表3,比较了不确定性因素两种扰动方向时发现,当参数波动较小时,虽然其不确定范围的大小是不同的,但最优解可以相同,这和鲁棒优化的建模思想一致.鲁棒优化是考虑最坏情况下,在给定的不确定参数变化集合内,不确定参数的变化也能保证优化方案的可行性,因此验证了本模型的解具有鲁棒性.进一步分析发现,随着参数不确定范围的增大,目标函数值随之变大,并且当不确定性因素的扰动方向一致时,最小总成本与不确定参数范围的变化步长呈线性关系;当不确定性因素的扰动方向不一致时,最小总成本随参数不确定性扰动的增大而增加,但不呈线性关系.

为更准确刻画外界不确定性因素给电力生产决策带来的影响,进一步分析燃料价格和电力需求的波动范围对总成本的影响显著性,本工作通过大量数值实验,得到了不同Q值(Q1=143 400,Q2=155 880,Q3=163 300)下变量的不确定范围变动对总成本的影响显著性.假设不确定性因素的扰动方向各自一致,即fk和dl的不确定性范围各自成同比例变化,分别进行数值实验,结果如表4所示.

分 析 表4可 知, 当 参 数f和d的 不 确 定 范 围 分 别 为[fk−22ωfk,fk+22ωfk]和[dl−8ωdl,dl+8ωdl],即当Q1=143 400时,参数不确定范围的变化步长分别按照比例在0.5∼22倍之间以0.1的步长增长和在0.5∼8倍之间以0.1的步长增长进行实验.燃料价格和电力需求发生了同样大小的扰动,即参数不确定范围的变化步长发生0.1的变化,燃料价格带来的发电企业总成本的效应为∆Zf=?Zf+−Zf−?=25 560.3−25 489.5=70.8,电力需求带来的发电企业总成本的效应为∆Zd=(Zd+−Zd−)=25 555.7−25 489.5=66.2.相比于燃料价格的波动,目标值对电力需求的扰动不敏感,电力生产决策的制定过程中应尽可能关注燃料价格的不确定性,并通过增加化石燃料的储备等措施来应对燃料价格的波动.

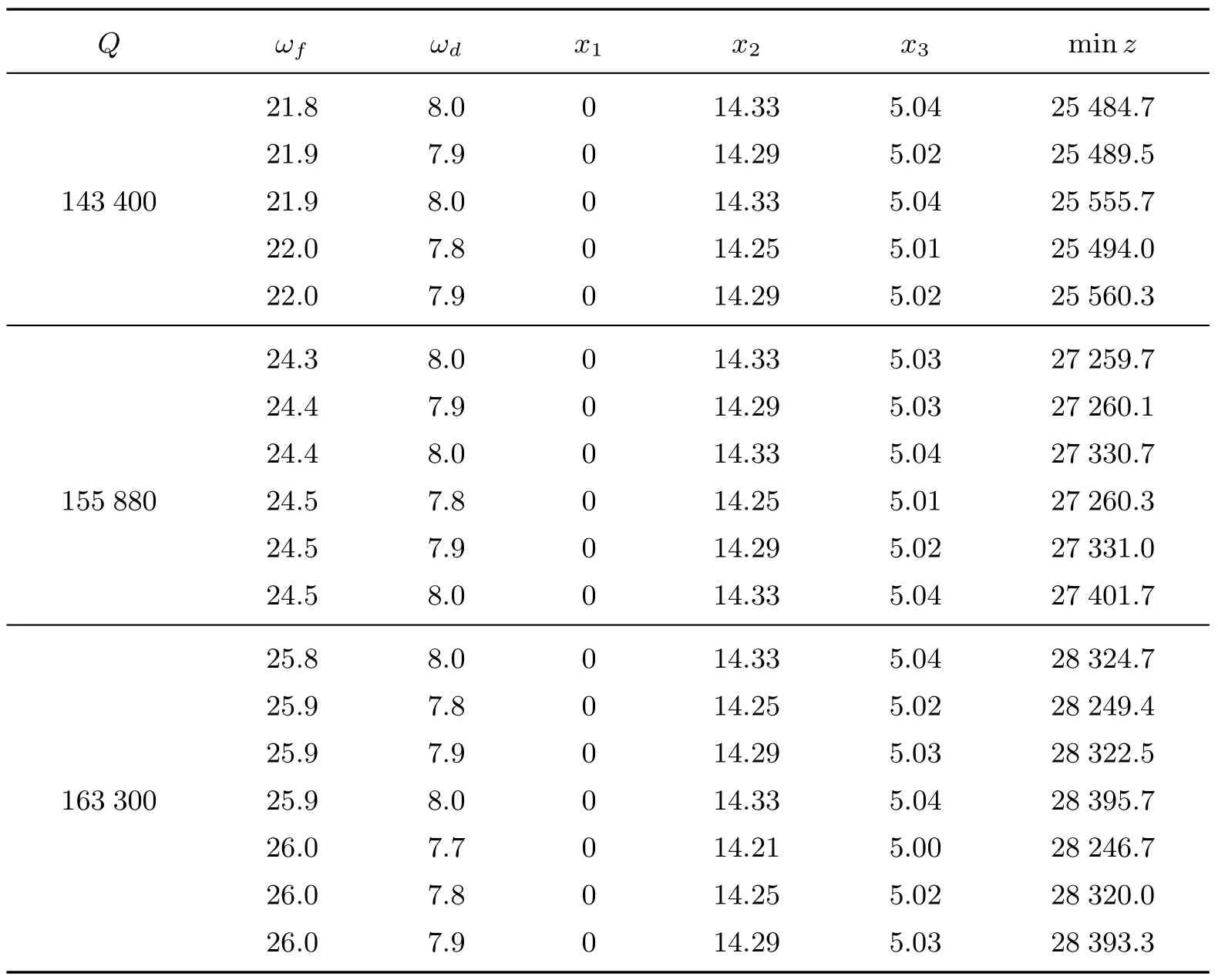
表4 不同电力市场发展程度Q值下的解Table 4 Solutions under diff erent development degree Q in electric power market

当参数f和d的不确定范围分别为[fk−24.5ωfk,fk+24.5ωfk]和[dl− 8ωdl,dl+8ωdl],即当Q2=155 880时,f和d发生同样大小的扰动,燃料价格变动带来的发电企业总成本的效应为∆Zf=?Zf+−Zf−?=27 331.0−27 260.1=70.9,电力需求变动带来的发电企业总成本的效应为∆Zd=(Zd+−Zd−)=27 330.7−27 260.1=70.6.燃料价格和电力需求的波动所产生的对总成本的效应几乎相等,说明目标值对于燃料价格和电力需求的扰动同样敏感.据此定义参数f和d的不确定范围[fk−24.5ωfk,fk+24.5ωfk]和[dl−8ωdl,dl+8ωdl]为临界范围.

当参数f和d的不确定范围分别为[fk−26ωfk,fk+26ωfk]和[dl− 8ωdl,dl+8ωdl],即当Q3=163 300时,f和d发生同样大小的扰动,燃料价格变动带来的发电企业总成本的效应为∆Zf=?Zf+−Zf−?=28 320.0−28 249.4=70.6,电力需求变动带来的发电企业总成本的效应为∆Zd=(Zd+−Zd−)=28 322.5−28 249.4=73.1.目标值对于电力需求更为敏感,在电力生产决策制定过程中应重点关注用户电力需求信息,调整电力生产以减少电力需求波动给企业带来的影响.

4 结束语

不确定性贯穿在电力供应链运作的整个过程中,如何处理这些因素的不确定性对电力供应链决策的影响是供应链管理中不可忽略的问题.本工作建立了关于发电企业的电力生产决策的鲁棒优化模型,通过数值实验,验证了本算法的可行性,并得到了参数不同扰动方向情况下的实验结果,得到以下主要结论.

(1)当燃料价格和电力需求这两个参数的波动较小时,模型的最优解近似相等,即所得出的解具有鲁棒性,所制定的电力生产决策能应对外界不确定性.随着参数不确定范围的增大,总成本增加.当不确定性因素燃料价格和电力需求的扰动方向一致时,总成本随着参数不确定范围的增大呈近似线性增加.当不确定性因素燃料价格和电力需求的扰动方向不一致时,总成本随着参数的波动加剧而增加,但并不呈线性关系.

(2)通过分析燃料价格和电力需求这两个参数的不确定范围对总成本的影响显著性,发现随着参数变动范围的差异,燃料价格和电力需求的不确定性对于电力生产决策影响的显著性也不一样.在本工作中,当燃料价格f的变动范围为[fk−24.5ωfk,fk+24.5ωfk],电力需求d的变动范围为[dl−8ωdl,dl+8ωdl],即当Q2=155 880时,燃料价格和电力需求对发电企业总成本的影响大致相等.通过大量实验发现,当参数的不确定范围小于这个范围时,燃料价格对发电企业的总成本影响更大,在制定决策的过程中应尽可能避免燃料价格带来的不确定性.当参数的不确定范围大于这个范围时,电力需求对发电企业的总成本影响更大,在电力生产决策制定过程中应重点关注电力需求的波动,并制定有效的应对策略以减少电力需求的影响.

本工作为不确定性电力供应链的决策问题提供了理论支持及相关的方法.研究结果表明,所建立的模型和算法能有效描述燃料价格和电力需求等影响因素的不确定范围对于电力生产决策的影响.研究结果可以为电力部门制定安全经济的决策方案提供理论依据.