GPS在高铁控制测量中的精度分析——以西成高铁为例

夏海宁，张帆宇扬，袁德宝，王 杰，庞世晨

(1. 廊坊市水利勘察规划设计院,河北 廊坊 065000； 2. 中国矿业大学(北京)地球科学与测绘工程学院,北京 100083； 3. 沧州水利勘测设计院,河北 沧州 061000； 4. 廊坊市禹达勘测设计有限公司,河北 廊坊 065000)

随着我国高铁技术的不断成熟[1]，越来越多的城市间依靠高铁变的紧密起来，但西安与成都之间由于地形地貌复杂，给西城高铁的建设带来了很大挑战。与其他高铁线路相比，西成高铁需要穿越秦岭和大巴山区等地质地貌条件极为复杂的区域。线路主要由桥梁和隧道连接，超过10 km的特长隧道共有7座，最长的秦岭天华山双线隧道，距离超过15 km[2]，路线中隧道较多，其中密集隧道群长度达到了110 km，在工程西段、汉中境内和秦岭山区的桥隧比分别高达92.1%、95%、94%，可以说整条高铁线基本上是靠桥梁和隧道连接起来的。同时西成高铁首次采用长达47 km、25‰的大坡度设计[3]，如此长距离、大跨度的桥隧工程线路是我国最具山区特点的高标准现代化高铁建设项目，因此如何在险峻复杂山区为修建高速铁路进行高精度的控制测量是保证高铁顺利建设的关键性问题。

1 高铁控制测量

1.1 试验区介绍

本文试验区选择在整条西成高铁[4]中地质地貌复杂、具有代表性，且为全线设计建设的难点和重点区域的陕西境内的西安至陕川县标段，技术设计书要求分CP0、CPⅠ和CPⅡ三级进行布设，CPⅠ网采用CP0点成果进行约束，CPⅡ网采用CPⅠ点成果进行约束，起讫里程为DK0+000～DK343+900，沿设计线路两侧带状分布，实际可用CPⅠ点8个。本次复测工作对CPⅠ级控制点采用同级校检，由于CP点沿设计线路带状分布，为加强三角网网型强度，提高解算数据精度，需在远离线路的合适位置架设辅助点。

1.2 控制测量的意义

由于西成高铁施工测量环境复杂，受限于观测条件，测量时不可避免地会产生误差，因此需要在合适的地质地貌区域选择稳固的点作为控制点。若干个控制点构成符合几何条件的控制网型，作为西成高铁在西安至陕川县标段测区测量的骨架，控制累积误差到限差范围内。由于不同网型结构的测量精度、稳定性及成本不同，因此设计出合适的网型至关重要。

1.3 数据来源及质量

本文选择西成高铁CPⅠ点复测5月7日同步观测数据进行GNSS网型布网设计分析。

外业观测时，选取8台双频Trimble GPS接收机，该款双频接收机具有优于5 mm+2×10-6D等级的静态定位标称精度。严格按照《全球定位系统(GPS)测量规范》(GB/T 18314—2009)中E级网规范，针对CP点的复测要求，外业观测时段定为2 h，保持开关机同步、同步观测同一卫星组。

西安至陕川界共分为10个投影带[5-7]，本次试验复测的CP点采用平面坐标系统，按高斯投影的方法建立工程独立坐标系，投影分带以按照对应的西成高铁路线每千米平均高程变形值小于或等于10 mm的标准进行设计。

2 基线向量设计及解算

2.1 GNSS基线向量网的设计原则

卫星间同步测量不要求通视[8]，其测量得到的点位精度与所布设的几何网型有很大关系。GNSS网的图形设计[9-11]需要在考虑工程项目需求、成本预算、施工时长、GNSS接收机类型等条件的同时，也要保证测站点交通便利、有足够的重复设站数等。

2.2 GPS网基线向量的解算

GPS网基线向量采用三差模型法求解，三差是不同历元同一组卫星的双差之差，三差方程消除了模糊度参数，并且进一步削弱了卫星轨道误差和大气折射误差。

2.2.1 三差法解算函数模型

利用三差法来解算函数，能够消除卫星定位中的多数误差影响因素，获得更为精确稳定的测量结果。设测站1、2分别在t1、t2观测历元同步观测了编号为p、q的卫星，根据双差观测方程求差，得三差模型

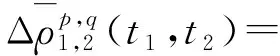
(1)

式中

2.2.2 三差法解算随机模型

设某观测历元t1同步观测卫星数为n，则可将基准站T1、测站T2至各卫星的非差相位观测值先验方差定义为

(2)

式中，a、b为常数；E为相应站点的卫星高度角。

假设不同卫星与测站之间的相位观测值不具有相关性，同时历元间的双差观测值不相关。因此可以通过误差传播定律[12]，在ti观测历元双差相位观测值的方差-协方差矩阵(式(3))的基础上，获得三差法解算的随机模型(式(4))。

(3)

式中,⊙为克罗内克积；ln-1表示n-1维元素均为1的列向量；In-1为n-1阶单位矩阵。

(4)

3 GPS网布设方案及布网特点

在本文试验方案中，采用了以下4种网型设计进行分析试验，其平差综合情况见表1。

方案Ⅰ：全面网结构。所有测量的基线向量均参与网平差[13]，其布网方案如图1所示。

图1 全网式示意图

方案Ⅱ：边连式结构。选择部分基线向量参与网平差，依靠共用的基线相联系。由于其有较多的复测边和非同步图形闭合条件[14-15]，故而在其余条件相同的情况下，该网型需观测的时段数较另外3种网型有所增多，网型可靠性较高，其布网方案如图2所示。

图2 边连式示意图

方案Ⅲ：点连式结构。选择部分基线向量参与网平差，只靠一个点连接，不具有较高的几何强度，在工程实践中也很少单独使用，其布网方案如图3所示。

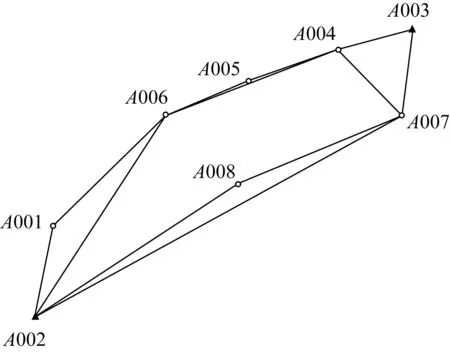
图3 点连式示意图

方案Ⅳ：导线网结构。根据实际情况，选择部分基线向量参与网平差，利用边连式与点连式两种布网方式的特点，将两者结合起来。该网型呈封闭状，边网混合使其不仅几何强度较高，而且减少了外业工作量，在工程测量中有着较多的应用，其布网方案如图4所示。

图4 边网式示意图

方案基线数量相对闭合差最大值(×10-6)闭合环最大节点数相对闭合差最小值(×10-6)闭合差最小值/mm闭合差最大值/mm方案Ⅰ260.428037.51409.476688.6466方案Ⅱ140.629036.48308.809973.0143方案Ⅲ121.490034.233011.919476.2584方案Ⅳ81.223232.13908.265050.5653

4 高铁CPⅠ的复测结果分析

4.1 平面控制GPS测量精度指标及限差

(1)平面控制GPS测量的精度指标见表2。

(2)CPⅠ、CPⅡ复测的结果与相应的设计指标的坐标差值需满足下列规定(见表3)。

此外，选取满足要求的基线观测值进行平差计算，由于国内测绘行业数据平差处理的规范标准要求，本试验采用科傻平差软件进行平差处理，观测数据记录和计算成果取位满足相应的技术要求。

表2 GPS测量控制网的主要技术指标

表3 CPⅠ、CPⅡ控制点复测坐标较差及相对精度限差[18]

4.2 基线平差处理后的点位精度分析

以方案Ⅰ全面网的平差结果作为最或然值，将其他方案平差结果分别与方案Ⅰ的平差结果从水平方向进行点位坐标较差精度对比分析。

复测结果点位差值如图5所示。

图5 控制点复测点位差值

图5中用到的计算公式有

(5)

式中，ds为点位差值。

(6)

从图5中可以看出，方案Ⅳ边网式布网结构与方案Ⅰ全面网结构平差处理得到的点位坐标较为接近，方案Ⅱ边连式布网结构解算得到的点位坐标与方案Ⅰ全面网结构之间较差在0.4～7.9 mm之间，而方案Ⅲ点连式布网结构得到的较差在0.3～6.2 mm之间。

相邻点坐标差之差相对精度要求为1/130 000[19]，控制点复测坐标较差不超过20 mm。由以上数据分析可知，方案Ⅰ、Ⅱ、Ⅲ、Ⅳ均能够满足CPⅠ的精度要求。

4.3 基线平差处理的最弱点边精度对比

由表4、表5可以看出，方案Ⅰ全面网的平差结果最优，方案Ⅳ导线网次之，方案Ⅱ边线网与方案Ⅲ点连式的精度稍低，但以上4种布网方案均能够满足1/180 000的限差要求。

表4 平差处理后的最弱点精度

表5 平差处理后的最弱边精度

5 结 语

本文以西城高铁为例，利用GPS接收机所采集的数据，通过三差模型法对数据进行处理，分析了4种不同GNSS布网结构的CPⅠ控制点复测网平差解算成果，并采取多种不同的指标进行对比分析，可知GNSS网精度和可靠性的主要因素是基线向量的观测精度。在小区域工程测量中，如果人员和仪器有限制，地质地貌环境不允许，可以考虑使用方案Ⅳ边网式布网结构，适当减少重测点数，也能满足精度要求，同时，在对采集到的数据进行内业处理时，可以剔除不满足精度要求的基线，构成混连式布网构型或边连式进项平差，以得到理想精度。