基于屈服接近度的基坑安全性评价方法研究

郭树勋， 郑世杰， 王金满， 杨 锐， 郑 帅， 姜谙男， 孔汇川

(1. 中交隧道工程局有限公司， 北京 100102； 2. 大连海事大学交通运输工程学院, 辽宁 大连 116026)

0 引言

对周边土体安全性评价是基坑施工过程安全有序进行的理论保证[1-2]。传统的评价方法多是采用岩土稳定性分类分区、数值计算塑性区分布等方法进行判断，通过强度分析及相应的强度判据对岩土体的破坏机制和支护设计进行研究指导[3-6]； 但是，这种以单轴抗拉、抗压强度作为安全性评价指标的经典材料力学方法无法对处于复杂应力状态下、具有强烈变异性的地下工程周边土体形成有效的施工风险评价。

基坑施工过程中，部分存在危险的区域未进入塑性状态，因而无法通过经典的分级理论对其进行提前示警预测。为了解决这个问题，一些学者进行了不同研究方法的探究。张俊文等[7]从点的安全系数角度综合评价了多层次堆积体的稳定性及破坏模式,并给出了有效的加固建议; 马春景等[8]通过单元状态指标的形式，对流固耦合作用下岩土工程稳定性变化过程进行模拟计算； 周辉等[9]根据围岩中接近屈服面区域安全程度的差异，对非塑性区的危险程度进行研究，在经典塑性理论框架内定义了屈服接近度指标，并建立了相应于各种不同类型的屈服准则的屈服接近度求解函数。但这些新方法尚未应用于基坑工程建设中，无法对施工过程形成有效的指导。

为了对深基坑工程施工过程中周边土体未进入塑性状态的危险区域进行有效划分，采用屈服接近度算法对这些区域的安全性状态进行评价研究。通过与有限差分法计算结果的对比分析，证明这种方法的准确性与适用性。基于屈服接近度概念对基坑整体开挖过程的危险区分布与变化过程进行计算，计算结果可为基坑施工过程中的安全性评价提供参考。

1 基坑安全性的屈服接近度模型

屈服接近度(yield approach index，简称YAI)[10-12]可广义地表述为： 描述一点的现时状态与相对最安全状态的参量的比，YAI∈[0,1]。相对于某一强度理论则可以定义为： 空间应力状态下一点沿最不利应力路径到屈服面的距离与相应的最稳定参考点在相同罗德角方向上沿最不利应力路径到屈服面的距离之比。假设案例中岩土为理想弹塑性体，强度准则为摩尔-库仑准则[13-14]：

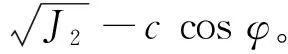
(1)

式中：I1为第一主应力不变量；J2为第二偏应力不变量；φ为内摩擦角；θσ为应力罗德角。

式(1)在π平面上可表示为

(2)

令

D=-ccosφ。

式(2)可整理为

F(σπ,τπ,θσ)=Aσπ+B(θσ)·τπ+D。

(4)

子午面上一点的应力状态见图1。 由三角关系：

则屈服接近度定义为

点C坐标满足式(4)，则

(7)

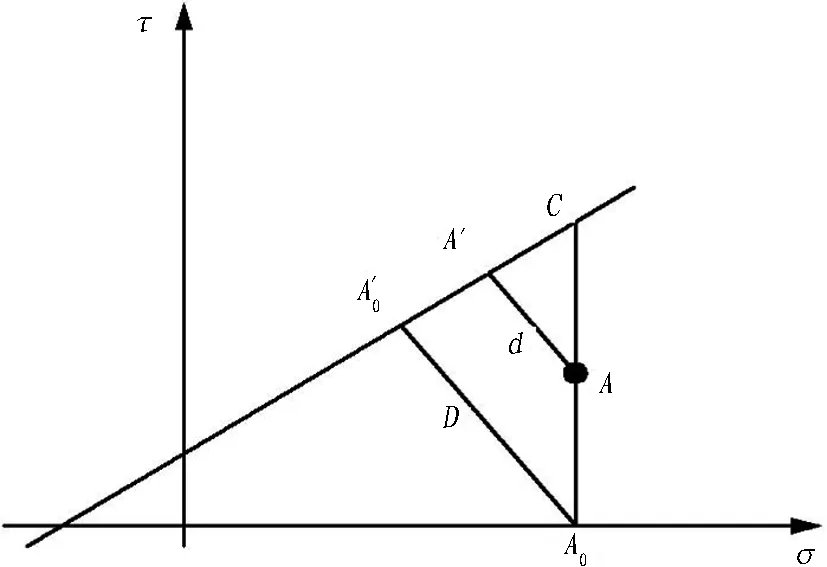
图1 子午面上一点的应力状态

式(7)带入式(6)可得

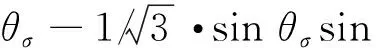
(8)

式(8)即为摩尔-库仑准则下的屈服接近度表达式。

为了便于表达，令f′(σπ,τπ,θσ)=1-f(σπ,τπ,θσ)，即在本文中，屈服接近度接近于1意味着趋于稳定，反之则趋于破坏。

相较于传统的计算方法，屈服接近度的表达实现了非塑性区域安全程度与所处状态的评判计算，将传统意义上的“安全区”进行了详细划分，并给出每个区域的屈服接近程度，以便于及时发现与处理潜在的安全隐患，为工程安全提供保障。

2 工程背景与计算模型

2.1 工程背景

井冈山路站是青岛市红岛—胶南城际(井冈山路—大珠山段)轨道交通工程(简称R3线)和青岛地铁1号线的T型换乘站，位于长江中路与井冈山路交叉口。R3线车站位于井冈山路下方， 1号线车站位于长江中路下方，均为地下岛式双线车站。长江中路现状道路宽度约37 m，双向8车道，道路红线宽70 m，车流量较大。1号线井冈山路站场区东南侧为利群集团超市，东北侧为佳世客超市，西南侧为集力集团基坑(现状坑深约13 m)、家佳源超市，西北侧为世纪商城，建筑环境较为复杂。车站主体基坑东侧有1座南北走向的地下暗渠，埋深约1.2 m，暗渠宽15 m,高1.8 m，暗渠边缘距离1号线井冈山站东侧围护结构边缘为0.2～0.5 m。

井冈山路站1号线车站场区为剥蚀斜坡，地势较为平坦。第四系土层主要为全新统人工填土、淤泥质粉质黏土，下伏基岩为白垩系凝灰岩。其中杂填土及淤泥质粉质黏土层工程性质较差。下伏强风化凝灰岩、中风化凝灰岩，力学性质较好，均匀性也较好，可作为良好的地基持力层。

钻孔勘察结果表明： 场区岩体受强烈挤压作用脆性破裂成碎块和砂土状，原岩为花岗斑岩，矿物蚀变现象明显，局部夹有数cm至十几cm宽的泥状破碎物，形成风化深槽。根据钻孔揭示： 本段基岩为中生代燕山晚期侵入岩，主要为花岗斑岩，局部夹有煌斑岩岩脉。节理裂隙受区域性断裂构造控制，通过钻孔岩芯揭示，节理结构面一般较平直，紧闭—闭合，少量微张并有充填物，多为高角度节理，倾角一般为60°～85°。上述破碎带(断裂、断层、节理、裂隙)对地铁工程的影响主要表现为岩体节理裂隙发育，岩体破碎，形成相对不均匀的岩石地基和安全性较差的岩土体。

复杂的建筑环境及地质条件，须在施工设计过程中充分考虑基坑开挖施工可能引起的地面沉降及周边建筑物倾斜等问题，故对塑性区及危险区域的合理划分显得尤为重要。

2.2 计算模型

基于现场情况，基坑模型计算尺寸设置为10 m×62 m×9.3 m，三维模型长度(Y方向)为165 m，宽度(X方向)为100 m，高度(Z方向)为50 m。其中，围护桩采用FLAC3D软件中pile结构单元模拟，地下连续墙采用liner单元。X、Y方向均为水平约束边界，底部为水平垂直三向约束边界，地表为自由边界，计算模型共38 726个节点、48 957个单元，岩土体的本构关系采用Mohr-Coulomb屈服准则。基坑开挖模型如图2所示。基坑支护模型如图3所示。

图2 基坑三维模型

图3 基坑支护结构模型(1/2模型)

根据地质勘测资料，模型最上层为4 m厚的素填土，中层为2 m厚的红黏土，下层为凝灰岩。初始应力设为自重应力。各地层参数如表1所示。

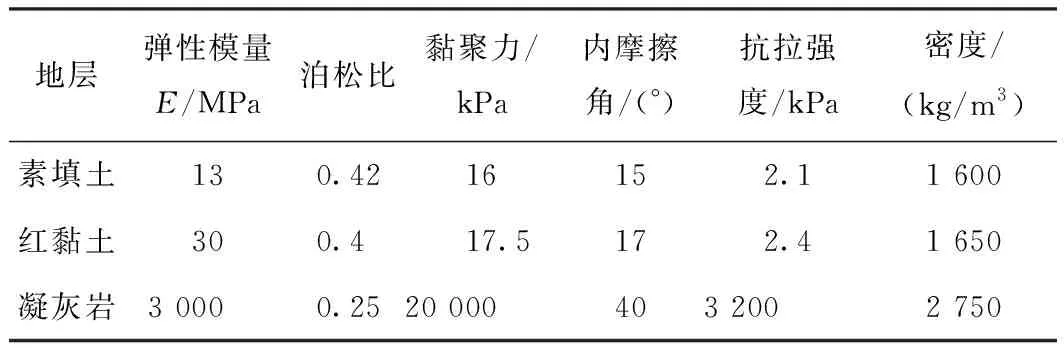
表1 各地层参数

基坑开挖步骤遵循现场施工方法，采用分布开挖、预留两侧土体的形式，共分为4层，开挖高度分别为2、2、3、2.3 m，即总共分8步开挖。在基坑模拟开挖第2步后施加第1道钢支撑，钢支撑距离地表0.5 m。模拟开挖第5步后施加第2道钢支撑，第2道钢支撑距离第1道钢支撑4 m。基坑开挖工法示意如图4所示。

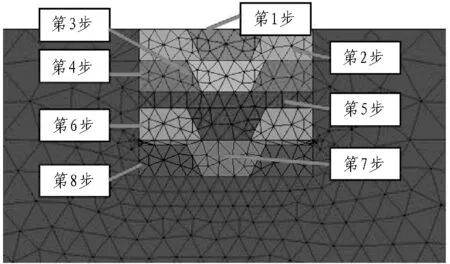
图4 基坑开挖方法示意图

3 计算结果分析

通过fish语言编制描述计算屈服接近度YAI的程序，针对前文中建立的模型利用有限差分算法进行计算求解，并在其所求得的应力结果基础上，结合弹性屈服准则进行进一步的YAI分布求解，从而判断未进入塑性区岩土体的安全程度分布状态。

3.1 2种计算方法对比分析

基坑开挖后危险区分布如图5所示。可以看出： 1)基坑开挖后，塑性区集中于坑壁偏上侧与坑边附近，屈服接近度的值在这些位置的屈服接近度接近于1，并向四周逐渐缩减； 2)基坑底部无塑性区分布，屈服接近度接近于0。

基坑模型Y方向中部X-Z剖面周边土体屈服接近度分布与竖向位移变形云图如图6所示。可以看出： 1)竖向变形集中于基坑上部两侧浅层地表，屈服接近度趋于1，说明该区域存在危险性； 2)基坑底部存在部分隆起变形，但是屈服接近度趋于0，说明该位置处安全性较好。

(a) 塑性区分布

(b) 屈服接近度分布

Fig. 5 Distribution of dangerous zone after foundation pit excavation

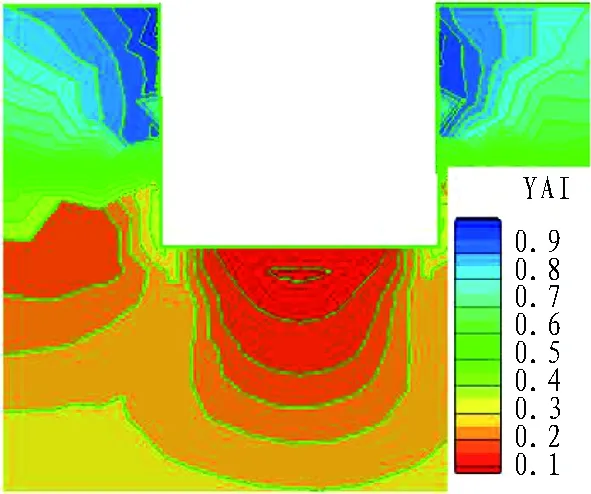
(a) 屈服接近度分布

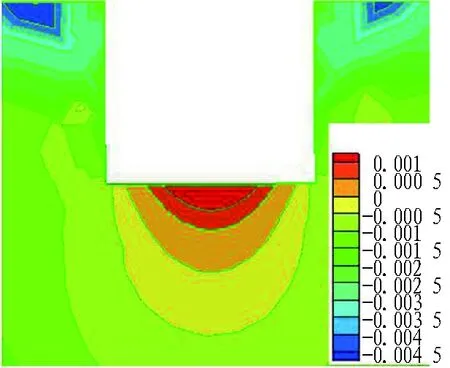
(b) 竖向变形云图 (单位： m)

Fig. 6 Nephograms of YAI distribution and deformation of surrounding soil of foundation pit

基坑模型Z方向中部位置X-Y剖面周围地表屈服接近度与竖向变形分布如图7所示。可以看出： 1)基坑侧壁最大变形量约4.8 mm，最大屈服接近度约为0.85； 2)竖向变形量沿基坑开挖位置向外侧逐渐减小，屈服接近度逐渐趋于0。

(a) 地表屈服接近度分布

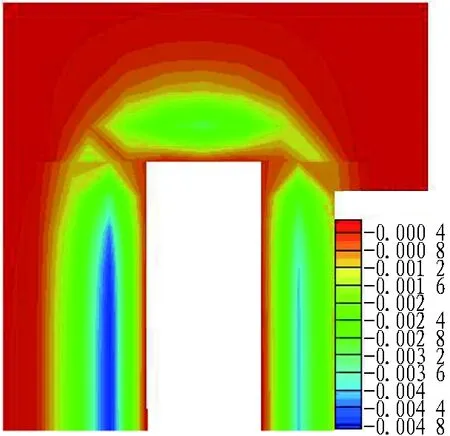
(b) 地表竖向变形云图 (单位： m)

Fig. 7 Nephograms of YAI distribution and deformation of ground surface around foundation pit

图5—7结果表明： 1)屈服接近度算法可较准确地描述塑性区域的分布情况，在此基础上，同时可以描述未进入塑性状态单元体的屈服程度，对仍处于弹性阶段的区域进行安全程度划分，为基坑施工过程中的安全评价提供参考； 2)施工开挖位置附近屈服接近度逐渐增大，相应位置处竖向变形量也随之呈上升趋势； 3)屈服接近度较大位置对应较大的位移变形，通过对基坑开挖过程的屈服接近度分析可提前确定施工危险位置，在施工过程中加强对这些位置的变形监测以及加固处理，从而保证工程安全有序进行。

3.2 基坑开挖过程的屈服接近度分析

为了进一步描述基坑开挖过程中屈服接近度分布形势的变化规律，通过YAI计算程序对基坑开挖过程进行计算，计算结果如图8所示。可以看出： 1)基坑开挖初期，整体屈服接近度约为0.35，坑边有小范围区域达到了0.45； 2)开挖至第4步时，屈服接近度大于0.45的区域显著增加； 3)最小屈服接近度约为0.9，这个区域随着开挖的进行不断增大，第6步开挖后中心部位屈服接近度趋于1，说明该位置已屈服，进入塑性状态； 4)第6步到第8步开挖过程中，屈服接近度分布态势变化不明显，说明初期开挖与支护完成后，基坑整体趋于稳定。

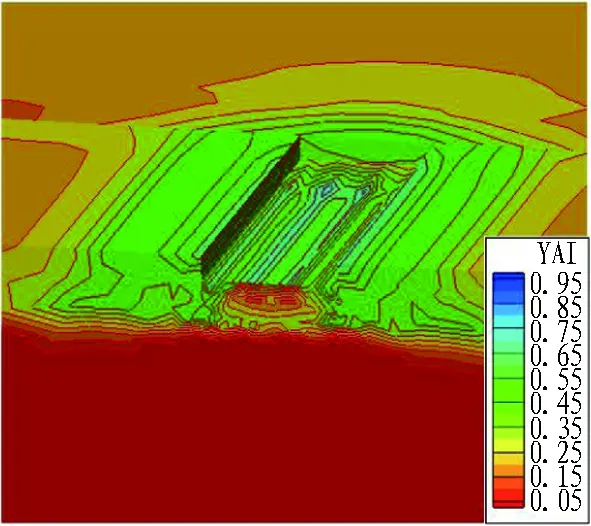
(a) 第2步开挖

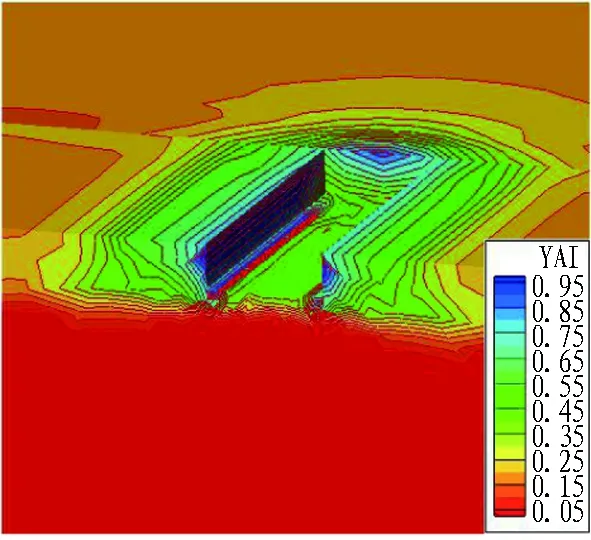
(b) 第4步开挖

(c) 第6步开挖

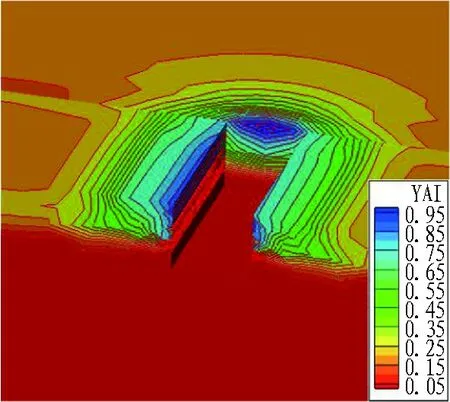
(d) 第8步开挖

Fig. 8 Nephograms of YAI distribution during foundation pit excavation

为了更加直观、详细地统计分析基坑开挖过程中周边土体与地表位置屈服接近度的变化趋势，在基坑一侧选取若干单元作为监测点进行计算统计。屈服接近度监测点布置方式如图9所示。基坑周边土体屈服接近度分布曲线如图10所示。基坑周围地表屈服接近度分布曲线如图11所示。

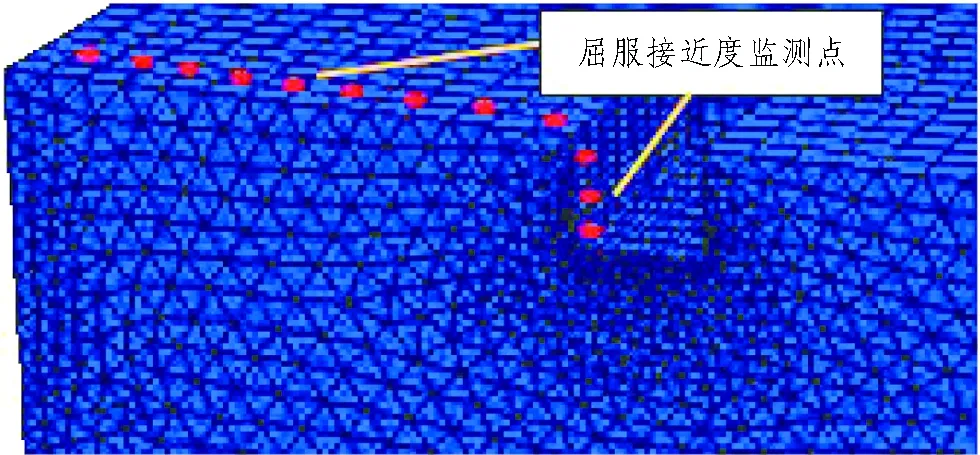
图9 屈服接近度监测点布置方式示意图

图10 基坑周边土体屈服接近度分布曲线图

Fig. 10 Curves of YAI distribution of surrounding soil of foundation pit

由图10可知： 1)第4步开挖后，侧面土体的屈服接近度由约0.5跃迁至约0.9，说明在此过程中基坑安全性存在大幅调整，须加强监测与支护； 2)第6步开挖后屈服接近度分布曲线几乎重合，说明基坑周边土体在此后的开挖过程中处于稳定状态。

由图11可知： 大屈服极限度范围集中于基坑周边20 m内，其中0～10 m屈服接近度值的变化幅度较大，应重点监测控制。

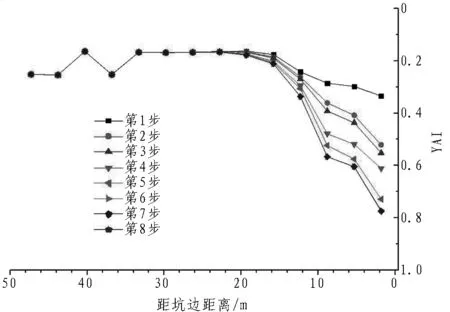
图11 基坑周围地表屈服接近度分布曲线

Fig. 11 Curves of YAI distribution of ground surface around foundation pit

4 结论与讨论

本文在分析基坑工程施工阶段力学性能的基础上，引入屈服接近度概念对工程区域进行区域安全度评价，实现了施工过程中工区周边土体未进入塑性状态危险区域的有效划分，并在此基础上将计算结果与有限差分法计算结果进行对比分析，得出如下结论。

1)屈服接近度算法可有效实现对基坑工程未进入塑性区岩土体危险程度的划分，为施工风险防范提供数值计算基础。

2)通过与有限差分法计算结果的对比发现，屈服接近度分布可实现对塑性区分布状态的有效表达，说明了这种方法的适用性与可靠性。

3)屈服接近度算法可有效应用于基坑开挖的整体过程中，为这个过程下的基坑安全性评价提供可靠参考。计算结果实现了非塑性区岩土体等级划分，但是每个等级所对应的具体安全性评估指标与相应的加固措施仍需进一步研究完善。

本文实现了基坑工程非塑性区的安全性评价，在此基础上对已处于塑性区的岩土体的进一步详细划分还有待研究，因为塑性并不意味着破坏，塑性区破坏程度的定义对基坑安全防护的具体实施具有指导性作用。与此同时，在岩土体进入塑性区后，其塑性程度及其所对应的危险程度、预计变形量的计算还有待下一步进行研究，考虑屈服接近度与塑性程度间的本构关系，从而形成基坑岩土体破坏全过程的安全性评价体系。