高温高盐油藏化学驱数值模拟技术进展

胡 渤

(中国石化 油田勘探开发事业部，北京 100728)

化学驱是大幅度提高油田采收率的重要技术手段，而高温高盐油藏是我国化学驱技术当前的主要应用阵地。目前，国内东部老油田聚合物驱覆盖储量15×108t，面对高温高盐的苛刻油藏条件，常规的化学驱技术适应性不足，研发应用更高效的化学驱油体系进一步提高高温高盐油藏采收率，不断拓展化学驱技术应用新阵地，对老油田持续有效发展具有重要意义。

近年来，针对高温高盐油藏，国内提出了非均相复合驱油体系、增粘型乳液表面活性剂等新型化学驱油体系并取得了显著的矿场应用效果[1-3]。非均相复合驱体系包含三种化学驱油剂：聚合物、表面活性剂以及带有分支的粘弹性颗粒胶体。粘弹性颗粒在水中呈现为分散状的固体，与水相存在明显的界面，因此称为非均相，其主要分子设计思路是通过多点引发将丙烯酰胺、交联剂、支撑剂等聚合在一起，形成交联网络结构，因而具有较好的弹性和耐温抗盐性能，颗粒溶于水后吸水溶胀，能够变形通过孔喉，可以有效解决强非均质油藏中驱油剂窜流问题。乳液表面活性剂是一种新型耐高温驱油剂，在中、低渗透油藏中相比聚合物易于注入，在一定的油水比条件下，与油水作用形成高粘度油包水型乳状液，扩大波及体积，从而提高油藏采收率[4]。

关于粘弹性驱油剂及乳液的流变性、机理研究，研究人员发表过相应的成果[5-10]。但其数学模型难以描述非均相体系的非连续运移特征或乳液体系乳化增粘的机理，亦或引入了大量难以通过实验获取的复杂微观参数。与水驱相比，化学驱的机理更复杂，数学模型不仅要考虑油、气、水各相的方程，还需对各种化学剂组分方程进行计算，对计算效率的要求更高[11-13]。本文在实验分析的基础上，建立了反映两类新型驱油体系驱油机理的数学模型，开发了相应的软件功能，改进了数学模型快速求解算法，实现了新型化学驱数值模拟方法的规模化矿场应用。

1 化学驱油新体系机理研究与数值模拟功能实现

1.1 非均相复合驱数值模拟方法

1.1.1 粘弹性驱油剂主要物化性能与渗流特征

研究证明，粘弹性驱油剂溶液表观粘度随浓度增加而逐渐增大，当矿化度增加时，粘弹性驱油剂溶液表观粘度逐渐减小。与聚合物驱的实验研究结果不同，当粘弹性驱油剂注入后，其残余阻力系数与渗透率呈反比关系变化，因此该体系具有封堵高渗层、提高低渗层动用的特征和作用[14]。由于粘弹性驱油剂分子结构中存在大量交联网状结构，因而其在多孔介质运移过程中能够呈现暂堵、运移、变形通过等多种运动方式，实现对驱替流体的动态转向，进一步扩大波及体积。

1.1.2 非均相复合驱数学模型

关于聚合物和表面活性剂的数学模型，文献中的描述较为成熟[11-13]，在此不再赘述。本研究中仅考虑粘弹性颗粒驱油剂的质量守恒方程和物理化学参数模型。

1) 粘弹性颗粒驱油剂数学模型假设条件

① 地下流体仅考虑油、水两相，并且相间不存在质量交换。

② 聚合物、表面活性剂在水相中呈连续的溶液形式，为均相物系。

③ 粘弹性颗粒在地面溶胀，也考虑为水相中的一种组分，但是与水运移不同步。

2) 粘弹性颗粒运移过程描述与质量守恒方程

当粘弹性颗粒通过孔喉的时候，在小孔喉处会封堵、沉积，在大孔喉中继续运移，随着在大孔喉中进入的颗粒增加，其封堵作用逐渐增强，促使液流向小孔喉转向。同时，随着颗粒在孔喉中逐渐堆积，孔喉两端的压差越来越大，增大到一定程度，迫使具有较好粘弹性的颗粒发生拉伸形变并通过孔喉。因此，从颗粒的运移过程来看，为反映其流动规律，需要重点体现其沉积滞留带来的堵塞效应、变形通过和运移带来的粘弹性驱油效应，为此，建立如下的粘弹性颗粒质量守恒方程：

(1)

式中：Φ表示岩石孔隙度，%；Sw表示水饱和度，%；CPPG表示粘弹性颗粒的质量浓度，%；β是粘弹性颗粒的孔喉通过系数，无量纲；vw表示水流速度，m/d；QPPG为源汇项，m3/d。

公式(1)中，为描述粘弹性颗粒在多孔介质中的堵塞与重启动，以及颗粒与水运移的不完全同步性，定义了一个新的参数：孔喉通过系数。孔喉通过系数表示孔喉中随水流动的颗粒质量浓度与水中颗粒总质量浓度的比值，是颗粒在通过孔喉过程中微观流动特征的宏观表现，室内实验研究表明，其取值与孔喉处的压差、颗粒注入的浓度、颗粒的粒径有关。

粘弹性颗粒在孔喉中封堵与变形通过的过程，宏观上表现为颗粒运移存在一定的启动压力，而这个启动压力仅为颗粒本身的属性，而不是指水相存在启动压力。因此，在孔喉通过系数中将颗粒的启动压力也反映进去：

(2)

式中：pmax即为粘弹性颗粒的启动压力，MPa。由公式(1)和(2)可知，压力小于启动压力时，孔喉通过系数为0，质量守恒方程的对流项为0，孔喉中只有颗粒流入、沉积，当压力逐渐增大至超过启动压力后，孔喉通过系数大于0，公式(1)中的对流项开始起作用，颗粒开始运移。从以上的描述来看，孔喉通过系数能够反映粘弹性颗粒封堵、变形通过、运移的过程。

3) 粘弹性颗粒物理化学参数模型

① 封堵模型

与聚合物相似，粘弹性颗粒的封堵的作用主要体现在降低水相的渗透率，因而可以通过残余阻力系数来进行数学表征。室内实验研究表明，残余阻力系数和粘弹性颗粒的浓度、岩石渗透率、流体的流动速度有关，其影响规律与传统的聚合物、凝胶等驱油剂不同。基于实验数据，回归得到了如下的残余阻力系数(RPPG,μm2)函数关系式：

(3)

式中:Rkmax为无量纲参数，取值与岩石孔隙度、流体中的离子浓度有关；K为岩石渗透率，10-3μm2；α1，α2，b为无量纲参数，可通过实验数据拟合得到。

② 增粘模型

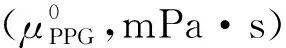
(4)

粘弹性颗粒本身的分子设计中存在部分聚合物基团，因此，在多孔介质中运移也存在剪切效应，考虑剪切的粘度(μPPG,mPa·s)公式为：

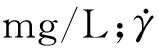
1.1.3 室内实验拟合

利用本研究形成的数值模拟方法对室内实验结果进行拟合，实验模型为非均质的两个填砂管，高渗管渗透率3 000×10-3μm2，低渗管渗透率1 000×10-3μm2，填砂管中仅饱和水，为单相模拟实验。注入段塞设置为：水驱至注入1.43倍孔隙体积，转为聚合物驱，聚合物溶液注入浓度为2 600 mg/L，至2.75倍的孔隙体积后再转为水驱，直至高渗管分流量达到95%以上，开始注入聚合物和粘弹性颗粒的复合体系，注入浓度均为1 200 mg/L，到注入6.5倍孔隙体积后，改为后续水驱。

图1中的产液百分数即为单管的产液量占总产液量的百分比。根据图1的拟合结果，证实了本文建立的模拟方法能够有效反映粘弹性颗粒液流转向的主要机理。

1.2 增粘型乳液表面活性剂驱数值模拟方法

1.2.1 增粘型乳液表面活性剂驱油机理及数学描述方法

增粘型乳液表面活性剂的数学模型基本假设与传统的低张力表面活性剂类似[11-13]，表面活性剂作为水相中的一种组分，其质量守恒方程为：

(6)

图1 非均质双管实验分流量拟合Fig.1 Fitting of the heterogeneous dual tubes flow experiment

1) 增粘型乳液表面活性剂粘度模型

室内实验研究表明，增粘型乳液表面活性剂的主要驱油机理是在一定的活性剂浓度和油水比条件下形成油包水型的乳状液，增加驱替相的粘度，改变油水流度比，提高波及体积。乳状液的粘度变化主要受表面活性剂浓度和含水饱和度两个指标控制，表面活性剂浓度决定是否乳化，含水饱和度决定乳化后的粘度。根据实验测试，乳液表面活性剂粘度与含水饱和度的关系如下。

在实际应用中，乳液粘度计算模型可以直接采用实验曲线插值得到，关系式为：

m=f(Sw,Cew)

(7)

式中：m为乳液表面活性剂的粘度，mPa·s；Sw为含水饱和度，%；Cew为乳液表面活性剂在水相中的浓度，mg/L。

2) 乳液表面活性剂封堵模型

实验研究表明，乳状液在岩心中渗流时压力梯度较高，压力波动大，说明乳液颗粒在其中运移时存在滞留现象，其中部分滞留的乳液颗粒对岩心孔道产生封堵效果，使液流转向，从而提高乳液以及后续水驱的波及体积。乳液表面活性剂的封堵作用主要通过残余阻力系数来描述，残余阻力系数受乳液与孔喉的匹配性影响较大，实验结果如表2。

其中，残余阻力系数为封堵前后岩心渗透率的比值，用于表征乳液对岩心封堵性能的强弱。从表2可以看出，随着粒径的增大，乳液的残余阻力系数逐渐增加，如果仅从封堵调剖的效果上评价，当乳液粒径大于岩心平均半径时，残余阻力系数最大，乳液达到最强的封堵效果。

此外，通过室内实验研究，分析了乳液表面活性剂浓度对残余阻力系数的影响，结果如表3。

从表中可以看出，虽然乳液的浓度不同，但是3组实验的结果相近，残余阻力系数都是90左右。综合表2和表3的结果及认识，得到乳液表面活性剂注入后残余阻力系数的函数(RK)关系式为

RK=f(φe,K)=a1K2+a2K+a3

(8)

式中：a1,a2,a3为通过实验数据拟合得到的系数，与乳状液粒径中值相关，无量纲；φe为乳状液的粒径中值，μm。

3) 乳液表面活性剂吸附模型

室内实验研究认为，乳液表面活性剂在岩心中存在吸附现象，吸附量受表面活性剂浓度、含盐度等因素的影响，吸附规律与传统的低张力表面活性剂类似，因此，在吸附数学模型中仍可以采用国际上通用的Langmuir公式[11]，在此不再赘述。

表1 乳液表面活性剂粘度与含水饱和度的关系(110 ℃)Table 1 Relationship between emulsification and viscosification of emulsion surfactant and water saturation(110 ℃)

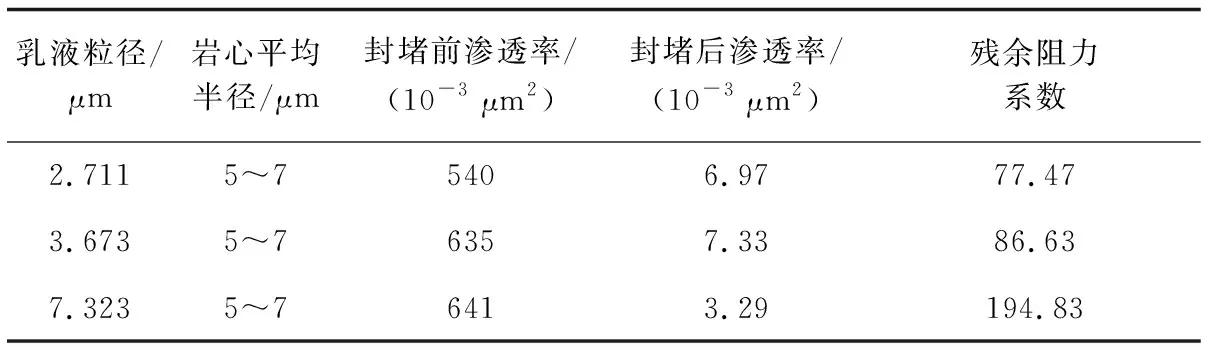
表2 岩心参数及实验结果Table 2 Core parameters and experimental results

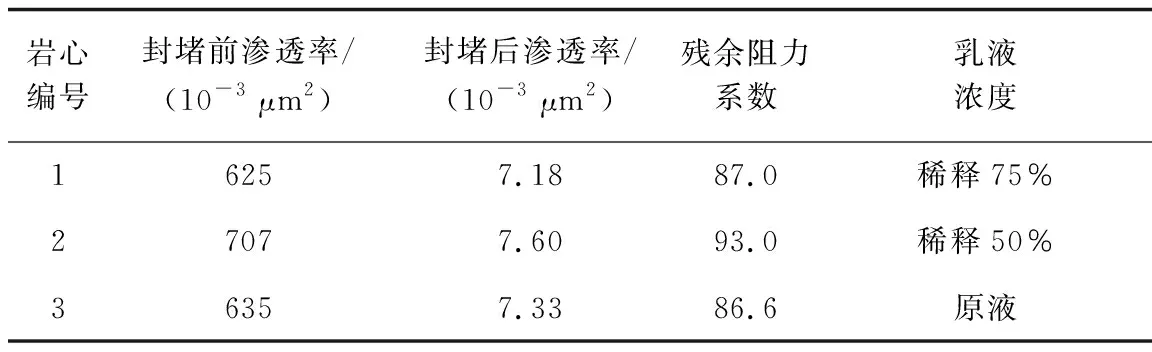
表3 岩心参数及实验结果Table 3 Core parameters and experimental results

1.2.2 室内试验结果拟合

采用三层非均值模型进行室内实验模拟，模型孔隙度为15.0%，初始含油饱和度为0.57，模型3个层的渗透率分别为2 000×10-3,4 000×10-3,8 000×10-3μm2。实验所用模拟油密度为0.9 g/mL，粘度为35.2 mPa·s，实验温度为60 ℃，乳液表面活性剂质量浓度为0.3%。

注入段塞设计为：以2.9 m/d的速度注入1.5～1.8倍孔隙体积的地层水，当产出液含水率大于98%时，注入0.3倍孔隙体积的乳液表面活性剂段塞，然后继续注入地层水直至产出液含水率大于98%时结束。

图2是该实验的采出液含水率和模型采收率的拟合结果，计算结果与实验测试数据吻合度较高，证明数学模型能够有效反映乳液表面活性剂的驱油特征。

图2 乳液表面活性剂驱含水率与采收率拟合结果Fig.2 Water-cut and recovery fitting results of emulsion surfactant flooding

2 化学驱数值模拟快速求解算法

2.1 计算方法

目前，化学驱数值模拟的主要数学模型仍以压力方程、组分浓度方程和饱和度方程这样的解耦形式模型为主[11-13]，针对此种形式的数学模型，胜利油田开展了针对压力方程的预处理共轭梯度解法、针对组分浓度方程的上游排序解法、针对整体模型的OPENMP并行解法3方面的改进，取得了良好的计算效率提升效果[15-16]。本文在此基础上，针对压力方程，进一步开展了基于交替方向离散的求解算法改进。以水相压力方程为例，其离散后形成的线性代数方程组简记为：

(9)

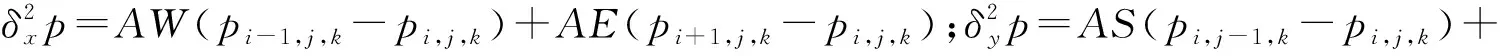
AW，AE，AS，AN,AB，AT，AC为压力方程离散后形成的七对角线性代数方程组的系数；p为水相压力，MPa；i，j，k分别代表x，y，z三个方向的网格编号。对上面的离散方程，分别从x，y，z三个方向构建新型交替方向离散格式：

(10)

(11)

(12)

式中：σ，τ是迭代参数；n为迭代步，无量纲。

2.2 计算效率测试

建立如下的概念模型：网格规模100×104节点(200×200×25)，模拟历史5a，井数116口(水井66口，油井50口)，五点井网，化学剂段塞设置为：300～700 d共注入0.3 PV的聚合物和乳液表面活性剂段塞，其余时间水驱，模型垂向渗透率级差为：1 ∶2 ∶3 ∶4 ∶5(μm2)。压力方程计算方法修改前后，计算时间如下表4所示。

从上表结果来看，在保证计算结果一致的情况下，利用交替方向解法能够增大计算时间步长，大幅度降低整体计算时间(由21.2 h降至2.9 h)，在复合驱模拟上节省85%以上的计算时间。

3 非均相复合驱体系矿场模拟跟踪应用实例

模型选区胜利油田某聚合物驱后先导试验区，试验区采出程度已达到52.3%，综合含水率为98%，在此基础上开展非均相复合驱矿场试验。地质模型的网格规模约48×104节点，平面网格步长10 m。注入段塞设计：639～2 249 d,注入非均相体系主段塞,其余时间水驱。不同软件与方法对非均相复合驱阶段的综合含水拟合结果如图3。

图3的结果说明本文建立的方法能够有效跟踪非均相复合驱矿场动态，通过与商业化软件二元复合驱模拟结果等到对比也进一步说明了这一点。文献[14]对矿场的见效因素与开发机理进行了详细的分析，进一步深化了该方法的矿场应用。

表4 不同计算方法计算速度对比Table 4 Comparison of running time with different algorithms

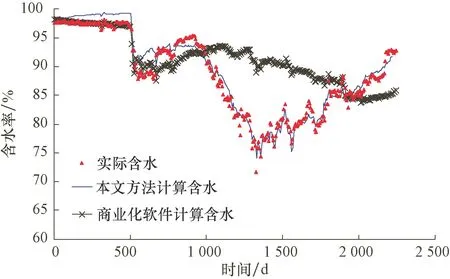
图3 不同数值模拟方法计算含水对比Fig.3 Comparison of water-cut curves obtained from different numerical simulations

4 结论

1) 在室内实验研究的基础上，认识了非均相体系、乳液表面活性剂体系等面向高温高盐油藏开发的新型驱油体系的驱油机理，建立了基于粘弹性颗粒孔喉通过系数的非均相复合驱数学模型以及表征乳液表面活性剂乳化增粘特征的数学模型。

2) 基于自主知识产权的化学驱数值模拟软件SLCHEM实现了相应的模拟功能，开展了室内试验的拟合与矿场模型的应用，验证了数学模型与模拟功能的合理性和准确性。

3) 研发了复杂化学驱体系数学模型快速求解算法，大幅度地提升了SLCHEM软件的运算速度，在网格规模100×104节点、模拟历史5a、井数116口条件下，复合驱计算时间2.9h，实现了百万规模节点的快速运算。

4) 在胜利油田实际矿场区块开展了新体系化学驱数值模拟技术应用，为新型驱油体系的矿场应用建立了历史拟合、动态跟踪、预测调整的技术手段，与商业化软件相比，改进后的SLCHEM软件模拟结果准确反映矿场实际，实现了有效支持生产。