利用光杠杆测量流体压强及流速的微小变化
王小怀
(韩山师范学院 物理与电子工程学院,广东 潮州 521041)
压强测量是流体力学实验技术中最基本的测量技术. 不仅压强本身是表征流体运动过程的重要参量,而流速、流量等参量的测量,也往往转换为压强测量. 本文将流体压强的微小变化转化为U形管或测压管液面高度的变化. 再利用光杠杆放大原理,将液面高度难以判断的微小位移放大成激光光点明显的位移,从而实现了液体压强的微小变化测量.
1 实验装置
光杠杆测量流体压强及流速的实验装置实物图如图1所示. 使用的器材为:激光源、U型管、量筒、自制光杠杆及浮标、螺旋测微计、针筒、坐标纸、三脚架、温度计、卷尺.

图1 实验装置实物图
2 实验原理
对于重力场中的不可压缩均质流体,伯努利方程为[1]

(1)
式中:v为流体流动速度,g为重力加速度,h为流体处于的高度(从某参考点计),p是流体所受的压强,ρ是流体的密度. 在沿流线运动过程中,能量总和保持不变,即总能量守恒. 伯努利方程揭示流体在重力场中流动时的能量守恒. 由伯努利方程可知,流速大处压力低,流速小处压力高.
按图2设计了流体压强变化测量装置,通过节流阀的调节改变流速,根据伯努利方程,流体流速变化将引起流体压强的变化,从而使测压管内液面高度产生变化. 同样,只要能精确测出测压管内液面高度的微小变化,利用伯努利方程,就可实现液体流速或压强微小变化的精确测量. 为了提高测量的灵敏度,利用光杠杆放大原理,将液面高度难以判断的微小位移放大成激光光点较大的位移. 而且可以根据需要控制光点的投射距离灵活调节装置的测量灵敏度.
为了简化实验装置及操作过程,提高测量稳定性,设计了流体压强微小变化的简化测量方案,如图3所示.
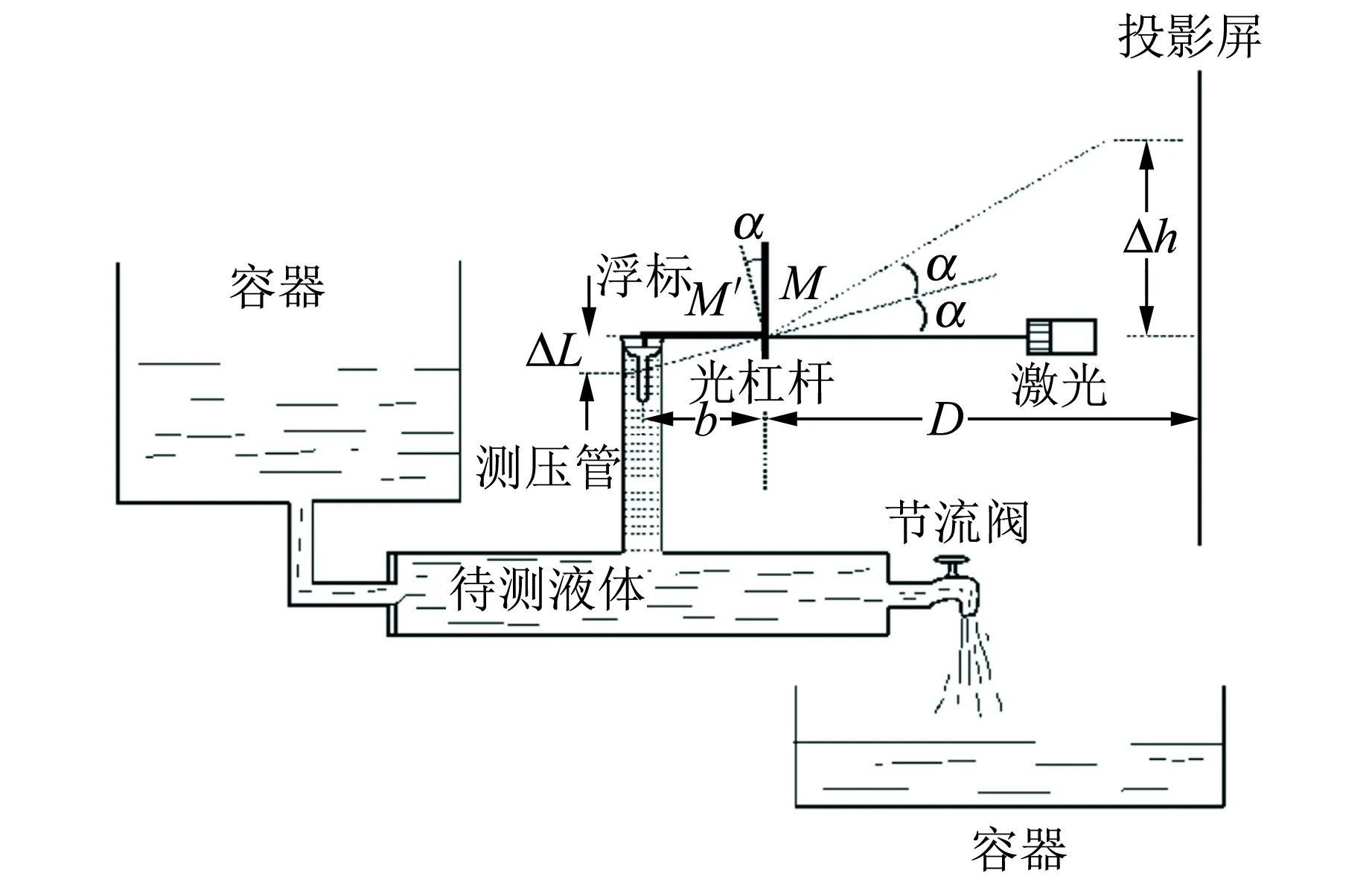
图2 流体压强变化测量示意图

图3 简化实验装置
该装置用量筒替代导流管,U形管取代测压管,利用螺旋测微计测量杆推动注射器实现对微小压强变化的可靠调节.
待测液体压强未发生变化时,浮标的初始位置为Lo. 当液体压强发生变化时,浮标跟随液面上下移动了ΔL,并使光杠杆镜面转动α角. 相应的,经光杠杆镜面反射后的光点在垂直放置的投影屏上移动了Δh距离. 从图3中几何关系可知
(2)
(3)
其中b为光杠杆后足到前足连线的距离,D是投影屏到光杠杆镜面的距离. 当α很小时,tanα≈α,tan (2α)≈2α,于是近似有
(4)
(5)
联立(4)~(5)式,可得
(6)
通过转动旋螺旋测微计旋钮,螺杆带动针筒活塞,使得测量液体内部压强发生了微小变化Δp. 由于液体传递压强的作用,使得U型管中的压强也发生变化,浮标移动ΔL,从而使U形管两侧的液面高度差变化2ΔL,根据p=ρgh可得,待测液体内部压强变化为
(7)
因U型管中水的密度ρ、重力加速度g以及光杠杆后足到前足连线距离b均为定值,故待测液体压强变化Δp与光点移动距离Δh成正比,与投影屏到光杠杆镜面距离D成反比.
3 实验及分析
3.1 实验数据
实验数据如表1所示[3-4]:液体温度T=24.2 ℃,光杠杆镜面到投影屏的距离D=24 540 mm,光杠杆后足到前足连线的距离b=42.9 mm.
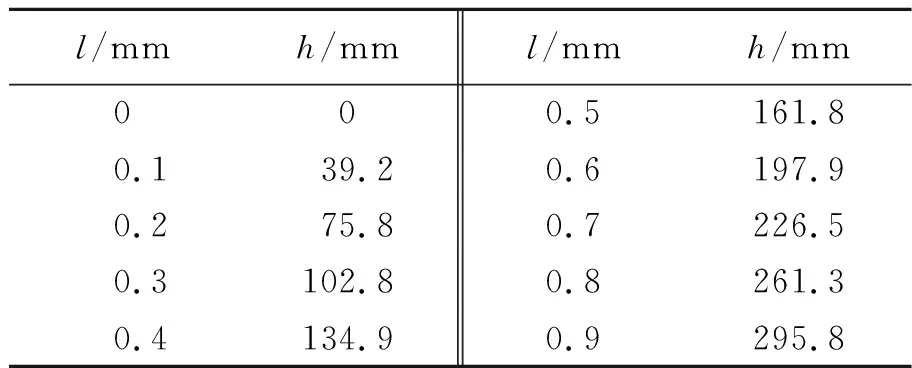
表1 螺旋测微器旋进距离与光点位移数据表
3.2 数据处理及分析
根据表1中数据绘制光点位移与测微计旋进距离关系图,并对其进行最小二乘线性回归处理,拟合结果见图4.

图4 光点位移与测微计旋进距离关系图
可见螺旋测微器的旋进距离l与光点在投影屏上的坐标纸上的移动位置h呈现很好的线性关系,从而反映出待测流体的压强变化与光点的位移之间存在线性关联,与原理分析一致.
采用逐差法计算出螺旋测微器每旋动0.1 mm,光点在投影屏上移动的平均位移Δh为31.62 mm. 并将24.2 ℃时水的密度ρ=0.997 25×103kg/m3和当地重力加速度g=9.788 m/s2将代入(7)式,可求得相应的压强变化Δp=0.55 Pa.
由于微小压强变化引起的待测液体、传递气体及U形管中的水的自身体积变化极小,因此忽略其影响. 于是待测流体内部的压强变化等于U形管中的两液面的压强差,即同为Δp.
4 实验方案后续拓展应用
1)构建真实的流体环境,根据液体流速与压强的关系,通过测量流体压强的微小变化可达到测量流体流速微小变化量的目的. 可实际应用于流体流速的精密监控.
2)根据迈克耳孙干涉仪的干涉原理,让检测液面代替干涉仪的动镜. 利用干涉条纹的移动数N测量出液面的高度变化,从而确定流体的压强差Δp. 理论上,压强差的测量灵敏度可以达到10-3Pa.
3)利用本实验装置,对光点移动与温度微小变化的关系定标,可测量温度的极小变化量,成为灵敏度高的测温装置.
5 结束语
通过导管中的空气将待测液体压强的变化传递并转化为U形管中液面高度变化,再利用光杠杆原理将液面变化有效放大,既提高了测量精度,又避免对待测液体的污染. 螺旋测微计结合注射器实现了对微小压强变化的可靠调节. 浮标采用塑料膨胀管制作,质量轻且不粘壁,能在水中升降自如. 该装置原理清晰,结构简单,操作方便. 实际测试显示其测量灵敏,结果可靠.

