基于模运算的彩色图像隐写算法

肖文国，葛华勇,2，彭阳洋

(1.东华大学信息科学与技术学院，上海 201620； 2.东华大学数字化纺织服装技术教育部工程研究中心，上海 201620)

0 引 言

图像隐写术是一项将信息隐藏在图像后进行隐形传输的技术[1]。最原始的图像隐写术是Petitcolas等人[2]提出的最低比特位(Least Significant Bit， LSB)替换隐写算法。它的原理简单，易于实现[3]，但也容易被直方图和RS(Regular Singular)隐写分析方法发现[4]。LSB匹配[5-6]和动态补偿LSB[7]等隐写算法的提出，能够有效地解决这缺陷。在空域上，除了最常用的LSB算法，还有模运算方法[8-9]。Zhang等人[10]提出的EMD(Exploiting Modification Direction)，是一种利用改变方向的模运算隐写算法，具有良好的载密图像视觉质量和较高的嵌入率。

相对灰度图像而言，彩色图像隐写研究还不够完善。康年锦等人[11]利用视觉感知机理将信息分成2部分隐藏在Y和V分量中，能够提供较大的嵌入率，但安全性一般。马巧梅等人[12]根据RGB通道将彩色图像分解为3幅图像，利用拉格朗日分存算法将信息隐藏在3幅图像中。蔡玮等人[13]根据位平面像素点的亮度来决定嵌入数据的数量，有效地提高了嵌入率，但也增加了时间复杂度。Rabie等人[14]提出根据秘密信息量的大小，在图像的每DCT块中自适应调整像素值的相关量，具有极高的嵌入容量，但是PSNR值一般，且没有任何抵抗攻击的能力。

针对现有的彩色图像隐写术嵌入率低及嵌入率与视觉质量难以协调的问题，本文提出利用模运算性质在彩色图像上的大嵌入隐写算法。该算法可以通过调整密钥的大小，改变算法的嵌入率，而最大嵌入率比现有的大部分彩色隐写算法大，且在嵌入率较大的情况下，图像仍然有良好的视觉质量。

1 基于模运算的嵌入算法

本文提出的基于模运算的嵌入算法流程图如图1所示，主要由6个步骤组成：1)根据选定的密钥n、k确定隐写系数a、b、c；2)将密文转换成2n进制数S(n)；3)根据隐写函数计算出原图像中的原始信息；4)计算密文信息与原始信息的差值d；5)由差值d和隐写函数，计算出修改量ΔR、ΔG、ΔB；6)在原图像中进行修改，即可得到含密图像。

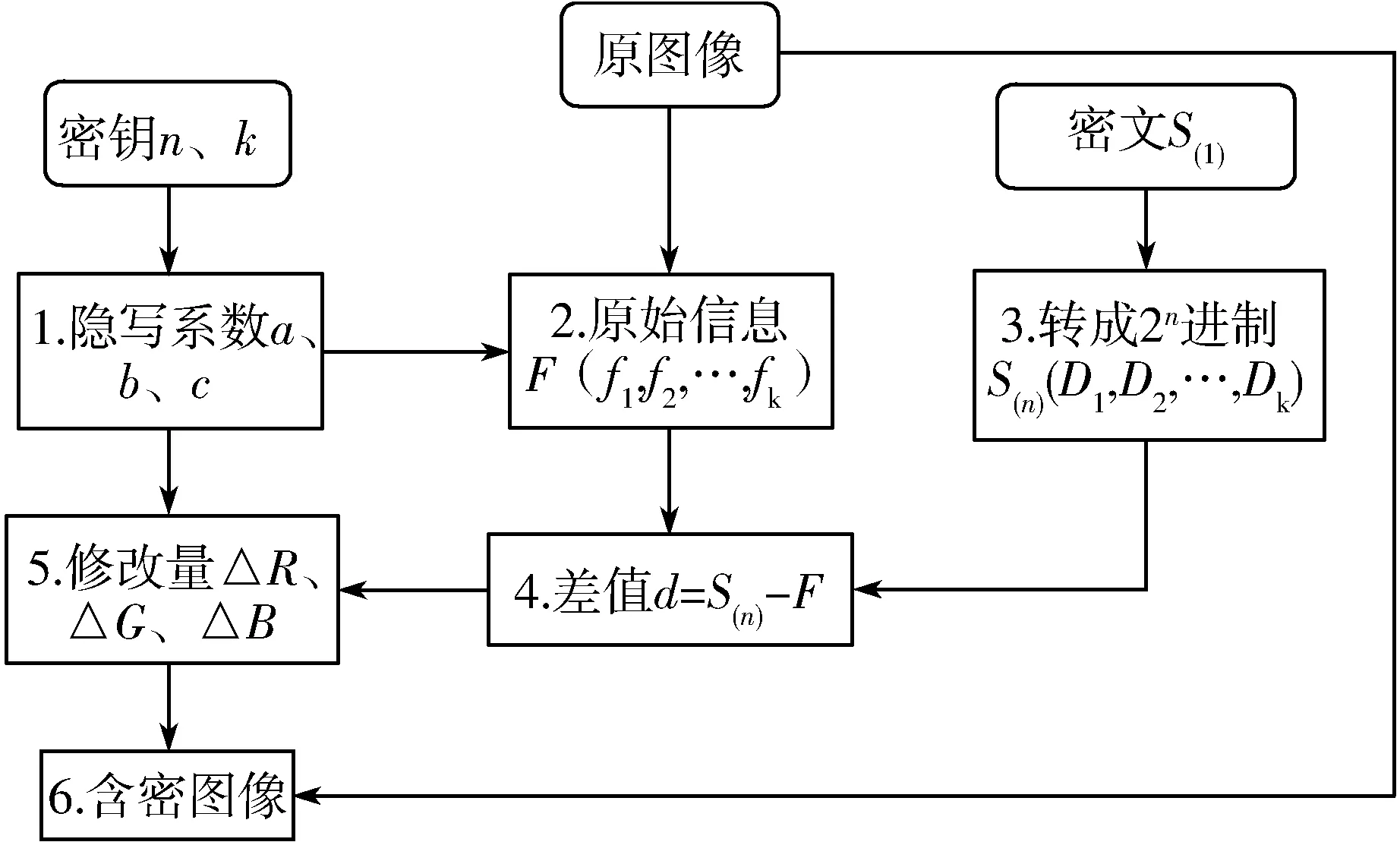
图1 隐写方案流程图

1.1 隐写函数

在介绍隐写函数前，首先了解模运算函数，也就是求余函数，可由式(1)表示：

f=x mod n

(1)

式(1)具有这样的性质：当x的变化量Δx在由式(2)确定的整数集合U中取值时，式(3)成立并且是一对一的映射关系。

U={Δx∈Z|k≤Δx≤k+n,k∈Z}

(2)

{f|f=(x+Δx) mod n}={0,1,2,…,n-1}

(3)

利用该性质，可以通过将像素值x改变为x+Δx来隐藏一位n进制的秘密信息。

彩色图像的每个像素点都由R、G、B这3个信息数据决定，利用R、G、B共同隐藏信息可以提高算法的安全性。对秘密信息隐写的隐写函数可表示为式(4):

D=[a×(G+ΔG)+b×(R+ΔR)+c×(B+ΔB)] mod 2n

(4)

其中，a、b、c称为隐写系数，由密钥n确定，G、R、B分别为原始图像的三维数据，ΔG、ΔR、ΔB分别为三维数据的改变量，D表示秘密信息。与式(3)相类似，在式(4)中可提取出改变量Δx，如式(5)所示：

Δx=a×ΔG+b×ΔR+c×ΔB

(5)

研究表明，人眼对红绿蓝3种颜色的敏感度不同，对绿色(G)最为敏感，蓝色(B)次之，红色(R)最不敏感。为生成视觉质量最佳的图像，应该尽量在最不敏感的数据上修改。经过大量的实验比较，在假设ΔG最大值为A，ΔR最大值为A+1，ΔB最大值为A+2时，可以达到视觉质量的最佳效果。为满足嵌入信息的映射关系，必须使Δx能够遍布1～2n中所有的值，且修改量ΔR、ΔG、ΔB最小。

隐写系数a、b、c的计算过程如下：

1)要满足Δx=1，且考虑到ΔG的最大值最小，因此a=1。

2)当ΔG取最大值时，Δx=A。要满足Δx=A+1，且考虑到ΔR的最大值次之，因此b=A+1。

3)当ΔG、ΔR都取最大值时，Δx=A2+3A+1。要满足Δx=A2+3A+2，因此c=(A+1)(A+2)。

4)当ΔR、ΔG、ΔB都取最大值时，Δx=A3+6A2+11A+5。要满足Δx=2n，因此可由式(6)、式(7)计算A。

i3+6i2+11i+5=2n

(6)

A=「i⎤

(7)

5)最后再由A计算出a、b、c。

本算法提出了一种基于模运算的新型隐写函数，并利用人眼对色彩图像敏感度不同，计算出最佳的隐写系数。

1.2 进制转换

计算机处理的一般是二进制数，对二进制数进行进制转换，一方面可以有效提高安全性，另一方面可以简化数据量，提高嵌入容量。在进制转换前，需要计算另一个参数l，计算过程如式(8)：

l=k×n

(8)

其中，k、n皆为密钥，l表示转换前信息数据的位数，k表示转换后信息数据的位数。首先将秘密信息转化为二进制流S(1)，接着从S(1)中取出l位数据将其转化为k位的2n进制数S(n)，不足k位则补0，用D1,D2,…,Dk分别表示S(n)每一位上的数。

1.3 原始信息及差值

在式(4)中，令ΔG=ΔR=ΔB=0，即可得到未嵌入信息前的图像原始信息，用符号F表示，如式(9)：

Fi=(a×Gi+b×Ri+c×Bi) mod 2n， i=1,2,…,k

(9)

其中，Gi、Ri、Bi表示第i个像素点的三维信息数据。

接着计算2n进制数S(n)与原始信息F间的差值，用d表示，如式(10)：

di=Di-Fi， i=1,2,3,…,k

(10)

差值d可以理解为通过模运算后原始图像与含密图像间的差别，接下来只要根据这个差值计算出原始图像与含密图像的像素值变化量即可。

1.4 修改量

当ΔG最大取值为A，ΔR最大取值为A+1，ΔB最大取值为A+2时，ΔG、ΔR、ΔB可有多种不同的解，取修改量ΔG、ΔR、ΔB的平方和最小的一组解，如式(11)：

(11)

其中，i=1,2,…,k；j=-1,0,1。

最后含密图像的三维数据只需将原图像的数据加上修改量即可，如式(12)：

(12)

其中，i=1,2,…,k。

以(n,k)=(5,4)为例，要隐藏秘密信息00001100101001110101(1)，各像素点数据信息为G1=98，R1=12，B1=25；G2=57，R2=124，B2=51；G3=125，R3=136，B3=10；G4=12，R4=80，B4=65。具体计算过程如图2所示。

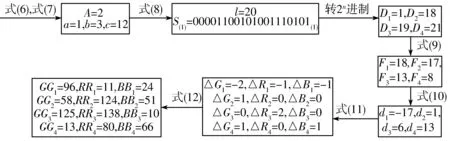
图2 信息嵌入过程

2 信息提取

信息提取隐写算法的另一个重要部分，是信息嵌入的逆过程，需要在含密图像上提取出其中隐藏的信息，如图3所示。

图3 信息提取框图

具体步骤如下：

步骤1给定密钥(n,k)，根据式(6)求得A，计算出隐写系数a、b、c。

步骤2读取含密图像的三维数据，利用式(13)计算秘密信息Di：

Di=(a×GGi+b×RRi+c×BBi) mod 2n， i=1,2,3,…,k

(13)

其中，GGi、RRi、BBi分别是含密图像的三维数据。

步骤3将秘密信息Di表示成2n进制数，以k位为一组转化成二进制，即可得到最原始的秘密信息S(1)。

同样以密钥(n,k)=(5,4)为例，含密图像的4个像素点数据为GG1=96，RR1=11，BB1=24；GG2=58，RR2=124，BB2=51；GG3=125，RR3=138，BB3=10；GG4=13，RR4=80，BB4=66。根据信息提取步骤，可得到图4的信息提取过程。

3 算法优化

3.1 嵌入信息容量

在计算机中，图像也是以二进制数值的形式存储的，不管是原始图像还是含密图像，其本身都会含有大量的信息[15]。在不知道嵌入容量的情况下，提取信息需要遍历整幅图像，可能会得到大量无关的数据，严重降低提取效率，浪费大量的资源，甚至影响信息的准确性。因此在对图像嵌入信息后，有必要指明图像中嵌入信息的容量。

本文采取的方法是在图像中嵌入此次嵌入信息的总容量。具体方法如下：

1)读取图像的分辨率，计算全部像素点的个数g1；

2)将像素点个数g1转换成一个2n进制数g2，计算g2的位数m，保留图像的前m个像素点，用来隐藏此次隐写的容量；

3)在信息隐写完毕后，读取含密像素点的总个数h1，将h1转换成2n进制数h2；

4)将h2以本文隐写算法的方式隐藏在m个像素点中。

实例图像的分辨率为512×512像素，密钥(n,k)=(5,4)，含密像素点个数h1=72832。

首先计算总像素点个数g1=262144，转换成2n进制数g2=8000，g2共4位即m=4，h1转换成2n进制数h2=2740。也就是说，在图像的前4位像素中分别隐藏2、7、4、0。

通过在图像的固定位置嵌入此次的隐写容量，可以在提取信息前就能得知哪些像素点隐藏有信息，对算法的隐写时间有很大的优化，并能有效地避免在提取时信息带来的错误。

3.2 像素边值调整

根据上述假设，ΔG最大值为A，ΔR最大值为A+1，ΔB最大值为A+2。也就是说三维改变量的范围如式(14)：

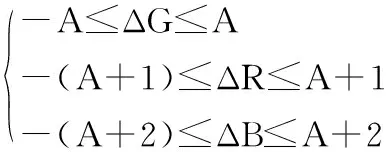
(14)

每个像素点的数据范围都是0～255，当像素值为边值时，即0或255时，此时不能再减去或加上修改量，直接计算差值可能会导致数据溢出的现象，因此需要对边值进行调整。具体修改方案如式(15)～式(17)：

(15)

(16)

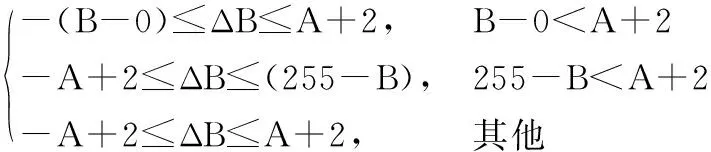
(17)

经过像素边值调整，可以使图像中的所有像素值都能在可操作的范围内运算，并以最小的改变量实现信息隐藏，保证图像良好的视觉质量。

4 实验结果与分析

本文通过大量实验分析验证了该算法的有效性和可行性，在此以512×512的airplane、baboon、lena、peppers等4幅彩色图像为例说明实验结果。本实验在系统为Windows 8的电脑上进行，仿真工具是Matlab2013a。

衡量隐写算法的性能指标主要有2方面：一方面是嵌入容量，另一方面就是安全性。

4.1 嵌入容量

本文隐写算法的嵌入容量主要是由密钥n决定的。由于彩色图像存在RGB三维数据，因此彩色图像的一个像素点均表示3位数据位[16]，其嵌入率可由式(18)计算得出：

(18)

嵌入容量可由式(19)表示，其中，y、z分别表示图像的宽度、高度。

Q=⎣⎣(y×z-⎣log10(y×z)」-1)÷k」×n×k÷16」×16

(19)

以本次实验的512×512图像为例，具体的嵌入率及嵌入容量如表1所示。

表1 不同n对应的嵌入容量

由表1可见，在彩色图像中嵌入容量约为百万数量级的，可安全隐写大量的数据。

4.2 安全性

安全性可分为2个部分讨论：图像视觉质量和抗分析能力。

4.2.1 图像视觉质量

图像视觉质量通俗地说，就是含密图像与原图像相比较，是否能够达到无法区分的效果。本算法在不同的嵌入率下测试，均能达到理想效果。图5是嵌入率为4 bpp时的含密图像，在这样大嵌入率的情况下，图像也没有出现丝毫的失真。

airplane

baboon

lena

peppers

峰值信噪比(PSNR)是一种评价图像的客观标准，它的单位为dB。PSNR值越大，就代表失真越少。一般而言，当2幅图的PSNR大于35 dB时，人眼看不出区别；当PSNR大于38 dB时，达到理想的图像视觉质量要求。在密钥n取3～10之间，由本隐写算法生成100幅含密图像，分别计算其均方差与PSNR，求得平均值如图6和图7所示。

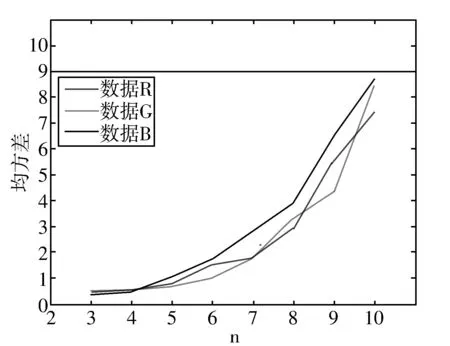
图6 均方差折线图

图7 PSNR折线图

从图6和图7中可以明显地看出，随着嵌入率的提高，PSNR逐渐减小。但减小的速度较为缓慢，当n=10即嵌入率为3.333 bpp时，PSNR仍大于38 dB，具有非常理想的图像视觉质量。另一方面，均方差随着嵌入率提高增长的速率也非常缓慢。当n=10即嵌入率为3.333 bpp时，均方差约在7～9之间，也就是说每个像素点的平均修改量约为2～3之间。因此可以说明该算法在提供较大嵌入率的同时，还能保证含密图像达到比较好的图像质量。

为了进一步体现本文算法的优越性，将本文算法与其他经典的算法进行比较。在相同的50幅图像下，计算LSBs、OPAP[3]、EMD[10]、FEMD[17]等算法处理后的图像峰值信噪比，与本文算法生成的峰值信噪比进行对比，具体如表2所示。

表2 不同算法在不同嵌入率下的PSNR比较

从表2可以明显看出，本文算法在嵌入率相同的情况下，PSNB明显大于同类的算法。

4.2.2 抗分析能力

抗分析能力也是隐写算法安全性能的一个重要指标。不同的隐写分析方法针对的方向不同，采取的分析依据也不尽相同。其中，直方图就是一个常用的分析依据，本文主要以此对算法进行分析。

直方图是以柱状图的形式表示图像的颜色分布情况。正常来说，图像的颜色分布变化是较为圆滑的，在直方图上可以看作为光滑曲线，而若经过处理后的图像颜色分布被破坏，直方图显示为毛刺状。

以baboon的数据R为例，分别取n=5、n=7、n=10，对图像进行满嵌入隐写，对生成的图像制作其直方图，如图8所示。

从图8可以看出，原图像的直方图较为光滑，隐写图像在n=5和n=7时都没有太大的差别，甚至在n=10的时候只出现细微的变化，并不存在毛刺状的情况，因此能够有效抵抗隐写分析。

5 结束语

本文通过对模运算、RGB特点以及彩色图像隐写方法的研究，提出了一种新型的模运算彩色图像隐写算法。本文算法中，引入一种隐写函数，并计算隐写函数的隐写系数，根据RGB数据的特点改变原始三维数据，以达到秘密信息安全嵌入的目的。同时，本文算法将二进制数转化成2n进制数，一方面提高了算法复杂度，保证其安全性，另一方面有效地增大了嵌入容量。大量的实验表明，该算法在大容量嵌入(嵌入率大于3 bpp)的情况下还能保证良好的安全性。为了降低本文算法的时间复杂度，进一步提高该算法的抗干扰性及抗分析性，本文下一步将研究自适应修改像素值，或选择自适应位置嵌入算法。