基于遗传算法的自抗扰控制器参数整定

干练 秦琨 陈赞 刘露 惠小博

摘要：自抗擾控制器具有超调小、响应速度快、抗扰能力强等优点。但是迄今为止，在参数整定问题上，仍然没有统一的有效的理论作支撑。本文基于遗传算法，将参数整定转化为多约束非线性规划问题并求解。最后，基于某型仿真转台，仿真验证了此种参数整定方法的有效性。

关键词：自抗扰控制器；遗传算法；参数整定；转台控制

中图分类号：TM7 文献标识码：A 文章编号：1007-9416（2018）06-0140-02

自抗扰控制（ADRC）算法实现简单，缺点是在非线性稳定性以及参数整定方面存在盲区[1]。近年来，随着计算机技术的发展，涌现出了一批人工智能随机搜索算法[2]。本文以具有代表性的智能算法为例，探索其在自抗扰控制器参数整定方面的应用。

1 自抗扰控制器的结构

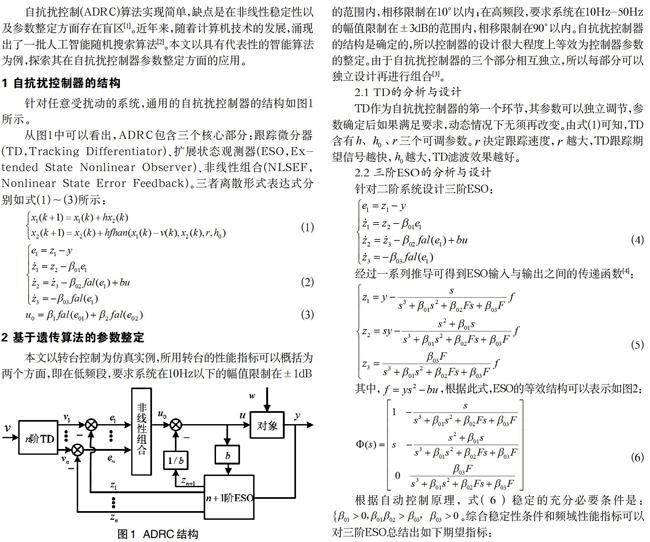
针对任意受扰动的系统，通用的自抗扰控制器的结构如图1所示。

从图1中可以看出，ADRC包含三个核心部分：跟踪微分器（TD，Tracking Differentiator）、扩展状态观测器（ESO，Extended State Nonlinear Observer）、非线性组合（NLSEF，Nonlinear State Error Feedback）。三者离散形式表达式分别如式（1）～（3）所示：

2 基于遗传算法的参数整定

本文以转台控制为仿真实例，所用转台的性能指标可以概括为两个方面，即在低频段，要求系统在10Hz以下的幅值限制在±1db的范围内，相移限制在10°以内；在高频段，要求系统在10Hz-50Hz的幅值限制在±3db的范围内，相移限制在90°以内。自抗扰控制器的结构是确定的，所以控制器的设计很大程度上等效为控制器参数的整定。由于自抗扰控制器的三个部分相互独立，所以每部分可以独立设计再进行组合[3]。

2.1 TD的分析与设计

TD作为自抗扰控制器的第一个环节，其参数可以独立调节，参数确定后如果满足要求，动态情况下无须再改变。由式（1）可知，TD含有三个可调参数。决定跟踪速度，越大，TD跟踪期望信号越快，越大，TD滤波效果越好。

2.2 三阶ESO的分析与设计

迭代结束条件取为超过连续500次不进化则算法停止，经过重复运行多次，目标函数收敛到0.24，ESO最优参数组合为：。

2.3 NLSEF的分析与设计

在ESO性能优良的前提下， NLSEF的设计类似于ESO的设计，同样需要考虑稳定性和性能两个方面。根据图1推导系统闭环传递函数，结果为：。

根据自动控制原理闭环系统稳定的充分必要条件为：。类似于ESO，将系统对稳定性以及性能的总体要求概括为约束条件，再次利用遗传算法求解找出一组满足要求的参数：。

3 控制器设计的实物验证

本文所使用的转台模型为：

将上文设计的控制器应用于此模型，取指令为正弦信号，电机力矩干扰为。将系统离散化后进行仿真，仿真结果如图3所示：

图3和图4表明，此组参数能够使系统很好地跟踪期望信号。低频段时，ESO能够准确的观测出系统的位置、速度以及综合扰动。位置速度误差都是收敛的，系统是稳定的。因此，依据本文方法设计的自抗扰控制器是有效的。

4 结语

本文受遗传算法的启发，提出了一种新的自抗扰控制器参数整定方法，并通过对转台系统的仿真控制验证了此方法的有效性，具有一定的借鉴意义。

参考文献

[1]赵志良.非线性自抗扰控制的收敛性[D].中国科学技术大学，2012.

[2]雷英杰.MATLAB遗传算法工具箱及应用[M].西安电子科技大学出版社，2014.

[3]赵海香.自抗扰控制器的优化设计与应用[D].哈尔滨工业大学，2013.

[4]H. Liu， S. Li. Speed control for PMSM servo system using predictive functional control and extended state observer[J].IEEE Transactions on Industrial Electronics，2012，59（2）：1171-1183.

Abstract：Active disturbance Rejection Controler（ADRC） has many advantages such as small overshoot， fast response， strong anti-interference capability and so on. But till now， One unified effective theory to describe parameters setting is still missing. In this paper， based on the genetic algorithm， we present that the conditions can be translated to the problems of multi-constraint nonlinear programming and then can be solved by finding an optimal objective function. At last， the simulation application in turntable proved the effectiveness of this method.

Key words：Self-rejection controller； Genetic algorithm； Parameter setting； Turntable control