空调压缩机转子系统动力学特性分析

高文栋 薛玮飞

广东美的制冷设备有限公司 广东佛山 528311

滚动转子式压缩机在空调、冰箱等制冷设备中得到广泛的应用。随着滚动转子压缩机的发展，对压缩机的整体性能要求逐渐提高，由于压缩机属于旋转类机器，在压缩机运行过程中，转子系统不停旋转运动，进而产生振动噪声，引起空调的振动噪声。

滚动转子式压缩机的转子系统是滚动转子压缩机的重要组成部分，转子系统的振动特性对于压缩机整机性能影响很大。目前，国外学者对压缩机振动和噪声研究比较广泛，日本学者通过分析噪音源，增加消音器，从而达到降噪的目的[1]；Katsumi Okada通过对压缩机转子运动轨迹，采用有限元差分法简化Reynolds方程，来计算转子轴心轨迹，从而对转子偏心结构进行改进[2]；美国普渡大学Kim和W.Soedel对压缩机消音器的传递参数进行了相关计算分析[3]；乐建波基于声学理论基础，构建消音器的物理模型和数学模型，采用数值模拟的方法，计算出消音器的传递特性并制定出消声器结构的声学优化方案[4]。国内研究主要集中在减振降噪以及噪音辨识方面，舒歌群等人对滚动转子压缩机机的结构进行相关分析，认为压缩机噪音主要分为电磁噪声、机械噪声、气流噪声，通过对压缩机噪声频谱图进行相关分析确定噪声源[5]。综上所述，国内外学者对于压缩机的研究主要集中在提高压缩机效率和变频控制方法上，对于振动噪声问题研究相对较少，对滚动转子式压缩机转子系统振动特性缺乏研究。

1 压缩机转子系统动力学方程

滚动转子压缩机泵体主要由滚动转子、气缸、滑片以及支撑弹簧、偏心曲轴和上、下轴承组成，滚动活塞被安装在偏心曲轴上，偏心曲轴机构主要包括滚动活塞、叶片弹簧系统，上下轴承。下轴承、气缸和上螺栓固定在一起，由气缸与壳体焊接，保持固定，滚动活塞和曲轴等运动件由上下轴承限制其位移。

有限元法的基本思想是将连续的求解区域离散成一组有限多个且按一定方式互联的单元组合。把压缩机转子等效为离散的Euler梁单元，其单元结构如图1所示。

离散化的梁单元内部位移向量可以表示为：

{ae}={x θyy -θx}T，其单元内插值函数可以表示为：N=[N1N2N3N4]。

其中，

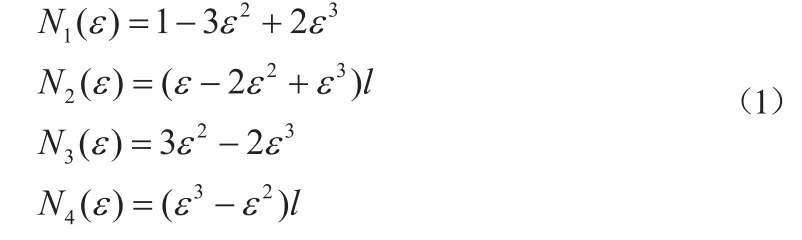
单元的质量矩阵、刚度矩阵和陀螺力矩阵分别为：

对压缩机转子受力分析，其受力情况如图2所示。

采用有限元法，建立压缩机转子系统的动力学方程如下：

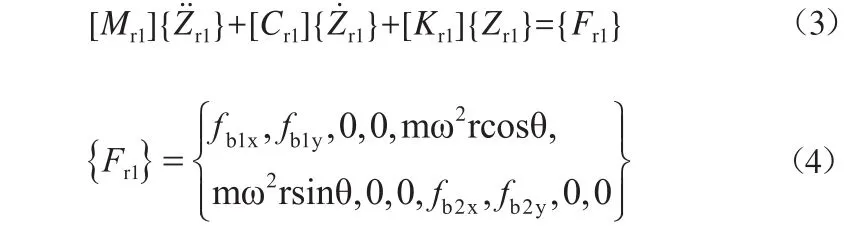
为转子的轴承、不平衡力和联轴器作用结点所受到的作用力。

对b1r、b2r结点，受到滑动轴承支承力为：

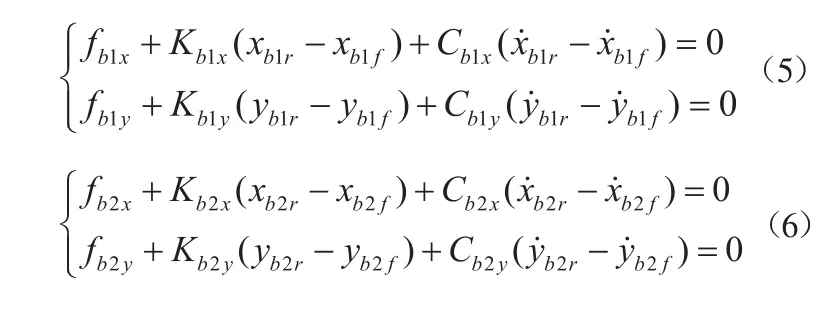
2 压缩机转子系统固有特性分析

图1 Euler梁单元示意图

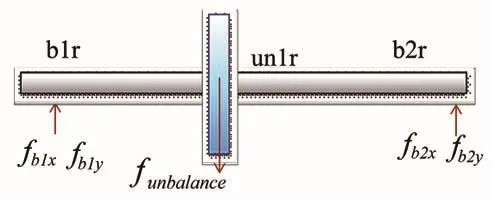
图2 转子1受力分析

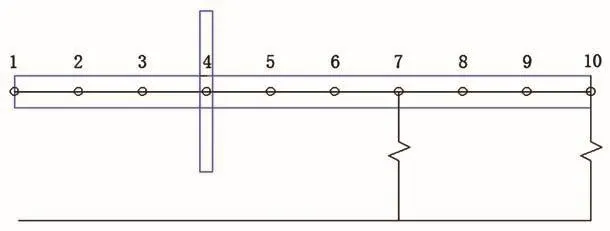
图3 压缩机转子系统结构示意图

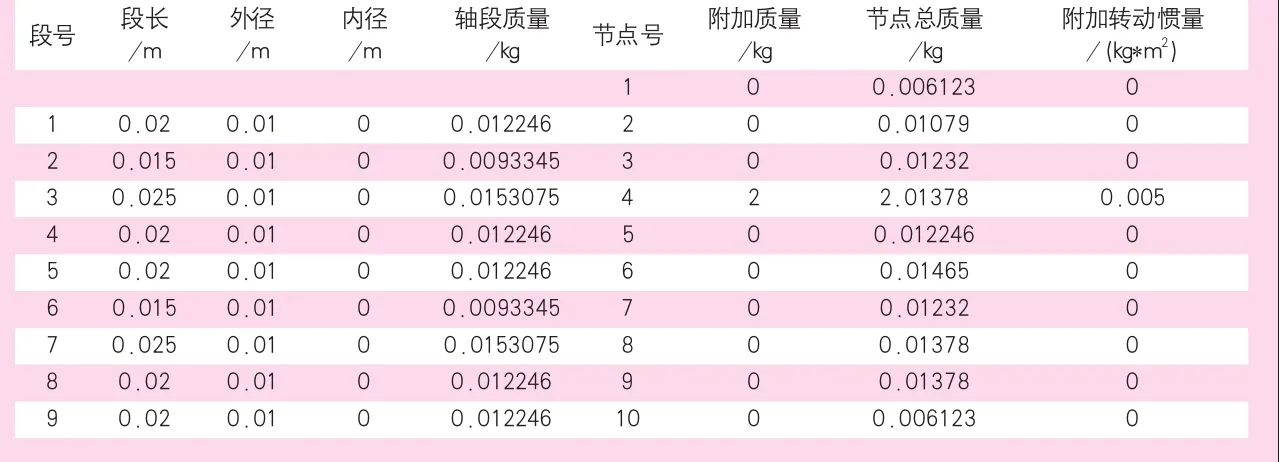
表1 各段结构参数

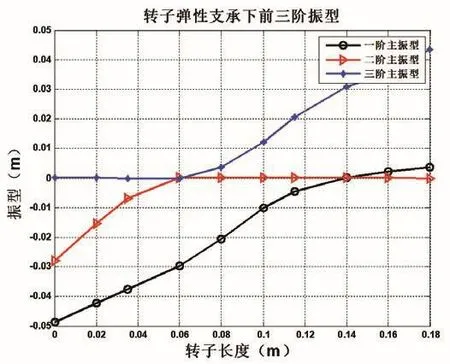
图4 转子系统前三阶振型

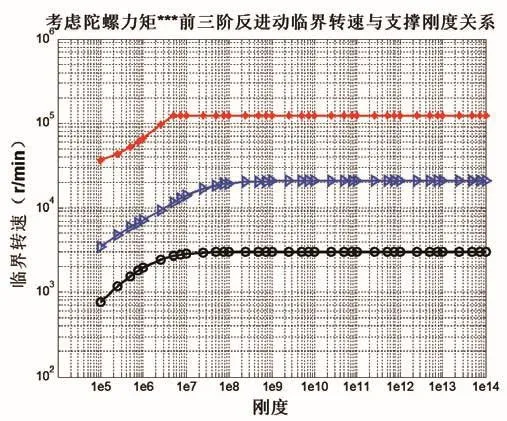
图5 转子临界转速与支撑刚度关系

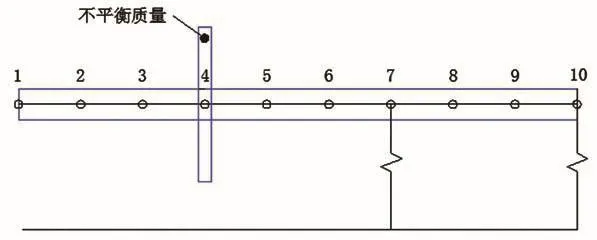
图6 压缩机转子不平衡响应设定不平衡量示意图

根据压缩机转子系统系统结构建立其有限元模型，如图3所示，其中定子部分采用集中质量单元和弹簧单元进行等效替代，转子系统部分划分为9个单元轴段，10个节点，共计40个自由度（每个节点4个自由度，不计轴向自由度），其中节点7和10采用弹簧单元，来模拟轴承以及定子和转子之间电磁力刚度，节点4为集中质量单元，模拟曲柄轴等偏心结构。转子系统各轴段的结构参数如表1所示。

在本算例中，节点7/10处的轴承刚度分别为1e7kg/m、1e7kg/m，转子杨氏模量为2.06×1011，泊松比为0.3，密度为7×103kg/m3，运用MATLAB数值程序计算，采用New-mark数值积分法，采用QR分解法求解系统的临界转速对压缩机转子系统进行动力学分析，转子振型及临界转速与支撑刚度关系如图4和图5所示。

采用有限元软件对压缩机转子系统仿真分析，采用压缩机转子系统结构进行等效处理，三维实体结构采用Solid45单元等效替代梁单元，弹簧单元采用combin214单元等效替代，集中质量采用Mass21单元等效替代，材料参数与刚度参数与上述相同，对压缩机转子系统三维模型进行动力学特性仿真分析，前三阶临界转速如表2所示。

通过转子系统固有特性对比分析可知，转子系统的有限元分析解与数值分析解前三阶数值误差控制在5%以内，从而验证了所建立的压缩机转子系统动力学模型的正确性，同时数值分析和有限元分析都能准确分析转子系统固有特性。

3 压缩机转子不平衡响应分析

对压缩机转子系统采用是New-mark数值分析法，对其不平衡响应进行相关分析，其假定在[t，t+Δt]时间段内，加速度为介于前后两时间点处加速度之间的某一常数。

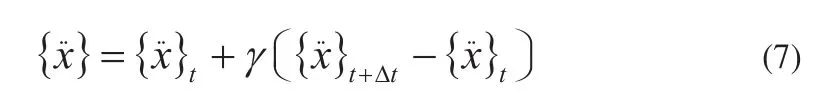
压缩机转子不平衡响应计算中不平衡量所在节点以及所观察的输出节点如图6所示，边界条件见表3。

在轮盘的偏心距离为0.00005m，偏心相位为90°，转速为3000rpm情况下，图7给出了刚性支撑下节点7的时间历程图，进一步保持转速和偏心相位不变，轮盘偏心距离增加10倍为0.0005m，图8给出了刚性支撑下节点7的时间历程图，通过图7和图8对比可知，偏心距增大10倍，对应的响应幅值增大10倍，因此可以得出转子系统轮盘的偏心量与其响应幅值呈线性关系。

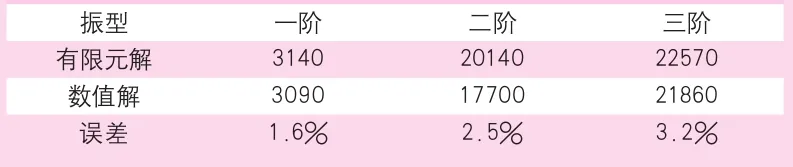
表2 临界转速对比分析

表3 压缩机转子系统响应特性计算边界条件

4 结论

通过对滚动转子压缩机转子系统结构进行相关简化分析，建立压缩机转子系统动力学模型，采用数值分析法和有限元法对压缩机转子系统固有特性仿真分析，同时对空调转子压缩机转子系统不平衡响应数值分析，主要结论如下：

（1）通过有限元法对压缩机转子系统进行动力学分析，把压缩机转子等效为离散的Euler梁单元，采用利用弹性力学有限元建立压缩机转子系统动力学方程；

（2）建立基于少自由度有限元法的压缩机转子系统动力学模型，运用MATLAB数值程序计算，采用New-mark数值积分法和ANSYS软件对压缩机转子系统固有特性进行分析，转子系统的有限元分析解与数值分析解前三阶数值误差控制在5%以内，从而验证了所建立的压缩机转子系统动力学模型的正确性，同时数值分析和有限元分析都能准确分析转子系统固有特性；

（3）采用New-mark数值积分法分析了不同偏心状态下的压缩机转子系统不平衡响应情况，分析结果表明转子系统中偏心量与响应幅值呈线性关系，通过压缩机偏心结构设计来降低压缩机振动具有一定的指导意义。

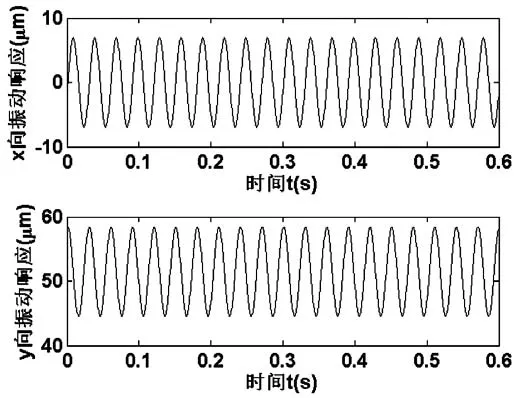
图7 偏心0.00005m状态节点7时间历程图

图8 偏心0.0005m状态节点7的时间历程图