基于SVM-ANN模型的滑坡易发性评价
——以三峡库区巫山县为例
夏 辉,殷坤龙,梁 鑫,马 飞
(1.中国地质大学(武汉),湖北 武汉 430074; 2.重庆市地质灾害防治中心,重庆 400015)
滑坡易发性评价是滑坡危险性评价以及风险评价的基础。滑坡易发性评价模型主要可分为确定性模型和非确定性模型,随着GIS技术的成熟和计算机的快速发展,基于统计分析的非确定性模型在区域滑坡易发性评价中应用越来越广泛,算法较为简单的有信息量模型[1]、证据权模型[2]、层次分析法[3]等,而随着大数据的发展,数据挖掘的兴起,一些较为复杂的算法也逐渐的应用到了滑坡易发性评价中,如决策树模型[4]、支持向量机模型[5]、人工神经网络[6]等。张俊等[7]利用信息量和logistic regression模型对万州区进行了滑坡易发性评价,并对比两个模型的预测精度,认为信息量模型的预测能力优于logistic regression模型。冯杭建等[8]在浙江淳安县对人工神经网络、逻辑回归和信息量三个模型在滑坡易发性评价中的应用进行对比,认为ANN模型优于其他两个模型。
本文以三峡库区巫山县为研究区,根据资料,提取指标因子,选取了支持向量机(SVM)和人工神经网络(ANN)模型对研究区进行了滑坡易发性评价,利用受试者工作特征曲线(ROC曲线)对两个模型的精度进行评价。然后,结合两个模型的易发性指数利用最大值法得到基于SVM-ANN模型的易发性区划结果,用历史滑坡点在高和极高易发区的占比对三个模型进行了对比分析。
1 滑坡易发性评价模型
1.1 支持向量机模型
假设支持向量分类的训练样本有n数据,其表示为[xi,yi](i=1,2……n),其中xi为输入变量(指标因子),yi为输出变量(是否为滑坡)。只考虑一个输入变量的情况下,支持向量回归的超平面形式为:
y=b+ωx
(1)
式中b为截距,ω为斜率。当有n个输入变量时,支持向量回归的超平面为:
(2)
式中WTX为ωixi的累积。在满足残差零均值和等方差的前提下,回归方程的参数估计通常采用最小二乘法,以输出变量的实际值与估计值之间的离差平方和最小为原则求解回归方程的参数,即求解损失函数达到最小值时的函数:
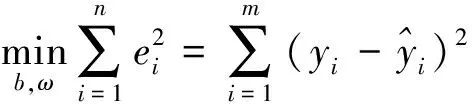
(3)
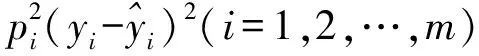
支持向量机采用ε-不敏感损失函数,回归分析中,每个观测的误差函数值都计入损失函数,而支持向量回归中,误差函数值小于ε,它给损失函数带来的损失将被忽略,不对损失函数做出贡献[9]。
1.2 人工神经网络模型
在ANN模型中,反向传播(B-P)训练算法是最常用的神经网络模型,也被认为是滑坡易发性评价中最有用的神经网络之一[10-11]。假设神经网络中输入xi,i=1,2,……,n(滑坡易发性评价中的指标因子),ωi表示其对应的权重(每个因子的权重)。取其特征函数为双曲正切函数,如下式:
(4)
(5)
式中,S表示神经元的输入总和;y表示神经元的输出;θ表示神经元的阈值。
B-P反向传播网络采用参数优化方法实现网络权值的调整。参数优化是在一个特定模型结构N中,采用数据D优化网络参数,目标是求得使损失函数L(W)=L(W|D,N)达到最小时的网络参数W。B-P反向传播网络的误差函数为Ep,用来衡量网络过程在输出层的表现能力,其表达式为:
(6)
式中,tpj表示网络实际输出;opj表示网络期望输出。
2 研究区概况
巫山县位于重庆市东部,地处长江三峡中下游。地理坐标为东经102°33′~110°11′,北纬30°46′~31°28′。南北长80.3 km,东西宽61.2 km,面积为2 958 km2,图1为研究区地理位置和灾害点分布图。
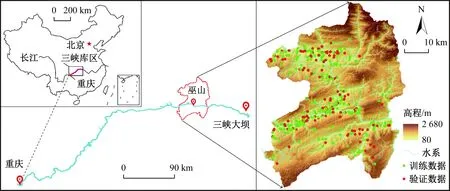
图1 研究区位置及地形图Fig.1 General situation of the study area
区内地形主要受巫山山脉和大巴山山脉的控制,地势南北高,中间低,地貌以中、低山为主,地形陡峭,沟谷发育。地处亚热带湿润气候区,四季分明,多年平均气温为18.4 ℃。县域地层属扬子地层区,地层岩性分布特征明显,中山区主要为三叠系嘉陵江组的碳酸盐岩夹泥岩,低山、丘陵区主要为三叠系巴东组的泥岩夹泥质灰岩,新生界第四系零星分布。巫山县内地质构造复杂,处于川鄂湘黔隆起褶带、大巴山弧和川东褶带的交界地带。长江横跨研究区,两岸支流水系发育,最大支流为大宁河流域。
在以上因素以及降雨、人类工程活动作用下,县域内地质灾害发育。根据三峡工程后续规划群测群防预警工程的统计资料显示,该区域内发育地质灾害共431处,其中滑坡396处,约占总数的91.9%。
3 指标因子的构建
本文进行滑坡易发性评价的数据来源包括:(1)巫山县地质灾害点排查资料;(2)巫山县1∶10 000地形图;(3)巫山县1∶20 000地质图;(4)分辨率为30 m的Landsat5 TM遥感影像。根据研究区的大小和滑坡的规模,本文采用分辨率为50 m×50 m的栅格作为滑坡易发性评价的基本单元。
3.1 因子的选取
通过整理筛选地质灾害点排查资料,利用ArcGIS转化得到滑坡灾害点分布图层。利用ArcGIS处理地形图,得到高程、坡度、坡向以及水系分布。将DEM数据导入SAGA-GIS,得到地形湿度指数(TWI)、地表粗糙度指数(TRI)。利用地质图提取到研究区地层岩性和构造分布,其中对不同地层的岩性进行分类,研究区主要分为5类岩性:页岩、泥岩、碳酸盐岩、石英砂岩以及第四系冲积物。对水系和构造带进行缓冲区分析,其中水系缓冲距离设置为:0~200 m, 200~400 m, 400~600 m, 600~800 m, 800~1 000 m, >1 000 m;构造带缓冲距离设置为:0~500 m, 500~1 000 m, 1 000~1 500 m, 1 500~2 000 m, 2 000~2 500 m, >2 500 m。在地理空间数据云网站收集到巫山县Landsat5 TM遥感影像,利用ENVI软件处理得到研究区归一化的植被覆盖指数(NDVI),并导入到ArcGIS中进行重采样得到分辨率为50 m的NDVI栅格图层。
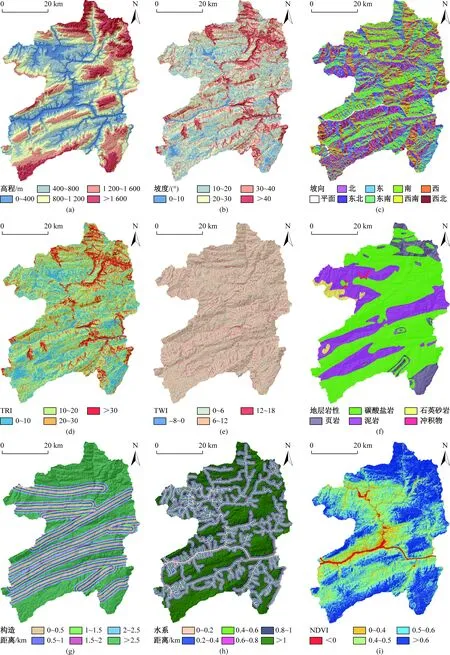
图2 滑坡易发性评价指标及其定量分类区划图Fig.2 Controlling factors of landslide susceptibility assessment
3.2 因子相关性分析
以上选取用于滑坡易发性评价的指标因子,与滑坡的发生均具有一定的相关性,但是各因子之间也可能存在某种相关性,如果将相关性较高的因子带入模型计算,会增加模型的复杂度和运行时间。因此,在模型计算之前,对各因子进行相关性分析,剔除与其他因子相关性较高的因子,能够有效地简化模型,提高模型的效率。将栅格化的各图层数据导入SPSS,利用其相关性分析工具得到各因子间的Spearman相关性系数(表1)和显著性水平Sig.值,Sig.值≤0.05表明各因子间的相关性具有显著的参考价值,|R|≤0.3表明因子间相关性微弱或不具有相关性[7]。高程和水系、NDVI的相关性系数大于0.3,因此剔除高程这一指标因子,其余的8类因子构成了巫山县滑坡易发性评价的指标因子体系(图2)。
4 滑坡易发性评价
4.1 基于SVM、ANN模型的评价结果
将滑坡灾害点图层和8类指标因子图层利用栅格转点工具得到研究区滑坡易发性评价数据库。选取灾害点和与其相等非灾害点数据作为样本,其中,灾害点随机分为2类:70%的灾害点(277个滑坡)作为训练数据,30%的灾害点(119个滑坡)作为验证数据。将样本数据导入SPSS Modeler进行训练,得到基于支持向量机和人工神经网络的易发性评价模型,然后将研究区总数据带入模型中计算,得到了研究区的滑坡易发性指数。将滑坡易发性指数导入ArcGIS,并利用自然断点法将研究区易发性指数分为5个等级,从而将研究区分为:极低易发区、低易发区、中易发区、高易发区和极高易发区,得到基于SVM和ANN模型的研究区滑坡易发性评价区划图(图3、图4)。
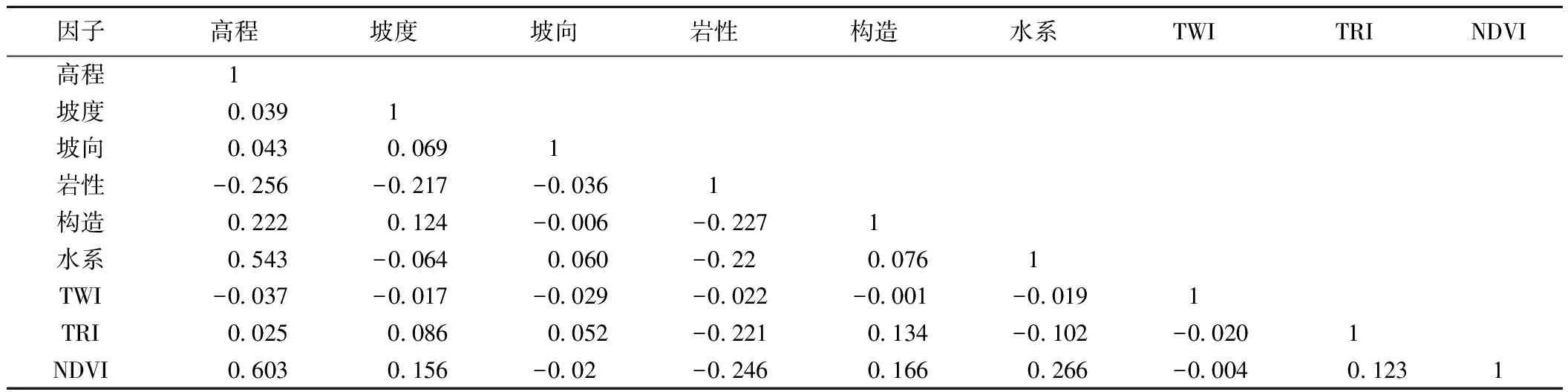
表1 指标因子相关性及其定量分类区划图Table 1 The correlation coefficient of controlling factor
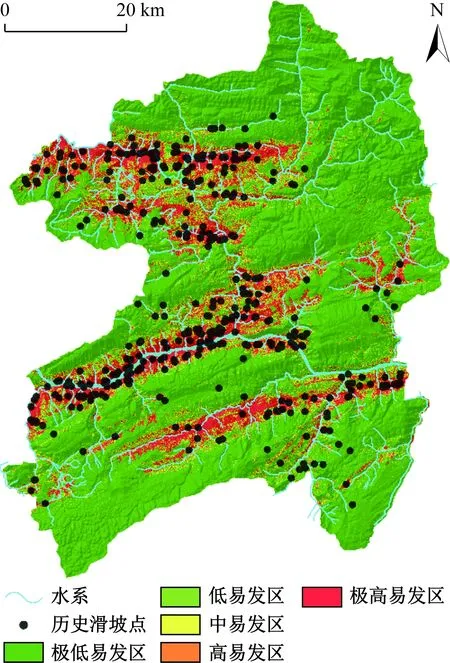
图3 基于SVM的滑坡易发性评价区划图Fig.3 Landslide susceptibility map based on SVM
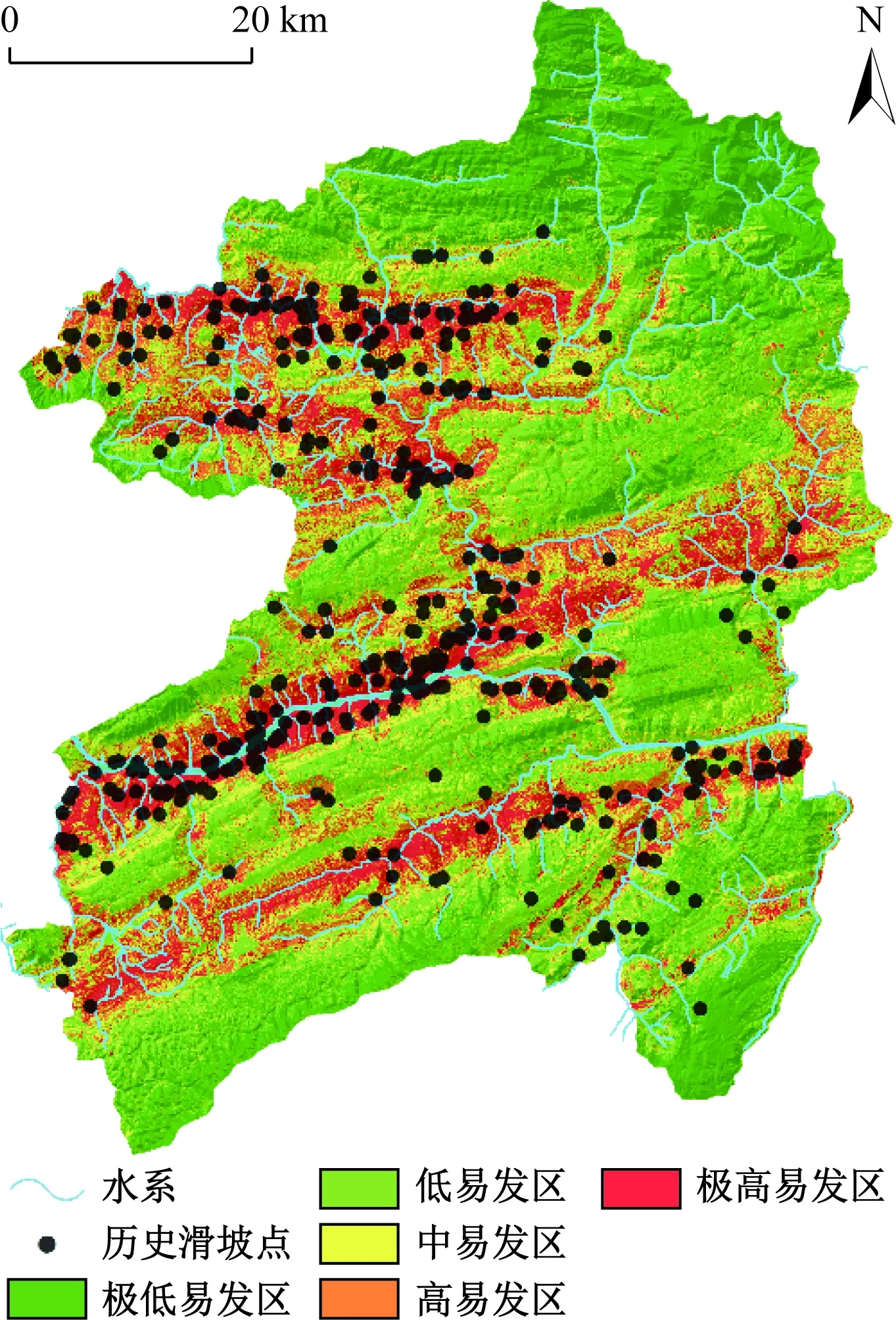
图4 基于ANN的滑坡易发性评价区划图Fig.4 Landslide susceptibility map based on ANN
本文利用受试者工作特征曲线对模型的精确性进行评价,在滑坡易发性评价中,ROC曲线的X轴为滑坡易发性指数,Y为滑坡累计发生频率。曲线下的面积(AUC)代表了模型精确性的大小,AUC值越接近于1,表明模型的精确性越高[12]。其中,由训练数据得到的ROC曲线为成功率曲线,验证数据得到的曲线为预测率曲线。通过SPSS数据分析,得到SVM和ANN模型的成功率和预测率曲线(图5、图6),SVM模型的成功率值为0.919、预测率值为0.862,ANN模型的成功率值为0.860、预测值为0.837。两个模型的AUC值均大于0.7,表明SVM和ANN模型在该研究区的滑坡易发性评价中预测能力均很好,且SVM模型预测能力略优于ANN模型。
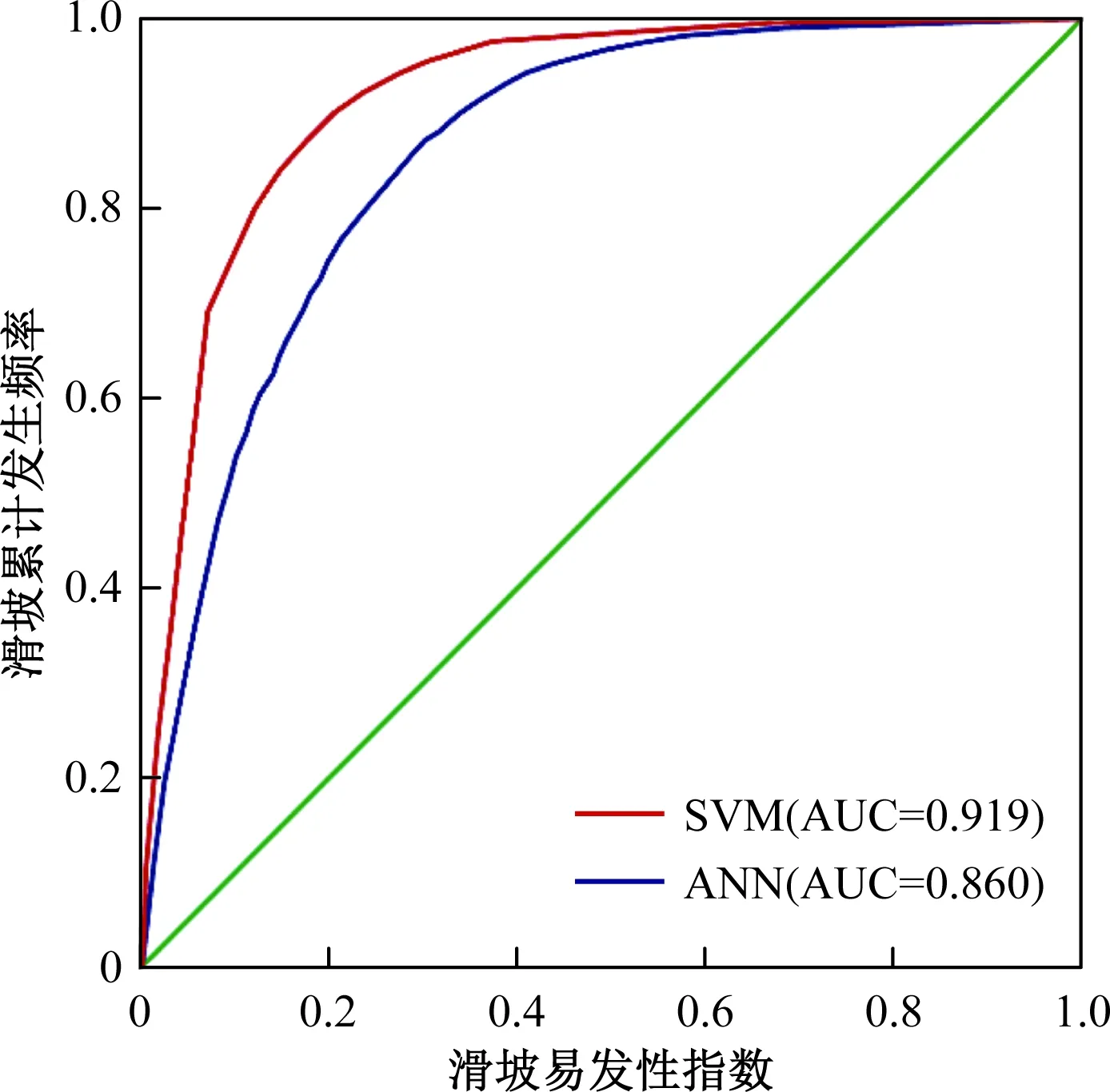
图5 模型成功率曲线Fig.5 The success rate curve of models
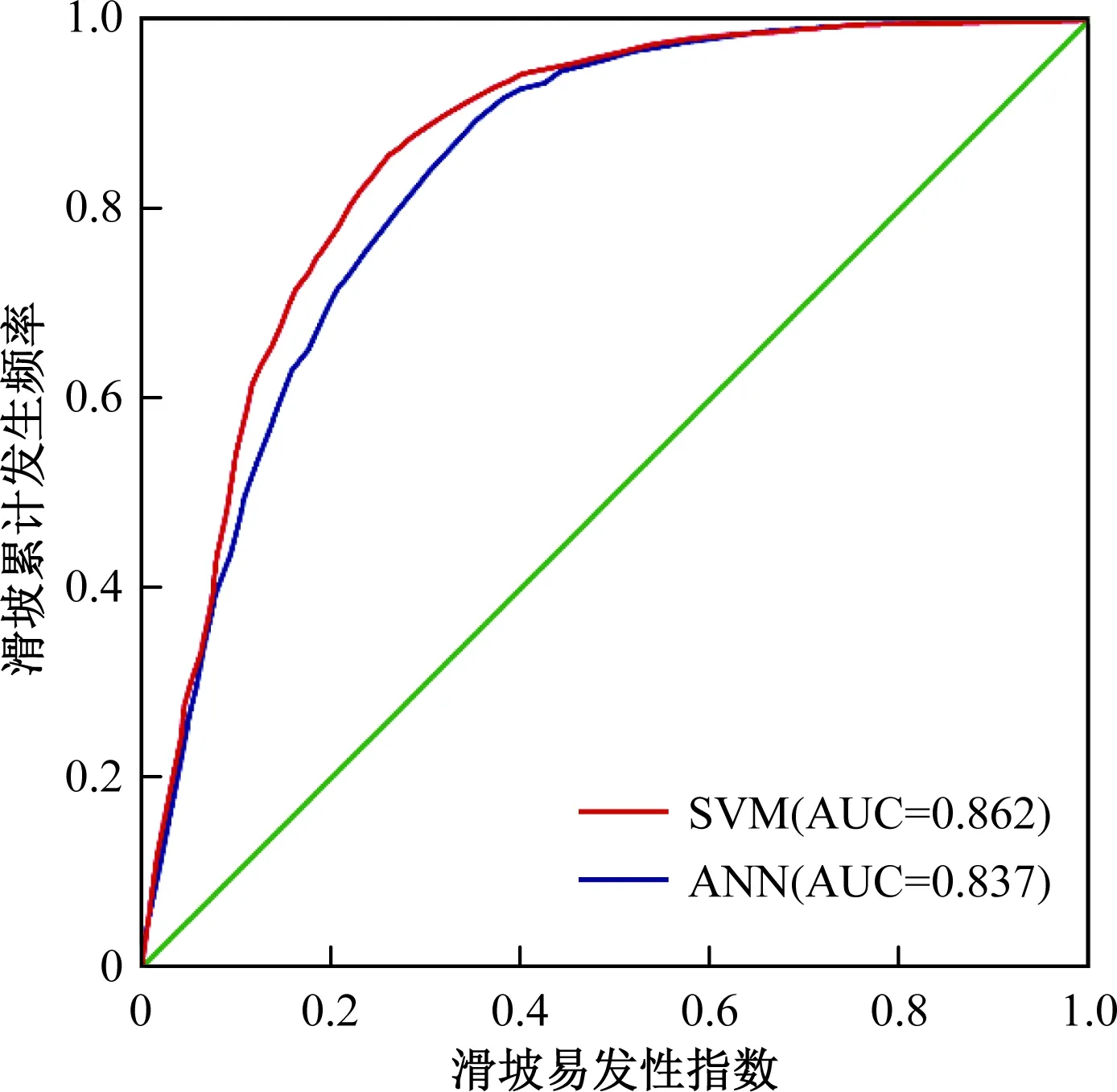
图6 模型预测率曲线Fig.6 The prediction rate curve of models
4.2 SVM、ANN结合的滑坡易发性评价
由SVM和ANN模型计算得到的滑坡易发性评价的精确度均较高,两个模型得到的易发性区划图中高易发区和极高易发区分布相近,但是存在某些小区域在SVM模型中属于极低和低易发区,而在ANN模型中属于中易发区,甚至高或极高易发区。在滑坡预警中,应秉承的理念是即使在区域进行了预警,滑坡没有发生,也不能滑坡发生了没有预警。基于这种理念,本文将两个模型计算得到的每个栅格滑坡易发性指数对比,取该栅格上滑坡易发性指数的较大值,其关系式如下:
LSI=Max(LSISVM;LSIANN)
(7)
式中,LSI表示滑坡易发性指数,Max函数表示取两者间的最大值。将式7计算的滑坡易发性指数导入ArcGIS,得到基于SVM-ANN的研究区滑坡易发性评价区划图(图7)。

图7 基于SVM-ANN的滑坡易发性评价区划图Fig.7 Landslide susceptibility map based on SVM-ANN
根据滑坡易发性评价结果,分别统计各易发性等级下历史滑坡灾害点栅格数以及所占比例(图8)。在SVM、ANN和SVM-ANN模型的结果中,历史滑坡点在高-极高易发区所占的比例分别为90.06%、83.18%和94.01%,表明基于Max{LSI(SVM);LSI(ANN)}函数的SVM-ANN模型能够提高SVM和ANN单一模型的精确度,其更适用于滑坡灾害风险分析的实际应用。
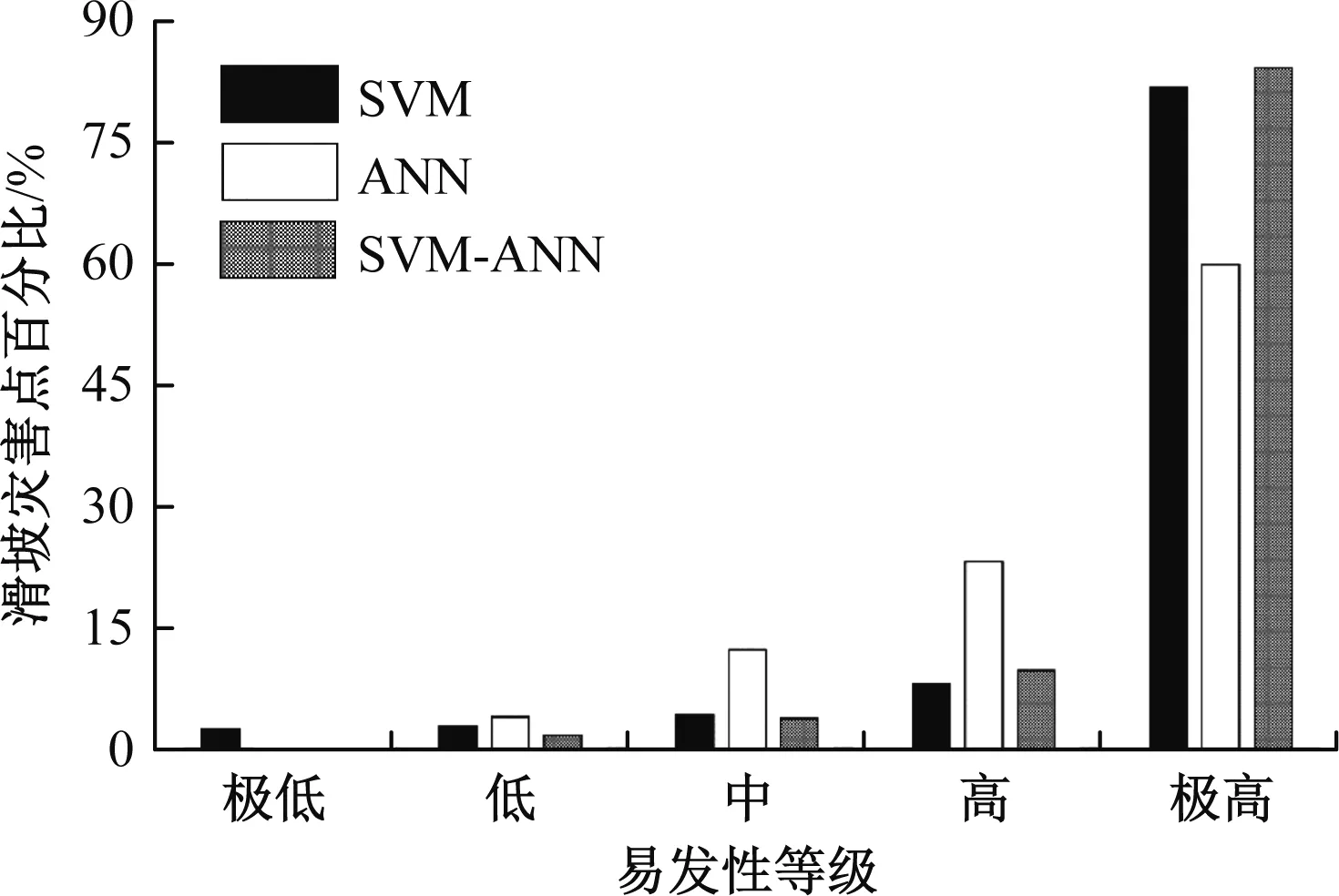
图8 各易发区历史滑坡点所占比例Fig.8 Percentages of landslide points falling into different susceptibility zonation
4.3 易发性分区结果分析
综合分析三种模型得到的滑坡易发性评价区划图,其结果表明,研究区高和极高易发区主要分布在长江及其支流大宁河与三叠系巴东组的泥岩夹泥质灰岩交汇,以及植被相对缺乏(NDVI值较小)的地带,并随研究区内向斜(大昌-水口向斜、巴雾河向斜、巫山向斜和官渡向斜)呈条带状分布。极低和低易发区主要分布在泥盆系、石炭系和三叠系下统的盐酸盐岩地区,海拔较高,植被发育。结果与历史滑坡灾害点分布相对一致。
5 结论
(1)本文以三峡库区巫山县为研究区,基于因子相关性分析,选取了坡度、坡向、TRI、TWI、地层岩性、水系距离、构造距离和NDVI共8类指标因子,结合历史滑坡灾害点数据,基于SVM和ANN模型利用ArcGIS软件对研究区进行滑坡易发性评价,得到研究区不同模型的滑坡易发性评价区划图。通过SPSS得到两个模型的ROC曲线,SVM模型的成功率和预测率曲线的AUC值分别为0.919和0.862,ANN模型分别为0.86和0.837,表明两个模型在研究区滑坡易发性评价的精度均较高。
(2)结合SVM和ANN模型评价结果,提出基于Max{LSI(SVM);LSI(ANN)}函数的SVM-ANN模型,并应用于研究区的滑坡易发性评价。通过统计,SVM、ANN和SVM-ANN模型中,历史滑坡点在高-极高易发区所占的比例分别为90.06%、83.18%和94.01%,表明SVM-ANN模型更适用于滑坡灾害风险分析的实际应用,从而说明结合多个模型来提高滑坡易发性评价区划图的适用性是可行的。
(3)滑坡易发性评价区划图表明研究区高和极高易发区主要分布在三叠系巴东组的泥岩夹泥质灰岩与河流的交汇,且植被相对发育较弱的地带,随区内向斜呈条带状分布,与研究区实际情况相对一致,能够用于滑坡灾害危险性评价及风险评价中。
——重庆市农业广播电视学校巫山县分校

