再谈“错位相减法”*

安徽省合肥市第一中学 (230601)

刁海宝 时英雄

在高中数列的学习中，求和是最常见的问题，也可以说是数列题的精髓问题，其中一些求和方法比如：公式法、倒序相加法、错位相减法、裂项相消法、并项求和法等常用的方法需要老师在平时的教学中讲授透彻，如什么时候用？怎么用？易错点在哪？而学生在学习的过程中也要通过演练强化对方法的理解，使用的技巧等，这里笔者主要通过几例针对“错位相减法”的求和方法谈谈数列的教学，抛砖引玉，以飨读者.

1.使用错位相减法需注意的两点

错位相减法主要是针对差比型数列的求和，差比型数列即为等差数列的项与等比数列的项对应相乘后构成的一个新数列，这种类型的数列在平时的教学及高考中都经常遇到，一般在解决此类问题时，将数列的前n项和写成展开形式，然后两边同乘以等比数列的公比或者是公比的倒数，接着错开位置后相减再利用等比数列求和公式整理即可，错位相减法关键是两点，一是位置一定要错开，二是后面等比数列求和化简，这种方法简单易上手，难点就是后面的化简整理容易出错.

例1 设等差数列{an}的前n项和为Sn，且S4=4S2，a2n=2an+1.

(1)求数列{an}的通项公式;

解：(1)易得an=2n-1,n∈N*.

2.错位相减法的公式计算方法

对于差比型数列求和，利用错位相减法将其一般化得到如下结论：

结论1[1]设数列{an}的通项公式为an=(an+b)qn-1(q≠1)则其前n项和Sn具有形式：

Sn=(An+B)qn+C，其中参数A,B,C满足：A(q-1)=a,B(q-1)+A=b,C=-B.

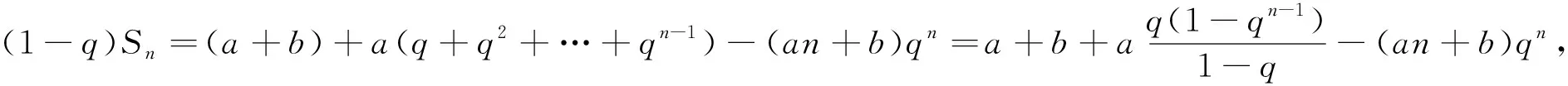
3.错位相减法用途的推广

例2 已知数列{an}的通项公式为an=n2·3n，求其前n项和Sn.

解：令Sn=12·31+22·32+32·33+…+n2·3n,3Sn=12·32+22·33+…+(n-1)2·3n+n2·3n+1,相减得-2Sn=1·31+3·32+5·33+…+(2n-1)·3n-n2·3n+1(*)

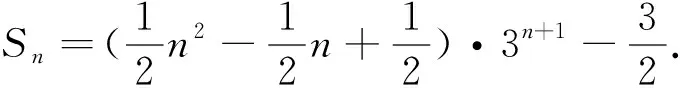
若数列{an}的通项公式an=f(n)qn(q≠0,q≠1)，其中f(n)=a0nm+a1nm-1+…+am-1n+am，a0,a1,…,am及m均为常数且m∈N*，求{an}的前n项和，可以结合二项式定理，通过m次错位相减将关于f(n)的多项式次数降次再转化为下一个错位相减，最终使问题获解，可见，错位相减法的实质就是降次、降次再降次，转化、转化再转化[2].

4.错位相减法的姊妹篇——错位相加法

解：Sn=a1+5a2+52a3+…+5n-1an(1),

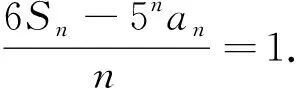
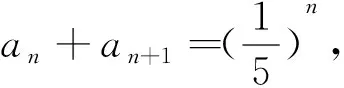
5.结束语

错位相减法是一个非常常见的求和方法，但在平时的教学中发现学生在用这个求和方法时经常算不出正确的答案，究其原因就是在使用时有的没有错位，有的在乘以公比或公比的倒数时乘的位置不对，有的同学忘了最后一项是减号等等，所以在教学时一定要让学生在解答时规范，按步骤来，理解什么时候用错位相减法，为什么可以这么做，本文将错位相减法加以类比、归纳，将其用途加以推广，又给出一般性的结论来帮助学生得出正确的结果，让学生在认识，了解，理解的基础上掌握此技能，并能将其延伸推广，所以在平时的教学中教师不光要把基本的知识传授给学生，如果自己能研究更深层次的话，高屋建瓴，对学生来说是大有裨益的.