Three-dimensional numerical study of flow characteristics and membrane fouling evolution in an enzymatic membrane reactor ＊

Xu-qu Hu (胡徐趣), Pai-qing Wu (吴排青), Xing-yi Wang (王星燚), Hai-cheng Zhang (张海成),Jian-quan Luo (罗建泉)

1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China

2. State Key Laboratory of Biochemical Engineering, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China

Abstract: In order to enhance the understanding of the membrane fouling mechanism, the hydrodynamics of the granular flow in a stirred enzymatic membrane reactor is numerically investigated in the present paper.A three-dimensional Euler-Euler model, coupled with the k-ε mixture turbulence model and the drag function proposed by Syamlal and OʼBrien (1989) for the interphase momentum exchange, is built to simulate the two-phase (fluid-solid) turbulent flow.Numerical simulations of single- or two-phase turbulent flows at various stirring speeds are carried out.The numerical results agree very well with the published experimental data.Results include the distributions of the velocity, the shear stress and the turbulent kinetic energy.It is shown that the increase of the stirring speed not only enlarges the circulation loops in the reactor, but also increases the shear stress on the membrane surface and accelerates the mixing process for the granular materials.The time evolution of the volumetric function of the granular materials on the membrane surface can qualitatively explain the evolution of the membrane fouling.

Key words: Turbulent flow, multiphase flow, membrane fouling

Introduction

The membrane technology, as one of the best energy-saving separation methods, is applied in various industrial processes, e.g., the wastewater treatment and the biological filtration.It is wellknown that the membrane fouling is a particularly important issue in constructing a sustainable and high-efficiency operation of the membrane technology.To reduce or to avoid the effect of the membrane fouling, many effective control strategies were proposed over the past decades, such as the membrane flushing[1], the gas sparging[2], the surface modification[3], and the high operating shear rate[4].The hydrodynamic properties have great impacts on the effect of the membrane fouling[5]The accurate predictions of the flow characteristics and the mass transfer are important in designing and evaluating the membrane systems[6].The membrane separation process in various membrane systems was extensively studied during the past decades[7].A widely investigated problem is the single-phase flow in the membrane system, which is fundamental and also very important for understanding the mechanism of the membrane fouling.Torras et al.[8]applied the commercial Computational Fluid Dynamics (CFD) software,Fluent, to investigate the flow characteristics in a rotating disk filtration membrane module with consideration of the effects of the flow rate, the rotation rate and the geometry.It is shown that the numerically predicted shear stress and pressure variation are in good agreement with the analytical solutions[9].Wang et al.[10]used a porous media approach to simulate the membrane structure in a submerged hollow fiber membrane bioreactor.The single-phase hydrodynamic properties were significantly improved by the use of porous media models.Jalilvand et al.[11]applied the porous media model in their numerical investigations of high cross-flows in the microfiltration process.The hydrodynamic properties (e.g., the permeate flux, the resistances and the shear forces) under various operating conditions were successfully predicted.Recently, Ameur et al.[12]numerically investigated the flow fields and the power consumption in a vessel stirred by a multistage impeller.They carefully studied the effects of the stirring rate, the fluid rheology, the vessel size and the impeller location on the performance of such stirred systems.The studies of the single-phase flow are of practical significance for the improvement of the membrane performance of various membrane systems.However, the feed solution flowing into the membrane systems is usually composed of multiple phases.

During the past decade, the research attention was increasingly paid to the numerical simulations of multi-phase flows in various reactors.Reza et al.[13]constructed a CFD model to solve the momentum and protein concentration continuity equations.The reversible and irreversible membrane fouling resistances were carefully examined in their study.Jong et al.[6]compared the numerical results obtained by using the Discrete Particle Model (DPM) and the two-fluid model (TFM) with the experimental results of a fluidized bed with flat membranes.Their numerical predictions of the bubble size distribution during the gas addition agree well with experimental results.Recently, Trad et al.[14]numerically studied the hydrodynamic characteristics and the mixing features of single-phase or two-phase flows in a submerged membrane bioreactor.A compromised operation mode was deduced from their CFD simulations, which was shown to be a balance mode between the prevention of the vortex formation and the promotion of the homogeneity degree.More numerical studies about the membrane performance can be found in Refs.[15-16].Despite the achievements of these studies in the understanding of the fouling mechanism,to the best of our knowledge, there are still relatively few studies of the membrane fouling evolution with consideration of multi-phase flows.

The present study focuses on the flow characteristics and the membrane fouling mechanism in a widely used enzymatic membrane reactor.A three-dimensional Euler-Euler model is built, coupled with thek-εmixture turbulence model and a classical drag function, to describe the two-phase turbulent flow.Firstly, the hydrodynamics of the fluid(single-phase) flow in a stirred reactor is numerically studied.The flow characteristics include the velocity distribution, the shear stress and the turbulent kinetic energy.Numerical simulations of the two-phase flow at various stirring speeds are then carried out to study the mixing process of the granular flow, focusing on the distributions of the granular materials on the membrane surface, for the understanding of the membrane fouling mechanism.

1.Methods and models

1.1 Problem description

Our study is based on a magnetically stirred dead-end cell (Amicon 8050, Millipore, USA), as is widely used in experiments of the membrane filtration and the enzymatic reaction[16].As shown in Fig.1(a), a flat membrane with an effective area of about 1 590 mm2(45 mm diameter) is fixed on the substructure of a cylindrical housing.An inverted T-shaped blade is placed near the membrane, which can be rotated with a shear rate on the membrane surface.Filling the cell with nitrogen gas can provide a nearly constant pressure.The feed solution is pressure-driven to flow towards the membrane surface.Because of the effect of the membrane filtration, the granular pollutants are separated from the feed solution and stay in the container.

Fig.1(a) Schematic diagram of the enzymatic membrane reactor

We assume that the feed solution is composed of multiple phases, with the main phase of water accounting for 99% volumetric fraction (φ), and the granular pollution material of density 2 000 kg/m3constituting the other 1% (secondary phase).The average diameter of granular material (Dp) is 0.05 mm.The ultrafiltration membrane settled at the end of the reactor is RC10-M or RC05-M (PLGC, Millipore,USA) in our study.The constant rotation speed of the T-shaped blade is assumed as 60, 150 and 250 revolutions per minute (rpm), respectively.

1.2 Euler-Euler approach

The feed solution consisting of a small amount of granular materials (1% in volumetric fraction)dispersed in the pure water is considered as an interpenetrating continuum.The Euler-Euler approach is widely applied for simulating the unsteady multiphase flow.The Euler-Euler multiphase approach in the present study takes the solid-solid momentum exchange into account, which cannot be neglected in a high-concentration mix flow.It is assumed that the two phases occupy different volumes of space and the Euler-Euler approach is applied to describe this two-phase (fluid-solid) solution.The subscriptiis used to distinguish the two phases from each other,withi=sfor the solid andi=lfor the liquid.The volumetric fractions of both phases (αi) are continuous functions of space and time, and their sum should be equal to one

As the solid materials take up only a very small fraction in the mixed phase, we define the liquid as the carrier phase.Both phases are modeled as a continuum.The governing equations for the mass conservation is

whereρanduare the density and the velocity,respectively.The governing equations for the momentum conservations can be written as:

wherepis the pressure,Fis the external forces acting on the systems, andKlsrepresents the interphase momentum exchange term.According to Newtonʼs law of viscosity, we can obtain the viscous stress tensor for both phases

whereμis the dynamic viscosity,is a unit

tensor, andis the strain rate tensor.For the phase of Newtonian fluid, the expansion viscosityλthat measures the difference between the thermodynamic and mechanical pressures is about three times larger thanμ, while it is zero for the solid phase according to the Stokesʼ assumption.Although there are many models for the dynamic viscosity of the solid phase,we have used the widely accepted one proposed by Luo et al.[17].It can be expressed as

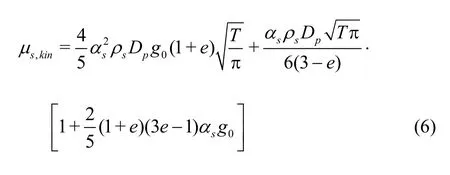
whereg0is the function of the radial distribution,Tis the thermodynamic temperature of the solid material, anderepresents the restitution coefficient.More details about the theory for the dynamic viscosity of the solid phase can be found in Ref.[14].

1.3 Interphase momentum exchange

For this granular flow, the fluid-solid interaction is mainly achieved through the momentum transfer between the two phases.The interphase momentum exchange term (Kls), which can be obtained by specifying the drag functions, is a key factor in the simulation of granular flows.In the present study, we apply the drag function proposed by Taghipour et al.[18], in which the correlation for the momentum exchange coefficients takes the following form

where the relativeReynolds numberResis defined as

The drag function for a single granular particleCDtakes the following form

The terminal velocity correlation for the solid phasevr,sis

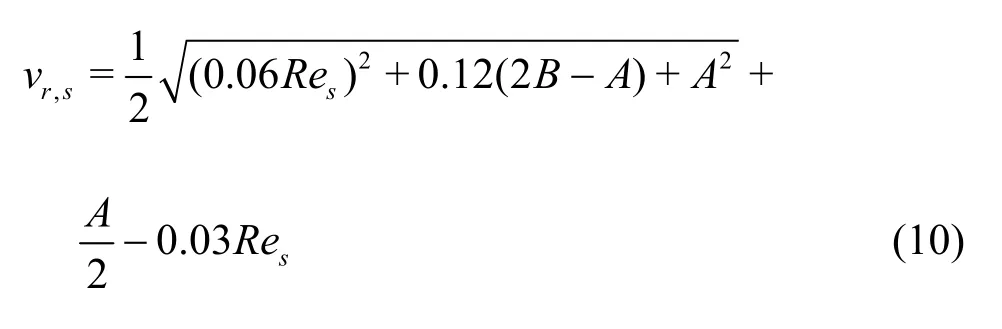
1.4 k-εmixture turbulence model

As the mixed phase is stirred by high-speed blade rotations, the Reynolds number for the flow in the reactor is relatively high.The effect of the turbulent flow should be taken into account in modeling[19-20].The standardk-εturbulence model, initially proposed by Launder and Spalding (1972), is based on two transport equations for the turbulence kinetic energy(k) and its dissipation rate ()ε.The model used for the numerical simulations of the turbulence flows is widely validated during the past several decades, e.g.,in Refs.[8, 21].We apply thek-εmixture turbulence model in the present study, which can be expressed as follows:

wheremρ,um,μt,m,Gk,mrepresent the density,the velocity, the turbulent viscosity and the production of the turbulence kinetic energy of the mixed phase,respectively.They are defined as follows:

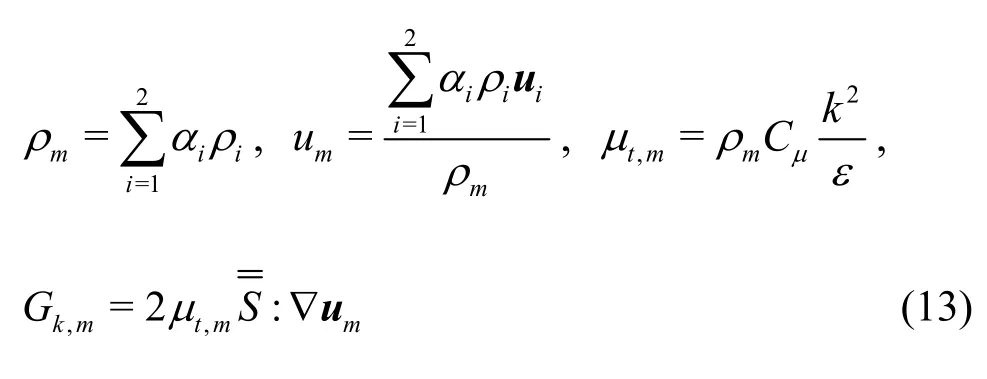
The other coefficients are set asC1ε= 1.44,C2ε=1.92,Cμ=0.09 andσk=1.3.They are all determined from experimental results, and the accuracy is validated for a wide range of turbulent flows[8,20].

1.5 Numerical implementation

We apply the multiple reference frame (MRF)approach to model the stirring blades.Under the moving frame, the flow around the stirring blade can be simplified as a steady-state problem[21].For the ultrafiltration membranes, we use the porous medium model to simulate its physical behavior that allows the water to pass through it but acts as a barrier for the granular particles.We set the porosity of the porous medium as 0.0001 so that the granular materials with diameters over 0.05 mm cannot penetrate through the membrane surface.The effect of the membrane resistance is described by the Darcyʼs law, for which the coefficients are derived from our experimental results.In the process of operations, we consider that a constant pressure (200 kPa) is applied at the inlet, and the outlet is acted with the atmospheric pressure.

As shown in Fig.1(b), the flow domain is discretized into a finite number of contiguous control volumes by an unstructured mesh of about 272 000 tetrahedral elements.These governing equations,which are discretized by the second-order upwind scheme, can be obtained from the finite volume method by the Fluent code.We have checked the influence of the mesh size using a mesh twice as small as that described above and have not found a significant influence on the results of the flux.In order to ensure the calculation precision, we have used a refined mesh at the region surrounding the blades.A time step of 0.001 s is applied for the time integration.

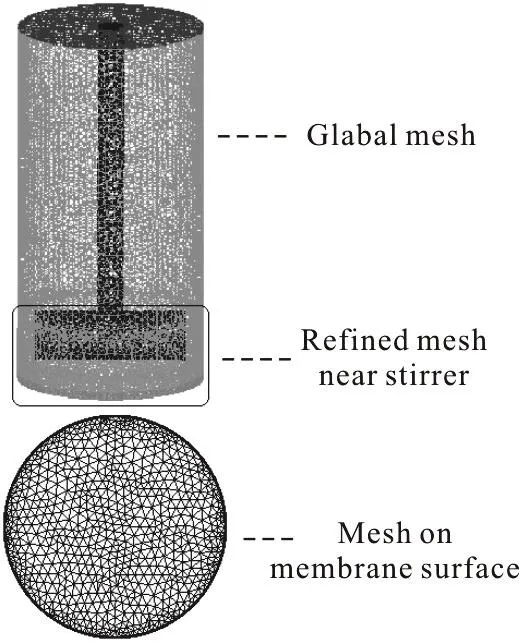
Fig.1(b) Schematic diagram of the corresponding mesh

1.6 Validation

The flux variation with respect to the transmembrane pressure (TMP) for many types of ultrafiltration membranes was experimentally investigated in our previous study[16].We found that, when the absorption fouling or the pore blocking is kept weak, the total filtration resistance remains constant and the flux increases linearly with the TMP.The flux,as a linear function of the TMP, can be a good reference for the validation of numerical models.The pressure-driven water flow is studied in a non-stirred reactor to validate our numerical model.The flux predicted by the present numerical model is compared with the published experimental data[17]in Fig.2.The numerical and experimental results are found in a good agreement for both RC10-M and RC05-M membranes.This implies that our numerical models,as well as the porous medium approach that we use,are suitable and accurate for modeling this membrane system.

Fig.2 Comparison of numerical and experimental results of flux (M)to transmembrane pressure

2.Results and discussions

We apply the numerical model to simulate the stirred complex flow in an enzymatic membrane reactor.The stirring speed takes values of 250 rpm,150 rpm and 60 rpm, respectively.We firstly study the single-phase flow of the pure water to examine the flow characteristics in a stirred reactor.The membrane fouling evolution is then studied by numerically simulating the granular flows, with the fluid-solid phases of 99% of the water and 1% of the granular solid particle as described above.The following results are all for the cases in the steady state.

2.1 Flow characteristics

As shown in Fig.3 (b), the flow velocity at the membrane center is much lower than that in the marginal area.The rotational speed of the fluid can be accelerated by increasing the stirring speed.In principle, a larger stirring speed can induce a higher shear rate, which makes the surface adhesion of the pollution material on the membrane harder to form[22].This result confirms the experimental fact that a higher stirring speed is often beneficial in controlling or reducing the effect of the membrane fouling[23].

The flow characteristics can greatly affect the separation efficiency of the membrane systems.In this section, we numerically study the single-phase flow in a stirred reactor.Figure 3 shows the velocity distributions on vertical and horizontal (i.e., membrane surface) planes.We can see that there are two obvious circulation loops on both sides of driven shaft, as is in a good agreement with previous experimental and numerical studies[14,20,24].These circulation loops are formed due to the vortex formation.With the blade rotations, the fluid around the blades is stirred, to be centrifuged towards the sidewall of the container.The radial jet is blocked by the wall boundary to be transformed to two main tributary flows: the upstream flow and the downstream one.Since the fluid is continuously pumped into the container, the upstream flow will meet the inlet flow in the middle of the container, to be merged to form a vortex.The vortex circulating near the shaft makes the circulation loops.It is of interest to notice in Fig.3 that, the area of the circulation loops can be significantly enlarged by the increase of the stirring speed.This implies that a higher stirring speed makes less flow concentration near the membrane, which is beneficial for preventing the membrane fouling.The downstream flow moves towards the base of the container.When it reaches the membrane surface, it is partially transformed to a permeating flow since the membrane is modeled as porous media.However, most of the flow stays inside the container and converges to the rotating flow on the membrane surface.Figure 4 shows the variation of the shear stress along a radial line on the membrane surface.The shear stress is relatively low in the central area, but it increases rapidly with the increase(or decrease) of the radial position.This radial non-uniformity of the shear stress is mainly caused by the inhomogeneous distribution of the velocity[25].As shown in Fig.3 (b), the velocity distribution at the membrane center sees a low velocity gradient, which is just the reason for the low shear stress.It is shown that the velocity gradient is negligible for a low stirring speed but notable for a high stirring speed.Accordingly, we can also find in Fig.4 that the increase of the stirring speed can significantly enlarge the shear stress on the membrane surface.

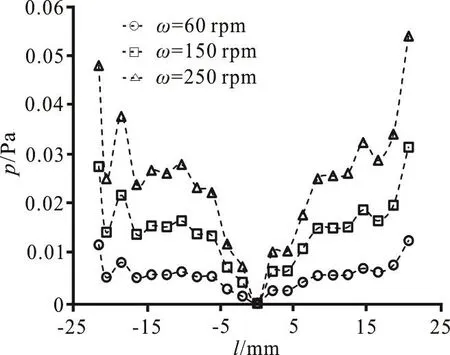
Fig.4 Variation of shear stress along a radial line (l) on membrane surface

Fig.5 (Color online) Distributions of turbulent kinetic energy(K) on a radial plane in the middle of the blade (z=15mm)

The distribution of the turbulent kinetic energy on a radial plane at the middle of the blade(z= 15mm) is shown in Fig.5.For the stirring speed of 250rpm, the turbulent kinetic energy near the blade tips is about 0.012 m2/s2, which is almost six times larger than that in the central area.It is because the flow speed in the gap between the blade tips and the wall boundary is relatively high, which inherently leads to a larger Reynolds number, and of course, a higher turbulence intensity near the blade tips.We can also find that the turbulent kinetic energy is nearly constant (0.004 m2/s2)in the marginal region.This result agrees well with the previous study of Taghipour and Ellis[18].The effect of the stirring speed is also significant on the distribution of the turbulent kinetic energy.At the stirring speed of 150 rpm, the turbulent kinetic energy is only about one half of that at the stirring speed of 250 rpm, and it decreases nearly to a constant value of about 0.002 m2/s2at the stirring speed of 60 rpm.This result implies that the turbulent intensity that is highly relevant to the mixing process and the membrane fouling can be significantly modified by the stirring speed.

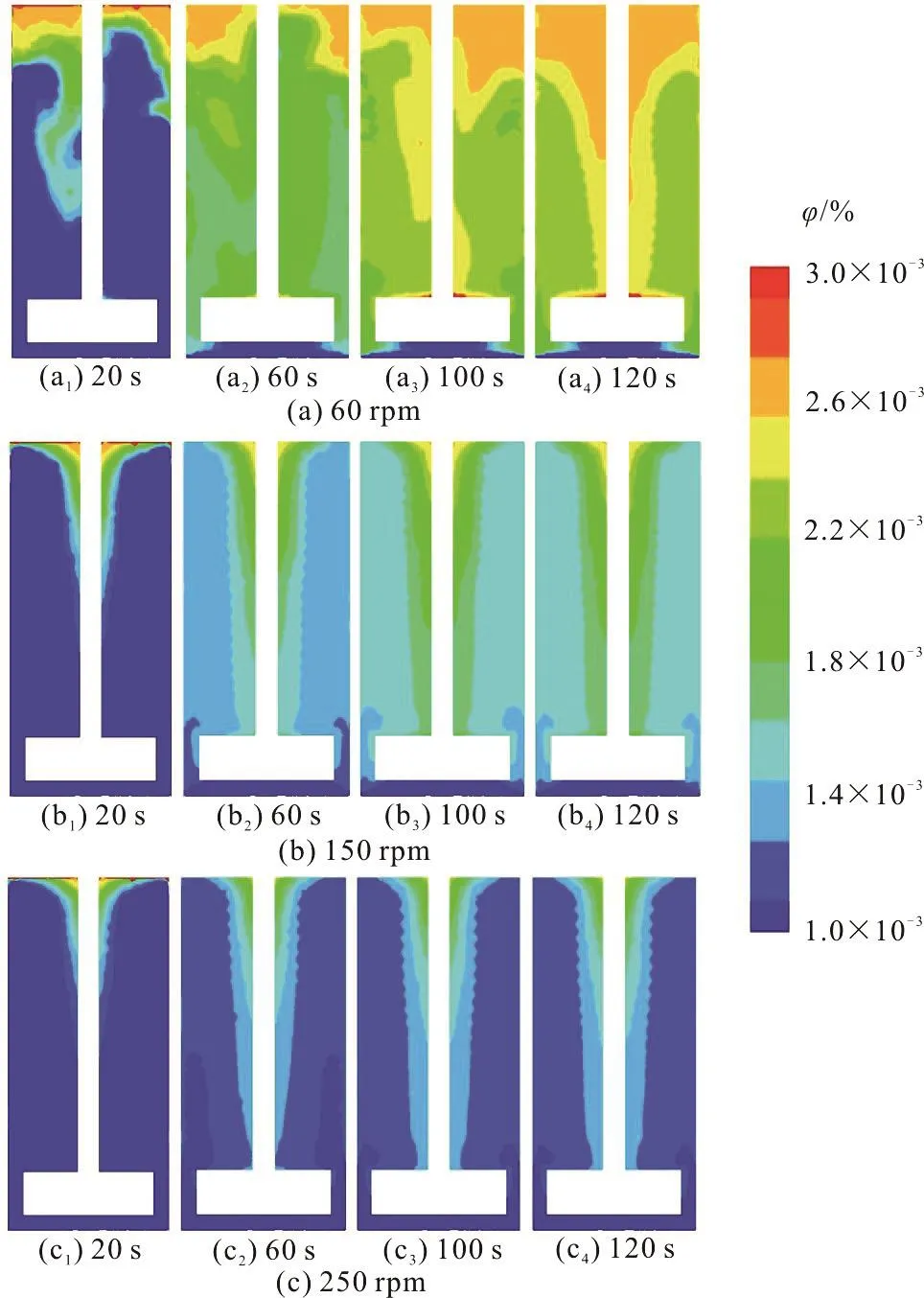
Fig.6 (Color online) Mixing evolutions of granular materials in a container at different stirring speeds

2.2 Membrane fouling evolution

The container is initially filled with the pure water.It is assumed that the feed solution is pumped into the container from the inlet at the beginning of the numerical simulations.The feed solution, consisting of a small amount (1% in volumetric fraction) of the granular materials dispersed in the pure water, is transported and mixed by the fluid flow in a well-stirred reactor.This granular (fluid-solid) flow is carefully investigated to reveal the mixing process of the pollutant materials and the evolution of the membrane fouling.The mixing process of the granular materials in a container at different stirring speeds is shown in Fig.6.The granular materials entering into the container are transported by the pressure-driven flow and move towards the membrane surface.Under the effect of the membrane filtration, the volumetric fraction of the granular materials in the container continues to increase.At a low stirring speed (60 rpm),we can find in Fig.6(a) that, the granular materials have a non-uniform distribution on the vertical plane at the initial flow stage (20 s).As the circulation loops and the vortex could increase the homogeneity of the pollutant distribution, the granular materials expand both radially and vertically with the time, and the granular materials in the container distribute more and more symmetrically.At high stirring speeds (150 rpm,250 rpm), the distribution of the granular materials on the vertical plane is almost symmetric even at the initial flow stage (20 s).It implies that the stirring speed not only increases the flow velocity, but also accelerates the mixing process in the container.Although the granular materials could expand both axially and vertically, it is of interest to notice that, the region of high concentration of the granular materials is always close to the shaft mainly as a result of the flow characteristics, as discussed in Section 2.1, that the low flow velocity in the near-shaft region allows the granular materials to stay for a long time.

Fig.7 (Color online) Evolutions of membrane fouling at different stirring speeds

Figure 7 shows the evolution of the membrane fouling at various stirring speeds.At the initial flow stage (20 s), the volumetric fraction of the granular materials on the membrane surface is small, but it increases remarkably with the time.Our numerical results can successfully explain in a qualitative way that, the evolution of the membrane fouling is accompanied and promoted by the adhesion of the granular materials on the membrane surface.The volumetric fraction of the granular materials is found to be relatively low at the membrane center, which could imply that the central area of the membrane plays a negligible role in the membrane separation process.According to the comparative analysis in Figs.7(a)-7(c), we can find that an accelerated stirring speed can significantly decrease the volumetric fraction of the granular materials on the membrane surface.This result theoretically confirms the experimental fact that the utilization of high stirring speeds is a practical strategy to avoid or to control the membrane fouling effect.

The time evolution of the average volumetric fraction of the granular materials on the membrane surface is shown in Fig.8.The granular materials are found to deposit constantly on the membrane surface with the time, which can be the factor that leads to the formation and the development of the membrane fouling.At the initial stage (＜20s), the average volumetric fraction of the granular materials increases more aggressively at a higher stirred speed.This is because a higher stirring speed could accelerate the transportation of the granular materials from the inlet to the outlet (the membrane).However, when the initial stage is over (＞20s), the increase of the stirring speed can significantly decrease the temporal deposition of the granular materials on the membrane surface.

Fig.8 Time evolutions of average volumetric fraction of granular materials on the membrane surface

3.Conclusions

This paper presents a numerical study of the flow characteristics and the membrane fouling process in a widely used enzymatic membrane reactor.A threedimensional Euler-Euler model, supplemented by thek-εmixture turbulence model and a classical drag function, is built to describe the turbulent granular flow.Our numerical model is validated by comparisons with experimental results.

In the numerical simulations, it is demonstrated that the characteristics of the single-phase flow can be significantly modified by the stirring speed.The increase of the stirring speed not only enlarges the circulation loops but also induces the significant growth of the rotational velocity, the shear stress and the turbulent kinetic energy in the reactor.By the study of the two-phase flow, we find that the mixing process of the granular materials is accelerated by the increase of the stirring speed.Furthermore, the membrane fouling mechanism can be explained in a qualitative way by the time evolution of the volumetric function of the granular materials on the membrane surface.As these numerical predictions agree well with the experimental observations, we could conclude that to a certain extent our numerical model is appropriate for the simulations of the membrane fouling effect.However, further studies are still needed for the reactors of more complex geometry.

Acknowledgments

This work was supported by the self-determined project of State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body (Grant No.51475002), the Fundamental Research Funds for the Central Universities (Hunan University).