基于极限思想对导数与定积分概念的认识与思考

张子悦

摘 要：通过对高中数学所学导数和定积分的概念以及它们的实质进行对比分析，发现尽管两者在定义上不同，但是本质上两者都是基于极限的思想，两者都属于极限问题。这一认知不仅有助于理解和掌握导数及定积分的概念、清楚它们的几何意义，还将有助于通过建立概念之间的联系，深化对导数和定积分知识的理解，提高分析和解决相关导数和定积分问题的能力，最后给出了一个应用极限解决定积分问题的算例。

关键词：导数 定积分极限 几何意义

中图分类号：G63 文献标识码：A 文章编号：1672-3791（2018）05（a）-0165-03

微积分是数学的一个基础学科[1]，它的应用涉及到多个方面，对数学、物理、工程和经济等多个领域起到了极大的促进作用。在高中数学学习过程中，首次接触到了导数和定积分，它们是整个高中阶段数学课程的重点和难点之一。通过对导数和定积分概念的学习，发现它们之间不仅有区别还存在一定的联系。下面将通过对两个概念的对比分析，深入认识它们本质上的异同。

1 导数的概念及几何意义

在微积分中，导数是其重要的概念之一[2]，它可以用来解决许多领域的实际问题，如物理中的求解速度和加速度、数学中判定函数的单调性、几何学中确定切点斜率等。

通过（1）式可知，导数从实质上来讲就是当Δx无限逼近0时，函数的变化量与相应自变量变化量比值的极限。因此，如果这个极限存在了，那么导数也就意义或者说也就存在了，反之导数不存在[2]，所以求导数追根究底就是求极限。

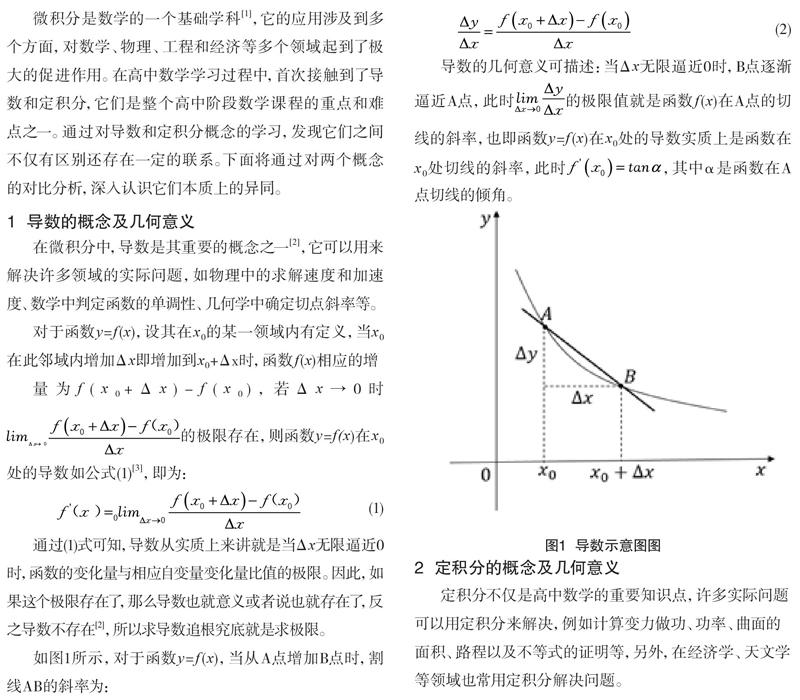
如图1所示，对于函数y=f（x），当从A点增加B点时，割线AB的斜率为：

导数的几何意义可描述：当Δx无限逼近0时，B点逐渐逼近A点，此时的极限值就是函数f（x）在A点的切

线的斜率，也即函数y=f（x）在x0处的导数实质上是函数在x0处切线的斜率，此时，其中α是函数在A点切线的倾角。

2 定积分的概念及几何意义

定积分不仅是高中数学的重要知识点，许多实际问题可以用定积分来解决，例如計算变力做功、功率、曲面的面积、路程以及不等式的证明等，另外，在经济学、天文学等领域也常用定积分解决问题。

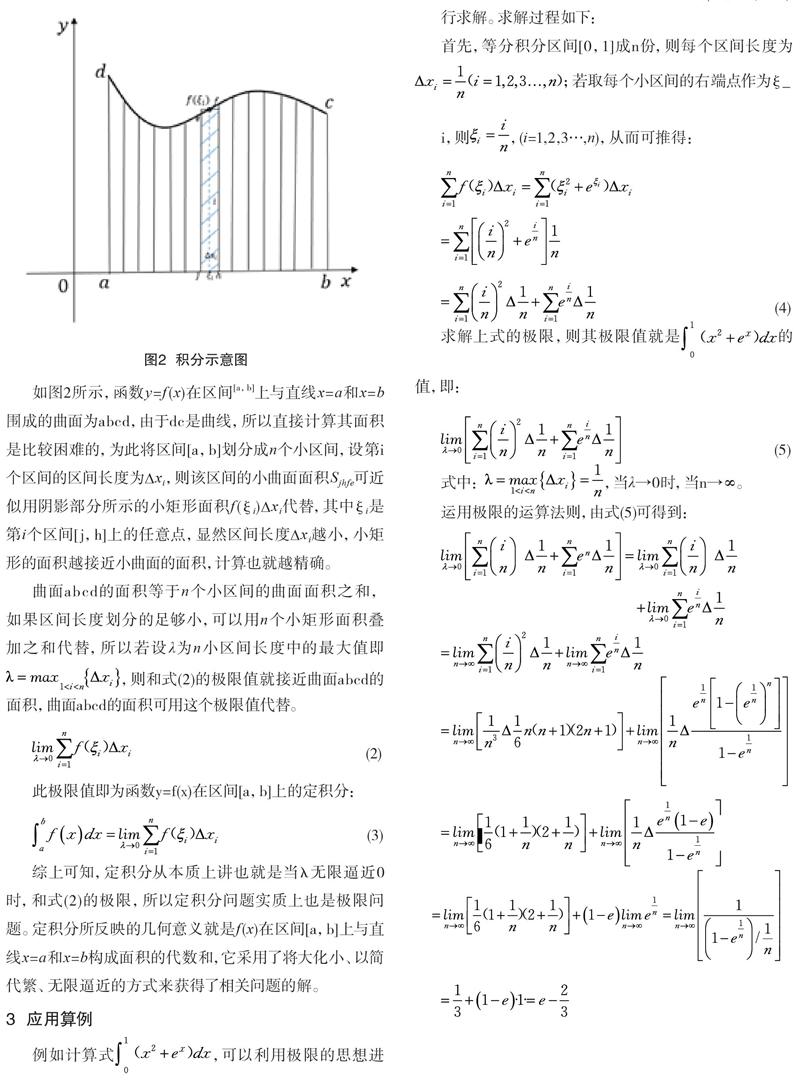
如图2所示，函数y=f（x）在区间[a，b]上与直线x=a和x=b围成的曲面为abcd，由于dc是曲线，所以直接计算其面积是比较困难的，为此将区间[a，b]划分成n个小区间，设第i个区间的区间长度为?xi，则该区间的小曲面面积Sjhfe可近似用阴影部分所示的小矩形面积f（ξi）?xi代替，其中ξi是第i个区间[j，h]上的任意点，显然区间长度?xi越小，小矩形的面积越接近小曲面的面积，计算也就越精确。

曲面abcd的面积等于n个小区间的曲面面积之和，如果区间长度划分的足够小，可以用n个小矩形面积叠加之和代替，所以若设λ为n小区间长度中的最大值即，则和式（2）的极限值就接近曲面abcd的面积，曲面abcd的面积可用这个极限值代替。

综上可知，定积分从本质上讲也就是当λ无限逼近0时，和式（2）的极限，所以定积分问题实质上也是极限问题。定积分所反映的几何意义就是f（x）在区间[a，b]上与直线x=a和x=b构成面积的代数和，它采用了将大化小、以简代繁、无限逼近的方式来获得了相关问题的解。

3 应用算例

综上，该算例就是在深入理解定积分属于极限问题的基础上，反复利用极限的运算法则获得了定积分的值。尽管这个例题比较简单，但是它给出了一种解决定积分问题的思路，特别是对于一些比较复杂的定积分问题，可以转化成极限问题，通过极限的相关运算法则、定理等来获得它们的解。

4 结语

根据前面对导数和定积分两个概念的分析可以看出，尽管导数和定积分看起来是两个不相关的数学概念，但是从极限思想的角度[4-6]，两者实质上都属于极限问题，从而两者具有了相关性。了解了这一点，不仅能够更准确的把握这两个概念，还可以将极限的相关运算法则应用到解决导数或定积分问题中，从而提高了学生解决和分析导数或定积分等相关数学问题的能力。

参考文献

[1] https：//baike.so.com/doc/3201826-3374351.html.

[2] https：//baike.so.com/doc/5386034-5622483.html.

[3] 同济大学数学教研室.高等数学[M].北京：高等教育出版社，1990.

[4] 张海燕.高等数学教学中关于极限思想的教学及其感悟[J].教育现代化，2017（14）：157-159.

[5] 张海燕，赵翠萍，徐利艳，等.微积分[M].北京：清华大学出版社，2015.

[6] 施红英.对微积分“极限”思想方法教学的思考[J].甘肃广播电视大学学报，2005（3）：70-72.