电影评分的自编码网络预测研究

黄幸颖,梁 路,滕少华

(广东工业大学 计算机学院,广州 510006)

1 引 言

在推荐系统中,用户对项目的评分通常用二维矩阵来表示,但用户已评分的项目数量有限,且随着用户数和项目数的增加,评分矩阵的规模将变大,这就是稀疏性[1]的问题.在推荐系统中被广泛采用的协同过滤算法是根据用户的历史评分数据进行推荐的,易受到稀疏性的影响,如何降低其影响成为实现协同过滤要考虑的关键问题之一[2].

有鉴于此,国内外学者从降低矩阵稀疏度这一思路出发,采用了多种方法来对空缺值进行预测,例如基于内容的方法,基于聚类的方法等.这些方法有的利用项目或用户的评分信息[3],有的利用用户或项目的文本特征信息[4],对空缺的评分进行预测.优点是简单、直观和易于解释,但存在特征的提取问题.填充时若使用项目的特征,大多情况下都只能选择文本类信息,而对于音频、视频等非文本类的项目,可供使用的文本类特征有限,限制了预测准确度的提升;若使用的是用户特征,用户出于对自身隐私的保护,普遍对显式特征收集表现出抗拒的情绪,而隐式特征收集又会涉及复杂的用户行为分析与建模,所得特征既不易于解释,也难以保证准确性.

本文采用一种基于自编码网络的模型,仅利用现有的评分信息,通过调整网络节点之间的连接状态来缓解稀疏性的影响,实现对评分矩阵空缺值的预测.实验结果表明此方法的预测准确度超过了部分常用的推荐算法.本文第二部分为协同过滤领域的评分预测方法及其特点介绍;第三部分描述自编码网络在电影评分预测中的应用;第四部分展示实验结果及分析;第五部分总结并提出下一步工作.

2 相关工作

稀疏性问题使得推荐算法产生推荐序列时要分两步:第一,按照一定的标准预测评分矩阵当中的空缺值;第二,在第一步的基础上进行Top-N推荐[5].解决稀疏性问题的常用方法有固定值、基于人口统计属性、基于内容、基于社交网络等.以上方法能在一定程度上缓解稀疏性对推荐所带来的影响,但有的没有考虑用户之间或项目之间的评分差异,难以保证预测结果的个性化;有的需要用户或项目的额外信息,需要另外获取[6-9].

Salakhutdinov和Hinton将深度学习和协同过滤进行结合,通过在Netflix数据集上使用受限波尔兹曼机(Restricted Boltzmann Machine,简称RBM)为用户建模,对未知的电影评分进行预测,取得了不错的效果[10].该方法尝试为每一个用户建立一个模型,但用于模型训练的样本只有一个,即用户自身的历史评分记录,而其他用户的评分信息却未能得到充分利用.

作为深度学习的基础模块之一,自编码网络是一个三层的神经网络,输入层到隐含层为编码层,隐含层到输出层为解码层,整体来说,自编码网络是在学习输入数据的某种表示[11].由若干个自编码网络组成的堆栈式自编码网络(Stacked Auto-encoder,简称SAE)已被用于分类问题的求解[12].

自编码网络及其变型也常被用于输入数据的特征提取.Xie[13]将这一结构应用到图像的识别与去噪中,结果表明自编码网络提取出来的特征能提高识别准确率.Vincent[14]用去噪自编码网络来提取音乐特征,取得了很好的效果.胡振[15]用去噪自编码网络组成混合模型解决作曲家分类问题,实验结果表明自编码网络在特征提取上存在优势.江国荐[16]将堆叠自编码网络用于网页分类,由于文本特征表示的特征向量维度高,而网页文本属于短文本,显然用于文本特征表示的特征向量是一个稀疏向量,这与电影评分数据中各个用户的评分向量是稀疏的一致.此外,该文实验采用堆叠自编码网络进行特征选取,结果证明自编码网络可以更贴切地表达文本特征.综上所述,故本文采用自编码网络来提取用户评分中的隐含特征.

3 电影评分的自编码网络

3.1 场景预设

假设现有一个用户-项目评分矩阵如表1所示,共有4名用户和5部电影.评分值为1到5之间的整数,分值越大,表示用户的喜好程度越高.现在要预测表中的空缺值,即用户张三对电影《黄金时代》,用户李四对电影《十七岁》等的评分.

表1 用户-项目评分矩阵
Table 1 Users-items rating matrix

黄金时代亲爱的十七岁大话西游岁月神偷张三132李四154王五233赵六513

基于用户的协同过滤方法首先会计算用户之间的相似度,然后用相似用户对目标项的评分来填充相应的空缺值.例如,用户张三和赵六的相似度最高,因此用户张三对电影《黄金时代》的评分就用赵六对《黄金时代》的评分5分来填充.此方法优点是简单直观,但在预测空缺值时仅考虑目标项的评分,忽略了各个项目评分之间可能存在的联系.而自编码网络能从用户的评分中提取特征,有利于发现项目评分之间的相关性,提高准确度.

3.2 自编码网络建模

在电影评分的预测中,假设有N个用户,M部电影,相关的定义如下:

定义1.用户ui对电影mj的评分

定义2.用户ui对所有电影的评分

定义3.输入层第j个节点激活标志flagj

当自编码网络的输入数据中隐含着一些特定结构,比如某些输入特征是彼此相关的,那么自编码网络可以发现输入数据中的这些相关性,进而对输入数据进行有效的表示.

图1 电影评分预测的自编码网络结构Fig.1 Auto-encoder structure in film rating predicts

本文所构建的自编码网络是一个三层神经网络,其网络结构如图1所示.其中输入层节点个数等于电影数M,与隐层节点的连接状态用虚线表示,当该节点的激活标志为1时建立与隐层节点的连接,否则不建立连接.输出层为一个softmax分类器,对应5个输出节点,分别代表1到5分.

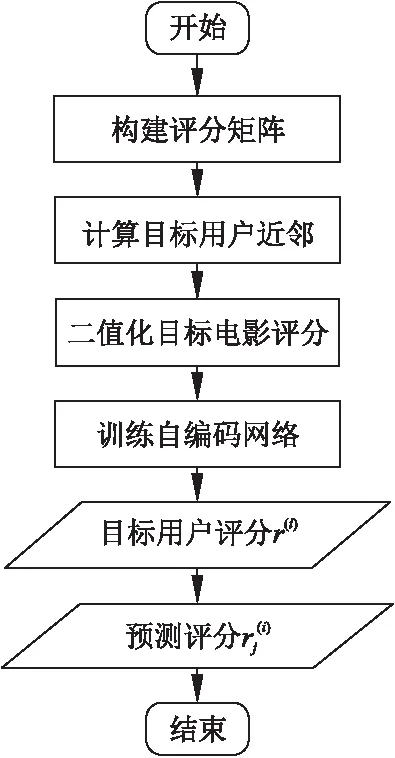
图2 电影评分预测流程Fig.2 Film rating predicts process

然而在实际应用场景当中,用户ui已给出评分的电影数目占总电影数目的比例很小,因此r(i)中有很多空缺值.将用户的评分输入到模型的时候,不能简单地将空缺的评分值用0来代替,此举会严重降低预测的准确度.因为自编码网络能够学习输入数据的特征表示,大量地输入0会让网络学习到用户评分的负偏好,错误地认为这个用户的评分十分严谨,甚至是苛刻,致使预测阶段得到的评分偏低,这显然不符合实际情况.有鉴于此,在本文所构建的模型中增设输入节点的激活标志,当该节点的激活标志为1时才将其值作为网络的输入.因为输入的都是确实存在的评分,这些评分组成了概念上稠密评分记录,每次激活值的计算及权重的调整都只发生在实际建立连接的节点上,使得模型能在一定程度上缓解稀疏性带来的影响.与此同时,由于自编码网络在训练阶段学习的是一个输出等于输入的函数,即hW,b(r(i))≈r(i)此举保证了自编码网络提取出来的隐层特征能够很好地还原出输入数据,从鲁棒性角度而言,这些特征较一般的神经网络提取出来的特征更优,故自编码网络能够发现用户评分中的隐含特征.

3.3 预测流程

现在要预测用户张三对电影《黄金时代》的评分,整个预测流程参照图2.

首先求出张三的近邻.以表1的数据为例,各用户之间的皮尔逊相似度(Pearson Correlation Coefficient)如表2所示.根据用户之间的相似度选取出近邻,则张三的近邻为王五和赵六.

表2 用户的皮尔逊相似度
Table 2 Pearson similarity of users

张三李四王五赵六张三1.0-0.930.950.71李四-0.931.0-1.0-0.99王五0.95-1.01.00.90赵六0.71-0.990.901.0

由于网络的输出层是一个分类器,故需要获得训练样本的类标签.现将王五和赵六对《黄金时代》的评分进行抽取,二值化后作为训练样本的类标签.{1,0,0,0,0}表示评分值为1分,{0,1,0,0,0}表示评分值为2分,如此类推.但王五对《黄金时代》的评分空缺,故王五的评分数据被抛弃不用.

利用近邻的评分信息,通过逐层训练,全局微调的方式即可获得一个用于预测的自编码网络.其中,全局微调阶段的整体损失函数为:

W代表整个网络的权值,b代表偏置(bias).对应上述例子,n等于1,i等于2,j等于1.上式中,第一项是重构误差项,第二项是正则项,用来防止网络出现过拟合.由于自编码网络的优化问题是一个非凸优化问题,采用反向传播求解损失函数最小值的过程中可能会陷入局部极小值.为了避免这一情况的发生,可以在权重调整时采用动量调整的方式来降低陷入局部极小值的概率.

将用户张三对所有电影的评分r(1)输入到训练好的网络中.经过一次前向传播即可得到输出层节点的激活值.选择激活值最大的节点所对应的评分作为张三对电影《黄金时代》的预测评分.

4 实验分析

4.1 实验数据集

实验选用MovieLens1数据集:第一个是MovieLens 100k,该数据集包含了943位用户在1682部电影上的100,000条评分记录,稀疏度约为93.7%;第二个是MovieLens 1m,该数据集包含了6040位用户在3952部电影上的1,000,209条评分记录,稀疏度约为95.8%.两个数据集的评分都是1到5之间的整数,分布情况如表3所示,可见在两个数据集中,3分及以上的评分均占总评分数的80%以上,4分及以上的评分占总评分数的50%以上,评分分布明显不平衡.

表3 数据集评分分布
Table 3 Distribution of rating datasets

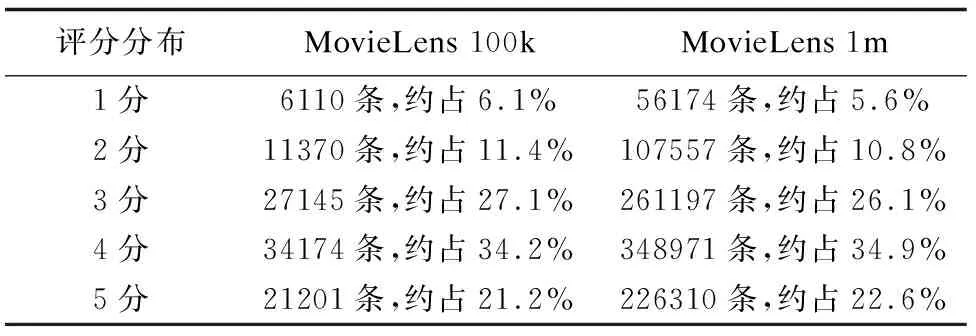
评分分布MovieLens 100kMovieLens 1m1分6110条,约占6.1%56174条,约占5.6%2分11370条,约占11.4%107557条,约占10.8%3分27145条,约占27.1%261197条,约占26.1%4分34174条,约占34.2%348971条,约占34.9%5分21201条,约占21.2%226310条,约占22.6%

数据集中的数据随机选取80%的评分数据作为训练样本,剩下的20%作为测试样本.

4.2 准确度评估标准

准确度指标采用平均绝对误差(Mean Absolute Error,简称MAE),和均方根误差(Root Mean Squared Error,简称RMSE)来衡量.

平均绝对误差的计算公式如下:

均方根误差的计算公式如下:

4.3 结果分析

表4展示了自编码网络与基于用户的协同过滤、基于项目的协同过滤、Slope One、SVD这4种常用的推荐算法和BP神经网络.在两个数据集上的对比结果.

在100k这个数据集上,自编码网络的MAE值为0.776,优于BP神经网络的0.802和SVD的0.781,仅次于Slope One的0.747,而在RMSE值上,自编码网络的0.983要逊于Slope One的0.947,优于基于用户的协同过滤的1.275和BP神经网络的1.051.而在1M数据集上,自编码网络获得的结果与100k上的相似,MAE值优于BP神经网络和SVD,仅次于Slope One;RMSE值则位居第二,依然次于Slope One.

从实验结果中不难看出以下几点:

1)针对电影评分数据稀疏、冗余和不平衡的特点,本方法同时考虑了近邻之间的评分相似性和项目之间的评分相关性.从预测准确度来看,得益于自编码网络的特征提取优势,自编码网络隐层提取的特征要优于BP神经网络提取的特征.

2)自编码网络在大数据集上的准确度要高于小数据集上的准确度.因为较大的数据集能够提供更多的训练样本,强化了近邻之间的评分相似性和项目之间的评分相关性,有助于提取评分信息的更一般特征,提高网络的泛化性能.

表4 各种推荐算法的准确度
Table 4 Accuracy of recommendation algorithms

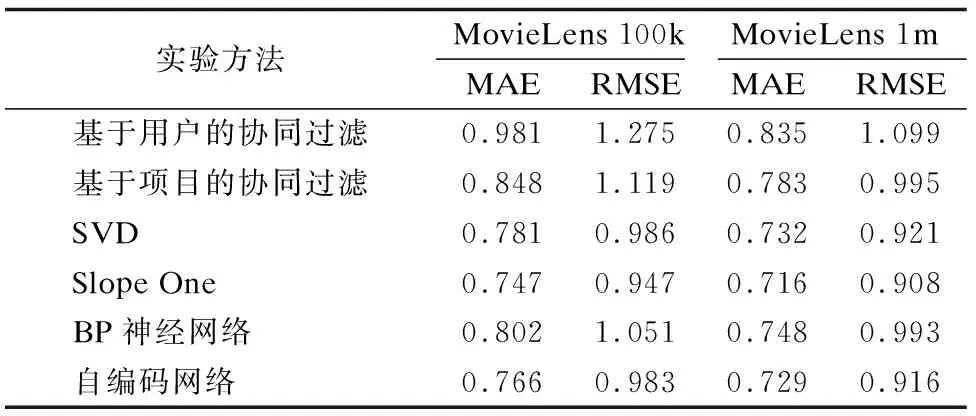
实验方法MovieLens 100kMovieLens 1mMAERMSEMAERMSE基于用户的协同过滤0.9811.2750.8351.099基于项目的协同过滤0.8481.1190.7830.995SVD0.7810.9860.7320.921Slope One0.7470.9470.7160.908BP神经网络0.8021.0510.7480.993自编码网络0.7660.9830.7290.916

3)自编码网络上的MAE值和RMSE值相差约为0.2,大于基Slope One上的差值.因为训练自编码网络涉及非凸函数的优化求解,存在局部极小值,使得预测结果不够稳定,波动较大.

5 结 论

本文利用自编码网络将评分预测问题转换为多分类问题来解决,通过设置节点激活标志来调整输入节点与隐层节点连接状态,能在一定程度上降低稀疏性对预测准确度的影响.所得隐含特征在实现评分信息近似表示的同时,提高了预测准确度,为处理评分冗余且分布不平衡的稀疏矩阵形成支撑,在协同过滤稀疏性问题的背景下有一定的应用价值.实验表明,本方法能获得比部分常用的协同过滤算法更高的预测准确度,具有较好的可扩展性,但在训练网络时需要较多的计算资源,对冷启动问题的解决也有待加强.