EM算法的ε-加速及在有限混合模型中的应用

鲁纳纳，余旌胡，丁立新，林广明

（1. 武汉理工大学，湖北 武汉 430072；2. 武汉大学 计算机学院, 湖北 武汉 430070；3. 深圳信息职业技术学院 信息技术研究所，广东 深圳 518172）

引言

EM算法是处理非完整数据未知参数的一种迭代方法，由Dempster[1]等人提出，用来估计出非完整数据条件下(包括隐含数据和缺失数据等)的模型参数值，广泛应用于截尾数据、删失数据、成群数据等，每次迭代由E步(期望步)和M步(极大步)组成。E步是计算不完整数据的条件期望来填充不完整数据，M步是在E步的基础上求解未知参数的极大似然估计。

自Dempster等人提出解决不完整数据参数估计的EM算法以来，国内外有许多研究者对EM算法进行了更进一步的研究。如Wu和Xu[2-3]总结出EM算法的一些收敛性质。Meng和Rubin[4]提出条件期望最大化方法（ECM）来优化M步，使得条件期望的极大化更加简洁。Liu和Rubin[5]提出了ECM方法扩展ECME方法，这种方法对ECM算法中的CM步中对数似然函数的极大化条件进行了修改，加快了EM算法和ECM算法的收敛，此外，还提出了交替ECM算法；而当期望解析表达式难以得到时，Wei和Tanner[6]提出了蒙塔卡罗EM算法，改进了EM算法中的E步，使得E步更易实现。但当未知数据较多时，收敛速度会变慢。为了提高EM算法的收敛速度，Jamshidian和Jennrich[7]提出了一种基于共轭梯度的加速算法，使用拟牛顿法加速了EM算法。因为使用牛顿法加速需要在每轮迭代中计算矩阵的逆，当参数变多时，其计算量会变得非常复杂，计算结果也会不稳定。而Kuroda等人[8]提出的用ε-加速EM算法在解决二维列联表中缺失数据时表现比较优异，能在加速EM序列收敛速度的同时，不影响其稳定性、灵活性和简单性，但是未涉及到初始值的影响以及在有限混合模型下的灵敏度分析。近几年一些研究者研究了其它加速算法[9-11]并分析了加速算法在高维混合模型中的EM算法的迭代性能。EM算法易受初始值影响，不能保证找到全局最优，往往容易陷入局部最优，因此关于初始值设置提出了许多方法，Zhai[12]选取最远点为初始值，易使边界点收敛效果受到影响；Li和Chen[13]使用k-最近邻法删除异常值，然后用K-means来初始化，此估计效果显著优于原始效果。

关于EM算法的初始值设置和收敛速度方面，研究者们已提出许多改进的方法，但对有限混合模型参数求解方法的研究方面，在保留EM算法的各种优点的同时，又能加快收敛速度的方法及其有效性分析的工作并不多。因此，本文首先运用k-means方法对原始数据进行聚类，从而选取合适的初始值；其次运用数值分析中的ε-加速算法对EM算法得到的迭代序列进行变换，进一步加快其收敛速度(K-means+ε-加速EM算法)。因高斯分布具有灵活、高效拟合的特点，并且很多随机现象在足够大样本下都可以用此分布来逼近[14]，本文设计数值实验，比较加速前后EM算法在高斯混合模型参数估计中的时间成本与精度误差。在灵敏度分析方面，分析在不同条件下加速前后EM算法的参数估计效果。

1 EM算法和有限混合模型相关原理

1.1 EM算法的基本原理与收敛性

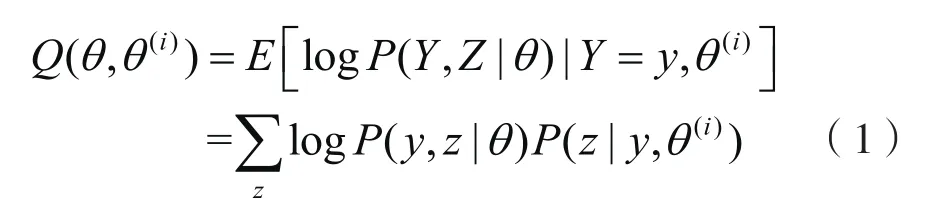
反复进行E步和M步，直至收敛。

关于EM算法的收敛性有如下结果：

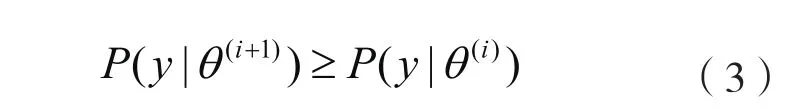
由于

两边取对数得到

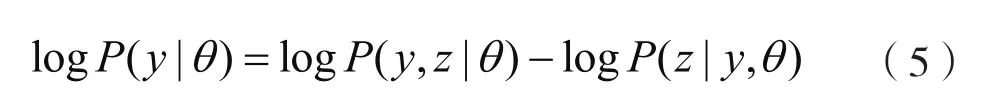
令

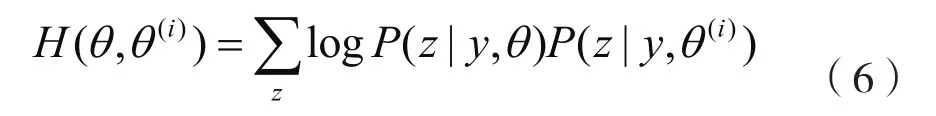
于是对数似然函数可以写成

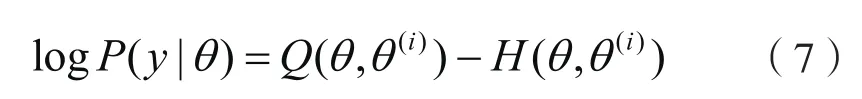
从而

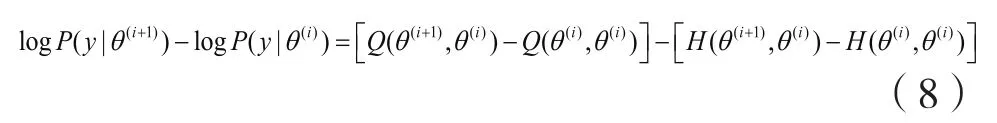
要证明

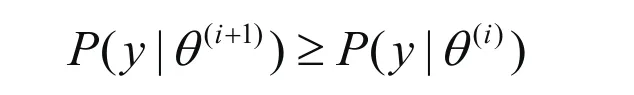
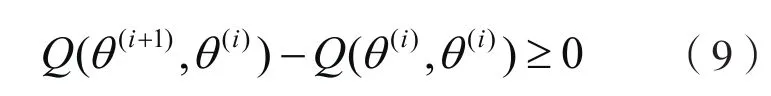
EM算法是一个一阶逐次替代方法并隐性地定义了从参数空间Θ到Θ的一个映射()Mθθ→使得

这里λ是*J的最大特征值。从上式可以看出：迭代序列其中c是一个常数，且01c＜＜。这里λ对应c，因此EM序列线性收敛。

1.2 有限混合模型

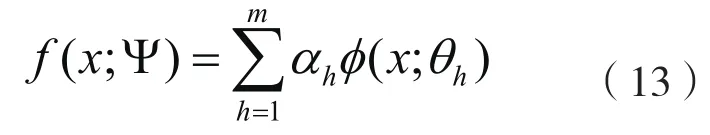
case1：两分量高斯混合模型的一般框架的推导：

（2）混合模型的形式

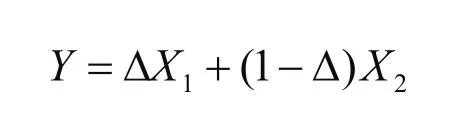
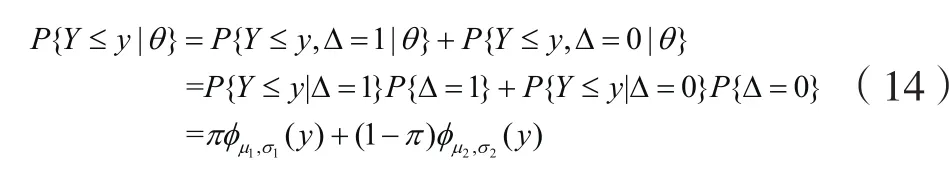
(,)Y Δ 的联合概率函数为

其中yk对应的类别为取值为0 1-。

若将（1）为目标函数，由Jensen不等式知下式成立：

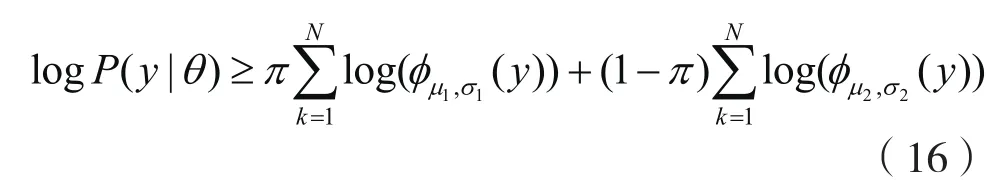
若将（15）为目标函数，由Jensen不等式知：

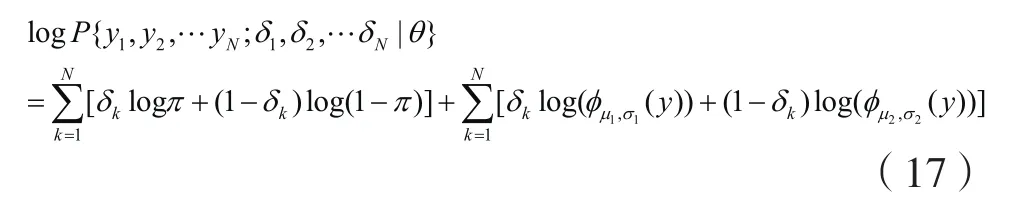
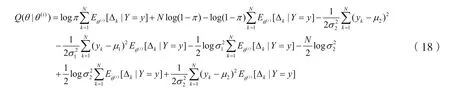
case2：用类似的方法可以求出三分量高斯混合模型的迭代公式：

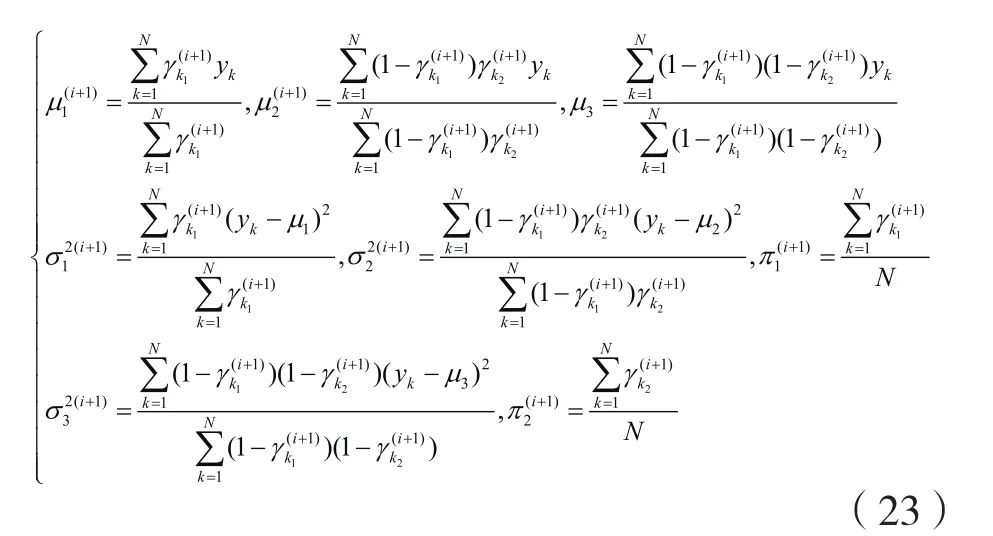
1.3 针对有限混合模型的k-means方法

EM算法对初始值十分敏感，如果初始值选取不当，不仅可能陷入局部极值，不能得到全局最优解，甚至有可能无法正常进行迭代。在EM算法初始值选取上，常用的方法是选取几个不同的初值进行迭代，然后对得到的各个结果进行比较，从中选取最优的估计值。然而这种方法是任意给定的，不仅会影响算法效率，也有可能仍然找不到全局最优解。为了提升效率，考虑在给定初始值之前进行聚类，把两种类型的数据分开，再用聚类后的中心赋值给初值。

本文采用K-means进行聚类，其相似性度量采用欧氏距离，具体步骤如下：

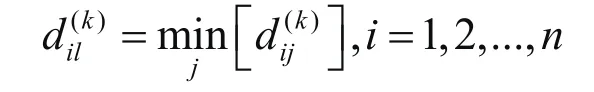
则

（3）计算重新分类之后的类心

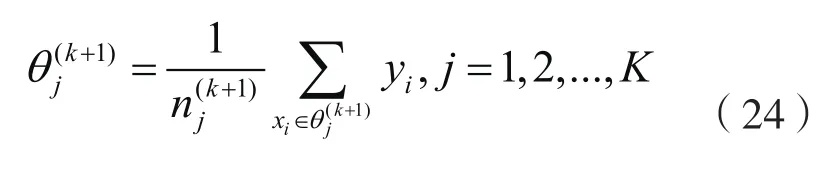
1.4 EM算法的ε-加速

（1）ε-加速方法

Wynn[16]提出ε-算法来加速收敛缓慢的序列，此算法对于线性收敛的序列非常有效。具体流程为：

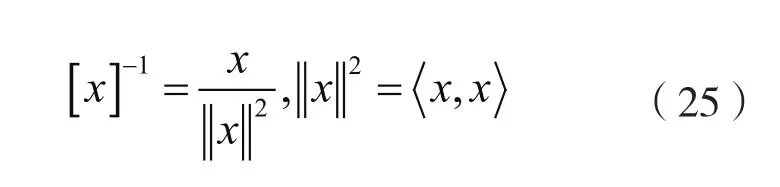
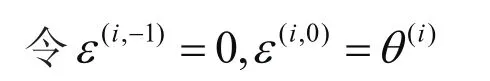
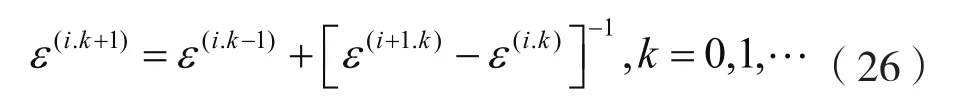
一般情况下，上式中 0r=

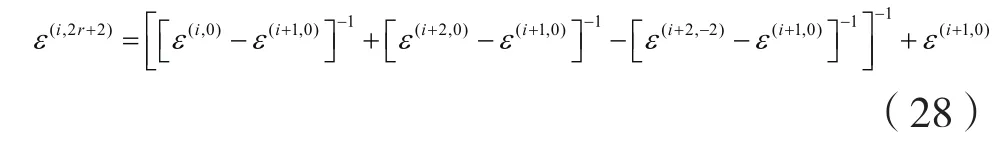
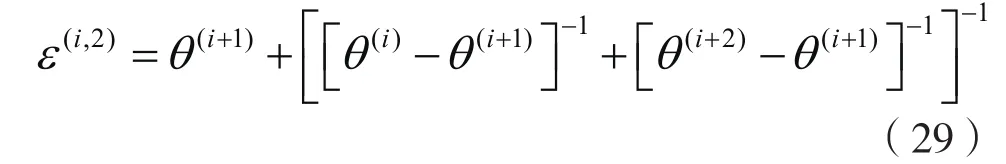
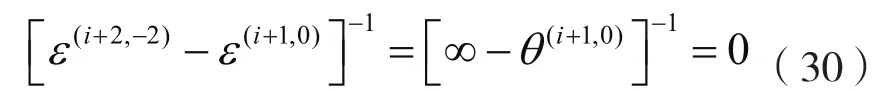
（当i趋于无穷大）。注意，在每一次迭代中，ε-加速算法只需要次运算，而Newton-Raphson算法和拟牛顿算法分别需要次运算，随着维数d变高，计算成本也会变大。

（2）EM算法的ε-加速算法

ε-加速步：计算

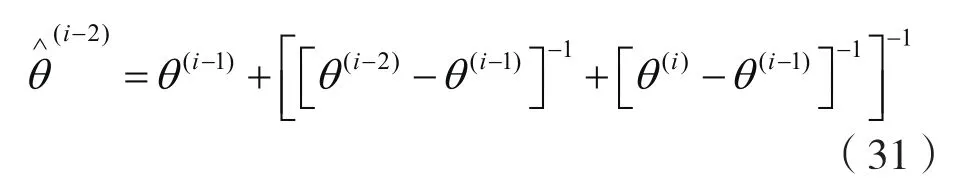
终止条件

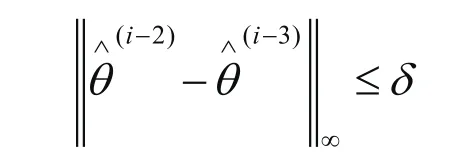
这里δ是预期精度。注意到ε-加速EM算法并没有改善E和M步，而是通过ε-加速过程加速EM序列收敛。

为了比较EM算法和ε-加速EM算法的收敛速度，引用以下概念[17]：

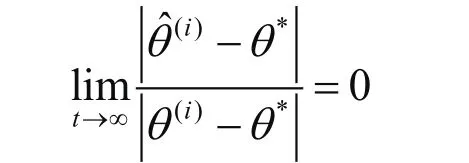
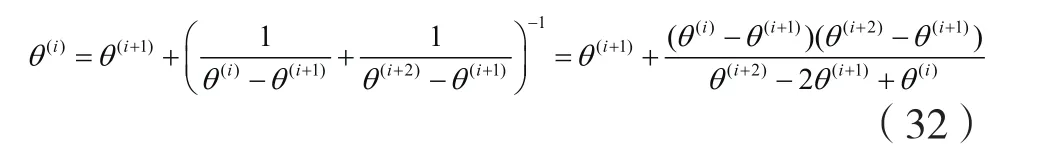
Traub[18]证明了因此，ε-EM算法加快了原始的EM序列。

ε-加速EM算法通常用不依赖统计模型的（31）式。而牛顿加速方法需要对每一个统计模型推导出加速公式。因此，ε-加速EM算法相对而言较简单。但如果初始值再引入K-means聚类的话，ε-加速EM算法和K-means+ε-加速EM算法的时间成本、误差精度以及灵敏度的未涉及，因此，本文进行更进一步的分析。

2 数值实验

本文采用两分量、三分量高斯混合模型为例，对EM算法、ε-加速EM算法以及本文提出的K-means+ε-加速EM算法对混合模型参数迭代求解效果进行分析。同一模型下，算法各运行100次，然后求其平均值，通过研究算法迭代次数c和值估计值与真实值的最低匹配位数m来进行时间成本和精度等多方面影响分析。

2.1 样本数量与模型分量大小对迭代效果的影响分析

表1 样本分量 6000,=4000Tab.1 Sample component 6000,=4000

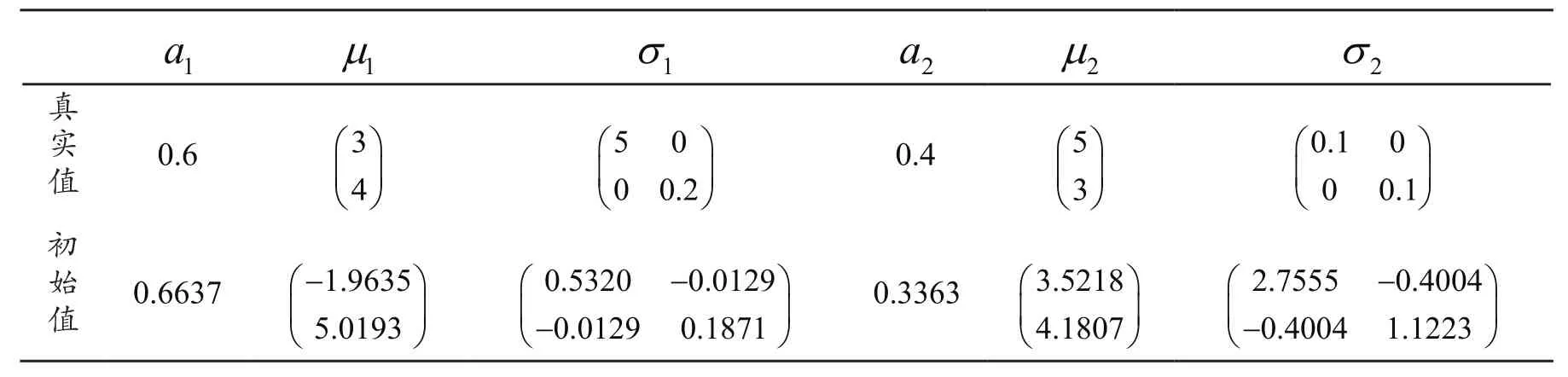
表1 样本分量 6000,=4000Tab.1 Sample component 6000,=4000

1 a 1m1σ2a2m2σ真实值 0.6 3 4■■■■■■5 0 0 0.2■ ■■ ■■ ■0.4 5 3■■■■■■0.1 0 0 0.1■ ■■ ■■ ■初始值0.6637 1.9635 5.0193-■ ■■ ■■ ■0.5320 0.0129 0.0129 0.1871-■■■■■-■0.3363 3.5218 4.1807■ ■■ ■■ ■2.7555 0.4004 0.4004 1.1223-■■■■■-■

表2 加速前后参数估计对比表Tab.2 Comparison table of parameter estimation before and after acceleration

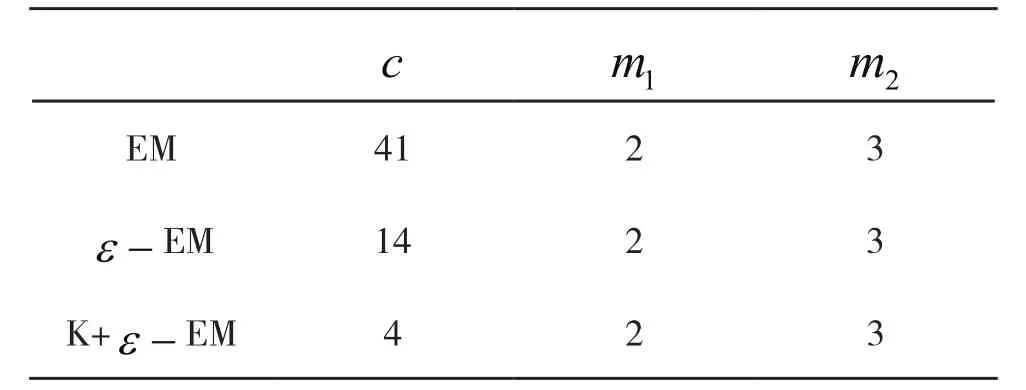
表3 迭代次数和匹配位数比对表Tab.3 Iteration number and matching digit alignment

首先从表2知，EM算法、ε-加速EM算法以及K-means+ε-加速EM算法均可以收敛到稳定点；其次从表3知，EM算法、ε-加速EM算法、K-means+ε-加速EM算法的迭代次数是递减的，并且ε-加速EM算法平均迭代次数为14次，而K-means+ε-加速EM算法仅需要ε-加速EM算法中的4个点就可以达到收敛的效果；最后从精度来分析，各种情形下的m值与真实值的匹配位数均相同，而ε-加速EM算法需要的迭代次数是K-means+ε-加速EM算法的3倍左右。

表4 样本分量600000,=400000Tab.4 Sample component 600000,=400000

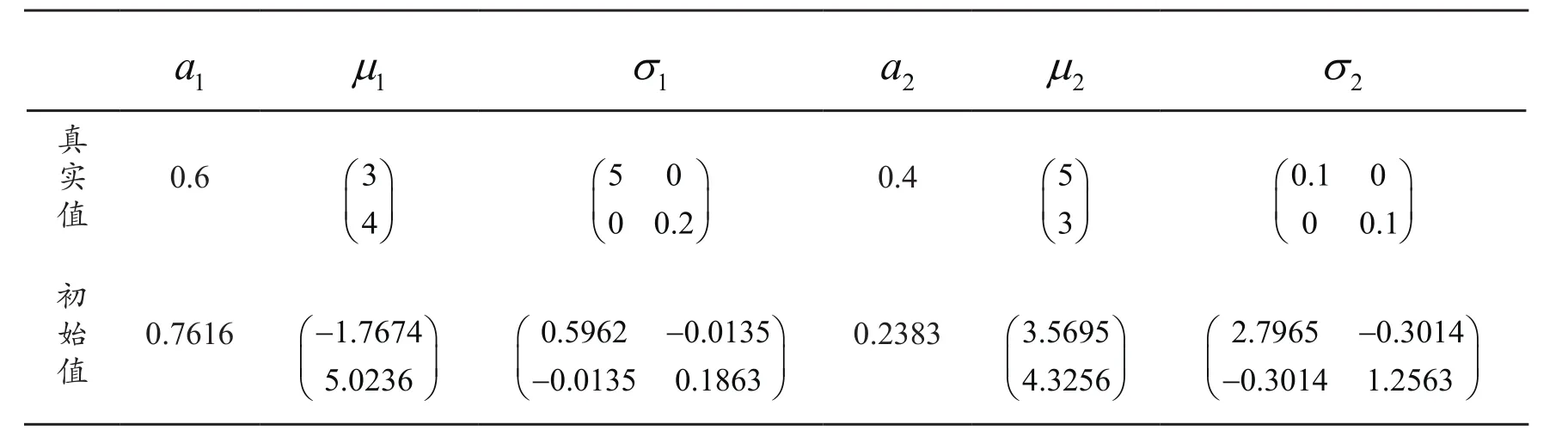
表4 样本分量600000,=400000Tab.4 Sample component 600000,=400000

1 a 1m1σ2a2m2σ真实值0.6 3 4■■■■■■5 0 0 0.2■ ■■ ■■ ■0.4 5 3■■■■■■0.1 0 0 0.1■ ■■ ■■ ■初始值0.7616 1.7674 5.0236-■ ■■ ■■ ■0.5962 0.0135 0.0135 0.1863-■■■■■-■0.2383 3.5695 4.3256■ ■■ ■■ ■2.7965 0.3014 0.3014 1.2563-■■■■■-■

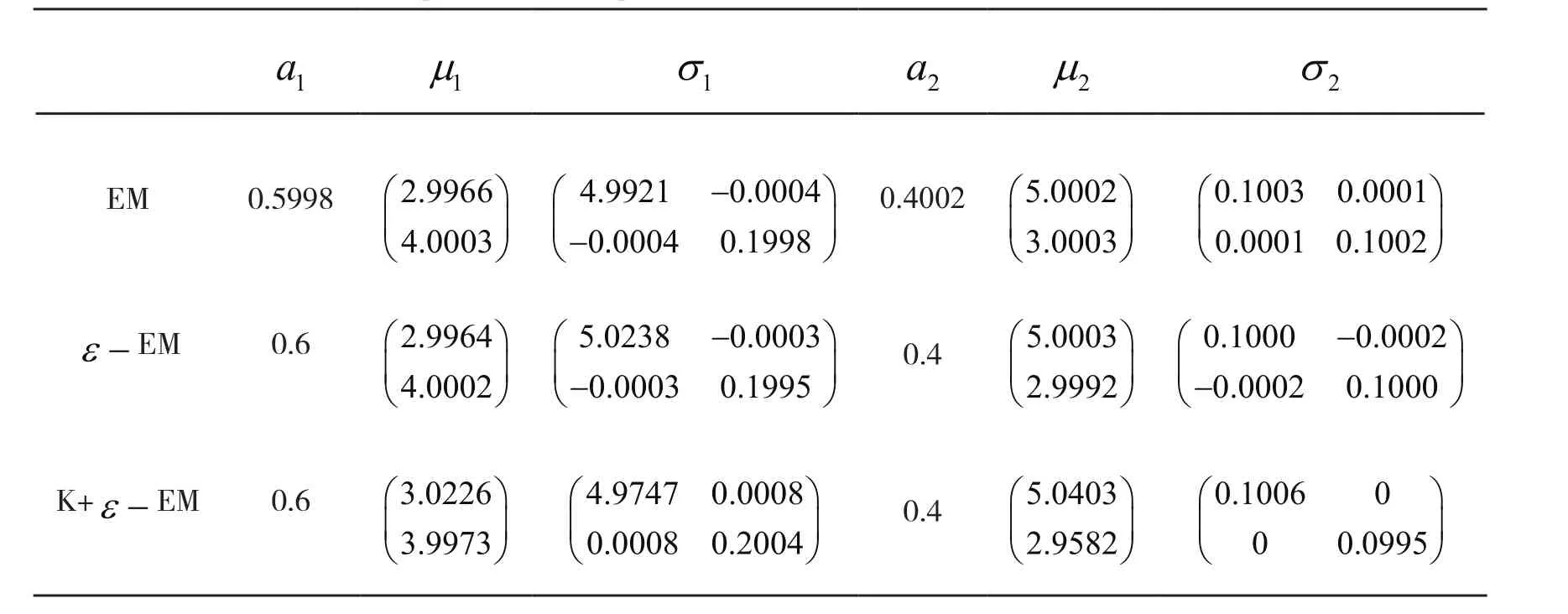
表5 加速前后参数估计对比表Tab.5 Comparison table of parameter estimation before and after acceleration

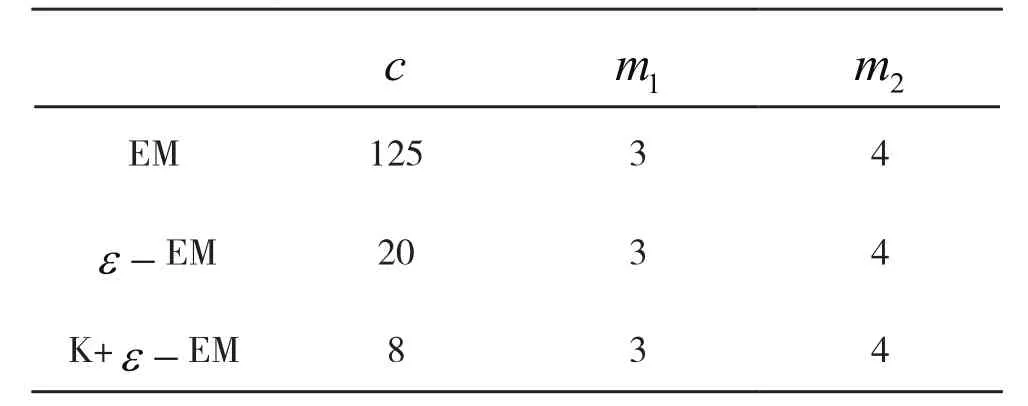
表6 迭代次数和匹配位数比对表Tab. 6 Iteration number and matching digit alignment

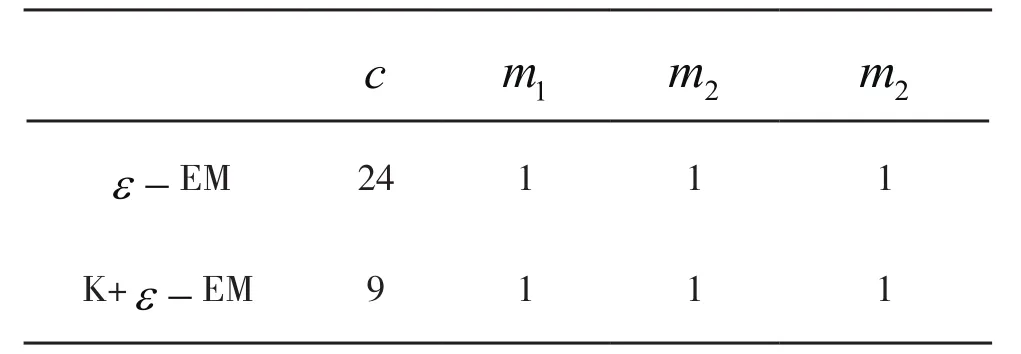
表7 三分量高斯混合模型迭代次数对比表Tab.7 Three-component Gaussian mixture model iteration number comparison

将两分量增加到三分量之后，ε-加速EM算法以及K-means+ε-加速EM算法仍可以收敛到稳定点，但二者平均迭代次数都有明显增加，精度也是均有下降。在这种情况下，ε-加速EM算法平均迭代次数从14次增加到24次， K-means+ε-加速EM算法的平均迭代次数从5次增加到9次。正如我们前面介绍的，当模型未知变量比例较高时，EM算法的收敛速度会明显变慢。同时两分量增加到三分量后，本文提出的K-means+ε-加速EM算法的效果仍然十分明显。

2.2 精度设置对迭代效果的影响分析

表8 加速前后参数估计对比表Tab.8 Comparison table of parameter estimation before and after acceleration

表9 迭代次数对比表Tab.9 Iteration number comparison table

从表9可知，随着精度增加，ε-加速EM算法和K-means+ε-加速EM算法的估计值仍然比较接近真实值，但是ε-加速EM算法估计值的匹配位数却要比K-means+ε-加速EM算法估计值匹配位数差了1位。从迭代次数来看，EM算法的平均迭代次数从14次增加到了17次；而ε-加速EM算法的平均迭代次数却稳定在4次左右。精度提升后，EM算法的平均迭代次数有明显增加，而ε-加速EM算法的平均迭代次数仍然变化不大。这说明了随着收敛精度增加，ε-加速EM算法加速效果越明显，且迭代结果更加精确。

2.3 初始值的灵敏度分析

表10 三种方法的迭代效果Tab.10 Iterative effect of three methods

由表10可知，通过K-means算法和EM算法迭代得到的估计值与真实值有较大差别，即它们的聚类效果受到了类间重叠的影响。而K+EM算法的迭代效果与真实值比较接近，说明本文用K-means方法聚类是可行的。

3 总结

评价一个算法的优越性通常有简单性、计算速度、迭代效率。对于EM算法这类迭代算法，其迭代效率备受关注，而影响迭代效率的主要因素是初始值的设置和收敛速度。本文针对EM算法初始值设置和收敛速度两个方面进行分析，通过使用K-means聚类方法进行初始值的选取，并运用ε-加速EM算法进行加速(即K-means+ε-加速EM算法)。研究了ε-加速EM算法和K-means+ε-加速EM算法在有限混合分布模型中的应用，将为混合模型参数迭代算法提供改进思路并进行有效扩充，数值实验表明，在改变观测数据量大小，收敛精度大小和分模型个数的情况下，K-means+ε-加速EM算法均比ε-加速EM算法达到更好的收敛效果，此外，从迭代次数和灵敏度两方面，验证了K-means+ε-加速EM算法是可行的。