2018年高考数学文化试题的评析与教学建议

李汝雁 郭要红

(安徽师范大学数学与统计学院 241000)

数学是人类文化的重要组成部分.数学文化指数学思想、精神、方法、观点，以及它们的形成和发展，其主要涉及数学史、数学美、数学教育、数学与人文的交叉、数学与各种文化的关系等.[1]《2017年普通高考考试大纲修订内容》中关于数学学科明确提出了“增加数学文化”的要求.[2]《普通高中数学课程标准(2017年版)》把“注重数学文化的渗透”和“断引导学生感悟数学的科学价值、应用价值、文化价值和审关价值”作为高中数学课程基本理念之一.[3]彰显数学文化的命题在高考中也就尤为必要.对2018年高考数学文化试题进行剖析，一方面为后续高考命题者命制出素材更加丰富和题型更加新颖的试题提供启发.另一方面，为广大中学数学教师更合理地利用教材进行数学文化的教学提供可借鉴的方法.

1 数学文化试题评析

据统计，2018年的13套高考试卷中有8套试卷出现数学文化试题共6道，为了更直接地体会高考试卷中的数学文化试题，列表如下(表1)：

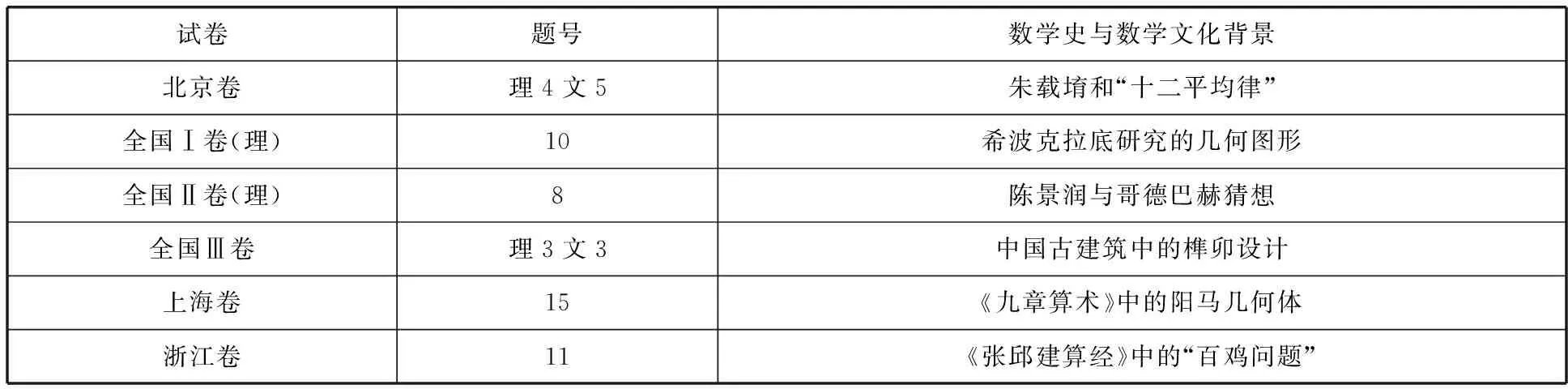
表1 2018年高考试卷中数学文化试题

从上述统计结果可以看出2018年的数学文化试题存在如下特征：第一，从题型来看，均为选择题和填空题，未涉及到计算题与证明题；第二，从知识点的分布来看，涉及数列、概率、三视图等；第三，从题目来源来看，包括以《九章算术》、《张邱建算经》等中国古代经典数学著作中的数学名题，以及国内外数学家的优秀成果、数学与其他学科的联系和实际生产生活的内容等为背景.

通过对2018年高考试卷的分析，发现其数学文化试题的命制来源有以下几种，下面分别展开论述.

1.1 以国内外数学家的优秀成果为背景

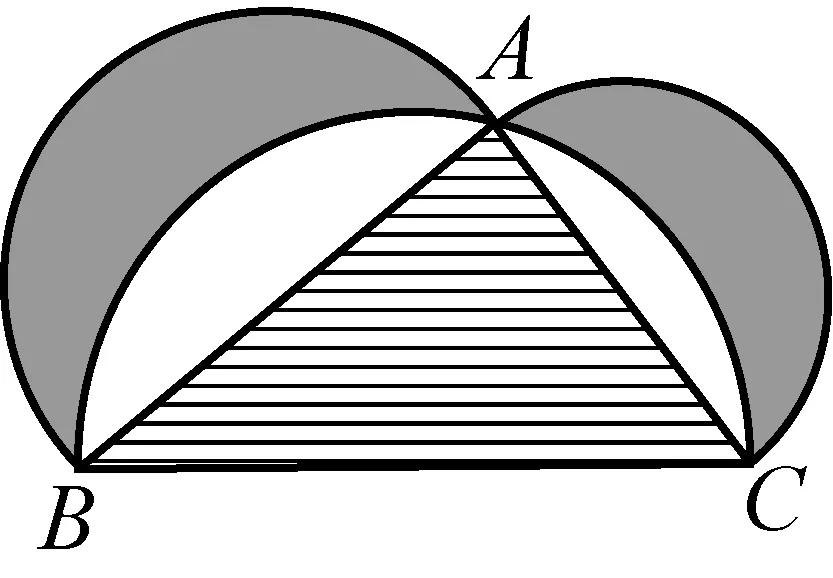
(全国Ⅰ卷(理)10)下图来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC，△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ，在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别记为p1，p2，p3，则

A．p1=p2B．p1=p3

C．p2=p3D．p1=p2+p3

评析：本题从题目条件和问题来看，一般会直接采用几何概型计算概率的方法求解，但是，作为选择题，在考场上，这样的方法显然有些复杂.这道题表面上是计算概率，实际上，如果学生清楚“希波克拉底定理”的内容，那么，问题就迎刃而解了.希波克拉底定理：“以直角三角形两条直角边向外做两个半圆，以斜边向内做半圆，则三个半圆所围成的两个月牙型面积之和等于该直角三角形的面积.”[4]根据定理内容，即可知答案为A.

(2)陈景润与哥德巴赫猜想

(全国Ⅱ卷(理)8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30=7+23．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是

评析：本题是以我国数学家陈景润在哥德巴赫猜想的研究中取得世界领先成果为背景的一道古典概率计算问题，题目难度不大，目的是使考生潜移默化地感受我国数学取得的成就.不超过30的素数有2，3，5，7，11，13，17，19，23，29共10个，随机选取两个不同的数，可能的情况有45种，其和等于30的组合有7和23，11和19，13和17，共3组，所以答案为A.

1.2 以中国经典数学史料中的数学名题为背景

(1)《九章算术》中的阳马几何体

（4）志愿者得不到理解和尊重，地位不高。这一困境是由志愿者本身及社会环境内外两个因素共同造成的。内在因素是志愿者本身存在以上三种伦理问题。外在因素是社会大众的认识及文化的影响。包括部分地方政府、相关企业单位对高校青年志愿服务活动缺乏认同和理解，把志愿服务理解为一种必须配合完成的“政治任务”，学生在服务过程中得不到真正的锻炼，导致同学们参与志愿服务的动力不足。同时，受中国传统伦理和社会结构的影响，当个体面临困难时，倾向于找到为自己负责的关系，而非求助于社会的公益事业，这种关系存在亲疏远近，对没有“关系”的人不信任，我们的青年志愿者往往被当作“陌生人”被排除在这种“关系”之外。

(上海卷 15)《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以AA1为底面矩形的一边，则这样的阳马的个数是( )

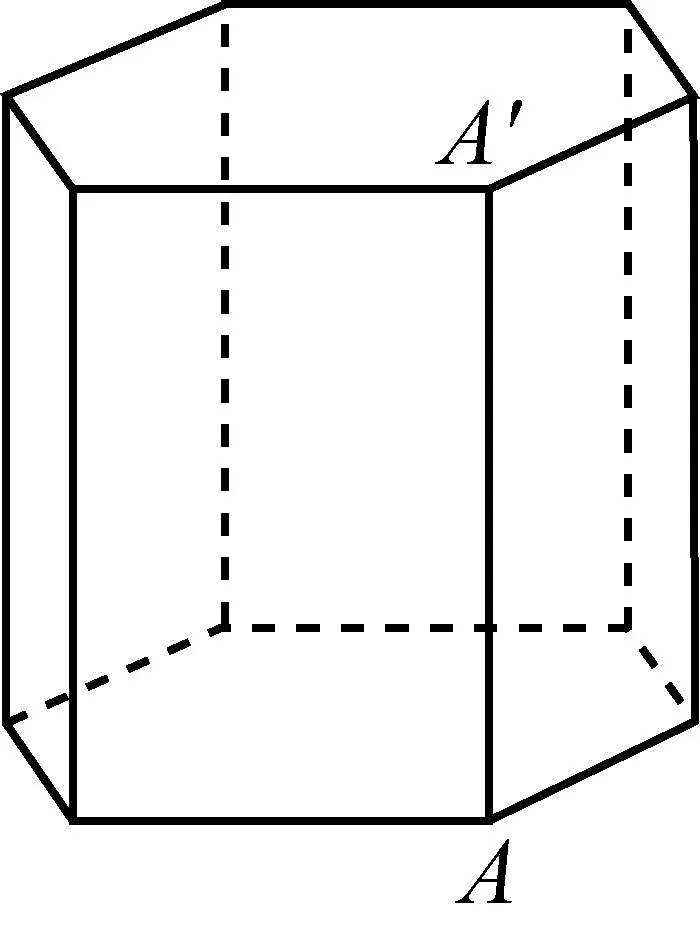
A.4 B.8 C.12 D.16

评析：此题来自于大约成书于公元1世纪的《九章算术》，它的出现标志中国古代数学形成了完整的体系．其内容包括方田、粟米、衰分、少广、商工、均输、盈不足、方程、勾股等九章，全书共有246个问题，每个问题均有给出相当于数学公式的解答.本题以《九章算术》中的“阳马”几何体为为背景，弘扬了中国文化.内容涉及空间点、直线、面的关系等，考察学生的空间想象能力，难度适中.根据题意可知，符合题目要求的面有4个，每一个都有4个顶点，所以选择D.

(2)《张邱建算经》中的“百鸡问题”

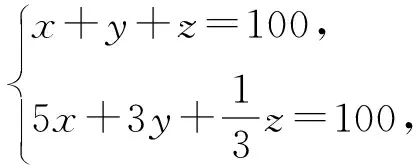
评析：此题源于成书约公元5世纪的数学著作《张邱建算经》，现传本有92问，比较突出的成就有最大公约数与最小公倍数的计算，各种等差数列问题的解决、某些不定方程问题求解等.“百鸡问题”是《张丘建算经》中的一个著名数学问题，它给出了由三个未知量的两个方程组成的不定方程组的解.[5]本题以历史名题为背景，赋予丰富的数学文化内涵.根据题中条件，解答相对较容易，只需将z=81带入原方程组，得到二元一次方程组，求解得x=8，y=11.

1.3 以数学与其他学科的联系为背景

朱载堉和“十二平均律”

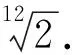
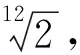
1.4 以实际生产生活的内容为背景

中国古建筑中的榫卯设计

(全国Ⅲ卷 理3文3)中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是

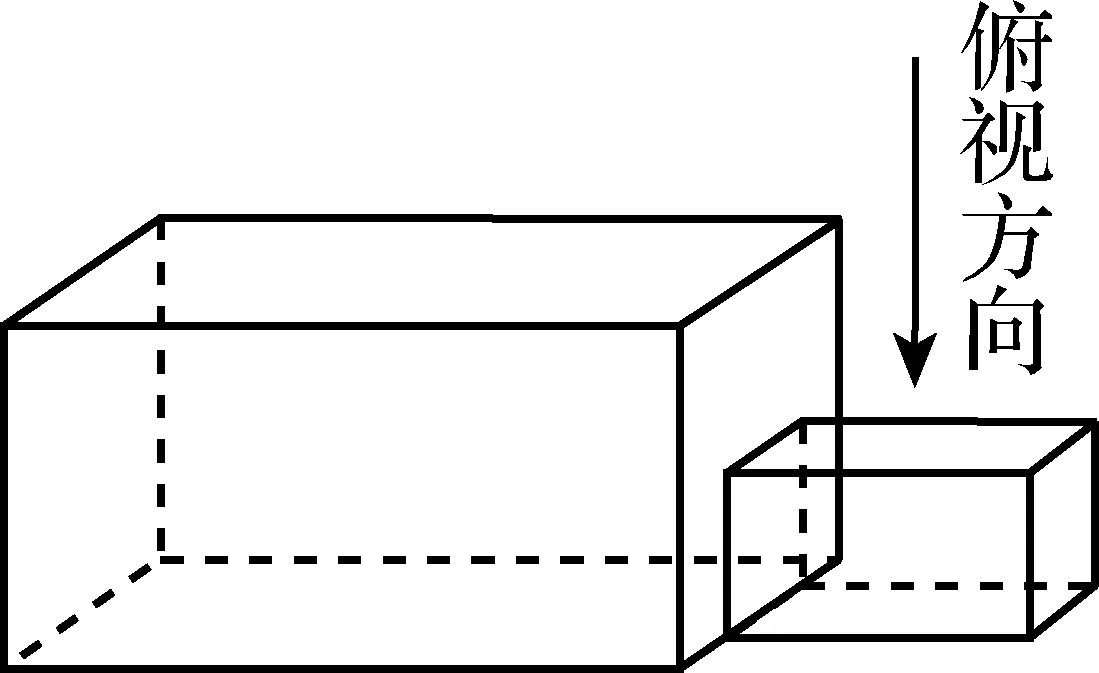
评析：本题以中国古建筑借助榫卯连接木构件为背景，很好地考查了三视图的相关内容，考生需要先观察卯眼的直观图，再想象其俯视图，这和以往多数通过所给三视图想象直观图的命题方式相比，确实增添了一些新意，另外也传播了中国悠久的文明和智慧.题目整体来说比较简单，观察图形后可知其俯视图为A.

2 数学文化教学建议

随着数学文化类高考试题的应运而生，数学文化也因此渐入高中数学课堂.数学文化具有比数学知识体系更为丰富和深邃的文化内涵，数学文化是对数学知识、技能、能力和素养等概念的高度概括.那么，我们该如何把数学文化渗透到日常教学呢？在数学教学实践中，进行数学文化教学的可借鉴的方法有：讲述数学家的趣闻轶事；介绍知识的起源和发展过程；建立数学与其他学科的联系；寻找生活中的数学.

2.1 讲述数学家的趣闻轶事

数学是一门系统性和逻辑性都很强的学科，如果缺乏形象性和生动性.学生在学习时容易觉得枯燥乏味，产生厌烦心理.在教学过程中，教师将一些有趣的或有启发性的数学家的故事融入教学活动中，能够吸引学生的注意力，引发学生学习数学的兴趣.比如，三角学是在天文历法中发展起来的，具有较为深远的历史渊源，在讲授这部分内容时，为激发学习兴趣，教师可以嵌入一些相关的趣味史料.据说9世纪阿拉伯数学家、天文学家比鲁尼曾通过测量并使用三角学计算出了地球半径.[7]

2.2 介绍知识的起源和发展过程

有些数学知识的形成和发展过程具有一定的人文背景，通过介绍知识的起源和发展过程，既可以激发学生学习数学的热情，又可以使学生感受数学知识浓厚的历史文化底蕴.例如在对数教学过程中，可以介绍纳皮尔发明对数的历史过程，当时，哥白尼的“日心说”刚刚流行，天文学成为当时热门学科.为了简化天文学中大量繁杂的计算，纳皮尔经过潜心研究，发明了对数.[8]

2.3 建立数学与其他学科的联系

为了让学生能够更深刻的理解数学知识的内涵，了解数学知识的广泛应用，激发学生主动学习的兴趣，在数学教学过程中，教师可以尝试将数学与历史、科学、哲学、社会科学、艺术、音乐、文学、逻辑学等学科联系.使得不同学科知识成为一个整体，学生也能够更有效地学习数学.Edwards认为，在高中阶段，将文学与数学联系起来，可以提高学生的阅读能力，促进跨学科学习.他在函数、统计、三角等知识点的教学中，运用数据分析方法检验莎士比亚十四行诗；在讲授统计假设检验时，让学生运用相关知识来研究莎士比亚是否是爱德华·德·维尔的笔名；并利用软件统计莎士比亚诗句的长度、出现的频率等.该探究活动激发了学生的浓厚兴趣.[9]

2.4 寻找生活中的数学

数学的特点之一就是具有广泛的应用性.知识来源于生活，在数学教学过程中，教师可以尝试以实际生活为背景， 将数学知识融入学生身边的

例子，以激发学生的学习兴趣.Mahoney根据每个人的指纹以及掌心的曲线不一样的，且这些曲线都对应于数学上的某种函数，包括多项式函数、幂函数、指数函数、对数函数、正弦函数等设计了“掌上数学”的教学活动，学生对此十分感兴趣.[10]

在数学教学过程中应根据实际需要，充分挖掘数学文化内容，将其渗透到日常教学中，就让学生逐渐爱上数学学习.但是，数学文化的渗透不能喧宾夺主，影响正常教学内容的的学习.如何把握渗透数学文化的“度”的问题，需要数学教师在教学过程中仔细思考.