锂电池在电压平台期荷电状态估算研究

张康康 郑晓彦 高金辉

摘 要： 电池的荷电状态（SOC）是指电池剩余电量占总容量的比例。对荷电状态的测量是通过对电池电压和电流等数据的间接分析，这一过程不可避免地会出现噪声的干扰，进而对估计结果造成严重影响。在此采用人工神经网络的电池模型来估计电池SOC，再利用无迹卡尔曼滤波算法来减少神经网络估计电池SOC的误差。通过仿真结果与真实值之间的比较证明了该模型具有准确预测电池荷电状态的性能。

关键词： 荷电状态（SOC）； 神经网络； 无迹卡尔曼滤波； 电压平台期； 噪声干扰； 电池剩余电量

中图分类号： TN36?34； TM912 文献标识码： A 文章编号： 1004?373X（2018）20?0150?03

Abstract： The state of charge （SOC） of the battery is the ratio of the remaining battery capacity to the total capacity. The SOC measurement is conducted by means of indirect analysis for voltage and current data of the battery， but noise interference is inevitable in this process， which has a serious impact on estimation results. The battery model based on artificial neural network is adopted to estimate the SOC of the battery. The unscented Kalman filter （UKF） algorithm is used to reduce battery SOC estimation errors of neural network. The comparison of the simulation results and real values proves that the model can accurately predict the SOC of the battery.

Keywords： SOC； neural network； unscented Kalman filter； voltage plateau； noise interference； remaining battery capacity

能源危機以及环境恶化对传统的汽车发展的影响越来越大，因此电动汽车得到了大家的广泛关注。动力电池组作为电动汽车的重要组成部分，需要对电池进行严格的管理和控制。

估算电池荷电状态（SOC）是电池管理系统最基本也是最重要的功能之一，系统中的许多其他功能都依赖于电池荷电状态评估的结果。

1 电压平台期

如图1所示是磷酸铁锂的开路电压?荷电状态（OCV?SOC）曲线。对于磷酸铁锂电池，开路电压曲线在一些区域（3.2 V左右之前）十分平缓，这就是电压平台期。图中中间部分的曲线几乎达到了完全的水平。在这区域附近，随着电池的充放电，电池可以维持相对稳定的开路电压，进行SOC估算会有很大的误差[1]。

2 神经网络模型

神经网络是智能的计算工具，对于系统模型，它有着广泛的应用。神经网络可以拟合非线性函数并使它们适合于复杂系统模型。神经网络可以学习和更新内部结构从而适应变化的环境。神经网络由输入层、隐含层和输出层组成，如图2所示。输入层表示输入变量；一个或多个隐含层用以连接系统输入和输出之间的非线性；输出层表示系统的输出变量[2]。

图2用于SOC估计的前馈神经网络结构。神经网络的输入变量分别为电流（I）、电压（V）和温度（T），并且输出是电池的SOC。相邻两层之间的节点是相互连接的，输出层通过权值传递给输入值。隐含层和输出层是在每个节点上具有激活函数的处理层[3]。在隐含层中双极S型函数经常被用作激活函数，定义为：

式中：[xi]是前一层i节点的输出；[wij]是相互关联的权值，从前一层的第i个节点到本层的第j个节点；[bj]是偏差。权值[wij]和偏差[bj]需要在训练的基础上确定数据。本文使用反向传播（BP）算法来确定这些参数。反向传播意味着网络训练过程中的错误可以从输出层传播到隐藏层，然后传播到输入层，以估计每个节点的最佳的权值[4]。调整权值可以改变网络的输入误差。神经网络的学习过程是通过对样本的学习，不断修改各层的权值，进而减小输出误差的过程。

在研究中，神经网络的输入是电压和电流的测量值。因为电池中的电容电阻，前一个样品的电流和电压会影响当前电池状态[5]。因此，以前样本的测量值也被输入到神经网络模型中。另外，为了避免神经网络过度训练，每4个样本中选取1个样本进行神经网络的训练。

3 UKF算法

滤波技术已应用于噪声数据的状态估计。无迹卡尔曼滤波（UKF）是一种典型的基于无迹变换（UT）的估计滤波方法，不需要对系统方程进行线性化[6]。UT变换通过确定性采样，采用多个粒子点逼近函数的概率密度分布，进而获得更高阶次的均值和方差，能够对系统进行更准确的估计[7]。

下面讨论UKF的应用步骤[8]。

4 仿真试验和结果分析

神经网络训练可以通过适当的数据归一化来提高效率和鲁棒性。因此，训练之前通过下式将输入数据归一化到区间[0，1]之间：

磷酸铁锂电池通常用于电动汽车。本文使用的测试电池为IFR26650磷酸铁锂电池（LiFePO4），额定容量是2.3 A·h，电压为3.2 V。电池放在温度箱里，并且测量电池的温度，使电池处于25 ℃的温度下构建训练数据。如图3所示是在室温25 ℃测试中经过神经网络估算之后SOC从20%～100%之间的预测值和真实值之间的比较。神经网络计算过程实际上包含了正向和反向传播两个阶段。正向传播过程中，输入信息从输入层经隐含层逐层处理，并传向输出层。如果输出层不能得到期望输入则转入反向传播，将误差信号沿原来的连接通道返回，修改各层神经元的权值，使误差信号最小。

由于磷酸铁锂电池放电特性的平稳性，这些误差主要出现在中间的SOC范围（30%～80%），即电压平台期。在此区域很大的SOC变动才对应极少的电压变化，这对电压的测量影响很大。电压测量的不精确直接影响到神经网络估计电池SOC的精确度[9]。这个问题不能通过更多的隐含层和训练神经网络来解决，以降低均方根误差，因为存在过度拟合神经网络的风险。如果神经网络被训练成一个太低的均方根误差，它可能失去泛化能力。在电动汽车（EVs）的使用中，应当避免SOC估计值在实际值附近突然跳跃或下降，迷惑使用者[10]。为了能够提供足够精确的平滑估计，本文采用UKF处理神经网络在电压平台期的输出，并滤除误差。如图4所示是在室温25 ℃神经网络估算之后再经过无迹卡尔曼滤波之后SOC从20%～100%之间的预测值和真实值之间的比较。实体曲线被看作是较实际的SOC。从图中明显可以看到，经过UKF对神经网络输出进行滤波，明显使得SOC估计值精确且平滑。

5 结果与讨论

式中：yk是样本k的真实值；tk是相应的预测值。从表中可以看到，SOC估计在25 ℃通过单独神经网络方法生成的均方根误差为2.5%，最大误差为14.4%。UKF降噪后，均方根误差降到1.3%，并且最大误差降到2%。因此，UKF是减少神经网络SOC估计误差的有效方法。

6 结 论

本文提出一种基于前馈神经网络和无迹卡尔曼滤波（UKF）算法估计SOC的方法。为了估计电池SOC，神经网络的输入为电压、电流和温度，输出为SOC。此时SOC估算误差比较大，所以为了进一步提高估计精度，采用一种基于UKF的神经网络误差估算方法。经过UKF滤波后，均方根误差和最大误差均比较小，从而起到了精确估计电池SOC的目的。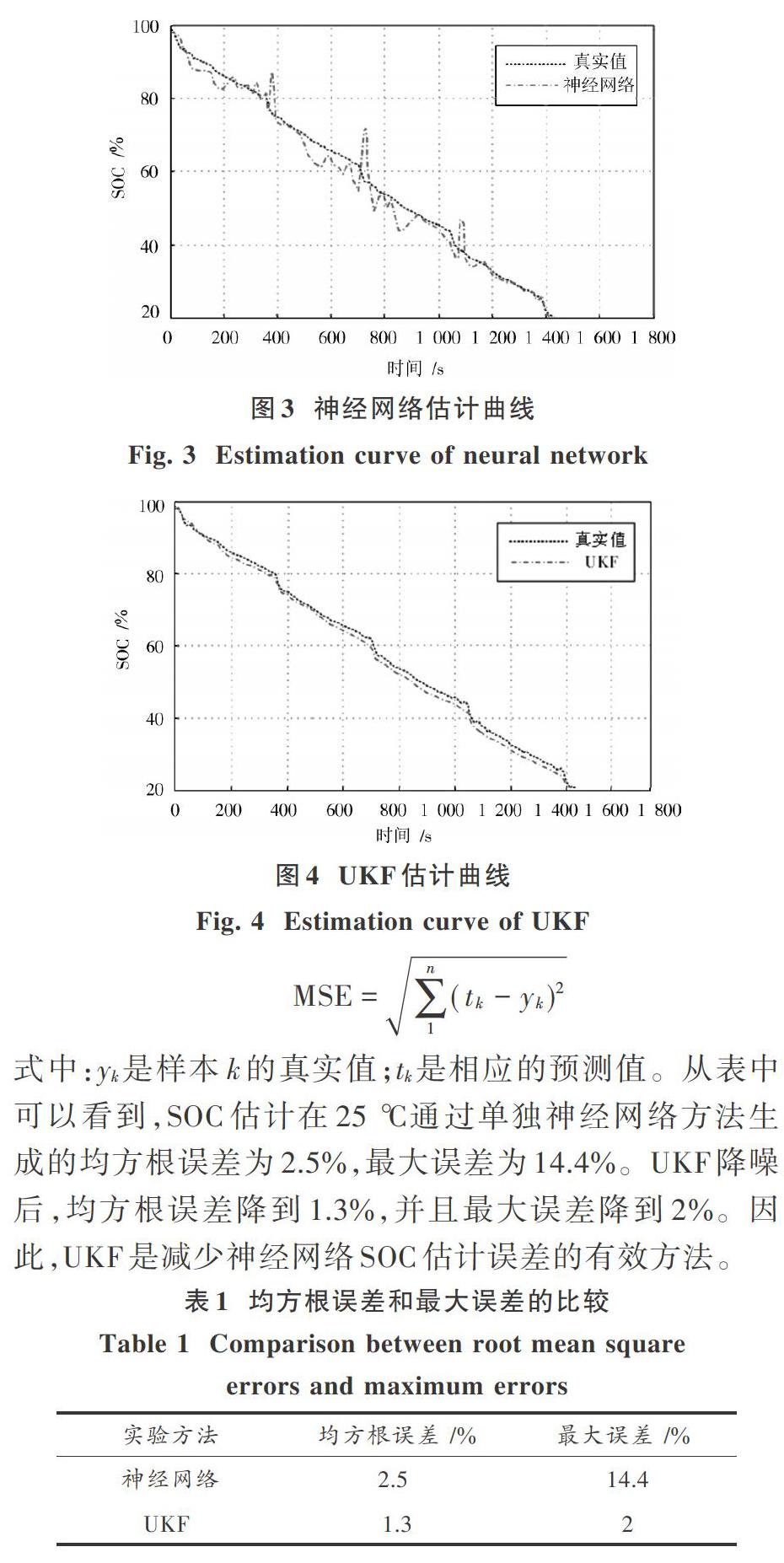

注：本文通讯作者为高金辉。

參考文献

[1] 高金辉，巴雁远.OCV处于平台期的汽车锂电池SOC估算的研究[J].现代电子技术，2017，40（10）：175?177.

GAO Jinhui， BA Yanyuan. Study on lithium battery SOC estimation during plateau of OCV [J]. Modern electronics technique， 2017， 40（10）： 175?177.

[2] 尹安东，张万兴，赵韩，等.基于神经网络的磷酸铁锂电池SOC预测研究[J].电子测量与仪器学报，2011，25（5）：433?437.

YIN Andong， ZHANG Wanxing， ZHAO Han， et al. Research on estimation for SOC of LiFePO4 Li?ion battery based on neural network [J]. Journal of electronic measurement and instrumentation， 2011， 25（5）： 433?437.

[3] BASHEER I A， HAJMEER M. Artificial neural networks： fundamentals， computing， design， and application [J]. Journal of microbiological methods， 2000， 43（1）： 3?31.

[4] 毛华夫，万国春，汪镭，等.基于卡尔曼滤波修正算法的电池SOC估算[J].电源技术，2014，38（2）：298?302.

MAO Huafu， WAN Guochun， WANG Lei， et al. Estimation of battery SOC based on Kalman filter correction algorithm [J]. Chinese journal of power sources， 2014， 38（2）： 298?302.

[5] KANDEPU R， FOSS B， IMSLAND L. Applying the unscented Kalman filter for nonlinear state estimation [J]. Journal of process control， 2008， 18（7）： 753?768.

[6] PARTHIBAN T， RAVI R， KALAISELVI N. Exploration of artificial neural network （ANN） to predict the electrochemical characteristics of lithium?ion cells [J]. Electrochimica Acta， 2008， 53（4）： 1877?1882.

[7] 胡志坤，刘斌，林勇，等.电池SOC的自适应平方根无极卡尔曼滤波估计算法[J].电机与控制学报，2014，18（4）：111?116.

HU Zhikun， LIU Bin， LIN Yong， et al. Adaptive square root unscented Kalman filter for SOC estimation of battery [J]. Electric machines and control， 2014， 18（4）： 111?116.

[8] 高金辉，杜浩.电动汽车锂电池组的新型双向均衡法[J].河南师范大学学报（自然科学版），2016，44（6）：53?56.

GAO Jinhui， DU Hao. A new bi?directional equalization method for lithium?ion battery pack in electric vehicles [J]. Journal of Henan Normal University （Natural science edition）， 2016， 44（6）： 53?56.

[9] HU C， YOUN B D， CHUNG J. A multiscale framework with extended Kalman filter for lithium?ion battery SOC and capacity estimation [J]. Applied energy， 2012， 92（4）： 694?704.

[10] 高金辉，苏明坤.基于神经网络的自适应滤波研究[J].河南师范大学学报（自然科学版），2013，41（1）：47?49.

GAO Jinhui， SU Mingkun. Adaptive filter based on neural networks [J]. Journal of Henan Normal University （Natural science edition）， 2013， 41（1）： 47?49.