风载荷下支柱瓷绝缘子的弯曲应力计算

(北京工商大学材料与机械工程学院，北京100048)

0 引言

在我国，支柱瓷绝缘子已经广泛应用于隔离开关中[1]。在强风地区，室外隔离开关中的支柱瓷绝缘子要承受极大的风载荷及其他工作载荷，这些载荷会在支柱绝缘子上产生弯曲应力。在设计中对风力的影响考虑不够是支柱绝缘子断裂的原因之一[2]。支柱绝缘子一旦发生断裂，将会引发接地故障，从而造成电网事故。同时还伴随着电击和零部件坠落，很有可能危及人身安全，后果极其严重[3]。因此研究在风载荷作用下支柱瓷绝缘子的机械强度、计算其弯曲应力就显得尤为重要。

在实际的户外，绝缘子所受的风载荷一般不是一个恒定的静载荷，而是一个大小和风向时刻变化的动载荷。因此绝缘子承受的是交变的弯曲应力，在很多情形下会发生疲劳失效进而引起断裂[4-5]。但由于脉动风的随机性很强，因此要通过仿真计算来校核绝缘子在该动载荷下的疲劳强度是非常困难的。通常的做法是将作用在绝缘子上的风载荷简化为对应于某一风速的恒定静载荷[6]，从而计算此时绝缘子上的静应力。由于瓷绝缘子由脆性材料制成，而脆性材料的抗拉能力比抗压能力弱很多。因此当支柱绝缘子承受风载荷等横向载荷时，其上的最大弯曲拉应力才是影响其机械强度的主导因素。

就现有的研究，主要有三种方法来计算绝缘子在风载荷作用下的弯曲应力。第1种方法就是通过FLUENT软件对风吹过绝缘子的情形进行流体动力学仿真，以求得在绝缘子表面的风压分布[7-8]。然后将此风压分布输入ANSYS中的Static Structural模块进行静力学仿真，即可得到绝缘子上各点处的弯曲应力以及应变和变形量。目前只有文献[5]提到了这种计算方法，但并未给出弯曲应力的分布云图和具体数值，只仿真了风速为45 m/s的情形，且仿真的几何模型只包含部分伞裙，没有包括整个绝缘子。

第1种方法虽然很准确，但一般来讲，流体动力学仿真的计算量比较大，而且迭代不容易收敛。因此大部分的研究都是采用第2种方法。即采用如下经验公式或其他公式来对风载荷进行估算[9-10]。

(1)

式中：F是绝缘子承受的风载荷，u是来流的风速，A是绝缘子的受风面积。文[8]认为对于风速超过25 m/s的情形，公式(1)的计算结果高估了风载荷。基于FLUENT软件仿真的结果，将公式(1)修正为

(2)

在采用上述公式确定风载荷后，将其看作为一个集中力，施加在支柱绝缘子的顶部[11]，然后通过ANSYS软件的静力学模块来仿真计算绝缘子上的静应力。相比于第1种方法，第2种方法的仿真计算量比较小。但采用该方法进行仿真时忽略了在绝缘子表面风压分布的不均匀性，因此会给弯曲静应力的计算结果带来一定的偏差。这个偏差到底有多大目前还不确定，也未见有任何这方面的研究。

第3种方法是将支柱绝缘子简化为一个一端固定另一端自由的长圆柱体，其上受均布风压的作用，然后按悬臂梁的弯曲正应力公式进行计算。文献[12]利用ANSYS软件仿真计算了一端受到横向力的支柱绝缘子上的弯曲应力，然后将仿真结果与第3种方法的计算结果相比较，以分析伞裙形状所引起的应力集中对绝缘子上弯曲应力的影响。

笔者将分别采用上述三种方法来计算支柱瓷绝缘子在风载荷下的弯曲应力，并给出最大弯曲拉应力随风速的变化规律。支柱绝缘子除了能承受风载荷以外，还要能够承受一定的来自于导线拉力等其他的横向载荷[13]，这将会增大绝缘子上的弯曲拉应力,其最大值有可能会超过绝缘子材料的许用应力。因此本文还将根据弯曲正应力强度条件，计算在不同风速下支柱瓷绝缘子可以承受的除风载荷之外的最大工作载荷。

由于第1种方法考虑了支柱绝缘子表面所受的不均匀分布的风压，而且也考虑其表面真实的结构形状，其力学模型与风载荷下支柱绝缘子的实际情况最接近。因此对上述三种方法的计算结果进行比较时，采用第1种方法的计算结果作为比较的基准，其他两种方法的计算结果与其的差值或相对差值在本文里被称为偏差或相对偏差。

在设计支柱绝缘子时，除了要计算最大弯曲拉应力的大小，还需要确定其所在的位置。最大弯曲拉应力所在的位置常常是引起绝缘子疲劳失效的初始微裂纹的发源地，因此也是最易发生断裂的地方，在设计和制造工艺中应引起足够的重视。文[3]的仿真计算结果表明，对于无内部缺陷的支柱瓷绝缘子，最大应力发生在倒数第一伞裙下圆弧与瓷柱表面相切处。文[6]ANSYS仿真的结果显示最大弯曲拉应力发生在隔离开关支柱瓷瓶下法兰口附近。文[12]仿真计算所得最大弯曲应力发生在绝缘子下部与下法兰盘接触的地方，与文[6]的结果相近。但其实验所得最大值发生在靠近下法兰盘的第一和第二伞裙之间的瓷柱表面。文[14]研究了串联在一起的上、下两节支柱绝缘子的应变，其仿真计算和实验结果都表明最大应变发生在下节绝缘子下端第一片和第二片伞裙之间的瓷柱上，故推测此处应力集中最严重，最易发生瓷绝缘子断裂事故。由此可见各研究在这个问题上说法不一，将在最后将结合自己的仿真结果对此问题进行探讨。

1 支柱绝缘子在风载荷下的力学模型

图1所示是某型户外单臂双柱并列式隔离开关，其中的每一支柱绝缘子分别由上、下两节瓷绝缘子串联组成。因为绝缘子整体的机械强度很大程度上取决于单节绝缘子的强度，因此本文只研究单节支柱绝缘子在风载荷下的弯曲应力计算方法。其几何形状和尺寸如图2所示。所计算的风速分别为10 m/s、20 m/s、30 m/s、40 m/s、50 m/s、60 m/s和70 m/s，风速方向始终与绝缘子的轴线保持垂直。

图1 户外单臂双柱并列式隔离开关Fig.1 Outdoor single-armdisconnecting switch with two paralleled posts

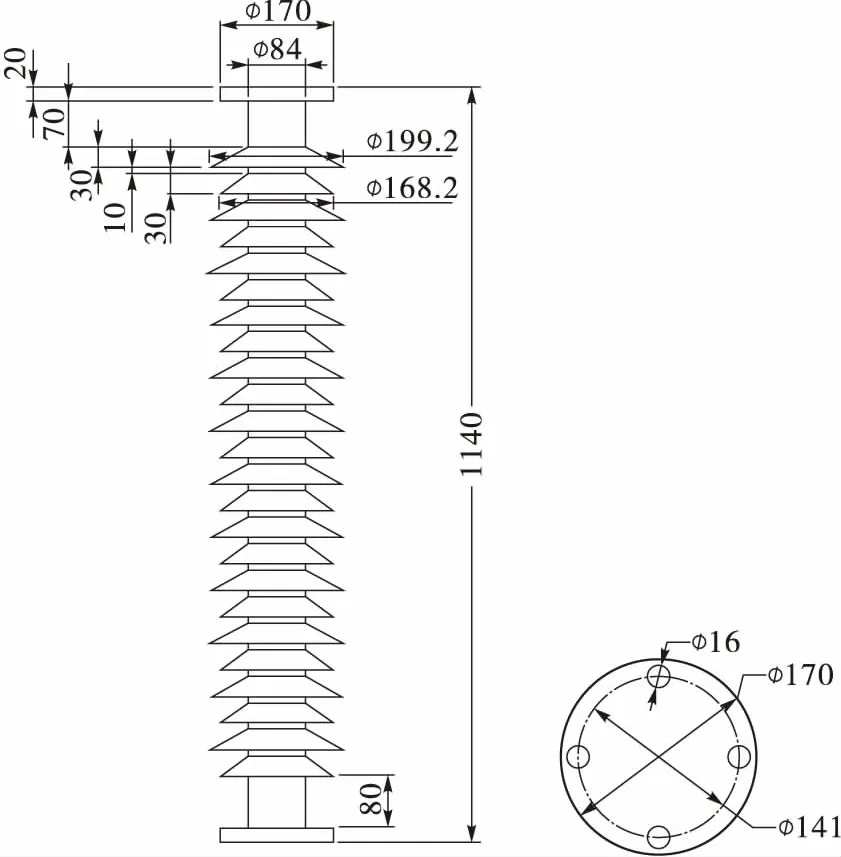
图2 支柱瓷绝缘子的结构和尺寸Fig.2 Structure and dimension of porcelain post insulator

1.1 第1种计算方法

首先采用湍流模型中的k-ε两方程模型[15]，通过FLUENT软件对支柱绝缘子周围的风场进行计算流体动力学仿真，以求出在不同风速下绝缘子表面的风压分布。具体的建模过程、网格划分及各参数设置详见文[8]，在此不再赘述。

然后开始进行静应力仿真计算。首先在ANSYS软件的Workbench平台里，建立一个Static Structural功能模块。在该模块的第一步Engineering Data里输入瓷体材料的性能参数[16]，如表1所示。将上述绝缘子的几何模型导入该模块的第二步Geometry，然后在第三步Model中划分网格，如图3所示。接着将FLUENT仿真所得的风压分布导入第四步Setup中进行加载，并在该步设置边界条件，即绝缘子的下法兰固定，上法兰自由。绝大多数研究在仿真时都是将下法兰的底部端面设为固定面，即下法兰底面上的所有点在各个方向上的自由度都受到全约束[3,6,12]。但本文是将下法兰中的四个螺栓孔柱面设为固定面，认为这样处理更接近绝缘子下端实际的固定状态。最后在第五步Solution进行仿真计算，在第六步Results即可获得绝缘子上的应力、应变及变形量的分布云图和数值大小。

表1 瓷体材料的力学性能Table 1 Mechanical properties of porcelain material

图3 支柱绝缘子在静应力仿真计算中的网格划分Fig.3 Meshing of post insulator for simulation and calculation of static stress

1.2 第2种计算方法

不用对绝缘子周围的风场进行计算流体动力学仿真，而是直接采用前述公式(2)计算出对应于某一风速的风载荷。并将风载荷等效为一个集中力作用在支柱绝缘子上法兰的顶面，其方向与风速的方向一致。这相当于将绝缘子所受的风压折算到其顶部，为保证折算后在固定端的弯矩仍保持不变，所施加的集中力应等于由公式(2)算出的风载荷的一半[17-18]。

然后在ANSYS软件的Workbench平台里，建立一个Static Structural功能模块进行静应力仿真计算，其余各步骤与第1种方法基本相同，只是在第四步Setup中，不需要将风压分布导入，而是直接按上述方法在上法兰的顶面加载一个集中力。另外网格划分及固定面也与第1种方法相同。

1.3 第3种计算方法

将支柱绝缘子简化为一个直径等于瓷柱直径、下端固定、上端自由的悬臂梁。采用前述公式(2)计算出对应于某一风速的风载荷。将风载荷看成是一个均布载荷，其方向与风速的方向一致。其最大弯曲拉应力σmax的计算公式为[19]

(3)

式中的Mmax是在绝缘子固定端的弯矩，W是瓷柱横截面的抗弯截面系数，F是绝缘子所受的风载荷，l是绝缘子的总高度，d是瓷柱的直径。代入图2所示绝缘子的几何尺寸，可得：

σmax=9.796×10-3F(MPa)

(4)

1.4 计算除风载荷以外的最大工作载荷

支柱绝缘子的弯曲正应力强度条件为其最大弯曲拉应力σmax不能超过材料的许用拉应力。即

(5)

式中：[σ]是在绝缘子材料的许用拉应力，σb是绝缘子材料的抗拉强度极限，n是安全因数。文[4]建议对支柱绝缘子抗弯强度计算，安全因数取2.0，文[16]按照盘式瓷绝缘子将安全因数取为2.7，文[20]认为脆性材料的安全因数一般取2.5～3.0。综上所述，本文对于支柱瓷绝缘子，其安全因数取为n=2.5。利用弯曲正应力强度条件公式(5)，采用前述三种弯曲应力的计算方法就可以分别得出不同风速下支柱绝缘子所能承受的除风载荷之外的最大工作载荷。假定该载荷为作用在支柱绝缘子上法兰顶面的集中力，与绝缘子的轴线垂直，与风速方向相同。

2 计算结果与分析

图4显示的是当风速为60 m/s时，由第1种和第2种计算方法分别仿真所得的在支柱绝缘子下部的弯曲正应力分布情况。可以看出两种计算方法的仿真结果都显示最大的弯曲拉应力发生在瓷柱下部表面与下法兰接触的地方。

图5给出了由这三种计算方法分别得到的最大弯曲拉应力随风速的变化规律。可以看出随着风速的增大，支柱绝缘子的最大弯曲拉应力也随之增大，而且风速越高，最大弯曲拉应力增大的速率也越快。第2种计算方法仿真所得的最大弯曲拉应力比第1种方法的仿真结果要略高一些。但总的来说，二者吻合较好，最大的相对偏差只有8.3%。这说明采用第2种方法来仿真计算支柱绝缘子在风载荷下的弯曲应力还是比较经济实用的。既能省去由FLUENT流体动力学仿真带来的巨大计算量，又能得到偏差不大的计算结果，同时还能正确地判断出发生最大弯曲拉应力的危险点位置。从图5还可以看出，第3种方法计算所得的最大弯曲拉应力比1种方法的仿真结果小很多，其偏差非常大。这说明支柱瓷绝缘子的弯曲应力模型不能简化为长圆柱体的悬臂梁模型。

图6给出了都采用第1种方法，但按三种不同固定面分别仿真得出的最大弯曲拉应力随风速的变化规律。这三种固定面是指绝缘子下法兰的四个螺栓孔柱面、下法兰的底部端面和瓷柱的底部端面。显然如果将下法兰或瓷柱的底部端面作为固定面，则仿真所得的最大弯曲拉应力要偏小很多，这会过分高估支柱绝缘子的抗弯强度。因此在仿真时，不仅要采用正确的计算方法，而且还要选择合适的约束面设置为固定面。对于后者要注意两点，首先应该将绝缘子组件固定处与力学强度相关的细部结构保留在仿真的几何模型中，此外应根据实际情况采用那些真正被全约束的接触面作为固定面，不能笼统地都采用底部端面作为固定面，否者仿真计算结果的偏差会很大。

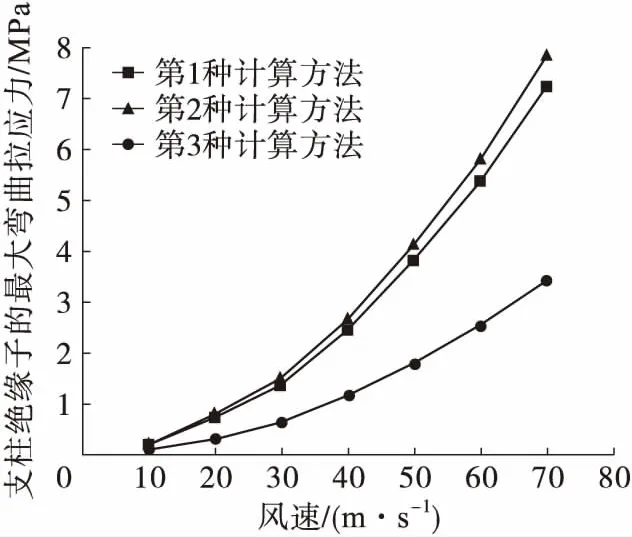
图5 支柱绝缘子的最大弯曲拉应力与风速的关系Fig.5 Relationship of maximum tensile bending stress of post insulator with wind speed

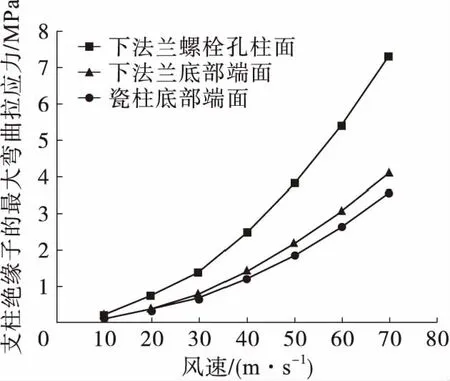
图6 采用第1种方法按不同固定面仿真所得 最大弯曲拉应力与风速的关系Fig.6 Relationship of maximum tensile bending stress with wind speed simulated by the 1st method for different mounting surfaces

图7显示了由弯曲正应力强度条件算出的支柱瓷绝缘子所能承受的除风载荷之外的最大工作载荷随风速的变化规律。可以看出当风速超过30 m/s时，随着风速的增大，支柱瓷绝缘子承受其他工作载荷的能力急剧下降。采用第3种方法的计算结果过分地高估了支柱绝缘子的承载能力，这再次说明其弯曲应力的计算模型不能简化为长圆柱体的悬臂梁模型。第2种方法的仿真结果与第1种方法的结果吻合很好，在风速为70 m/s时，前者比后者低3.5%。由此看出第2种方法可以准确地仿真得到支柱瓷绝缘子的抗弯能力。

图7 支柱绝缘子能承受除风载荷之外的最大 工作载荷与风速的关系Fig.7 Relationship of maximum work load applied on post insulator excluding wind load with wind speed

以往的一些研究通过力学仿真或实验得出结论，认为在支柱绝缘子下部，伞裙根部的应力集中很严重，因此最大的弯曲应力发生在下部第一和第二伞裙之间的瓷柱表面或第一伞裙与瓷柱表面相接处，这与本文的仿真结果有差异。不同研究在这个问题上得出不同的结论可能是由以下几个原因造成的。首先所研究的支柱绝缘子的几何形状和尺寸大小有差异，造成严重应力集中的部位就不一样。比如本文和文[12]研究的是单节绝缘子，而文[14]研究的是上、下两节绝缘子串联在一起的组件。其次，力学仿真的几何模型与实际实验的绝缘子不完全一致。比如文[12]仿真的几何模型除绝缘子外还包含法兰，但实际测量的试件是瓷件，不包含法兰。因此其仿真所得最大弯曲应力所在的位置与实验结果不同。第三，各研究在绝缘子上的加载方式也不尽相同。文[6]在仿真模型里不仅考虑了与绝缘子轴线垂直的横向载荷，还考虑了作用其上的扭矩，而其他研究都没有考虑扭矩。第四，伞裙与瓷柱表面相接处的应力集中固然会使得该处的应力增大，但也许不是产生最大弯曲拉应力的唯一或主要的原因。实际上，支柱绝缘子下部固定面位置的不同对弯曲拉应力的分布也有很大的影响。

图8显示了当固定面分别为下法兰的底部端面和瓷柱的底部端面，在风速为60 m/s时，由第1种方法仿真所得在支柱绝缘子下部的弯曲正应力分布情况。可看出，当固定面为下法兰底部端面时，除了在瓷柱下部与下法兰相接处之外，在下部第一和第二伞裙之间的瓷柱表面也出现了少量的高弯曲拉应力区。当固定面为瓷柱底部端面时，在后者出现的高弯曲拉应力区范围变大很多。而图4(a)则显示，当固定面为下法兰的四个螺栓孔柱面时，高弯曲拉应力区只唯一地出现在瓷柱下部与下法兰相接处。可能正是由于以往的一些研究在仿真计算或实验中采用支柱绝缘子的下法兰或瓷柱的底部端面作为固定面，才使得他们认为伞裙根部的应力集中造成了最大弯曲拉应力出现在绝缘子下部第一和第二伞裙之间的瓷柱表面。

在文[3]中提到，统计发现支柱瓷绝缘子的断裂故障95%以上都发生在法兰口内3 cm到第一伞裙之间。文[6]认为隔离开关支柱瓷瓶下法兰口附近的应力集中与实际隔离开关支柱瓷瓶断裂的重点部位相符。文[21]指出有数据表明，支柱瓷绝缘子断裂多发生在下法兰和第一瓷沿之间。文[22]的弯曲破坏负荷试验表明所检测的三柱支柱瓷绝缘子的断裂部位均在下节元件的下法兰附近。这些研究表明本文仿真所得支柱瓷绝缘子的最大弯曲拉应力发生在瓷柱下部表面与下法兰相接处的结论应该是合理的。

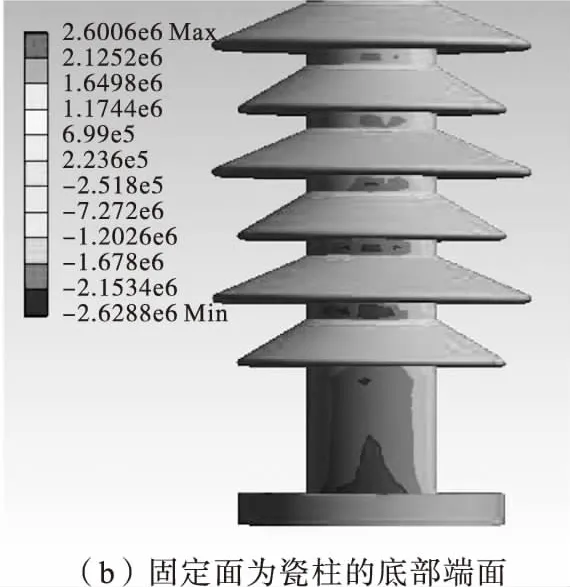
图8 风速为60 m/s时采用第1种方法按两种固定面 得出的弯曲正应力分布Fig.8 Normal bending stress distribution by the 1st method for two kinds of mounting surfaces when wind speed is 60 m/s

3 结语

阐述了三种计算风载荷下支柱瓷绝缘子上弯曲应力的方法。通过这三种方法分别给出了绝缘子上最大弯曲拉应力随风速的变化规律。然后采用第1种方法，按三种不同的固定面，分别仿真计算了绝缘子上最大弯曲拉应力随风速的变化规律。接着按照弯曲正应力强度条件通过上述三种方法分别计算了在不同风速下，支柱瓷绝缘子所能承受的除风载荷之外的最大工作载荷。最后结合本文的仿真计算结果，分析探讨了不同研究关于最大弯曲应力发生位置得出不同结论的原因。本文的研究结果表明：

1)在风载荷作用下，支柱瓷绝缘子的最大弯曲拉应力随风速的增加而增大，风速越高，随之增大的速率也越快。当风速超过30 m/s时，随着风速的增大，支柱瓷绝缘子所能承受的除风载荷之外的最大工作载荷急剧减小。

2)第2种方法仿真所得风载荷下的最大弯曲拉应力以及所能承受的除风载荷之外的最大工作载荷，都与第1种方法的仿真结果吻合很好。而第3种方法所得计算结果的偏差很大，说明支柱绝缘子的弯曲应力计算模型不能简化为长圆柱体的悬臂梁模型。

3)按第1种方法，将下法兰或瓷柱的底部端面作为固定面，仿真所得的最大弯曲拉应力比将下法兰的螺栓孔柱面设为固定面所得的结果要小很多。因此在对支柱绝缘子进行仿真时，不仅要采用正确的计算方法，而且还要选择合适的约束面设置为固定面。

4)支柱瓷绝缘子在风载荷下的最大弯曲拉应力发生在瓷柱下部表面与下法兰相接触的地方。所研究的支柱绝缘子的几何形状和尺寸大小各异，仿真的几何模型与实际测量的试件不一致，加载方式有差异以及固定面不同等可能是造成以往的研究得出最大弯曲应力发生位置各不相同的原因。