基于动态灵敏度的数控机床立柱优化设计

方 浩，王彦伟

武汉工程大学机电工程学院，湖北 武汉 430205

数控机床的工作性能及数控机床产品质量的好坏与数控机床动态性能息息相关。立柱连接主轴箱和床身，是数控机床的核心结构，影响数控机床刚度，要确保整个数控机床的动态性能，必须首先保证立柱具有良好的动态性能［1］。所以提高数控机床立柱的动静态特性，对于保证加工零件的精度有重要意义。

机床结构优化方法众多，以元结构思想优化为主的结构设计在工程中得到广泛应用［2］；王孚懋等［3］在 B-E（Bernoulli-Euler）梁有限元理论指导下，创建机床弹性轴动力学模型，并在MATLAB中求出弯曲振动的固有频率；刘成颖等［4］为得出对机床低阶频率和振型影响最大的构件，对机床进行模态分析，分析了机床的各阶固有频率与振型；HUANG等［5］应用有限元方法，找到了辨识整机静刚度薄弱环节的方法；于长亮等［6］通过对机床动刚度进行分析，辨识出不同模态下整机的薄弱环节；张兴朝等［7］采用有限元法分析了机床的支腿和横梁等多种元结构的动态特性，通过比较分析，选择较好的元结构用于立柱的整体结构设计，效果显著。同时，根据立柱尺寸变化对立柱动态特性的影响，对龙门式立柱整体外形进行了优化设计。在以往对立柱动态性能的结构优化研究中，大多都忽略了立柱动态结构特性的灵敏度分析，使得优化设计存在非最优性和盲目性［8］。

本文以数控机床立柱结构动态特性灵敏度分析为基础，运用有限元分析方法，对立柱进行优化设计，在保证立柱动态性能的同时，减少立柱的重量。

1 立柱的静动力学分析

1.1 立柱有限元模型的建立

有限元分析的第一步是建立有限元模型。但由于工程中涉及到的结构一般比较复杂，通常需要利用CAD软件的三维几何建模功能先创建基于有限元分析的几何模型，然后基于几何模型再创建有限元网格模型［9］。因为数控机床立柱的结构比较复杂，故选择在SolidWorks里对立柱进行三维建模。建模时进行了适当简化，避免因微小特征等引起的网格质量差，计算量大等问题。

简化内容如下［10］：

1）简化模型中的所有微小特征，包括小孔、倒角、倒圆角、凸台等。

2）简化对立柱动、静态特性影响较小的结构。

根据上述要求，建立的数控机床立柱几何模型。其简化后的三维模型如图1所示。

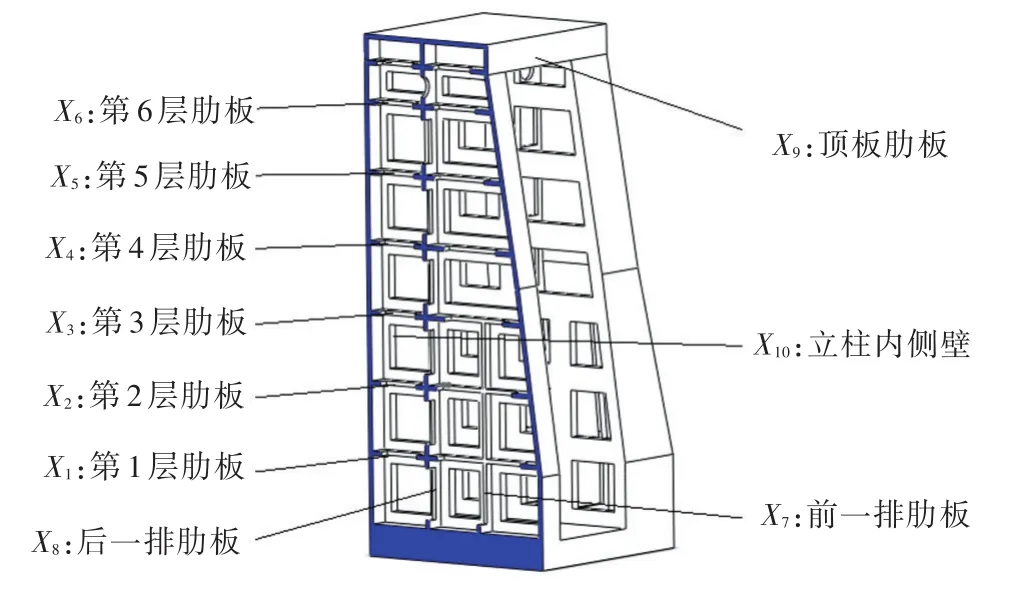
图1 立柱几何模型Fig.1 Model of column geometry

1.2 立柱动静力学分析

1.2.1 切削力计算 加工过程中受力复杂，切削力的大小受到工件材料、刀具几何参数、加工工艺参数等因素的影响，要精确计算出，非常困难。本文在计算机床切削力时，考虑机床在切削时会处于危险工况下，通过查阅参考手册以及借鉴相关文献，通过已有的经验公式计算切削力的大小。此数控机床常用的于铣削加工，故切削力计算公式为：

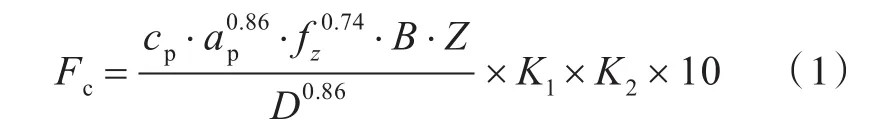
其中：B为切削宽度（mm）；D为铣刀直径（mm）；K1为刀具前角对切削力影响系数；K2为切削速度对切削力影响系数；cp为加工材料的影响系数；fz为每齿进给量；ap为被吃刀量［11］。

取刀具直径D=125 mm，铣刀齿数Z=4，铣削力按一般粗加工计算，B≤52 mm；；ap≤10.4 mm；端面铣刀前角为 +5°；取修正系数K1=1.1。立柱在低速时受铣削力大，故取切削速度为50 m/min，其修正系数K2=1。

将以上数据代入式（1），求取切削力Fc=2 500 N。

1.2.2 静力学分析 数控机床立柱及其相关部件主要包括立柱、主轴箱、滑枕、樘杆。使用ANSYS Workbench自动划分网格，对立柱进行网格划分，选择Mechanical结构分析，设置整个模型的单元尺寸为30 mm。一共划分出172 991个节点，91 840个单元。有限元模型如图2所示。

图2 立柱有限元模型Fig.2 Finite element model of column

数控机床立柱的受力比较复杂，为了便于分析，将立柱的受力简化。立柱受到自身重力；主轴箱、滑枕、樘杆等部件的重力；数控机床工作时所受到的切削力。立柱底部由螺栓固定于床身上，将其近似于固定约束。立柱受力如图3所示。其中，A为固定约束，B为切削力，C为重力。静力学分析结果如表1所示。

表1 静力学分析结果Tab.1 Results of static analysis

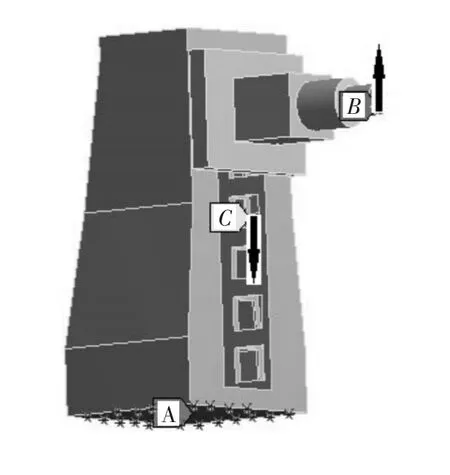
图3 立柱受力图Fig.3 Diagram of column stress

对数控机床立柱进行静力学求解，得到图4和图5。

图4 立柱总变形云图Fig.4 Total deformation cloud diagram of column

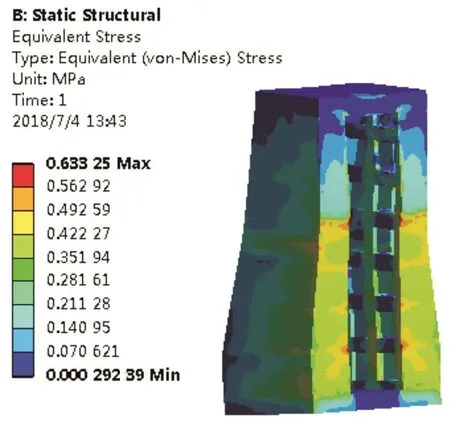
图5 立柱总应力云图Fig.5 Total stress cloud diagram of column

由ANSYS Workbench所得的结果看出，立柱最大等效应力为0.637 4 MPa，符合材料许用应力范围；最大等效应变是3.234 8×10-6mm。根据应力和应变云图，得出立柱在X负方向和Y正方向发生弯曲。

通过云图图4和图5可以看出，数控机床立柱总变形为0.003 86 mm，立柱受到切削力的影响，切削力通过主轴箱传递到立柱，将立柱底座的安装面作为支撑面，立柱同时也受重力影响。立柱底面变形最大，并沿着Y轴正方向逐渐减小，在Z轴发生挤压变形。综上所述，立柱应力在许用范围内，分布均匀，无应力集中现象。

1.2.3 模态分析 模态分析对于研究计算机械产品的固有频率和振型有重要作用，机械产品的动态特性主要由低阶模态决定［12］。因此只研究数控机床立柱前六阶的固有频率和振型。分析结果如图6所示。

通过对图6的分析，发现立柱1、2阶为摆动，3～6阶出现凸振及扭动，具体说明见表2。这说明立柱的壁厚对立柱动刚度影响较大，为提高立柱的动态特性，选择立柱壁厚作为设计参数进行优化。

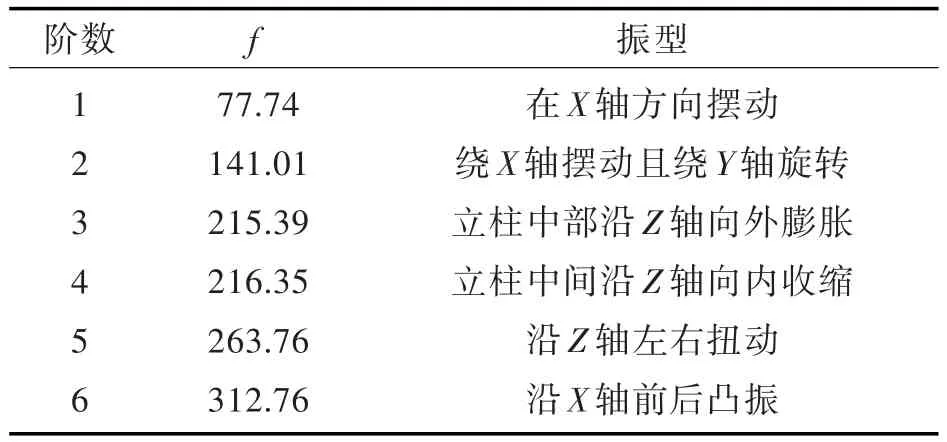
表2 立柱振型及固有频率Tab.2 Natural frequency and vibration mode of column Hz

2 立柱结构优化

灵敏度分析是指结构目标性能函数的变化对结构设计参数变化的敏感程度［13］。首先以基于灵敏度分析选择对立柱动刚度影响最大的参数为设计变量，而后基于响应面法对立柱进行动态优化设计，优化目标是立柱的一阶频率。

2.1 立柱一阶模态灵敏度分析

图6 立柱前六阶模态频率：（a）一阶，（b）二阶，（c）三阶，（d）四阶，（e）五阶，（f）六阶Fig.6 The first six modal frequencies of column：（a）first-order，（b）second-order，（c）third-order，（d）fourth-order，（e）fifth-order，（f）sixth-order

首先通过对设计变量在当前值附近进行扰动，考虑到扰动量相对设计变量当前值均较小，因而对每个设计变量引起目标值的变化采用最小二乘法进行线性拟合，而后基于几何结果计算设计变量的灵敏度。

设计变量相对扰动值N与一阶频率f的关系如图7所示，其中·表示扰动后一阶频率取值。

立柱一阶模态频率与壁厚的变化关系：

式（2）中，u 为未知量，X1，X2，…，X10为设计变量。计算得出立柱尺寸厚度对一阶模态频率的灵敏度，如表3所示。

由表3数据可以看出，尺寸变化对于立柱一阶模态频率灵敏度最大的为内侧壁厚 X10，最小的为第三层肋板厚度 X3。立柱各个尺寸灵敏度大小排列如下：

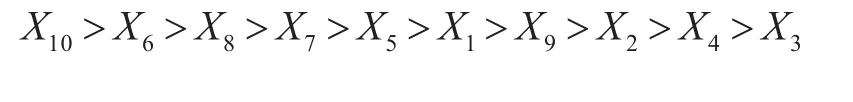
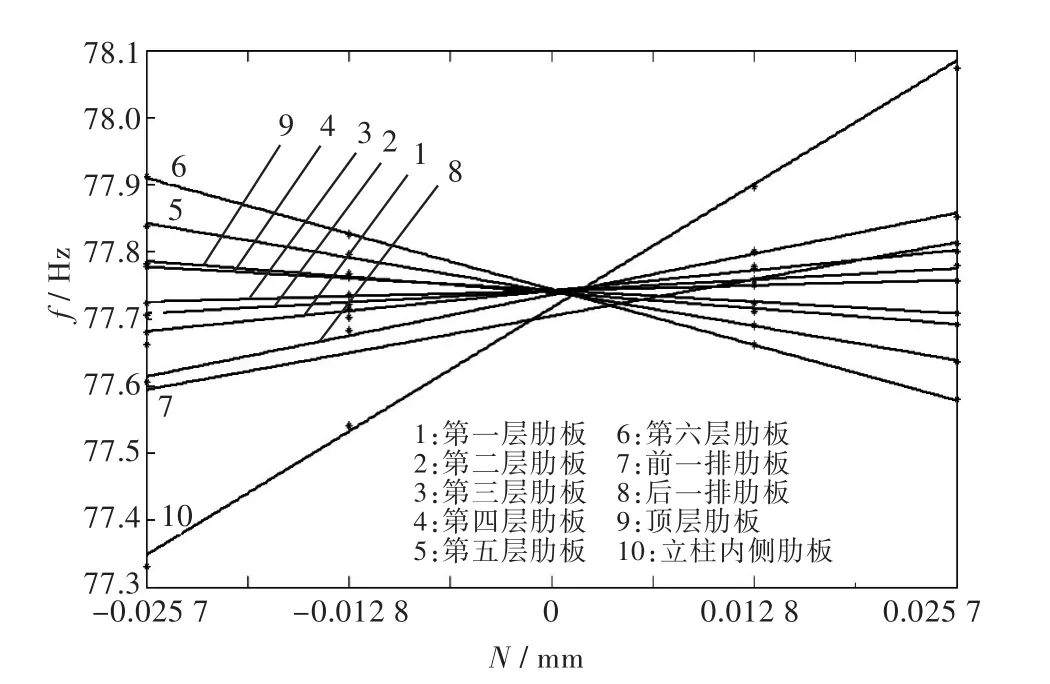
图7 设计变量相对扰动值与一阶频率的关系Fig.7 Relative perturbation values of design variables and first-order frequency

2.2 立柱优化设计

由于立柱的一阶频率相对设计变量无明确解析表达，因而采用处理黑箱模型常用的响应面法对立柱进行优化。响应面法作为一个渐进近似的优化方法，可以很好的解决非光滑非线性的优化问题［14］。其思想是：通过构造一个多项式（具有明确的表达方式）来表达隐式函数，其本质是一种数学统计方法，可对目标函数受多个变量影响的问题进行近似的建模与计算，得到目标函数的优化响应值［15］。

具体优化过程如图8所示。

表3 设计变量变化对一阶模态频率的灵敏度Tab.3 Sensitivity changes of design variables to first-order modal frequencies Hz/mm

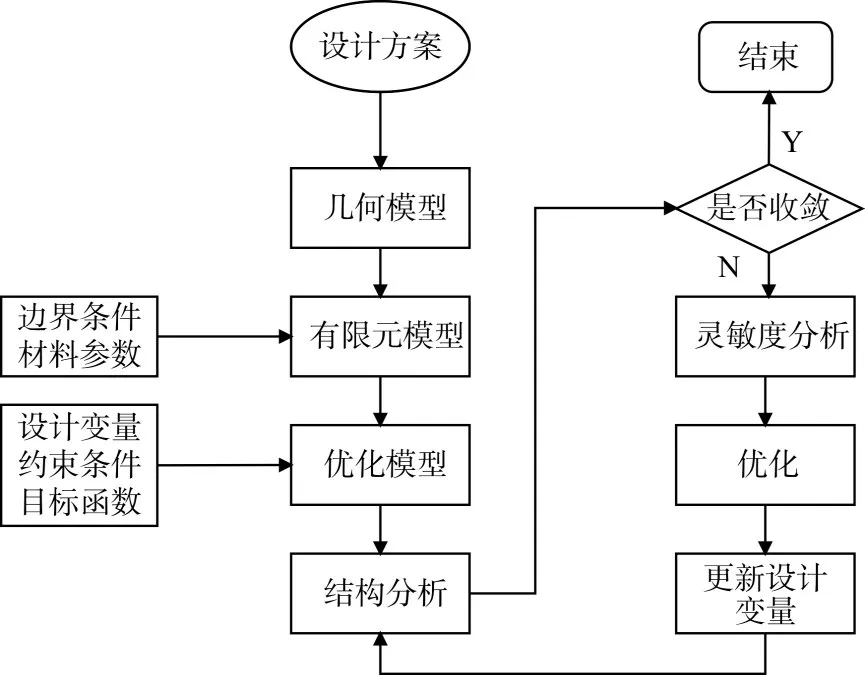
图8 基于有限元分析的优化过程Fig.8 Optimization process based on finite element analysis

据表3数据，对立柱一阶模态频率灵敏度最高的尺寸为内侧侧壁厚X10第六层肋板厚度X6。故选择灵敏度最高的内侧壁厚和第六层肋板厚度作为设计变量。由表1静力学分析得，立柱的最大位移为0.003 86 mm，最大应力为0.634 7 MPa。

因而，优化模型确定为：

设计变量：立柱内侧壁厚 X10，立柱第六层肋板X6。

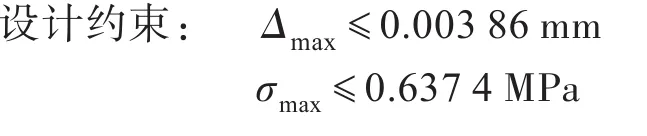
质量减少或者增加量不大（不超过2%）。

优化目标：使立柱动态性能最优（暨一阶模态频率尽可能高）。

上述优化模型可以使立柱在最大位移Δmax不超过0.003 86 mm，最大应力σmax不超过0.637 4 MPa，质量减少或者增加量不大（不超过2%）的约束下，通过优化立柱内侧壁厚X10、立柱第六层肋板X6，使立柱的一阶模态频率尽可能高。

采用ANSYS中响应面优化方法进行计算。得到结果如图9所示。其中，x轴为立柱内侧肋板厚度（mm），y轴为立柱第六层肋板厚度（mm），图9（a）的z轴为立柱一阶模态频率（Hz），图9（b）的z轴为立柱最大位移（10-3mm），图9（c）的z轴为立柱最大应力（MPa）。

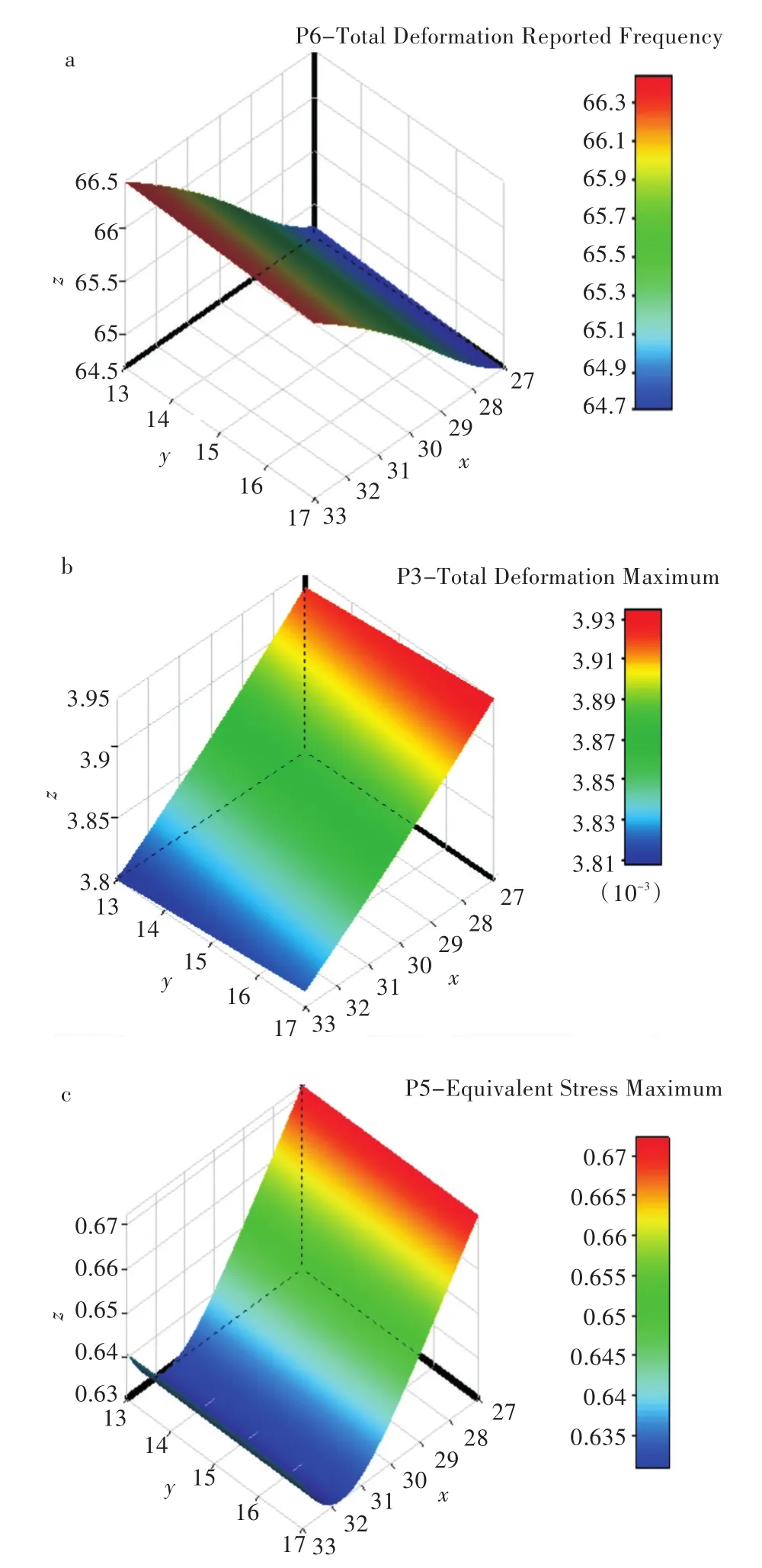
图9 响应曲面：（a）设计变量与一阶模态频率，（b）设计变量与最大位移，（c）设计变量与最大应力Fig.9 Response surface：（a）design variables and first-order modal frequencies，（b）design variables and maximum displacement，（c）design variables and maximum stress

由图9看出，随着立柱内侧壁厚和第六层肋板厚度的增加，立柱一阶模态频率先增加后减少，最大位移减少，最大应力先减少后增加。

在Design Exploration模块下对立柱进行响应面优化，系统寻找到符合优化目标的三个推荐点，如表4所示。

由表4得，第1点的一阶频率提高了1.657 Hz，最大应力和最大位移均符合优化约束，质量仅增加1.6%。优化后的数控机床立柱，一阶频率提高，动态性能得到加强，并且最大位移与最大应力均满足设计要求。

表4 优化结果Tab.4 Optimized results

3 结 语

以数控机床立柱为研究对象，以结构动力学理论为基础，对数控机床立柱结构性能进行分析，并以质量为目标对立柱进行尺寸优化设计。在保证立柱质量不增加过多的前提下，有效提高了立柱的一阶频率，优化了立柱的动态性能。

运用灵敏度分析方法，对立柱尺寸进行分析，得到尺寸变化对于立柱一阶模态频率灵敏度值，选取立柱内侧壁厚及第六层肋板厚度为设计变量，运用响应面法，在ANSYS Workbench中，通过Design Exploration实现立柱优化设计。

得到的设计结果，经过验证，立柱一阶频率提高了1.657 Hz，最大应力和最大位移均符合优化约束，质量仅增加1.6%。优化后的数控机床立柱，一阶频率提高，动态性能得到加强，并且最大位移与最大应力均满足设计要求。

在今后的工作中，首先进行立柱拓扑优化，找到更加合理的初始方案，然后对立柱进行参数优化，使得在立柱一阶频率提高的同时，质量减轻，得到更加合理的设计方案。