基于智能组合算法风电场调度功率预报设计

朱建红，黄 琼，孟棒棒

(南通大学 电气工程学院，江苏 南通 226019)

0 引 言

风力发电机组发出功率时刻处于波动状态，这种出力特性使得发电机组并网稳定运行面临着巨大挑战[1]。为规范电网调度和风电场功率预测，国家能源局发布了风电功率预测系统功能规范[2]，对风电功率准确预报要求进行了严格量化。同时为保证风电场并网安全稳定运行，电网公司颁布了《风电场接入电力系统技术规定》，规定了风电场输出并网波动率控制要求。

作为新预测方法，组合预报成为发展趋势[3]，其核心思想是消除大预报偏差以降低独立预测误差带来的风险，将不同统计预测值加权平均，例如SVM预测与最小二乘法、混合遗传算法[4,5]。现有成果显示，风电预测平均绝对误差(MAE)可以控制在总装机容量10%～15%以内[6]。相比德国的WPMS，采用人工智能神经网络方法，预测均方根误差(RMSE)在7%～19%。由欧盟资助开发的ANEMOS项目，预测误差在10%左右。国内较早的预测系统是由电力科学研究院开发的物理混合预测模型[7]。在平抑风电场功率输出波动方面，许多学者和科研人员也进行了深入研究[8]。控制策略主要分为加储能和不加储能装置[9]。加储能装置平抑功率波动方法有加超级电容、新型电池、新型飞轮装置和超导磁[10]，成本较高。不加储能的基于算法设计功率平滑处理的方法有低通滤波器法、滑动平均法、小波包分解等。课题预报策略基于智能预测算法研究，包括应用较广的BP神经网络法，波形追踪能力较强的小波分析函数与神经网络相结合的小波神经网络法和基于最小二乘法的支持向量机法(LS-SVM)。预测结果利用小波包平滑,通过误差及平滑对比分析，确定较优预报策略。

1 风电功率平滑及预报指标分析

1.1 预测误差

按规定，超短期功率预测时间点间隔设定为15 min预测一次，预测程序单次运算时间应少于5 min。风电场短期预测月均方根误差应小于20%，超短期预测第4 h预测值月均方根误差应小于15%。误差统计指标至少应包括均方根误差、平均绝对误差、相关性系数、最大预测误差。求取如式(1)～式(4)。

均方根误差(RMSE)

(1)

平均绝对误差(MAE)

(2)

相关性系数(r)

(3)

最大预测误差(δmax)

δmax=max(|PMi-PPi|)

(4)

1.2 波动率

风电场波动包括l min功率变化率和10 min功率变化率，具体推荐值参照表1。

表1 风电场功率波动推荐值

2 功率预报方案设计

预报功率曲线的生成采取先预测，再进行波动率分析并进行功率平滑的方法，将风电场功率平滑后的功率曲线作为最后的预报结果。

2.1 风电场功率输出预测技术

研究与仿真数据均来自河北某一风电场，装机容量在30 MW～150 MW之间，由于预测功率和实际功率的采样周期为15 min，只能进行功率波动相对计算。

2.1.1 BP神经网络法在风电场功率预测应用

matlab调用train函数训练网络，样本数据共2880个，记录该风场一个月运行情况，实际风速和实际功率作为网络测试样本，并选用前1000个数据作为训练样本，后面1880个点作为测试数据。图1为0 min到15 000 min实际和预测风电场功率，拟合度较好。从15 000 min到40 000 min为滚动预测风电场功率和实际功率，误差较大，但基本趋势正确。

图1 实际风电场功率和预测风电功率对比

将运算数据保存，根据式(1)～式(3)，结果如下：RMSE=0.142，RMSE<0.15，MAE=0.114，r=0.9212，均方根误差小于15%，符合标准要求[2]。

2.1.2 小波分解法在风电场功率预测中的应用

小波神经网络mallat运行结果如图2所示。样本数据前1000个点作为训练样本，任取第1000至2000个时间点风速作为输入参数，将预测功率与这1000个时间点实际风电场功率进行对比。小波神经网络预测结果与实际风电场功率非常相近。

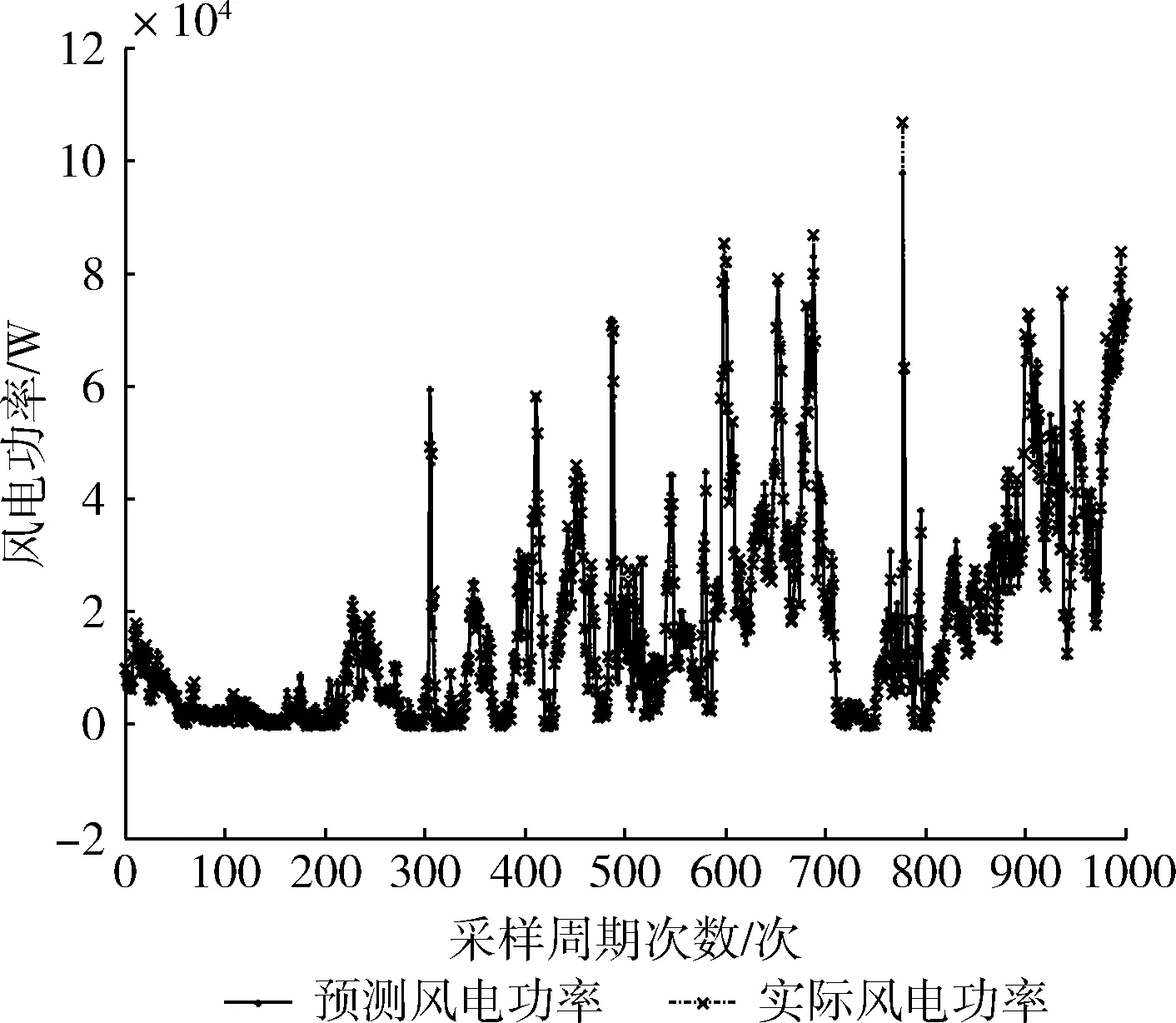
图2 小波神经网络预测结果

小波神经网络隐含节点的权值见表2。表中Wij为风电场功率曲线6个隐含节点权值参数，Wjk为风速曲线隐含节点权值参数。i是样本训练迭代次数，共计2880；j为隐含层节点个数，j=6；k为输入节点个数，k=1。将预测后各个时间点风电功率保存下来，根据式(1)～式(3)分别进行均方根误差RMSE、平均绝对误差MAE和相关性系数r计算。RMSE=0.0785，RMSE<0.15，MAE=0.0554，r=0.9757,均方根误差小于15%，预测结果完全符合要求。

2.1.3 支持向量机在风电场功率预测中应用

支持向量机在风电场功率预测方面应用就是根据回归机功能特性，对样本采样点进行数据统计，这仅考虑风速对输出功率的影响，以风速和风电场功率为xy轴构成二维平面样本点进行最优曲线拟合，从而找到风速与风电场功率的映射关系。以一个月内2880个采样点作为测试数据，将得到的风电场功率预测曲线与当月实际风电场功率曲线对比，结果如图3所示。实际功率曲线与预测功率曲线基本吻合，根据式(1)～式(3)误差计算。RMSE=0.0964，RMSE<0.15，MAE=0.0661，r=0.9650。

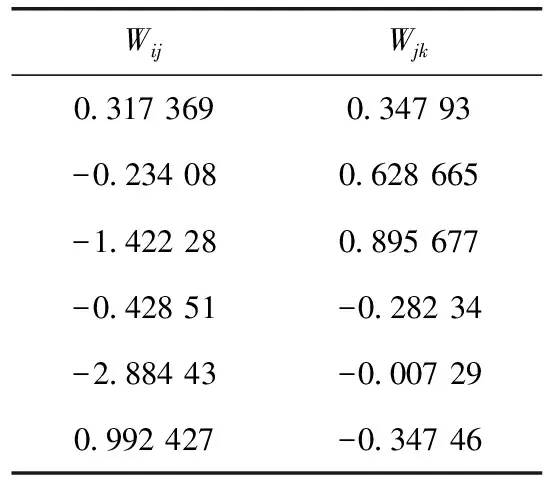
表2 小波神经网络权值参数

由于只考虑风速对风电场功率的影响而忽略其它气象参数，也是风电场功率预测误差主要因素。

2.1.4 预测仿真比较分析

风电场同一个月内的历史数据进行实例分析，3种方法预测的均方根误差、平均绝对误差和相关性系数(即预测准确度)的计算。结果见表3。

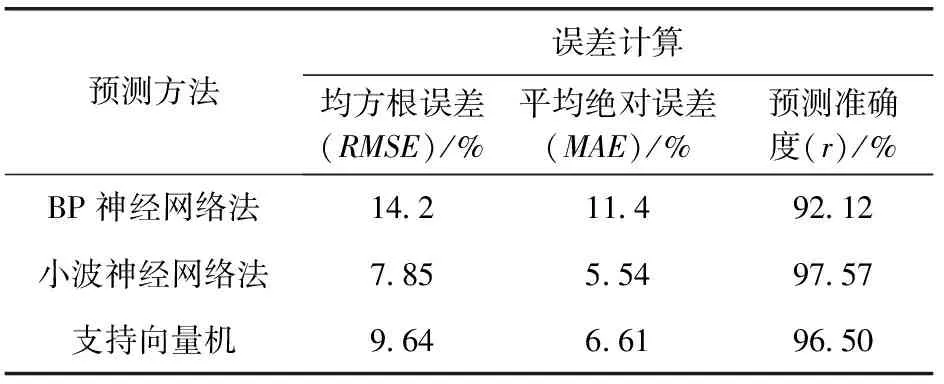
表3 3种方法预测结果误差对比

3种预测方案误差对比得出以下结论：

(1)BP神经网络法预测的准确度较低(即相关性系数最低)，预测的均方根误差和平均绝对误差都比小波神经网络和支持向量机高。主要原因在于BP神经网络对训练样本要求比较高，需要可信度及完整性高的训练样本。

(2)小波神经网络的预测准确度0.9957，预测功率的均方根误差和平均绝对误差也是最低的，可见小波分析函数和神经网络的结合挖掘数据之间细微关系能力较大，较强学习能力可寻找风速曲线和功率曲线中波形细节信号和轮廓信号之间映射关系，预测误差较小。

(3)支持向量机处理多维复杂数据优势使其成为当前功率预测较为热门研究之一，但因忽略其它功率输出影响因素，仅实现二维最优曲线回归，课题测试没有突出这一特点。实例检验后发现误差比小波神经网络稍大，准确度0.9950。

总的来说，表3可看出3种预测结果均方根误差都小于15%，满足国家标准。其中小波分解法和支持向量机预测结果较好。

2.2 风电场功率平滑算法设计

小波包分解对预测的风电场功率进行平滑，将频带进行多层次划分，对小波分析没有细分的高频部分进一步分解，并根据需要分析信号特征，自适应选择相应频带，使之与信号频谱相匹配，从而提高高频区分辨率。课题从平滑前后的功率曲线波动分析，检验功率曲线平滑效果，给出平滑前后功率修正分析(实际控制中结合实际功率进一步修正)。风电场功率波动量表达式如式(5)所示

ΔP=PWG(k)-Pout(k-1)

(5)

式中：PWG(k)为k时刻风电功率，Pout(k-1)为k-1时刻风电场输出功率，则k时刻风电场功率波动率γ如式(6)所示

γ=ΔP/Cap

(6)

式中：Cap为装机容量，通过平滑功率曲线控制波动率γ在0.2以内。

2.2.1 先BP神经网络预测后小波包平抑

(1)波动分析

BP神经网络的预测功率曲线未平滑前的波动率如图4所示。

图4 BP功率预测曲线各点波动率

图中波动率γ大于0.2的点共有94个，占样本总和3.26%；波动率γ大于0.1的点共有352个，占样本总和12.22%。功率平滑进行小波包分解平滑后的功率曲线与未平滑对比如图5所示。平滑后功率曲线波动率γ大于0.2的点共29个，占样本总数1.01%；波动率γ大于0.1的点共有73个，占样本总数的2.53%。

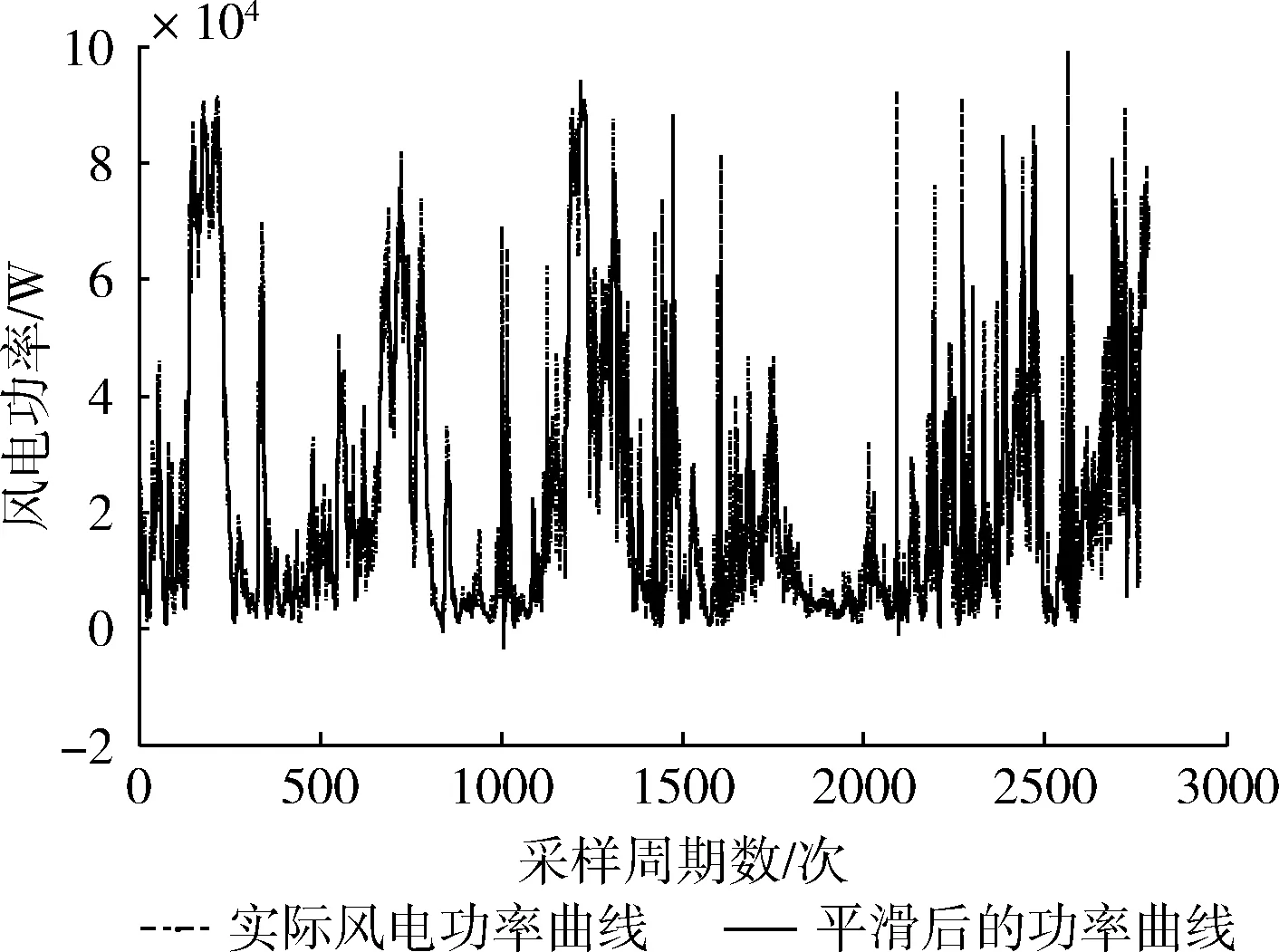
图5 平滑前后的功率曲线对比

(2)功率修正量

平滑前后功率修正量计算作为电网调度决策参考。数据统计分析按修正量区间划分。如表4所示，功率修正量在5 KW以内的采样点占样本总容量73.5%，在区间[5 KW,10 KW]内的修正功率占20%，大多数功率修正值比较小，但超过10 KW只占总体容量6.5%，修正难度较大。由此可见，BP神经网络预测后平滑难度较大，效果总体尚可。

2.2.2 先小波分解预测后小波包波动平抑

(1)波动分析

图6中，数据统计波动率γ大于0.2的点共有12个，占样本总和1.20%；波动率大于0.1的点共有50个，占样本总和5%。

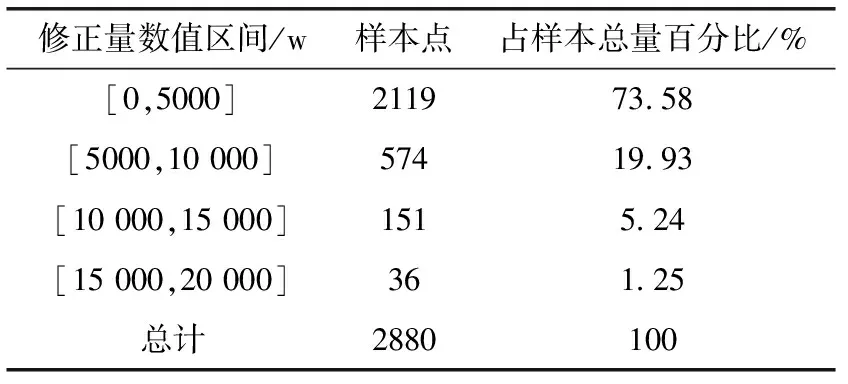
表4 BP神经网络算法功率修正区间分布

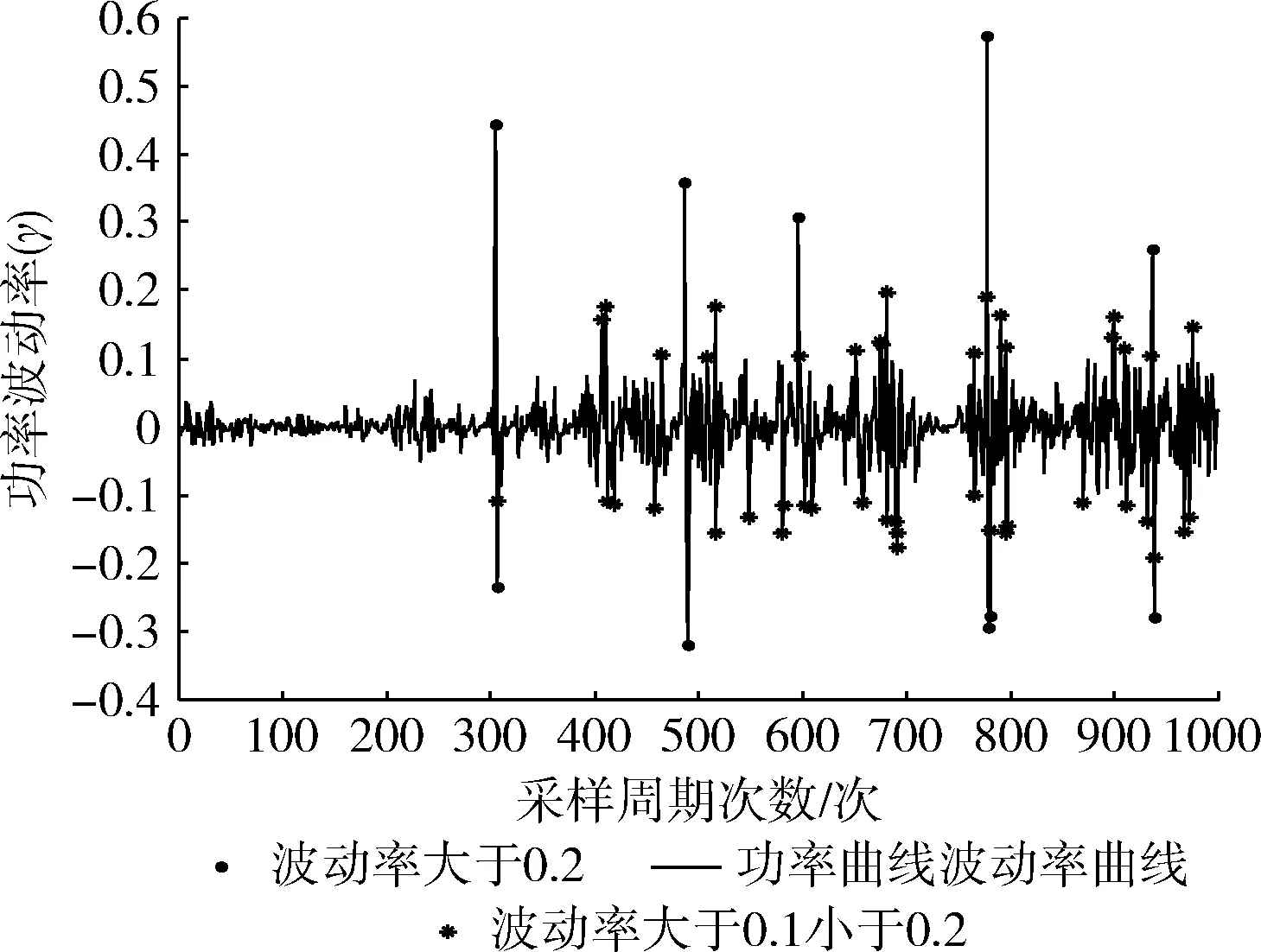
图6 小波功率曲线波动率

平滑前后功率曲线平滑对比如图7所示。虚线代表平滑前功率曲线，粗实线代表平滑后功率曲线。平滑后的曲线经数据统计，波动率γ大于0.2的点共有7个，占样本总数的0.7%；波动率γ大于0.1的点共有23个，占样本总数的2.3%。

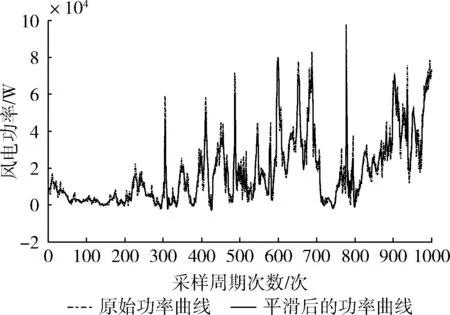
图7 平滑前后的小波神经网络预测曲线

(2)功率修正量

预测功率曲线平滑前后数据统计分析修正量区间划分见表5。

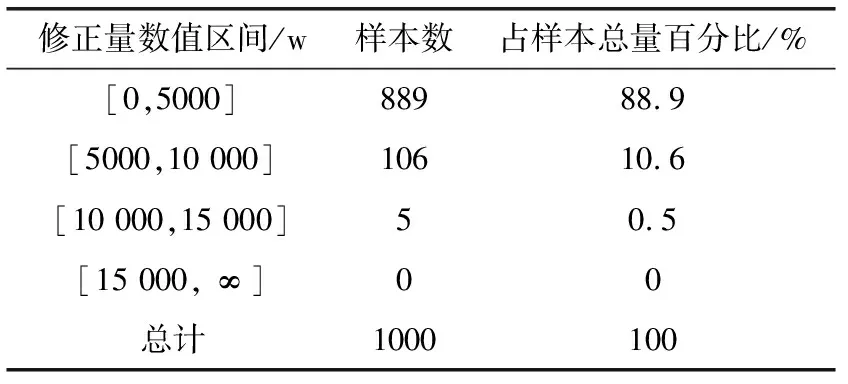
表5 小波神经网络功率修正区间分布

由表5可知，修正功率在5 KW以内的采样点占样本总容量89%，在区间[5 KW,10 KW]内的修正功率占10%，绝大多数功率修正值比较小，符合风电场实际作业需求，总体平滑效果较好。

2.2.3 先支持向量机预测后小波包波动平抑

(1)波动分析

支持向量机预测功率曲线波动率如图8所示。经数据统计波动率γ大于0.2的点共有17个，占样本总和0.61%；波动率γ大于0.1的点共有110个，占样本总和3.95%。

图8 SVM预测风电场功率曲线波动率

平滑前后风电功率曲线如图9所示。平滑后功率曲线经数据统计波动率γ大于0.2的点共有6个，占样本总数的0.22%；波动率γ大于0.1的点共有24个，占样本总数0.86%。

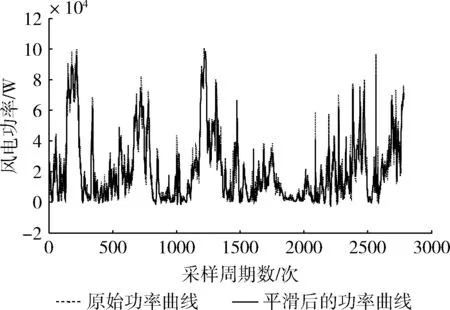
图9 平滑前后风电场对比曲线

(2)功率修正量

平滑前后所需修正的功率数据统计按修正量区间划分见表6。

由表6可知，修正功率在5 KW内的采样点占样本总容量85%，区间[5 KW,10 KW]内的修正功率占14%，绝大多数功率修正值比较小，便于风电场实行，修正之后的功率曲线波动率也大幅下降，总体上平滑效果良好。

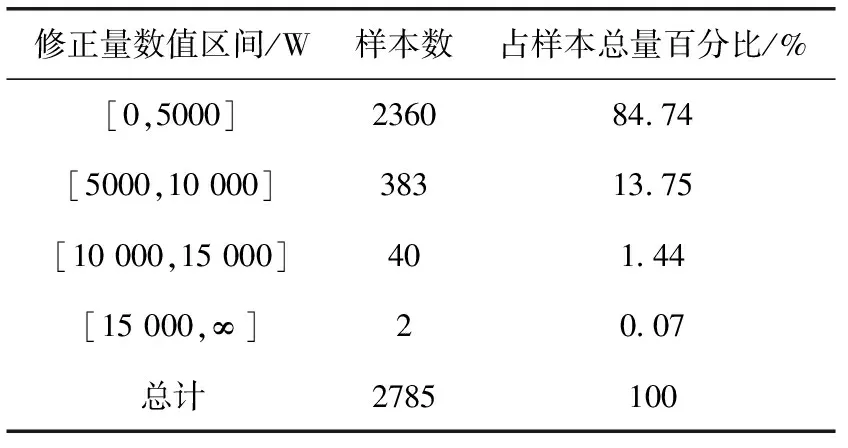
表6 支持向量机功率平滑修正量区间

3 总体仿真结果比较分析

3种先功率预测后波动平抑见表7。

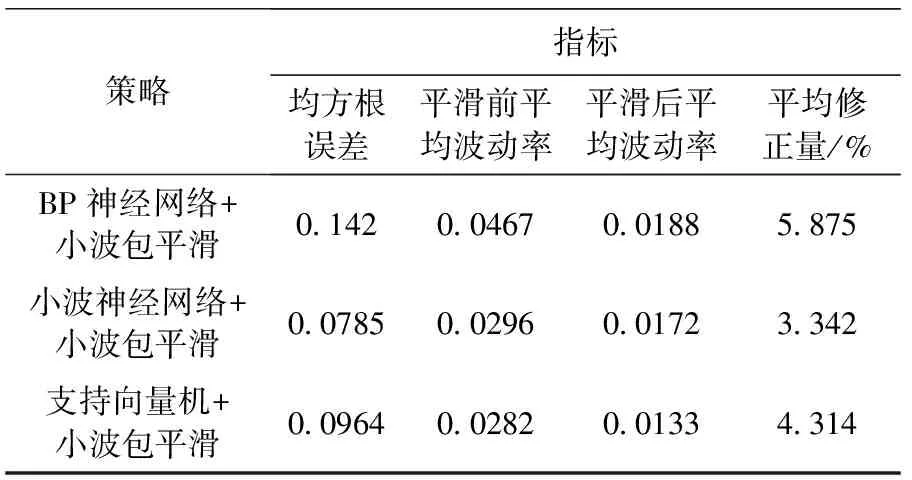
表7 3种方法预测误差及小波包平滑波动率

分析可以看出，小波神经网络的预测兼平滑总体效果比其它两者好。但运行也发现小波神经网络计算速度是3种方法中最慢的，因小波分解函数将风速和功率都分解成6个部分，平均计算一次需要耗时1.125 s(国家标准内)，运行时占用内存也是最高的，计算的工作量近似于BP和SVM的6倍。

4 结束语

风电场功率输出波动率太大不利于电网稳定运行，影响整体电网的电能质量，预报不准不利于电网调度计划的制定与执行。并网功率平滑且预报准确是风电场功率预报的追求目标。现有文献的研究成果大多针对其中之一展开，本文在综合考虑两者基础上针对风力发电中的功率预测和风电场功率平滑问题，分别采用BP神经网络、小波分解神经网络和支持向量机进行风电场功率预测，并以河北某电厂一个月内的数据作为实例检验分析。选用小波包分解方法对前3种方法预测的功率曲线进行平滑。给出曲线的波动率和平滑前后的功率修正量，得出先小波神经网络法后小波包分解平滑兼准确预报的较优方案。

风电场预测结果客观上高度依赖气象预报的准确度，所以预测误差相对较大。功率平滑技术要求电网具备较高调节能力，尽量避免弃风限电事件发生。随着储能技术的发展，就地平抑风电功率波动问题也将缓解电网这方面的调节压力。