基于全局和局部回归的因果定向改进算法
潘孟姣 蔡青松
(北京工商大学计算机与信息工程学院 北京 100048)
0 引 言
因果关系[1]是普遍存在于事物间的联系,它从本质上描述了何种原因直接、间接或较大程度上导致了某种结果,因此比相关关系[2]对某种现象的发生具有更好的解释性[3]。然而在实际中,鉴于工具的缺乏及耗费的代价过大等因素,人们通常只能依据有限的观测数据和经验知识来分析并推断事物产生的根源,其结果往往具有明显的局限性及不确定性。近年来基于人工智能的数据分析方法得到了快速发展,进而推动了因果关系推断领域在理论和实践上的进步。自20世纪80年代以来,基于观测数据的因果关系推断获得了显著的研究成果,大量文献表明[4-7],对已获取的数据进行因果关系推断是一个基础科学问题,在诸多领域均有着潜在的重要应用价值。例如,在医学诊断领域,基于就诊者的各项检查数据进行因果分析,有利于对其健康状况做出准确的判定,对指导后续行为具有重要意义。
采用传统的因果网络结构学习方法[8-9]可以识别观测数据间的部分因果关系,但此类方法大多无法对马尔科夫等价类[10]进行准确地判断,即无法对变量之间的因果方向进行准确地判定。推断观测数据间的因果方向(也称因果定向[11]),是当前因果关系推断领域的重要研究热点之一。
近年来,针对观测数据间一对一因果关系的定向问题,学者们提出了多种方法[12-16]。其中,加性噪声模型ANM(Additive Noise Model)[12,17]是解决这类问题的初步尝试,它假定结果变量由原因变量及与原因无关的加性噪声决定,然后通过检验所假设的原因变量与加性噪声之间的独立性来进行因果定向。在这种强假设下提出的方法在特定仿真数据上表现出高准确率,但实际中将会存在两个方向都符合或都不符合假设的情况,使其在真实数据集上的准确率受限[12,16]。一些基于独立性假设[10]的研究工作也采用独立性测试进行因果定向,如DC算法[13]。根据独立性假设,如果变量X和变量Y间的因果方向为X→Y,则边缘分布P(X)和条件分布P(Y|X)是相互独立的,反之则不独立。DC算法在多元分类数据上计算P(X)和P(Y|X)之间以及P(Y)和P(X|Y)之间的距离相关系数,将具有较小相关性的方向推断为可能的因果方向,此算法仅适用于多分类数据。
除采用独立性测试进行因果定向外,另一类方法则主要采用柯氏复杂度作为基础。算法的马尔科夫条件指出,两个随机变量X和Y之间具有最低柯氏复杂度的方向是最有可能的因果方向[10]。但由于停机问题(即一个程序是否能在有限的时间之内结束运行),柯氏复杂度无法计算。ORIGO算法[14]采用最小描述长度MDL原理[18]来估计柯氏复杂度。该算法建立在基于MDL原理的PACK算法[19]上,并使用决策树来编码布尔型数据,通过近似计算柯氏复杂度来推断因果方向,适用于二分类数据。CISC算法[15]将数据视为服从多项分布的随机变量,通过改变参数产生不同的分布,用于构建概率分布的模型类。此算法通过使用随机复杂度来估计柯氏复杂度,进而推断因果方向,适用于多分类数据。该随机复杂度是数据相对于对应模型类的最小描述长度。
文献[16]遵循基于柯氏复杂度的信息理论方法,通过构建回归模型,采用MDL原理估计两个变量相互回归所需柯氏复杂度的大小,以此判定两者间可能的因果方向,并实例化为SLOPE算法。相对于其他类型的算法,该算法在分类、线性及非线性数据上都具有较高的推断准确率。鉴于实际中遇到的不仅仅是分类问题,两个变量间可能存在线性或更复杂的非线性关系。因此相对于其他算法,其更适用于观测数据的因果定向。但此算法在遍历回归模型计算对应描述长度时需消耗大量时间成本,影响算法效率。
因此,本文针对这个问题,对原始的因果定向算法进行改进,提出一种基于全局和局部回归的因果定向改进算法ISLOPE(Improved SLOPE)。该方法尝试根据模型的特征分别构建全局和局部回归模型。与原模型相比,减少了部分不符合对应特征的冗余模型,降低了遍历回归模型计算对应描述长度时所需的时间成本,进而提高了原算法的效率。实验结果表明,相较于其他对比算法,所提出的算法在合成数据及真实观测数据上都具有较好的性能。
1 理论基础
因果定向算法的目的是判定两个变量间因果关系的方向,即在两者中推断并区分原因变量和结果变量。采用基于柯氏复杂度的方法进行因果方向判定是因果定向研究的主要方法之一。
1.1 柯氏复杂度
字符串s的柯氏复杂度K(s)是通用图灵机U产生s并停机的最短二进制程序p*的长度,记为K(s)=|p*|。y相对于x的条件柯氏复杂度K(y|x)是当x作为程序的输入被提供时产生y并停机的最短二进制程序p*的长度[20]。概率分布P的柯氏复杂度是在U上输入x和精度ε后产生符合精度的P(x)然后停机的最短二进制程序p*的长度,条件概率分布的柯氏复杂度定义类似。
下面使用柯氏复杂度进行因果推断。虽然此推理规则的理论基础坚固,但由于停机问题,柯氏复杂度不可计算。
定理1(柯氏复杂度因果推断[21]) 若变量X和Y间的因果方向为X→Y,则有:
K(P(X))+K(P(Y|X))≤K(P(Y))+K(P(X|Y))
(1)
1.2 MDL原理
MDL原理为柯氏复杂度的近似计算提供了合理的手段,它规避了柯氏复杂度的可计算性问题,将程序限制在可终止的且足以捕捉大部分规则的程序上。在MDL理论中,程序通常被称为模型。使用模型m∈M编码数据X时,X总的描述长度为模型m的长度加上编码后长度[18],即:
L(X,m)=L(m)+L(X|m)
(2)
MDL原理表明,给定数据X和模型类M,最佳的统计模型mo∈M将为数据X产生最小的描述长度。
1.3 加性噪声模型
定义1(加性噪声模型[17]) 假设变量X和变量Y满足以下条件,则称X到Y符合ANM。
Y=f(X)+NN⊥X
(3)
式中:f是任意函数,N是独立于X的加性噪声。
对于变量X和Y,当X到Y符合一个ANM,但Y到X不符合时,称X是Y的原因,Y是X的结果,即因果方向为X→Y。
2 因果定向方法及改进算法
2.1 模型及指标构建
回归模型类M由多个子模型类Ms构成。每个Ms对应一个线性或非线性函数,单个模型类Ms由多个不同参数的子模型m构成。单个子模型m的描述长度定义如下:
(4)
将回归模型的参数类Υ中的每一个参数γ编码到一定的精度ε,用最小的整数δ来设定参数γ,使其满足γ×10δ≥10ε。用Lo表示整数z(z≥1)的MDL最优编码[22],如式中的Lo(δ)表示整数δ的MDL最优编码。
已知两组相关的数据变量X={x1,x2,…,xn}和Y={y1,y2,…,yn},假设没有混杂变量[23]的影响,即X和Y没有隐藏的共同原因Z。使用子模型m∈M将变量X向变量Y回归,并将它产生的误差视为服从高斯分布的噪声。根据MDL原理在回归模型类M中选出X向Y回归的最优子模型mo。由加性噪声模型Y=f(X)+N可知,一个出现多次的值将对应一系列服从N同类型分布的Y值。
变量X和变量Y之间的整体关系使用全局模型mo来拟合,而对于一个x值匹配多个Y值的情形(附加数据),增加局部模型类Ma来拟合。具体而言,对于对应多个Y值的xi,将其变换为服从均匀分布的序列:
Xi={-v,…,v} |Xi|=|Yi|,v∈N*
(5)
式中:Yi为映射到xi上的Y值升序排列后的序列,N*为正整数。
原始的因果定向算法在模型类M中选出Xi向Yi回归的最优子模型ma。由于其全局和局部回归模型统一构建,故而模型类M中的所有子模型既都属于全局回归模型又都属于局部回归模型。
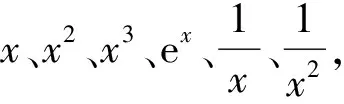
改进后模型类M=mo∪Ma的描述长度由下式给出:
L(M)=Lo(|M|)+lb((|Ma|-1)⟹(|X|-1))+
(6)
即:首先描述所选用的模型的个数,其次将局部模型类Ma映射到与之对应的数据X上(其中⟹表示此映射),然后分别使用lb(|M|)比特、lb(|Ma|)比特标记所选用全局子模型及局部子模型的类型,最后描述所选模型自身。
变量X的描述长度定义如下:
L(X)=-nlbd
(7)
d=min{|xk+1-xk|||xk+1≠xk|,k=1,2,…,n-1}
(8)
式中:d表示X中相邻元素间的最短距离(忽略零值)。
已知M、X的条件下Y的描述长度定义如下:
(9)
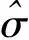
对于数据对(X,Y),X到Y的总描述长度LX→Y定义为X的描述长度、所选用的模型类M的描述长度及已知M、X的条件下Y的描述长度之和,即:
LX→Y=L(X)+L(M)+L(Y|M,X)
(10)
Y到X的总描述长度LY→X的定义类似。
2.2 因果方向推论规则
使用上述描述长度指标,得出以下因果推论规则。
(1) 如果LX→Y (2) 如果LX→Y>LY→X,则推断出因果方向为Y→X。 (3) 如果LX→Y=LY→X,则无法确定。 也就是说,如果“先描述X,然后给定X再描述Y”较“先描述Y,然后给定Y再描述X”容易,则推断出X很可能是Y的原因;如果反过来,则推断出Y很可能是X的原因;否则无法判断。 算法1改进型因果定向算法ISLOPE 输入:数据对(X,Y); 输出:总描述长度LX→Y。 步骤1由公式计算X的描述长度L(X)。 步骤2初始化模型类M为空,LX→Y=L(X)。 步骤3在回归模型类M中匹配X向Y回归的最优子模型mo,并将其添加到模型类M中,由公式计算并更新此时的LX→Y。 步骤6输出LX→Y。 为验证改进算法ISLOPE的性能,采用合成数据及真实数据进行实验。并使用原始的SLOPE算法[16]进行对比。此外,为更全面地验证该算法的性能,实验部分还分别选择基于柯氏复杂度的CISC算法[15]及基于独立性假设的DC算法[13]进行对比。 所有实验均在运行Linux的内存为4 GB、处理器是Intel®CoreTM2 Quad CPU Q9400 @2.66 GHz×4的计算机上执行。 合成数据是使用加性噪声模型Y=f(X)+N生成的因果方向为X→Y的数据,变量X分别从表1的分布中进行采样,函数f分别从表2的函数中选择,N使用独立生成的均匀分布噪声{-t,…,t},其中t={1,2,…,7}。 表1 数据分布及参数设置 表2 函数及参数设置 对X服从表1中不同分布、f取表2中不同函数的多种组合分别生成100组因果对,每组样本量为500条。在图1中,将ISLOPE算法在不同组合下的推断准确率与原算法SLOPE以及CISC、DC算法作对比。 图1 不同分布不同函数下算法准确率对比 如图1(a)所示,当生成模型遵循文献[15]将结果变量映射为多分类数据时,算法ISLOPE和SLOPE与CISC算法的准确率接近,且两者在所有分布上均优于DC算法。当f为线性函数时,如图1(b)所示,在多种分布类型下ISLOPE和SLOPE均优于CISC和DC。当f为非线性函数时,如图1(c)所示,对比算法CISC及DC已经不再适用,而ISLOPE和SLOPE依旧保持高准确率且准确率略有提升。当f混合使用表2中的五种函数时,如图1(d)所示,ISLOPE和SLOPE均优于CISC和DC。在图1所示的多种组合方式中,改进算法ISLOPE近似保持原算法SLOPE的准确率不变。 对X服从表1中偶数位置的不同分布、f取表2中第二和第三位置的线性及非线性函数的多种组合分别生成样本量为500条的因果对。 在图2中,将ISLOPE算法在不同组合下推断一组数据对所需运行时间与对比算法作比较。DC和CISC算法在多种情形下的运行时间都很低,ISLOPE及SLOPE算法的运行时间为数秒到数十秒不等,且改进算法ISLOPE在每种情形下的运行时间都低于原算法,约为原算法的50%。 图2 不同分布不同函数下算法运行时间对比 设置变量X服从均匀分布,函数取f(X)=aX。在分别生成100对样本量为500i(i=1,2,…,10)条的合成数据集的情况下,将ISLOPE算法在不同样本量下的准确率情况与对比算法作比较,如图3(a)所示,ISLOPE算法的准确率均值约为65%,与SLOPE算法相同,高于其余对比算法。 在分别生成100i(i=1,2,…,10)组样本量为500条的合成数据集的情况下,将本文算法在不同数据对数下的准确率情况与对比算法作比较,如图3(b)所示,ISLOPE算法的准确率均值约为72%,与SLOPE算法相同,高于其余对比算法。从图3中可知,四种算法在不同样本量及不同数据对数下的准确率都比较集中。 图3 不同样本量或不同数据对数下的算法性能对比 真实数据采用95组已知因果方向的来自不同领域的观测数据集[7],每组样本量为几百到几万条不等,这些数据是对因果定向算法进行测试的基准数据。 由图4可知,ISLOPE的准确率与SLOPE算法保持一致,高于其余对比算法,且在全部数据集上的准确率约74%,较CISC算法高出10%。ISLOPE及SLOPE算法在全部数据集上的运行时间如表3所示,改进算法的时间消耗约比原算法降低50%。 图4 真实数据算法准确率对比 表3 真实数据算法运行时间对比 本文从探索和发现蕴含在观测数据间的因果关系这一角度出发,针对一对一因果关系的定向问题进行研究。最近的科研结果表明基于全局和局部回归的SLOPE算法在因果定向问题上表现出较好的性能。但模型冗余使得该算法在效率上存在一定的局限性。本文提出根据模型特征分别构建全局和局部回归模型的方法,该方法可以避免原算法中的冗余模型引起的时间消耗,降低算法的运行时间,进而提高原算法的效率。并在此方法的基础上提出一个改进的因果定向算法ISLOPE。实验部分对改进算法进行性能验证,结果显示,所提出的算法能够在保持原算法准确率近似不变的前提下将运行时间降低一半左右,且该算法的整体性能优于其他两种对比算法。 仅针对一对一因果关系的定向问题进行研究仍然不足,为更深入地挖掘蕴含在观测数据间的因果关系,下一步研究工作将在多变量因果定向问题(如多对一、一对多、多对多)上进行。2.3 算法描述
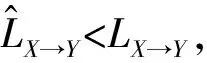
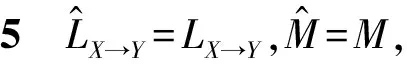
3 实验验证
3.1 合成数据及参数设置


3.2 准确率
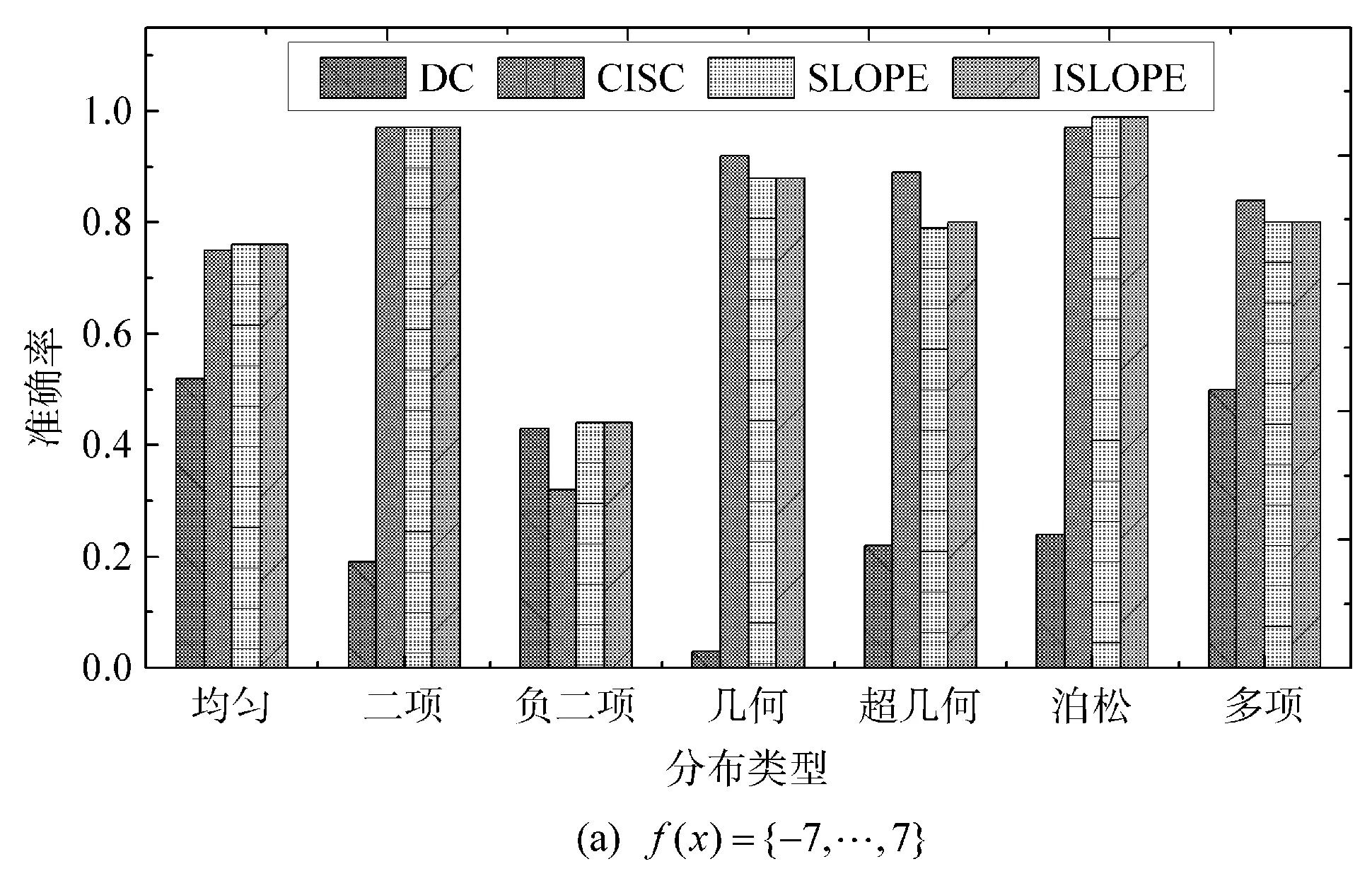
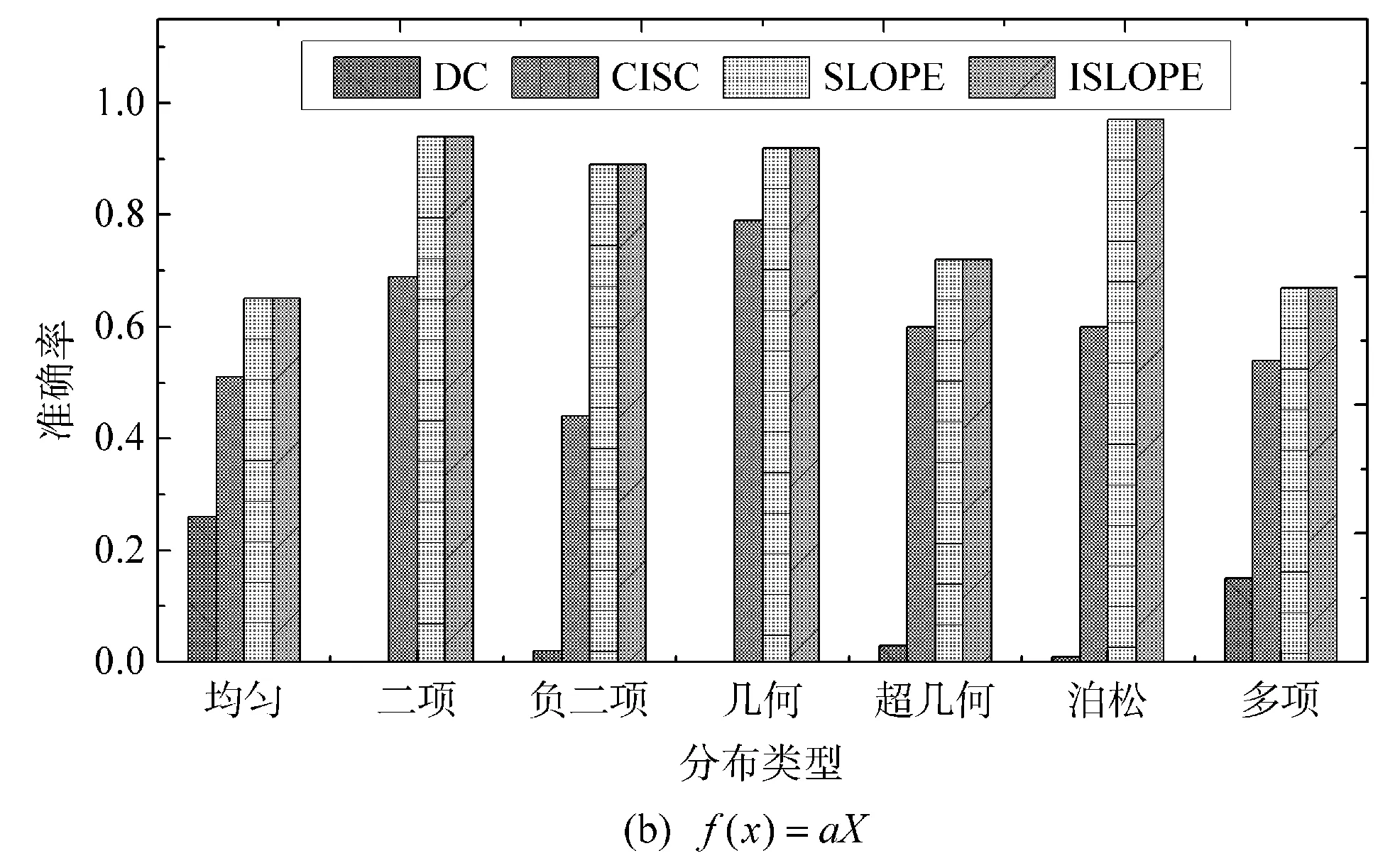

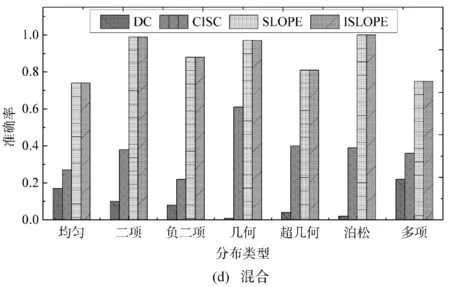
3.3 效 率
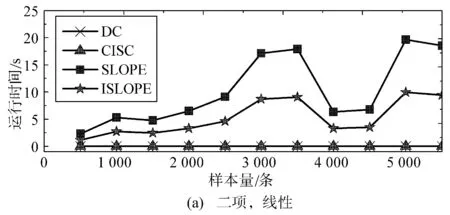
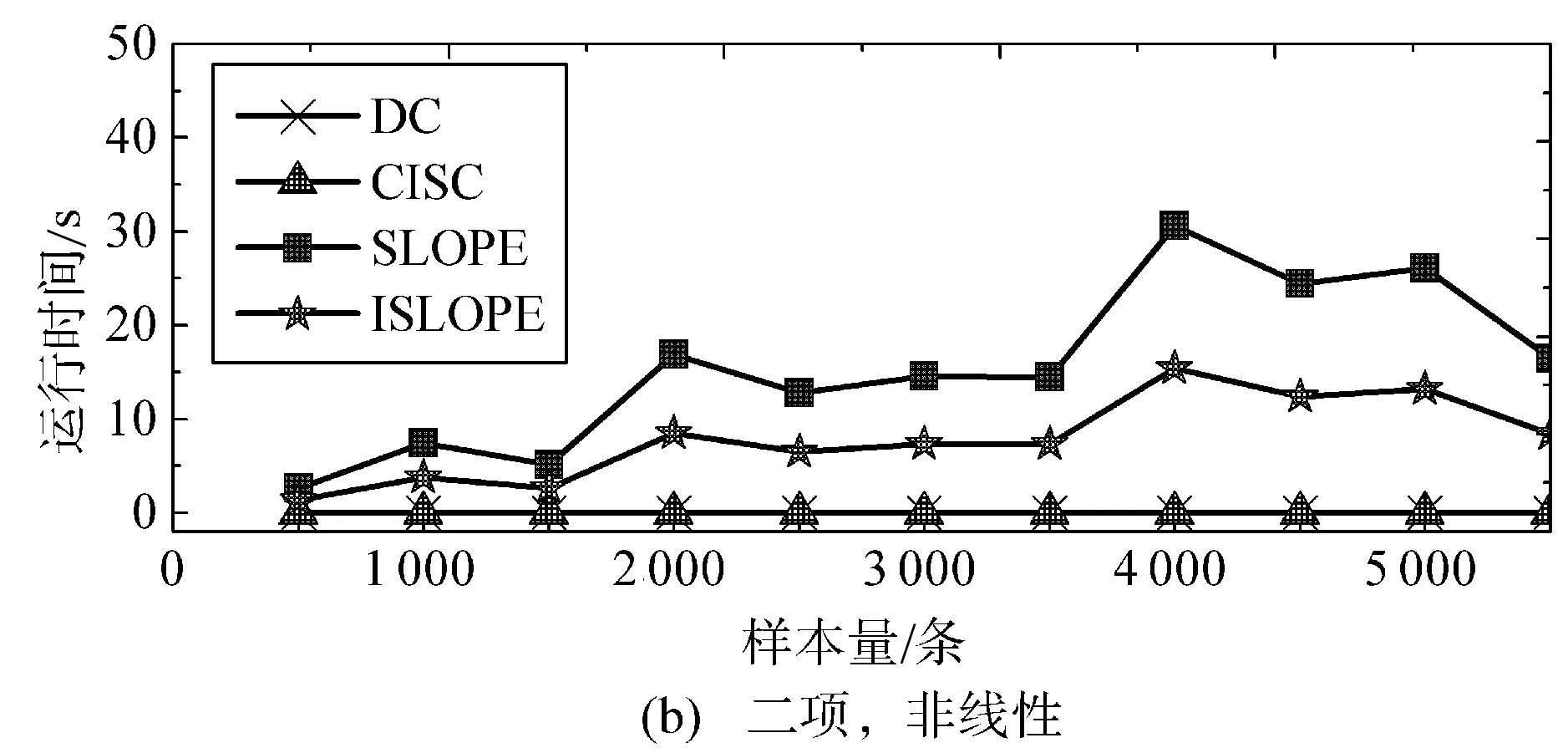
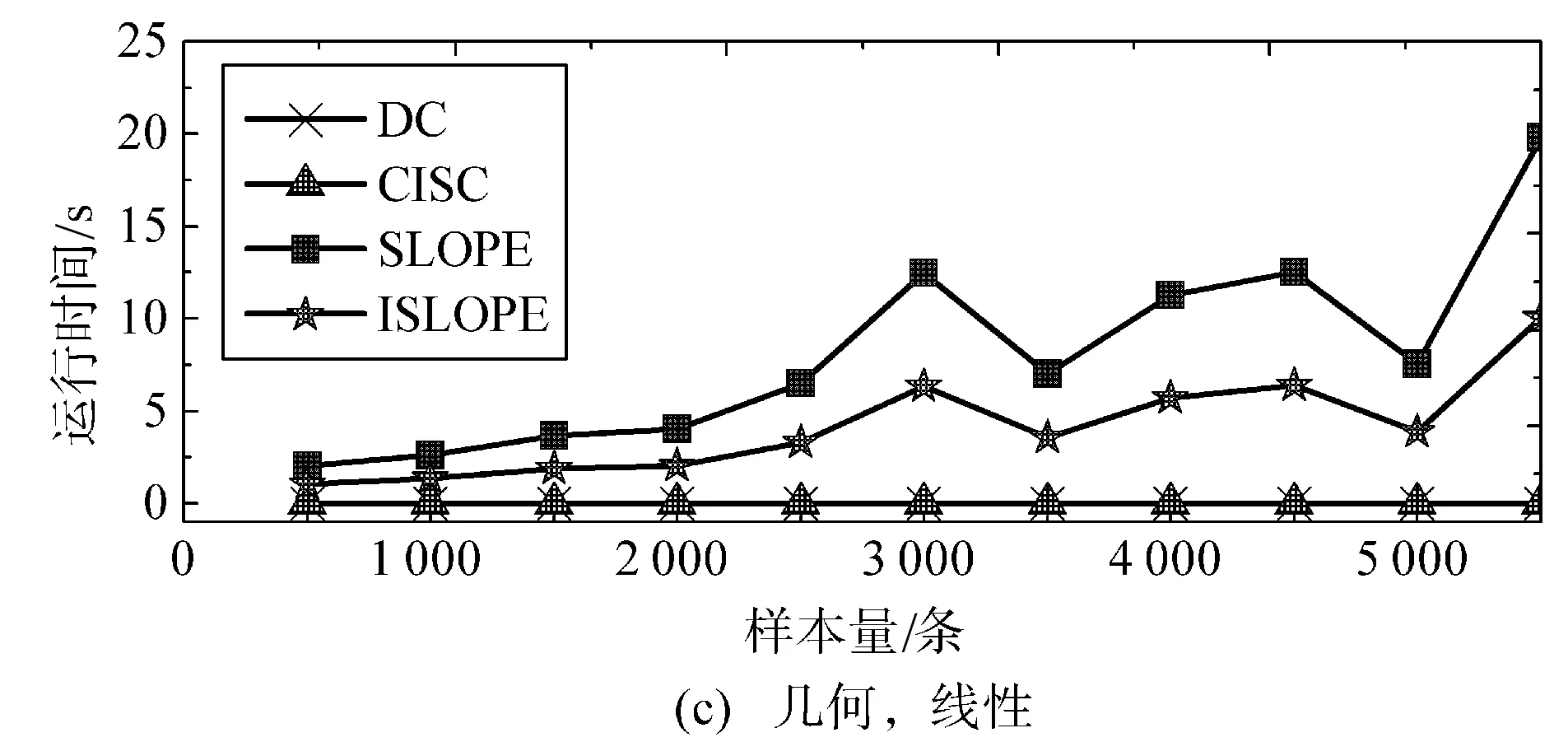
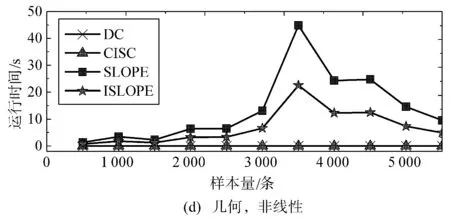
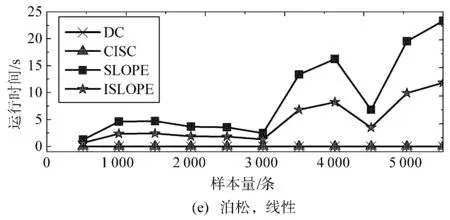

3.4 稳定性
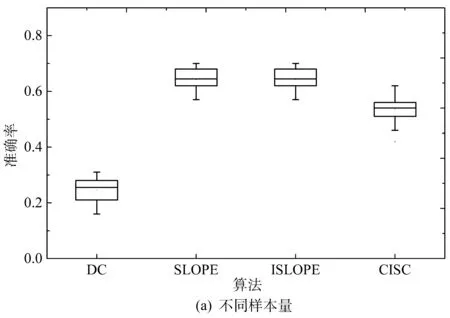
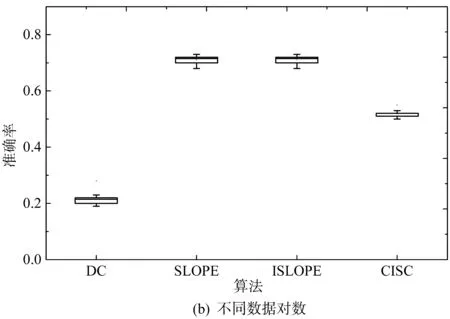
3.5 真实数据


4 结 语

