基于实测交通拥堵数据的城市桥梁多车道横向折减系数研究

李天华，田震欧，张可佳，赵信，白文英

（1新疆城建试验检测有限公司，新疆乌鲁木齐 830000；2重庆交通大学土木工程学院，重庆 400074）

0 引言

桥梁在设计时通常按最不利位置布置其各车道上的车辆荷载。计算城市桥梁荷载效应时，以各加载车道内同时出现最不利荷载为原则，把构件某截面的荷载效应影响线进行加载，再以内力计算结果乘以多车道横向折减系数来计算桥梁整体荷载效应。多车道横向折减反映了桥梁上行驶的车辆荷载使桥梁构件的某个截面产生最大效应时，其同时处于最不利位置的可能性大小[1]。因此，车道数愈多，折减系数愈小，反之，车道数愈少，折减系数就愈大。

多车道横向折减系数的取值大小直接影响到桥梁的承载能力设计与结构安全度。鲍卫刚等[2]以可靠性理论和实测的车辆荷载数据为基础，推导了公路桥梁车辆荷载多车道横向折减系数的理论计算公式。杜柏松等[3]根据实测交通量采用回归分析拟合最大荷载与均值及标准差之间的关系式并获取车重样本的变异系数变化情况，进一步采用概率算法得出了多车道荷载横向折减系数。但基于可靠性理论计算所得到的横向折减系数仍缺少实际工程案例给予充分证明。为此，笔者基于三个月的城市桥梁实测拥堵车辆荷载数据，建立不同车道的拥堵荷载模型，分析各车道荷载效应并统计其并行概率，基于横向折减为其他车道最不利荷载效应依次向主车道折减这一原则，定义城市桥梁拥堵车辆横向折减系数为：当拥堵车辆荷载布满桥上所有车道时，根据各个车道的真实车辆拥堵模型对桥梁产生的荷载效应与最不利情况下多车道荷载模型对桥梁产生的荷载效应之比，计算出城市桥梁多车道横向折减系数，为现行规范修订提供参考。

1 特征值分析与模型建立

本文通过人工现场采集交通拥堵车列，经图像处理分别提取出第一车道（L1）、第二车道（L2）、第三车道（L3）、第四车道（L4）及多车道（L1-4）拥堵车辆的车-桥距、轴距、车间轴距、轴重信息。

1.1 车-桥距

车-桥距是指车辆的前轴或者后轴至桥头或者桥尾的距离，如图1所示可以分为a、b、c、d四种情况。

图1 车-桥距示意图

车桥距一定程度上真实地反映出城市桥梁观测区间中拥堵车列的纵桥向分布情况。在进行车-桥距的统计分析前，剔除车头尾距大于5m及以上的无效数据，对经过整理的车头尾距数据采用K-S检验法分别按正态、对数正态、伽马、威布尔和极值I型5种分布类型进行分布拟合检验。采用极大似然估计得出具有95%保证率的分布参数，分布参数的取值及其置信区间，见表1。将分布参数代入各分布的概率密度函数，得出车-桥距参数分布概率密度函数的具体表达式，根据最不利原则即纵桥向尽可能多的布载，通过MATLAB软件求各分布函数的0.05分位值即为车桥距代表值。

表1 车-桥距概率分布类型及分布参数

1.2 轴距

轴距决定了拥堵车辆荷载在桥跨上排列的间距。由于本文选用车辆类型相对常见，在不具备逐个称重的条件下，亦可根据查询出厂参数来确定。小汽车的轴距和中、大型客车的轴距相差甚大，因此分开进行分析。

（1）小汽车轴距

对经过整理的轴距数据采用K-S检验法分别按正态、对数正态、伽马、威布尔和极值I型5种分布类型进行分布拟合检验，结果十分不匹配，故在确定轴距参数的代表值时，考虑到采用样本总量的均值并不能反映轴距参数样本内某些数值的显著性，因而本文采用求样本的加权平均值，得到的轴距参数加权平均值即作为各自轴距的代表值，见表2。

图2 车间轴距示意图

表2 小汽车轴距频数分布区间的权重系数及代表值

（2）中、大型客车轴距

由于观测的中型客车和大型客车车型比较单一且样本总量很少，无法对其进行统计分析。因此本文以三个月所观测到的具体车型的出场参数为依据，对于轴距直接取平均值并经适当取整作为中、大型客车的轴距代表值，见表3、表4。

1.3 车间轴距

车间轴距代表相邻两辆车间前车后轴至后车前轴的距离，即等于相邻两车辆的车距与车辆前悬值和后悬值三者之和，如图2所示。

在进行车间轴距的统计分析前，剔除车间轴距大于6m及以上的无效数据，因为其不利于反映出城市桥梁车辆拥堵的状态。由于不同车型的悬值差异较大，因此不能只采用单一车间轴距代表值而是要针对同一车型间和不同车型间分别采用不同的车间轴距代表值。本文共划分了三种车型，以[1m，4m]、[4m，5m]和[5m，6m]来作为小汽车间，中型客车间和大型客车间的车间轴距样本数据。通过各区间统计数据的加权平均值得到三个同一车型间的车间轴距代表值，再由已知两车型间的车间轴距代表值的均值来确定不同车型间的车间轴距代表值，见表5。

表3 中型客车轴距代表值

表4 大型客车轴距代表值

表5 不同车型间的车间轴距代表值

1.4 轴重

轴重直接影响桥梁的受力状态。由于观测区间车辆类型相对常见且小汽车与中、大型客车轴重相差较大，在不具备逐个称重的条件下，根据出厂参数获取到的车辆整备质量样本库为数据基础来分别确定小汽车和中、大型客车的轴重代表值。

（1）小汽车轴重

查阅车辆出厂参数获取车辆的整备质量（自重），采用常见的前置发动机前轮驱动型式的轴荷分配值（49%和51%），即假定为前后轴载荷分配相等，对空载轴重参数的样本库进行统计分析得到其代表值。根据《汽车道路道路试验方法通则》中规定乘客质量取60kg/人，由空载轴重的代表值加上车辆满载5人时的质量得到满载轴重代表值。

车辆空载轴重采用非参数的核密度估计法来对空载轴重参数进行统计分析[4]，空载轴重参数核密度估计的核函数K（.）均采用高斯核函数（Gaussian），并调整空载轴重参数带宽，使之拟合曲线较为光滑且能反映出大部分数据所包含的信息，通过编制MATLAB计算程序得出空载轴重参数的期望值见表6，并适当取整作为各自的代表值。

表6 小汽车空载轴重参数期望值及代表值

（2）中、大型客车轴重

中、大型客车的样本总量很少，故以三个月观测采集数据直接取平均值的方式来确定其轴重代表值。本文是采用根据出厂参数获取客车满载轴重来确定其代表值，因此需对中、大型客车的满载轴重进行系数为0.8的折减。按分配系数50%（即前后轴平均受力）来计算轴重，并经适当取整来作为中、大型客车的轴重代表值，见表7、表8。

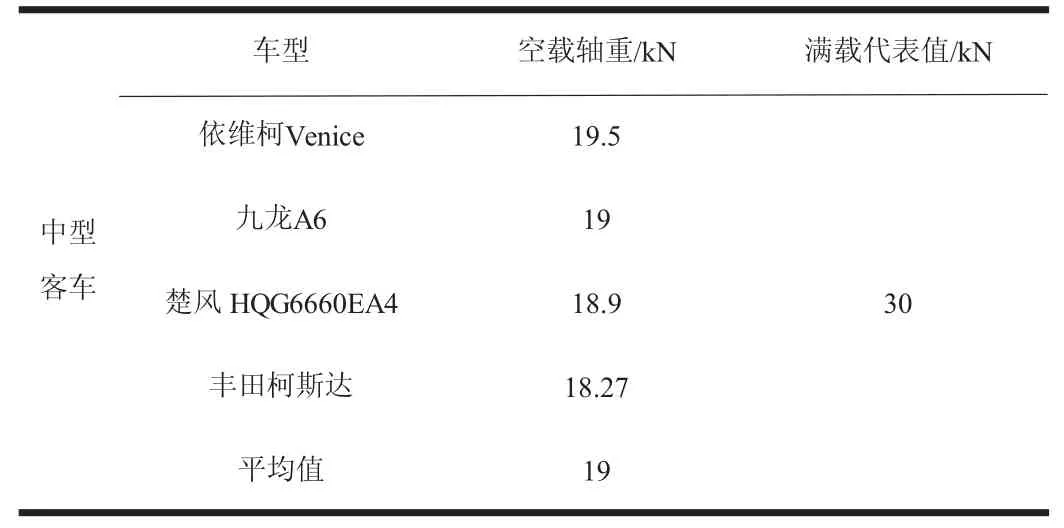
表7 中型客车轴重代表值

表8 大型客车轴重代表值

1.5 拥堵荷载模型

交通流是由各种型号的车辆混合而成，是一随机现象。《公路桥涵设计通用规范》[5]（JTGD60-2004）中把大量、经常出现的汽车荷载排列成车队形式，作为设计荷载。本文根据已有的数据和城市桥梁的特点，结合已知车型间的各类参数代表值，拟定如下几种常见的对城市桥梁会产生一定损害且出现频率较高的拥堵车辆模型[6]，见表9。

表9 城市桥梁车辆拥堵模型

2 荷载效应计算

本文数据收集和荷载效应计算分析所使用的桥梁计算模型是位于乌鲁木齐市中心城区的西大桥，原形跨径组合：10m+30m+10m，三跨等截面钢筋混凝土连续梁桥，桥面有效宽度12.5m，T形主梁高1.98m，C50混凝土，柱状桥墩。通过有限元软件MIDAS建模时采用2.5m梁单元，支座负筋节点处进行加密处理，中跨有横隔梁4道，如图3所示。

图3 西大桥MIADAS模型整体图

对桥梁模型上的四个单车道和多车道分别进行M1（全部由小汽车排列形成的拥堵荷载）、M2（由小汽车和一辆大型客车为中心排列形成的拥堵荷载）、M3（由小汽车和大型客车依次混合排列形成的拥堵荷载）、M4（由小汽车和一辆中心客车、一辆大型客车为中心排列形成的拥堵荷载）、M5（由小汽车、中型客车、大型客车依次混合排列形成的拥堵荷载）、M6（全部由大型客车排列形成的拥堵荷载）6种拥堵荷载模型下的荷载效应分析，见表10—表14。

表10 第一车道在六种拥堵荷载模型下的荷载效应

表11 第二车道在六种拥堵荷载模型下的荷载效应

表12 第三车道在六种拥堵荷载模型下的荷载效应

表13 第四车道在六种拥堵荷载模型下的荷载效应

表14 多车道在六种拥堵荷载模型下的荷载效应

把四个单车道同时作用相同拥堵类型的荷载模型，计算其各个车道的跨中正弯矩叠加组合，见表15。在相同拥堵类型的前提下，车道荷载效应叠加组合成的各车道跨中正弯矩值与多车道荷载效应中各车道的跨中正弯矩值十分相近，其微小的差距是由于每个车道上的拥堵荷载模型的不同而造成的，属于合理范畴，因此可认为各个车道上的拥堵车辆荷载加载是互不相关的，属于独立重复事件。

表15 荷载效应组合与多车道荷载效应跨中弯矩对比

3 横向折减系数

拟定第一车道为主要车道，第二、三、四车道分别向第一车道折减。分别统计出当主车道在M1、M2、M3、M4、M5、M6拥堵模型时，其余三条单车道出现各个不同单车道拥堵模型的概率，每条车道分别选取其单车道拥堵荷载模型中出现概率最高的拥堵模型，由此布满所有车道，组成的各车道荷载效应与多车道不同拥堵模型下的荷载效应作比较，得出6种不同拥堵情况下的横向折减系数取其平均值，为最终的城市桥梁车辆拥堵横向折减系数，见表16—表22。

表16 主车道为M1拥堵模型时的折减系数

表17 主车道为M2拥堵模型时的折减系数

表18 主车道为M3拥堵模型时的折减系数

表19 主车道为M4拥堵模型时的折减系数

表20 主车道为M5拥堵模型时的折减系数

表21 主车道为M6拥堵模型时的折减系数

表22 城市桥梁多车道横向折减系数

表23 我国车道横向折减系数规范值

对比表22和表23，我们发现通过本文计算方法所得到的多车道横向折减系数比我国《公路桥涵设计规范》[8]中的规范值要普遍偏小0.1～0.2，这是由于本文数据采集对象为城市桥梁，其车型相对单一且受交通管制影响不会出现重型或超重车辆，各车道的最不利荷载效应不会出现巨大差幅，因此基于概率统计的横向折减效果更为显著。

4 结论

1）以一种较为可靠的城市桥梁拥堵车辆交通荷载数据的人工采集方法，结合概率统计法可准确快速地提取车辆拥堵交通荷载中车型、车-桥距、轴距、车间轴距、轴重等参数信息。

2）通过分析拥堵车辆荷载参数，考虑拥堵对桥梁的影响以及现场实际情况，模拟出了6种常见的城市桥梁车辆拥堵模型。

3）通过荷载效应组合对比分析，证明了各个车道上的拥堵车辆荷载加载是互不相关的，属于独立重复事件，因此可根据实际工况下桥梁各车道不同拥堵模型并行的概率，计算出城市桥梁多车道横向折减系数为：1.00、0.87、0.68、0.47。对比发现城市桥梁受车型影响横向折减值比现行设计通用规范值小，折减效果更为显著。