底水油藏油井见水时间预测
袁清芸
(中国石化西北油田分公司勘探开发研究院,新疆乌鲁木齐 830011)
在底水油藏开发中,油井见水时间预测对油藏管理具有十分重要的指导意义。不少学者给出了底水油藏见水时间预测公式[1-7],本文认为李传亮推导的计算公式机理明确,可操作性强,更适合油田开发实际管理工作,因此本文以李传亮的公式为基础,根据渗流学及流体力学原理,建立了底水油藏见水模型(图1)并推导出了见水时间公式。

图1 油藏底水锥进模型示意图
1 见水时间预测模型
1.1 无夹层见水时间计算模型
对于无夹层油藏,底水锥进的速度为:
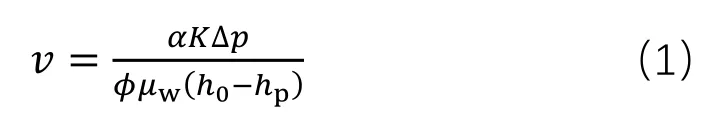
根据油井稳定生产时的产量公式可得到生产压差∆-:
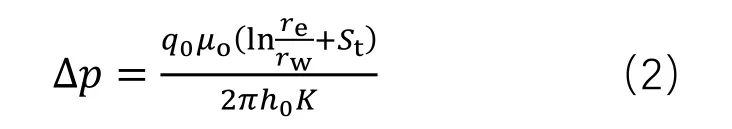
底水9点锥进至井底:点(图1中垂直距离)所需时间[8-9]即为见水时间;<=:
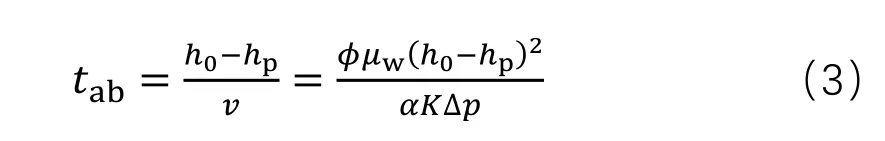
将公式(2)代入(3)整理得到:
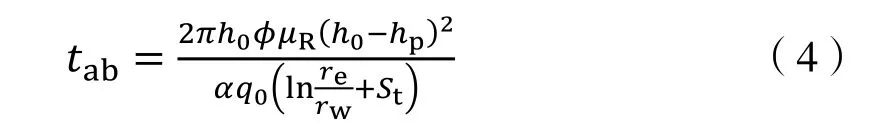
如果考虑底水上升过程中存在油水两相流,则:

1.2 有夹层见水时间计算模型
底水油藏中存在夹层时,底水锥进至井底需要两个过程:先是底水锥进过程(由9点到:点),然后是平面推进过程(由:点推进至F点),见水时间包括底水锥进时间;<=和平面推进时间;=G。因此夹层展布范围及位置对油井见水时间具有较大影响[8-10]。其中公式(7)中忽略井筒半径HI。
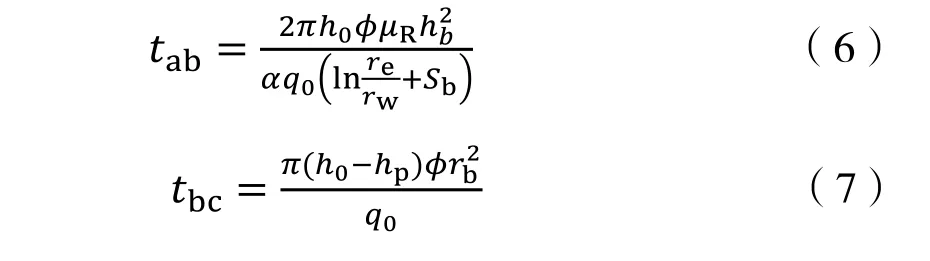
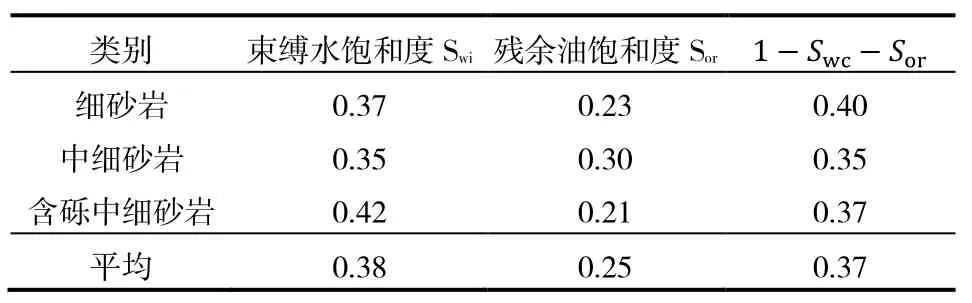
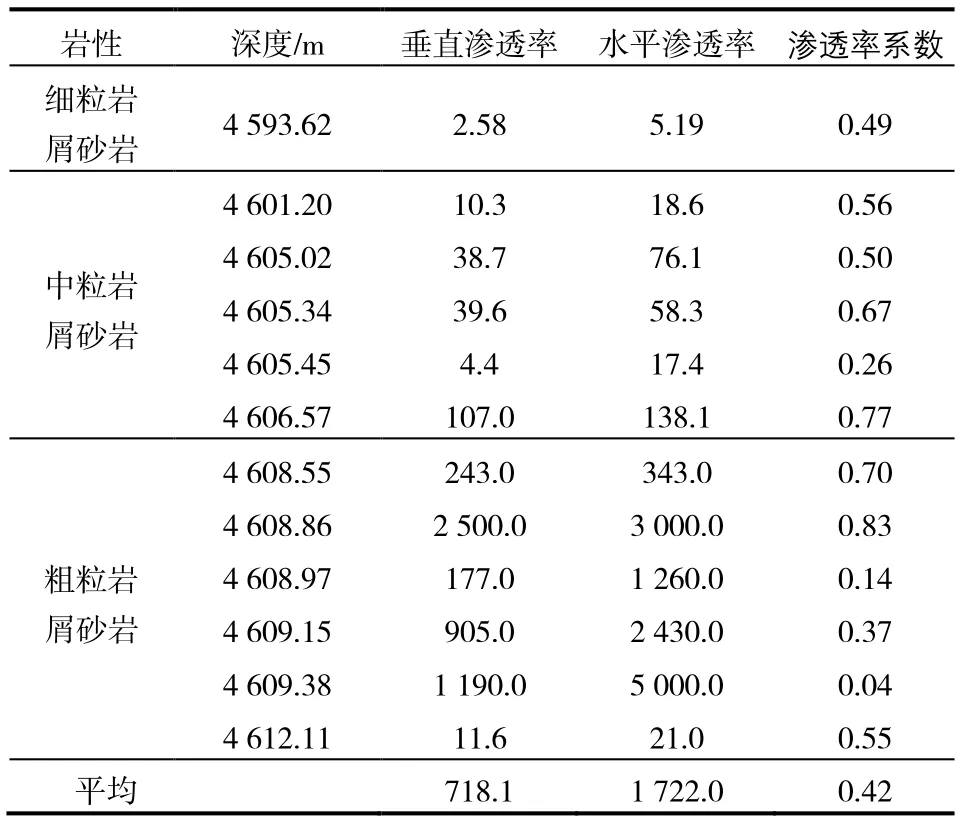
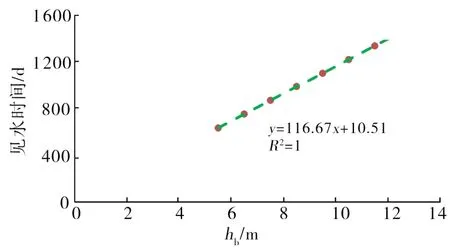
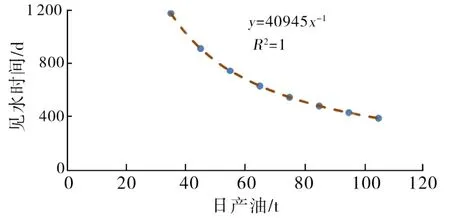
将两个公式相加,得到见水时间; 如果考虑底水上升过程中存在油水两相流,则:得到 设置油层打开程度:=ℎR/ℎS,那么上式中的(ℎS−ℎR)/ℎS=1−:,上式变为: 上述式中:!为水锥速度,m/ks;WI、WZ分别为地层水、地层原油黏度,mPa·s;WX为水油黏度比;∆-为油井生产压差,MPa;]Z为油井产量,m3/ks;_为地层(水平)渗透率,μm2;V为孔隙度;为油层渗透率系数;Y`、Y=分别为油井的总表皮因子、夹层的表皮因子;YIG为束缚水饱和度;YZ[为残余油饱和度;ℎZ为油水界面到射孔井段顶的距离,m;ℎR为射孔井段到井底的距离,m;ℎ=为夹层到油水界面的距离,m;Ha为油井泄油半径,m;H=为夹层边缘到油井距离,m;:为油层的打开程度。 以X研究区为例,确定模型主要参数。X研究区为三叠系强底水砂岩油藏,油藏厚度10~20 m,夹层发育。根据见水时间公式(10),需要确定水油黏度比WX、孔隙度V、(1−YIG−YZ[) 、油层渗透率系数 4个主要参数。其中,前期实验证实WX在地下条件基本稳定,因此重点对V、(1−YIG−YZ[) 、油层渗透率系数的取值开展研究。 根据实验资料,研究区孔隙度主要集中在0.22~0.23,但孔隙度在地层覆压下存在一定损失,故实际应用中需要对孔隙度参数进行适当的修正。研究区三叠系下油组储层覆压下孔隙度损失率与地面气测渗透率相关性好,50 MPa下孔隙度损失率平均8%左右,因此实际计算中需对测井孔隙度进行修正,孔隙度修正值为气测孔隙度的92%。 根据对研究区不同粒径相渗束缚水、残余油饱和度的统计(表1),不同粒径两相流区间的渗束缚水、残余油饱数值差异较大。研究区储层主要以中、细粒砂岩为主,粗砂岩油层较薄,根据表1认为,两相流区间以中、细砂岩为准,(1−YIG−YZ[)应在0.35~0.40之间,最后取平均值0.37。 表1 研究区不同粒径相渗束缚水、残余油饱和度 根据不同粒径下实验测试渗透率值(表2),得到平均渗透率系数为0.42。 表2 研究区不同粒径相渗透率对比 10-3μm2 选取研究区内3口井验算核实,分别是2口直井A井、C井和1口水平井BH井。这3口井测井解释均钻遇夹层,并且根据邻井钻遇夹层情况和数值模拟及历史拟合情况,能够确定钻遇夹层半径,最后可根据前面推导出的具有夹层的油井见水时间公式和表3中各井参数,预测3口井的见水时间。对比表明,计算见水时间和实际见水时间的最大相对误差为8.4%,最大绝对误差21.1 d,因此认为计算公式基本满足实际要求,具有较强应用性。 对于底水油藏,油井见水时间受到多因素的影响。根据公式(10),夹层半径H^、夹层距油水界面距离ℎ=、油井日产量]Z对见水时间; 表3 3口井见水时间对比 图2 见水时间随ℎ=变化趋势 图3 见水时间随]Z变化趋势 图4 见水时间随H=变化趋势 (1)以李传亮推导的见水公式为基础,推导出了底水油藏见水时间预测公式;结合研究区地质情况,对 φ,(1−YIG−YZ[),α三个参数进行修正,使公式更符合实际油藏情况。 (2)实例计算表明,利用本文的公式计算见水时间与实际见水时间相对误差不大于9.0%,能够满足实际工作要求。 (3)对于发育夹层的油井,夹层半径对见水时间影响特别敏感,本文公式在预测油井见水时间的同时,也可用于验证夹层实际展布范围。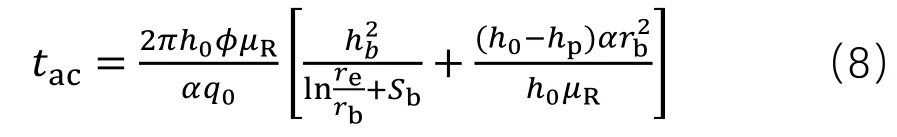
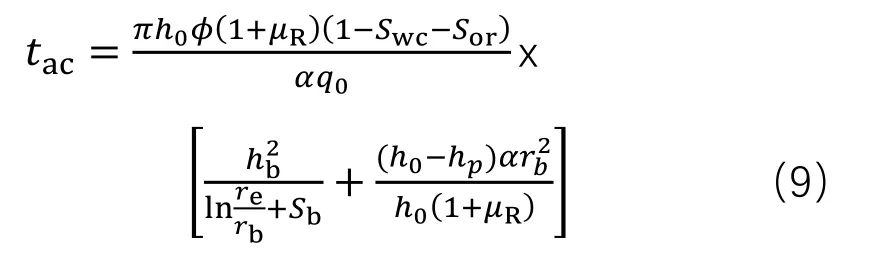
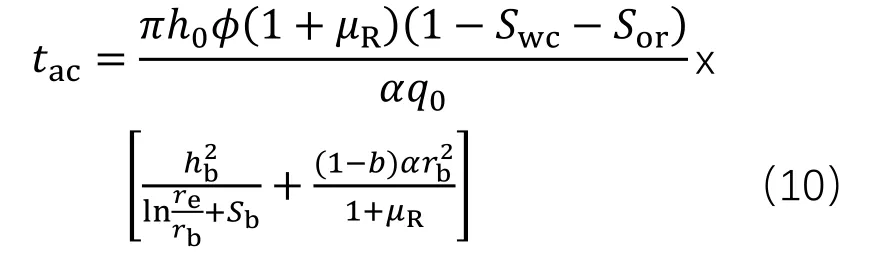
2 模型参数的确定
2.1 孔隙度的确定
2.2 (1−YIG−YZ[)的确定
2.3 渗透率系数(垂向渗透率与水平渗透率比值)
3 应用实例

4 结论

