基于扩展双谱的齿轮压缩采样信号特征提取方法

李 飞，秦国军，庄圣贤

（1.西南交通大学 电气工程学院，成都 610031； 2.湖南纬拓信息科技有限公司，长沙 423038）

压缩感知(Compressed Sensing)是D Donoho、E Candés及华裔科学家T Tao等人在2006年提出的一种突破了传统香农－奈奎斯特信号采样定理的信息获取与数据采集理论，其核心思想是将压缩过程和采样过程合并，直接针对信号所蕴含信息进行采样，然后根据相应的重构算法恢复出原始信号[1–3]。但目前压缩感知重构算法都存在一些无法改善的缺点，如算法复杂、重构误差、含噪信号重构效果差等[4]。

双谱是高阶谱中应用最广泛的一种分析方法，在理论上可完全抑制高斯噪声，且保留了相位信息，可定量描述信号中的二次相位耦合，是分析非线性、非平稳信号的有力工具，在故障诊断及特征提取领域的应用研究不断发展[5–6]，取得了较理想的应用效果。

本文提出一种基于扩展双谱的压缩信号特征提取方法，避免了尚存问题的信号重构过程，直接对压缩信号进行分析。仿真及工程应用均表明了该方法可以有效地提取压缩信号故障特征，为机械故障诊断提供有力的依据。

1 扩展双谱的基本原理

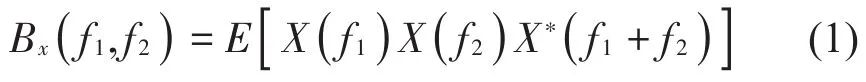
式中：E[]表示数学期望，f1和f2为频率变量，表示频谱，的复共轭。

为了实现压缩信号的特征提取，需对双谱的定义进行推广。如果权重因子{w1,w2,w3}满足，则基于权值的扩展双谱可以定义为

很明显，双谱是权重因子均取1时的扩展双谱特例。当w1=w2=1，w3=2时，另一种双谱，中频双谱(Middle frequency bispectra，MFB)可以定义为

1.1 压缩采样

与传统模数转换过程不同，压缩感知理论采用模拟信息转换器实现由模拟信号到信息的转换(Analog to Information Conversion，AIC)。调制宽带转换器模型(Modulated Wideband Converter，MWC)是一种较成熟的模拟信息转换模型，硬件实现较简单，特别适合信号频域信息的采样及重构，本文采用MWC模型实现压缩采样。

图1 调制宽带转换器系统框图

在调制宽带转换器采样系统中，信号x(t)同时由m路采样通道采集。各支路中的信号x(t)首先与伪随机序列pi(t)混频实现频谱搬移，使低频段包含整个频谱范围的信息。

M序列是一个常用的伪随机序列，具有结构简单，易于硬件实现等优点，因此采用M序列作为混频函数，其周期为Tp，幅值随机取±1，每个周期分为W个等间隔区间，可将其表示为

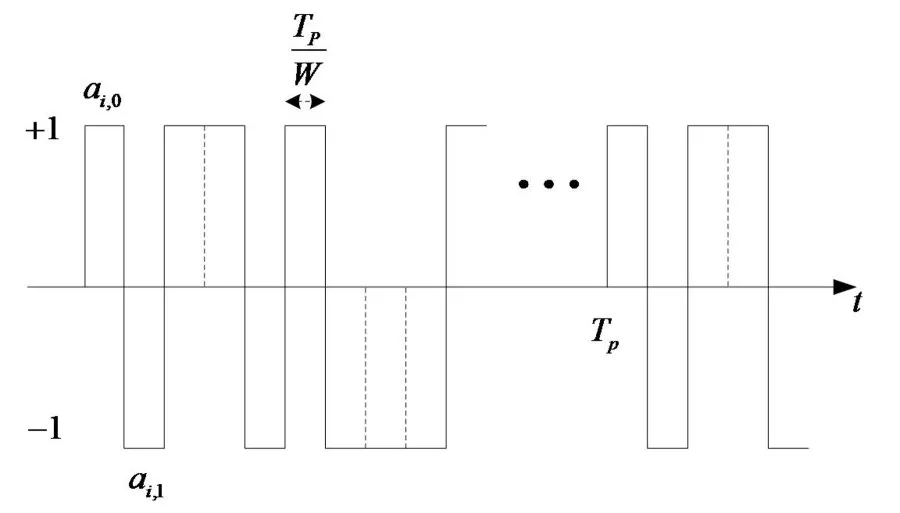
图2 混频函数pi(t)

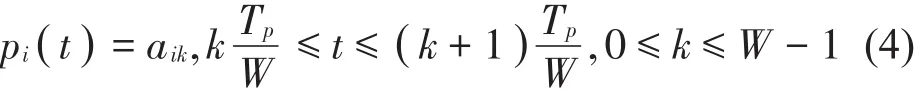
pi(t)频谱由一系列间距为fp的谱线组成，其傅立叶级数为

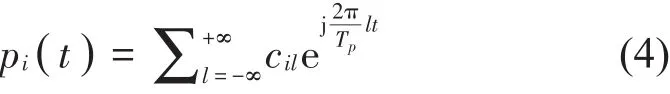
式中傅立叶系数cil随频率而变化，可表示为

以fp=3 kHz的M序列为例，其频谱由一系列间距为fp的谱线组成，如图3所示。

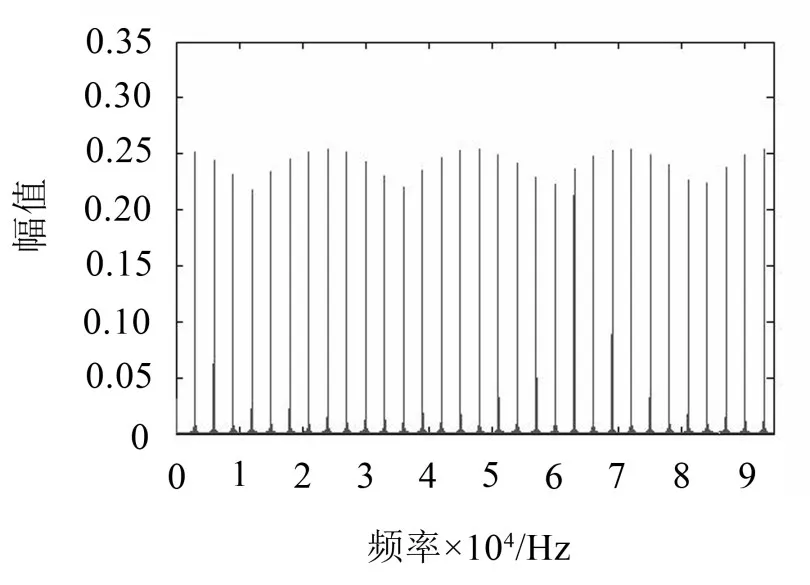
图3 fp=3 kHz的混频函数频谱图

混频后信号经过一个低通滤波器滤掉高频部分，再通过采样率为fs的低速ADC进行采样，获得m组不同的低频采样序列yi[n]，至此完成了原始模拟信号到压缩感知信息的转化过程，即压缩采样过程。

1.2 压缩信号的扩展双谱分析

令原始齿轮振动信号为x(t)，齿轮转频为fr，齿数为Z，混频M序列为m(t)，周期fp=Zfr。

忽略测量噪声，x(t)的频谱可以表示为

混频时原始信号与混频函数在时域上相乘，即在频域上作卷积。由于混频函数频谱为一系列间距为fp的谱线，因此频域卷积相当于将原始信号频谱进行多次搬移并叠加，搬移量为kfp，k=±1，±2，±3，…。混频后信号的离散傅立叶变换为

通过低通滤波器后，采样序列yi[n]的离散傅立叶变换为

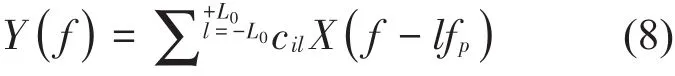
根据式(5)，式(6)及傅立叶变换性质，可将式(8)表示为

当频率为mfr时可表示为

在频率对(m1fr,m2fr)处的双谱为

齿轮振动信号这样的相位耦合信号，其相位满足

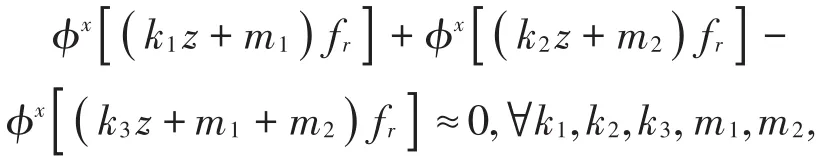
故

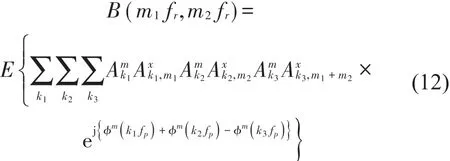
当M序列一个周期中脉冲数足够多时，其在kfp处的相位谱总是均匀分布在( ]-π,π ，故

由上式可知，传统双谱无法表现相位耦合现象，因此需要另一种类型的双谱—中频双谱。

2 实验分析

2.1 仿真分析

下面对齿轮振动仿真信号x(t)进行分析，其表达式如下

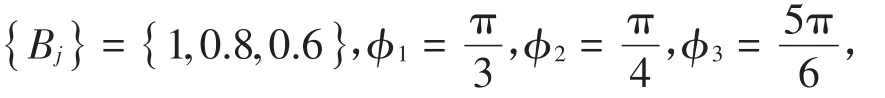
Z=23，n(t)是高斯分布噪声。

仿真信号及其频谱如图4所示，图中可以看到与115 Hz，230 Hz，345 Hz相对应的三个谱峰及边频带分量。

令M序列一周期脉冲数W=63，则其时钟频率应为5 Hz×23×63=7.245 kHz。M序列及其频谱如图5所示，其频谱间隔为115 Hz。63个正交M序列的相位谱如图6所示，其相位谱均匀分布在(0，2π]。混频信号及其频谱，滤波后频谱如图7所示：

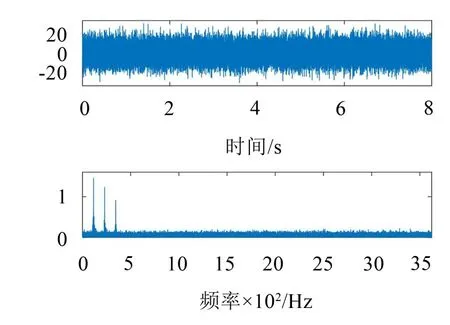
图4 x(t)及其频谱图

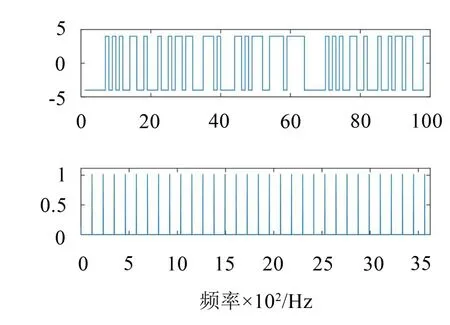
图5 m(t)及其频谱图

图6 M序列前5个谱线相位谱分布

图7 混频信号及其频谱，滤波后频谱

对混频信号进行中频双谱分析，结果如图8所示。

图8 混频信号中频双谱

上图可明显看到在(5 Hz，15 Hz)，(5 Hz，25 Hz)，(10 Hz，20 Hz)处存在3个与(fr，3fr)，(fr，5fr)及(2fr，4fr)对应的谱峰。因此，中频双谱可以用于识别相位耦合，即齿轮故障识别。

2.2 实验数据分析

实验数据来自英国哈德斯菲尔德大学，包括齿轮磨损整个生命周期的数据，试验台系统由两个串联安装的工业齿轮箱组成，如图9所示，主要参数如表1所示。

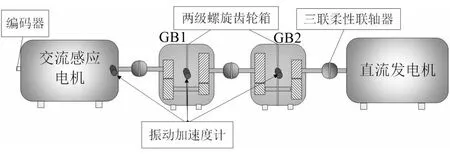
图9 试验台系统示意图

表1 试验台主要参数

利用GB2齿轮自然磨损的振动信号进行分析，图10为其时域及频谱图。原始信号有两级啮合频率，这里只需要分析与故障更相关的一级啮合频率及其谐波，不相关部分通过低通滤波滤掉。

为了保留相位耦合信息，混频M序列时钟频率应为63×fm1，频谱间隔fm1=200.36 Hz。对混频信号进行中频双谱分析，其结果如图11。

由于转速波动及异常频率影响，中频双谱图中无法看到明显的故障特征，需对方法进行改进。

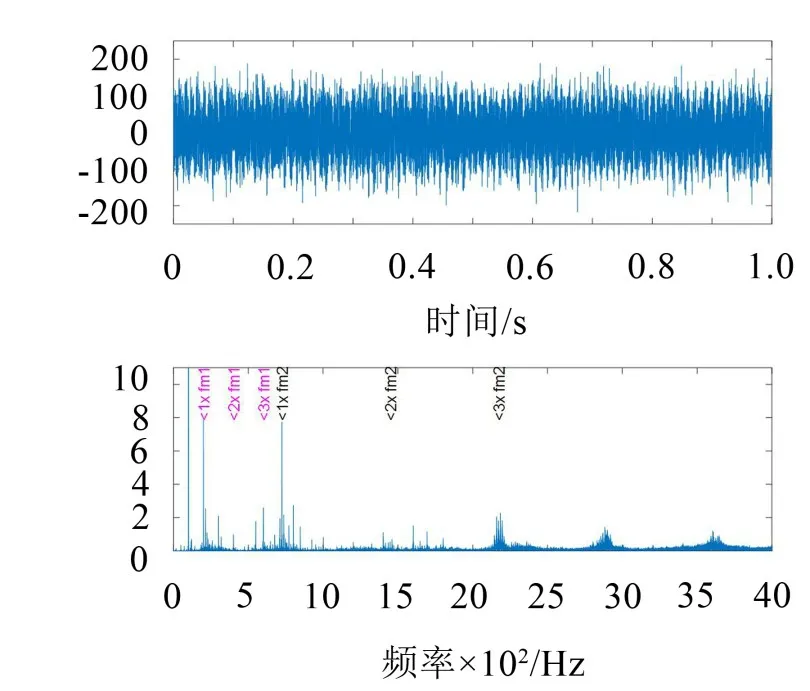
图10 振动信号及其频谱

图11 混频信号中频双谱

2.3 方法改进及验证

为了消除转速影响，引入阶次分析，将信号从时域转化为角度域，从频域分析转化为阶次域分析。同时采用角域同步平均，以加强与转速相关的同步振动分量，减小非同步分量及噪声。其原理框图如图12所示。

图12 改进方法原理框图

振动信号阶次谱及滤波后阶次谱如图13所示

图13 振动信号阶次谱及滤波后阶次谱

混频M序列时钟频率应为63×fm，频谱间隔fm=13。M序列及混频信号阶次谱如图14所示

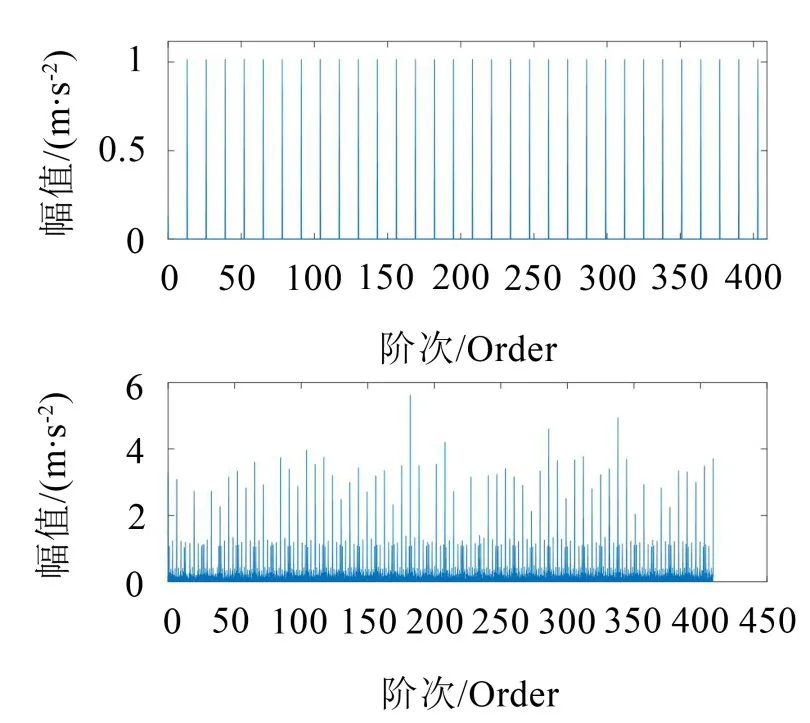
图14 M序列阶次谱及混频信号阶次谱

混频信号通过截止频率为5的低通滤波器后进行低频采样，再通过角域平均消除非同步分量，得到角域压缩信号，结果如图15所示

图15 滤波及平均后混频信号阶次谱

对角域压缩信号进行中频双谱分析，不同故障阶段的结果如图16所示。

图16 滤波及平均后混频信号阶次谱

可以看到在(3，1)，(2，4)和(5，3)处存在3个与(3fr，fr)，(2fr，4fr)及(5fr，3fr)对应的谱峰，其幅值随故障程度而明显增加，可用于识别齿轮故障。

3 结语

本文对齿轮压缩信号频域特性进行了研究，对压缩信号特征提取方法——中频双谱进行了理论推导，通过仿真及实验验证了方法的有效性。

（1）满足一定条件的混频M序列能将高频信息搬移到低频并保留相位耦合特征，中频双谱能够提取压缩信号中的相位耦合特征，识别齿轮故障。

（2）虽然实际应用中存在转速波动，非相关分量的影响，但这些问题可以通过引入阶次分析，角域同步平均等技术消除，得到很好的结果。