基于Sobel算子的Criminisi改进算法

崔天卿 许 凯 阎 石

（兰州大学信息科学与工程学院 兰州 730000）

1 引言

随着计算机技术的发展，数字图像修补技术相较传统的手工修补图像，在修补时间与修补结果上都有着明显的优势，这使得该技术得到迅速发展并且成为了数字图像技术中的一大研究热点。图像修补技术的应用很广泛，可用于处理图像中的划痕、破损、遮挡物等，在文物保护、影视作品制作、文本去除、图像传输等领域中都有着很好的应用［1］。

图像修补技术的基本思想是利用图像中的已知区域来修补缺失的待修补区域［1］，根据所需处理的待修补区域的尺寸不同分为两类：

第一类是用于修补小尺寸破损区域的修补算法，此类算法主要是基于扩散的思想，将已知区域的像素值以一定的传播条件扩散到待修补区域中以达到修补目的。Bertalmio等引入等照度线作为像素扩散方向来修复图像［2］。Chan等引入整体变分模型（TV）修补破损区域［3］。Zhang等引入调和函数改进TV模型，提高了修补效果［4］。此类方法适用于小尺寸破损图像的修补，如图像中的划痕、文字等。但对于大区域破损图像的修补，该方法的修补结果非常差，往往会产生大片模糊。

为了克服第一类图像修补方法处理大尺寸破损区域时产生模糊的现象，Criminisi等开创性地提出了第二类图像修补方法，即基于样本块的纹理合成的图像修补算法。该思想是将待修补区域分成若干待修补块，选取其中优先权最高的块在图像已知区域中寻找最佳匹配块来填充待修补块中缺失部分的像素［5］。该算法很好地解决了第一类算法在处理大尺寸破损图像时产生的模糊现象，使用恰当的像素值替代了待修补区域中的空白，所得的结果更加符合人眼视觉效果。

然而在Criminisi所提算法中，其优先权模型对于图像边缘部分的辨识能力不足，对于图像的纹理与边缘容易产生错误判断，最终在修补结果中产生纹理延伸现象［6］。Criminisi算法作为当前主流的纹理合成算法，在之后的研究中出现了大量以此为基础的改进算法。其中，Wu等为了更好地保证修补过程中图像的线性结构，引入偏微分方程（PDE）来改进优先权，但是没有提升优先权函数对于图像纹理与边缘的辨识能力［7］。Xu等引入稀疏表示改进优先权，增强了修补过程中对图像结构和纹理的辨识能力，但是缺乏对于图像边缘的识别能力［8］。Meur等引入结构张量改进优先权，使得修补结果在人眼视觉上更加连贯，但是该改进方法对于纹理延伸现象的抑制能力不足［9］。许凯等引入结构相似度改进了传统Criminisi算法中的优先权与匹配块搜索方法，得到的结果满足人眼视觉效果，但算法复杂度较高，计算时间过长［10］。

虽然以上改进算法相较传统的Criminisi算法有更好的修补结果，但对于Criminisi算法优先权定义所存在的对于边缘和纹理的辨识能力不足的问题，以上改进算法没有很好地解决，其仿真结果中出现了一定的纹理延伸现象［6］。所以针对这一问题，本文引入了Sobel边缘检测算子改进优先权模型，增强了其对图像边缘的辨识能力，从而提高了匹配块的选取准确率，有效地改善了图像修补质量。

2 Criminisi算法简介

如图1所示，图像已知区域为Φ，待修补区域为Ω，δΩ是待修补区域的边界，以边界上某点p所确定的图像块Ψp称为待修补块。Ψq是以q点为中心在已知区域Φ中选取的一个匹配块，其大小与Ψp相同用于填充Ψp［6］。

Criminisi算法修补循环如下：

1）确定待修部区域Ω，确定区域Ω与区域Φ的边界δΩ；

2）根据优先权定义计算边界δΩ上所有点确定的待修补块的优先权，将优先权最大的待修补块作为开始修补的块；

3）根据匹配块的搜索方式在已知区域Φ内搜索一个与待修补区域大小相同且最为相似的块，称为匹配块，并将匹配块中的对应像素填充到待修补块的像素缺失位置；

4）重新确定边界δΩ，循环以上步骤直到修补结束。

图1 Criminisi算法修补过程

Criminisi算法中的两个关键步骤：优先权的计算和匹配块的选取。对于边界上的点p∈Ω，定义其所确定的待修补块Ψp的优先权P（p）为

式（1）中C（p）称为置信项，D（p）称为数据项，|Ψp|表示待修补块中像素的总个数，当q∈Ω 时C（p）=0，当 q∈Φ 时C（p）=1，∇Ip⊥是p点的等照度线，np是p点的法向量，α是归一化因子，一般取255［5］。

最佳匹配块需要满足：

其中d(Ψp,Φq)代表两个块的差异，定义为

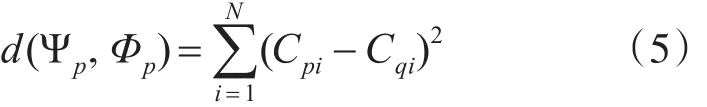
对于彩色图像，分为R、G、B三个通道进行计算：

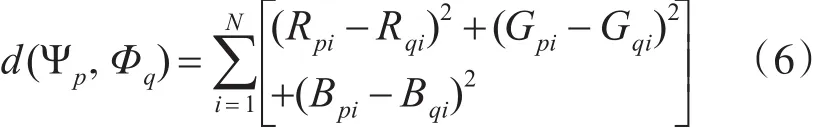
Criminisi算法优先权的定义对图像边缘的识别能力有限，有时会将图像中的纹理部分误认为边缘部分，从而导致在修补结果中产生纹理延伸现象［6］。

如图2圆圈中标示部分所示，由于优先权定义的不足，使得修补结果中出现了明显的纹理延伸现象，破坏了原始图像的结构性。

图2 Criminisi算法修补结果

3 基于sobel算子的改进算法

在传统的边缘检测算子（Roberts算子、Prewitt算子、Sobel算子、Kirsch算子、Canny算子）中，Sobel算子综合各项性能比较下优势明显［11］。因此，本文采用Sobel边缘检测算子进行优先权改进。

3.1 Sobel算子基本原理

首先假设图像是连续函数f（x，y），则连续函数在点（x，y）处的梯度为一个具有大小和方向的矢量，即：

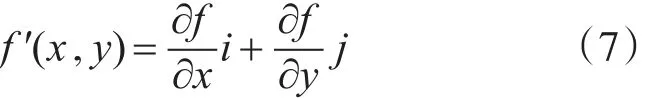
式（7）中i，j分别为x，y方向的单位矢量。点（x，y）处的边缘梯度幅值和方向定义为

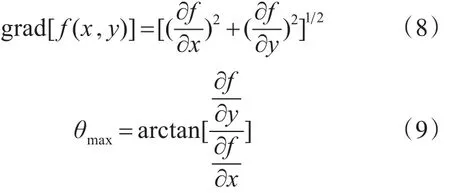
计算出的 grad［f（x，y）］即为图像的边缘数据［11］。

式（8）是假设图像为连续函数，而在实际应用中，采集的图像数据是离散的，因此边缘信息的计算采用相邻或间隔像素的差分值。

以3×3的模板为例，图3中Z5点的Sobel算子边缘信息计算公式如下：

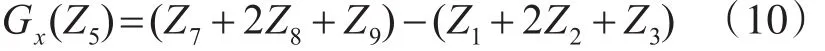
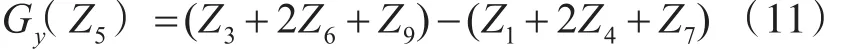
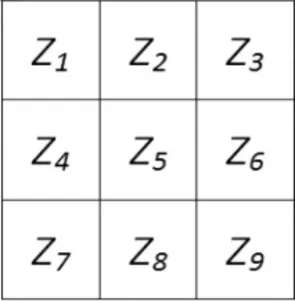
图3 3×3图像模板

Sobel算子是对离散的图像数据进行加权计算，采用如图4所示的模板对待处理图像进行卷积计算，分为水平方向边缘检测和竖直方向边缘检测。

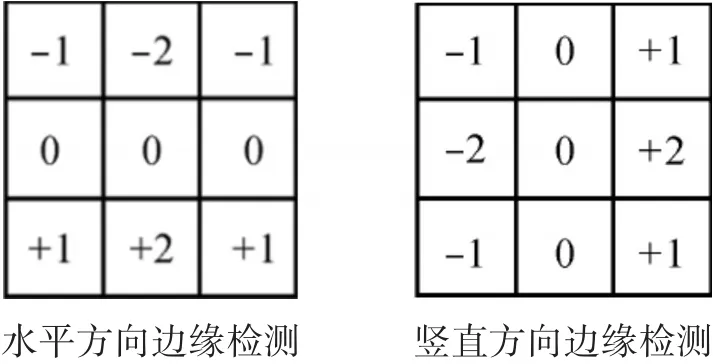
图4 Sobel算子卷积模板

3.2 Criminisi算法优先权改进

定义新的优先权计算公式为

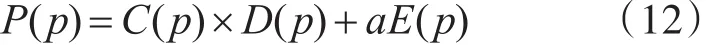
其中E（p）为边缘项，其值为分别用Sobel水平算子和Sobel竖直算子对所选取图像块的卷积之和。

假设选取大小为3×3且以P1、P2点为中心的待修补块如图5所示，其中假设像素值为0的点代表图像的待修补区域，P1、P2点为边界上的点，则根据式（10）、式（11）、式（13）：

图5 分别以P1、P2为中心大小为3×3的待修补块

由式（14）、式（15）计算可得E（p1）=200，E（p2）=600。由于p2点所处位置相较于p1点明显处于图像边缘位置，所以其计算所得的边缘项较大。

式（12）中边缘项E（p）前的乘积项a定义为权重因子，表示边缘项在优先权的计算中所占的比重，权重因子a的引入是因为对于不同的图像，其纹理丰富程度不同，所需的优先权中对边缘的识别能力的大小不同。对同一幅图像，a的取值不同所得的修补结果会产生一定差异。对于不同图像，得到最佳修补结果的a的取值也不相同。

式（12）定义的优先权有以下优先：首先，新的优先权计算方法在引入了边缘项E（p）之后解决了传统Criminisi算法中将图像纹理部分误认为边缘部分从而导致修补结果中出现纹理延伸的问题［6］。

其次，通过对权重因子a的不同赋值，可以对纹理丰富程度不同的图像进行处理。

3.3 改进后的算法流程图

图6 改进的修补算法流程图

4 仿真结果

本文中，通过MatlabR2014b进行算法仿真。仿真过程中选取修补块大小为9×9。

4.1 权重因子a的分析

权重因子a的取值对于修复结果的影响较大，图7是对baboon图像取不同权重值时的修补结果，图（a）中白色部分为待修补区域，图（b）、（c）、（d）、（e）、（f）是权重因子分别取 10-1、10-2、10-3、10-4、10-5时的修补结果，优先权中当C（p）×D（p）项的数量级低于aE（p）的数量级时所得的修补结果更加符合人眼视觉效果。

图7 不同a值下的baboon图像修补结果

实验表明权重因子值的选取是非线性的，根据待修补图像的纹理丰富程度不同，对于同一幅的图像，a值仅在某一特定范围内取值才可以得到较好的修补结果。

图8是对bungee图像取不同权重值时的修补结果，图（a）中白色部分为待修补区域，图（b）、（c）、（d）、（e）、（f）是权重因子分别取10-1、10-2、10-3、10-4、10-5时的修补结果，优先权中C（p）×D（p）项的数量级高于aE（p）的数量级时所得的修补结果更加符合人眼视觉效果。

图8 不同a值下的bungee图像修补结果

根据以上仿真结果，对于不同图像，图像的纹理丰富程度决定了权重因子的选取。当图像纹理丰富程度较强时，a 的取值使得C（p）×D（p）项低于aE（p）项的数量级时所得修补结果最好。当图像纹理丰富程度较弱时，当 a 的取值使得C（p）×D（p）项高于aE（p）项的数量级时所得修补结果最好。

4.2 改进后的算法仿真结果

bungee图中 a 取10-4，baboon图中 a 取10-2。

图9中是对bungee图中进行目标物的移除，（a）为原始图像，（b）中白色的部分为待修补区域，（c）为Criminisi所提算法的仿真［5］，（d）为Wu改进算法的仿真［7］，（e）为许凯改进算法的仿真［10］，（f）为本文改进算法的仿真结果。由图可见，在修补结果中用圆圈圈出的部分即纹理延伸现象在本文中都有很好的改进效果，相较图（e）改进算法［10］，本文算法不仅很好地抑制了纹理延伸现象，在修补时间上也减少到了许凯所提算法［10］的三分之一。

图9 bungee图像修补结果

图10 是对baboon图中的缺失区域进行修补，（a）为原始图像，（b）中白色的部分为图像中缺失的部分，（c）为Criminisi所提算法的仿真［5］，（d）为Wu改进算法的仿真［7］，（e）为许凯改进算法的仿真［10］，（f）是本文改进算法的仿真结果。由图可见，在修补结果中用圆圈圈出的部分即纹理延伸现象在本文中都有很好的修补效果，相较图（e）改进算法［10］，本文算法不仅很好抑制了纹理延伸现象，在修补时间上也减少到了许凯所提算法［10］的三分之一。

图10 baboon图像修补结果

5 结语

本文通过以Sobel算子为基础的边缘项以及权重因子，对优先权函数进行改进，提出了一种新的基于Sobel算子的Criminisi改进算法。通过对权重因子a的不同取值，可以对不同图像进行修复。从仿真结果来看，虽然得到的修补结果符合人眼视觉效果，但权重因子的选择不是自适应的，而是由实验得到的，对于同一幅图像和不同图像，根据图像纹理丰富程度，有不同的权重因子a使得得到的修补结果最好。因此，本文算法的下一步改进工作应该着重于对权重因子a的选取，根据待修补图像的纹理丰富程度与权重因子a的关系做到自适应，从而使改进算法得到更进一步的完善。