基于极线单应性的目标空间定位算法

杨利斌 陈 滨 王 毅

（海军航空工程学院兵器科学与技术系 烟台 264001）

1 引言

立体视觉作为计算机视觉的一种重要形式，在该领域有着广泛的应用前景［1～6］。立体视觉系统中对于图像的获取一般有两种方式：一种是基于单摄像设备［7～10］，随着时间的推移不断变化位置，获取不同时刻同一目标在不同位置的多幅图像，一般适用于目标变化较小的场合；另一种是基于双摄像设备［11～14］，在不同位置、不同角度同时拍摄待测目标，适用于对实时性要求高的应用。通过上述两种方式获得目标图像后，能够完成目标空间三维信息恢复与重建。在实际应用中，可以对双摄像结构进行扩展，搭建多目立体视觉系统，提高获取信息的精度［15］。

本文搭建双目立体视觉系统，用以完成运动目标的空间定位。针对图像特征点定位误差影响目标空间定位结果的问题，提出了基于极线单应性的目标空间定位算法。

2 基于双目视觉的目标空间定位系统

2.1 系统结构

双目视觉系统的一般结构为交叉放置的两个摄像机，从不同角度观测同一被测物体，如图1所示。通过两个图像中对应点的图像坐标，可以根据几何原理求取空间点三维坐标。

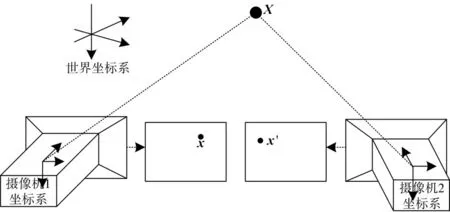
图1 双目视觉空间定位系统原理图

在双目视觉系统中，最常用的为平视双目立体系统。这时，两个摄像机的图像处于同一个平面上，即空间点在两个图像上的Y坐标相同。一般情况下，平视双目立体系统将两个成像单元集成到一个摄像机内，因此适用于对测量范围要求较小、对系统体积质量要求严格的场合。而当测量范围较大，并对测量精度要求较高时，比较适合采用如图1所示的基于双摄像机的双目立体视觉系统结构。

2.2 数学模型

图2 系统数学模型

图2 为基于双目立体视觉的目标空间定位系统的数学模型，左侧摄像机坐标系为，设为世界坐标系，其理想图像坐标系为同时，右侧摄像机坐标系为其理想图像坐标系为f1、f2分别表示两摄像机的焦距，α1、α2分别表示两摄像机光轴与基线lBL的夹角。假设空间点P在两摄像机光轴确定的平面上的投影点为P'，则ω1、ω2分别表示P'和两摄像机光学中心的连线与相应摄像机光轴之间的夹角，即P的水平投影角。假设P在两台摄像机下的坐标分别为(xp1,yp1)、(xp2,yp2)，由此可以推导出空间点P的空间三维坐标为

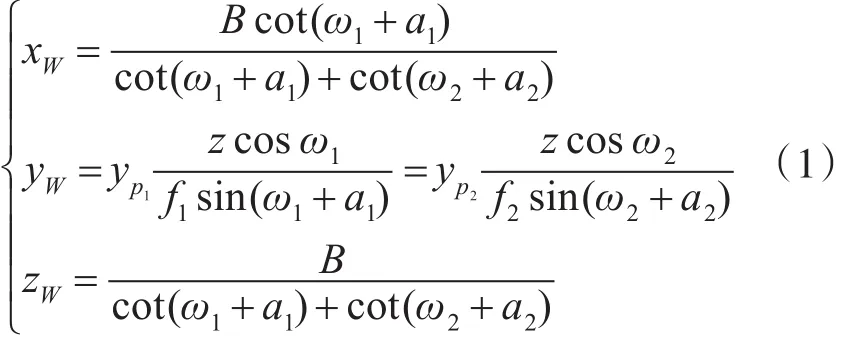
其中，ω1=arctan(xp1/f1)、ω2=arctan(xp2/f2)、z为物距、B为基线距。

3 基于极线单应性的目标空间定位算法

3.1 空间定位问题描述

在空间定位问题中，目标多由单个特征点进行表征。由此，空间定位问题简化为已知目标在两幅不同视角图像中的坐标为x、x'，已知摄像机矩阵分别为P、P'，且相对位置关系已知，求目标在空间中的三维坐标X。然而，在实际过程中，误差必然存在。为此，两个摄像机的光心与x、x'的连线可能出现偏斜，导致在空间中并不相交，即不存在三维空间点X满足对极约束条件，如图3所示。

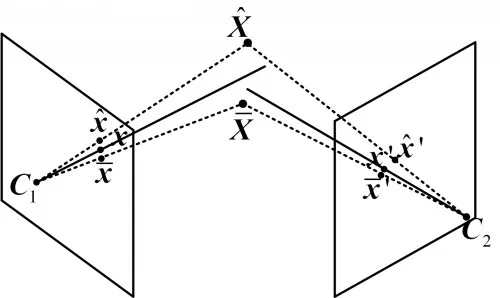
图3 特征点定位误差对定位系统的影响

目标的真实投影位置 xˉ、xˉ'由于误差产生了偏离。为此，上述问题可以转化为优化问题：

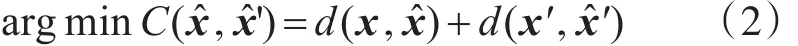
其中，C(xˆ,xˆ')为代价函数，两幅图像中对应点对xˆ 、xˆ'满足 xˆ'TFxˆ=0 ，d(⋅,⋅)表示两点之间的欧氏距离。因此满足式的xˆ、xˆ'与各自摄像机光心C1、C2所在直线必然交汇于空间某点 Xˆ，代价函数C(xˆ,xˆ')为 Xˆ的重投影误差。

3.2 算法原理及流程

针对式（2）的代价函数，提出了基于极线单应性的目标空间定位方法。在基于双目视觉的目标空间定位系统中，假设在某个摄像机图像中一条极线为l，与基线lBL共同确定一个平面π，该平面与C'摄像机的图像平面交于极线l'，由此可知双目视觉系统中极线存在单应性。

图4 基于极线单应性的空间定位原理

若空间点估计点Xˆ在摄像机1图像中的投影点位于极线l上，则对应点必然位于l所对应的极线l'上。显然，极线l、l'上的任意两点所组成的对应点对 xˆ、xˆ'均满足极线约束，即 xˆ'TFxˆ=0 。同理，x、x'在 l、l'上的投影点 x⊥、x'⊥同样满足极线约束，且当对应点位于极线l、l'上时，x⊥、x'⊥使得代价函数取得最小值。因此，代价函数可以转换为

通过变换极线对，可以获得最小化式3的x⊥、x'⊥，作为空间定位的图像估计点，从而得到目标点的空间坐标，计算方法如下：

将x=PX、x'=P'X转化为齐次方程AX=0，通过解齐次方程组，得到空间点X的空间坐标。由 x×(PX)=0、x'×(P'X)=0可以得到：

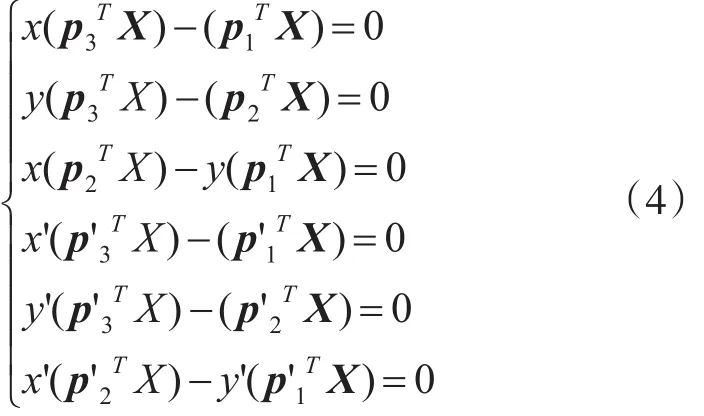
为简化计算，将目标的图像点x、x'平移至各自图像坐标系的原点，齐次坐标 x=(0,0,1)T、x'=(0,0,1)T，则极点e、e'的齐次坐标分别为e=(1,0,f)T、e'=(1,0,f')T。

由F(1,0,f)T=(1,0,f')F=0，可以得到基础矩阵的一般形式：

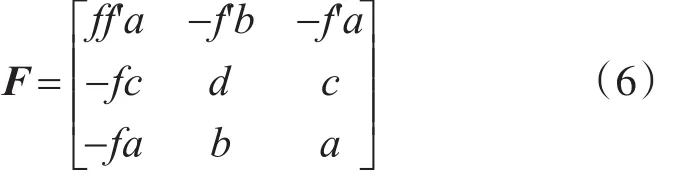
根据上述算法原理，基于极线单应性的目标空间定位算法流程如下：

1）将摄像机1图像上的所有极线参数化表示为 l(t)；假设极线 l(t)经过点 (0,t,1)T与极点(1,0,f)T，可以通过叉乘进行表示：

2）利用基础矩阵F计算摄像机2图像上对应的极线，并表示为l'(t')；

3）将代价函数表征为t的函数C(t)；

4）对t进行限制，求argmin(C(t))。

若要C(t)取到极小值，则有C'(t)=0。将式（10）进行通分，分子如式（11）所示：

g(t)为变量t的六次多项式，因此g(t)=0最多有6个实根。由于t→∞同样对应了图像中的一条极 线 ，还 需 将 C(t→∞)考 虑 在 内 。 令t=argmin(C(t))，其中t为g(t)=0的实根以及∞。

算法的具体实现过程如下：

1）构造平移矩阵T、T'，将图像上的目标点x=(x,y,1)、x'=(x',y',1)平移至各自的原点：其 中F=T'-TFT-1，更新后的F反映平移变换后的对应点位置关系；

3）构造旋转矩阵R、R'，使得Re=(1,0,e3)T、R'e'=(1,0,e'3)T；

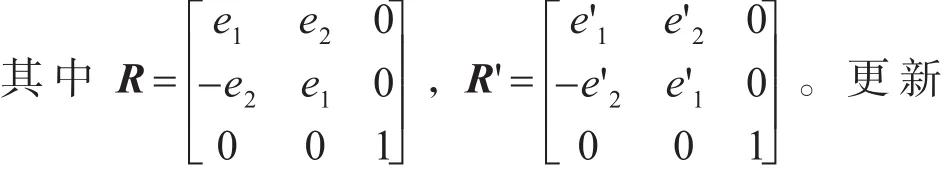
F=R'FRT，使得F满足式（6）的形式；

4）令 f=e3、f'=e'3、a=F33、b=F32、c=F23、d=F22，根据式（11）构造 g(t)，求得 g(t)=0的全部实数解；

5）将步骤4）中得到的实数解代入式（9）中，得到各自的代价函数值。计算

6）根据 tmin，得到 l=(tf,1,-t)，由式（8）计算得到l'；

7）根据 l、l'计算 xˆ⊥、xˆ'⊥：对于直线 (α,β,γ)，原点在其上的投影坐标为 (-αγ,-βγ,α2β2)；

8）还 原 xˆ⊥、xˆ'⊥至 平 移 旋 转 前 的 坐 标 系 ：xˆ =T-1RTxˆ⊥、xˆ'=T'-1R'Txˆ'⊥；

9）根据式（5）构造线性齐次方程组，求解对应空间点X的三维坐标。

4 实验及结果

实验平台搭建如下：摄像设备为XWJG-MV-U500工业摄像头，镜头分别采用XWJG-XG5100变焦镜头与XWJG-XG0412变焦镜头，焦距分别为5mm～100mm、4mm～12mm，定位目标为搭载GPS天线的SDI-W32H无人直升机平台。

目标真实位置信息由GPS定位设备获取，包括GPS接收机、数据发送终端和天线及安装固定装置等部分。基于载波相位的GPS差分定位精度可达厘米级，可以达到作为目标真实位置坐标的要求。

不同摄像机获得的部分视频图像如图5所示。

图5 部分实验测试集

两台摄像机的GPS坐标如表1所示。

表1 摄像机GPS坐标

实验获得无人机GPS坐标，部分数据如表2所示。

表2 无人机GPS坐标

将表3数据转换为空间直角坐标，并将坐标系原点移至1号摄像机，结果如表3所示。

表3 转换后坐标

表3数据所表征的无人机的部分飞行轨迹如图6所示。

图6 无人机空间真值轨迹

为了突出算法的实现过程，将获得实验图像的无人机区域进行显示，如图7所示：图中灰色极线对应另一视角下无人机红色质心点，黑色极线为本章定位算法计算所得，质心点在黑线上的投影点（绿点）为算法得到的满足 xˆ'TFxˆ=0的对应点。

实验引入了中点式定位方法和鲁棒的近似极大似然定位方法（Robust Approximate Maximum Likelihood：RAML）作为对比算法，在系统结构不同设定条件下，得到的定位误差如图8所示。

图7 对应点匹配结果图

由图8所示，本章提出的基于极线单应性的目标空间定位算法在任意系统结构下均具有更高的定位精度，但是当基线距离减小时，定位误差明显增大；而当选用小焦距镜头时，系统的定位误差急剧增加，实验得到的平均定位误差如表4所示，可知，当基线距为20m、镜头焦距为100mm，物距为100m左右时，运动目标空间定位的平均误差达到0.251m，具有较高的精度。

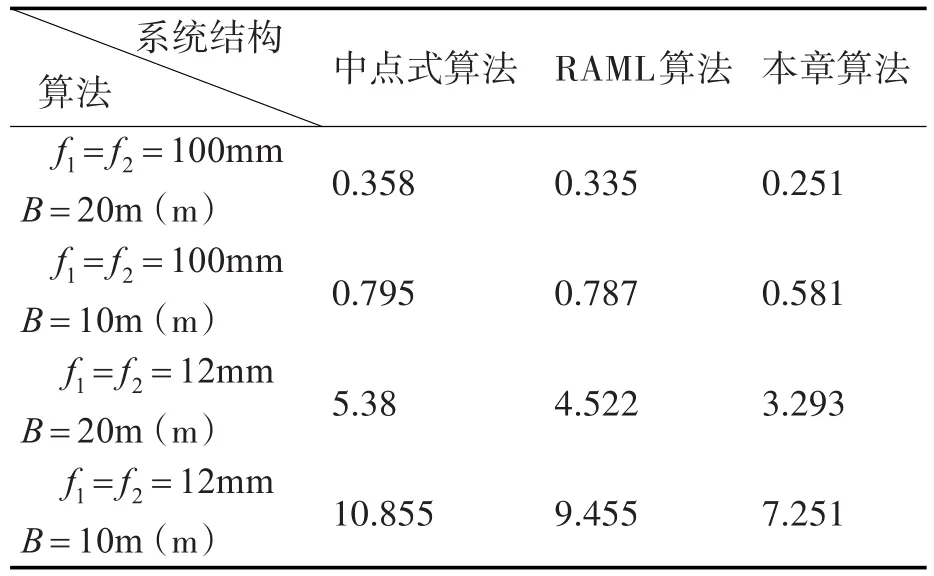
表4 定位误差表

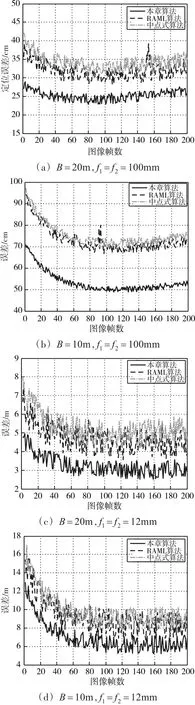
图8 空间定位算法误差

5 结语

本文首先阐述了基于双目立体视觉的目标空间定位系统结构与数学模型。针对特征点定位误差对空间定位算法产生的不利影响，提出了基于极线单应性的空间定位算法。实验将SDI-W32H无人直升机平台作为目标，将差分GPS设备得到的相对位置信息转换为目标的空间坐标，并将其作为真值。

实验结果表明基于极线单应性的空间定位算法在基线距为20m、镜头焦距为100mm，物距为100m左右时的平均误差能够达到0.251m。另外，在各种系统结构下，本章算法较中点式和RAML算法，精度均得到了较大的提高。