数控机床的热误差补偿技术研究

陈建国，方 辉

（1.成都农业科技职业学院 机电技术分院，四川 成都 611130；2.四川大学 制造科学与工程学院，四川 成都 610065）

1 引言

农机生产中热误差是影响数控机床加工精度的一个主要误差源[1]，热误差主要由内、外部热源引起，内部热源主要有机床加工与切削，例如主轴电机、轴承摩擦等[2]；外部热源则是周围环境，例如：相邻机械热量、环境温度变化等[3]。众多的研究表明[4]，数控机床的所有定位误差中热误差高达75%，而主轴热变形是热误差的最主要因素。

针对热误差的解决方案主要有：热稳定性材料[5]与热误差补偿方案[6]。热稳定材料使用纤维强化的材料来降低数控机床的热变形，具有较好的效果，但其经济成本极高，且容易导致机床震动加剧与加速度降低等问题。热误差补偿方案则通过数值补偿来降低热误差，热误差补偿的经济成本较低，并且可兼容不同的热误差源，具有较好的适应能力。

现有的热误差补偿模型主要有统计回归建模[7]与神经网络建模两种方式[8]，统计回归建模具有成本低，但其精度不足。而神经网络能以任意精度逼近任意非线性映射，可获得较高的精度，但神经网络需要采集大量的数据来进行模型训练，建模成本较高且需要安装较多的传感器，所以实际应用的建模成本较高。国内外的研究人员针对神经网络建模的优缺点提出了众多的改进策略：文献[9]提出一种基于粒子群算法的温度测点优选方法和基于极限学习机神经网络的机床热误差补偿模型，该补偿模型具有计算简便、预测精度高、结构简单等优点。文献[10]提出了将主成分分析与BP神经网络相结合的主轴热漂移误差的建模和预测方法。目前改进的神经网络建模方法主要通过排序或聚类算法减少测点的数量，从而降低建模成本，但同时也导致了预测精度的降低。

针对上述问题，设计了改进的神经模糊网络建模方案，采用灰色理论过滤不利的输入变量，有效地提高了神经网络的训练效率与精度。机械实验结果表明，热误差补偿模型的预测精度高于其他模型，并具备较好的鲁棒性。

2 自适应神经模糊系统

自适应神经模糊推理系统（ANFIS）具有直接通过模糊推理实现输入层与输出层之间非线性映射的能力，以及神经网络的信息存储和学习能力。模糊推理系统中一般通过试错法调节隶属函数，而FIS则探索如何获得模型的目标。另外通过ANN技术从一个训练数据集学习并建立模糊模型的参数，并映射为模糊模型的解（可使用“IF-THEN”规则）。

2.1 ANFIS架构

ANFIS的模型架构，共包含5层。每层的节点通过节点函数描述，方形表示自适应节点，其参数集为可调节，圆形表示固定节点，其参数集为固定值，如图1所示。为了简化分析，假设ANFIS具有两个输入变量（T1，T2）与一个输出（F：热漂移）。

图1 ANFIS的模型架构Fig.1 The Model Structure of ANFIS

第一层（模糊层）：通过隶属函数将输入转化为一个模糊集，包含自适应的节点，节点函数为：

式中：T1与 T2—输入节点 i；A 与 B—节点的标记；μ（T1）与 μ（T2）—隶属度函数。采用最大、最小值分别为1与0的高斯型函数作为隶属函数。

第二层：第二层的节点为固定节点，表示为圆形，标记为∏，将输入信号乘以节点函数获得输出信号：

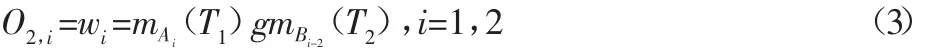
式中：O2，i—第二层的输出，输出信号wi表示规则的启动强度。

第三层：第三层的节点为固定节点，表示为圆形，标记为N，节点函数将启动强度归一化处理，计算第i个节点的启动强度与所有启动强度的比例。

式中：O3，i—第三层的输出；w—归一化的启动强度。

第四层：第四层的节点为可调节节点，表示为方形，节点函数定义为：

式中：f1与f2—模糊规则，分别定义如下：

式中：pi，qi，ri—参数集合。

第五层：第五层的节点为固定节点，表示为圆形，标记为Σ，节点函数定义为：

最简单的ANFIS学习规则是“后向传播”，递归地从输出层计算误差信号。

2.2 初始化模糊模型的提取

首先推导初始化的模糊模型，初始化模型需要选择输入变量、输入空间分类、隶属度函数的数量与类型，并创建模糊规则。一个给定的数据集使用不同的识别方法可能产生不同的ANFIS模型，例如：网格分区与模糊c-means聚类算法。

为了减少模糊规则数量，使用ANFIS与FCM聚类算法结合的模糊规则生成方案，FCM用来识别ANFIS模型系统的模糊MF与模糊规则。

2.3 模糊c-means（FCM）聚类

FCM为软聚类方法，每个数据点根据隶属度值属于一个类簇，FCM的优点是允许同一个数据不单独地属于一个分类，而是可以出现在中间。

假设将长度 n 的向量 xi（i=1，2，...，n）进行模糊分组，i=1，2，...，c是被选择的n个点。FCM的处理步骤主要为：

第一步，从 n 个数据模式｛x1，x2，x3，…，xn｝中随机地选择每个类簇ci的中心；

式中：μij—类簇i中对象j的隶属度；M—范围［1，∞］序号的模糊指数；dij=||ci-xj||—ci与 xj的欧式距离。

第四步：c模糊类簇的新中心 ci（i=1，2，…，c）计算为：ci=

采用FCM算法将训练数据分为几个子集，然后使用ANFIS训练各子集，此外，通过FCM算法搜索热误差补偿模型的最优温度数据分簇。

3 输入变量的选择

过多的热传感器可能对热预测模型的精度与鲁棒性产生负面的影响，为温度传感器选择合适的位置是一个关键的问题，采用灰色理论为热误差模型选择合适的传感器位置。灰色理论最重要的优点是仅需要少量的实验数据，即可获得精确的预测，使用一阶灰色模型GM（1，N）。

一阶灰色模型GM（1，N）是多变量灰色模型。GM（1，N）表示一个有N个变量的灰色模型，其中包含一个因变量与N-1个自变量。假设共有N个变量，xi（i=1，2，...，N），每个变量有n个初始化序列：

首先，为了降低序列的随机性、增加序列的平滑度，使用累加运算将序列转化为单调增序列。为了简化分析，定义的一阶k=1，2，…，n。

然后，将GM（1，N）模型表示为以下的灰色差分方程：

式中：系数a与bj—系统的开发参数与推导参数。

从（10）式可获得下式：

可将（5）式改写为以下的矩阵形式：

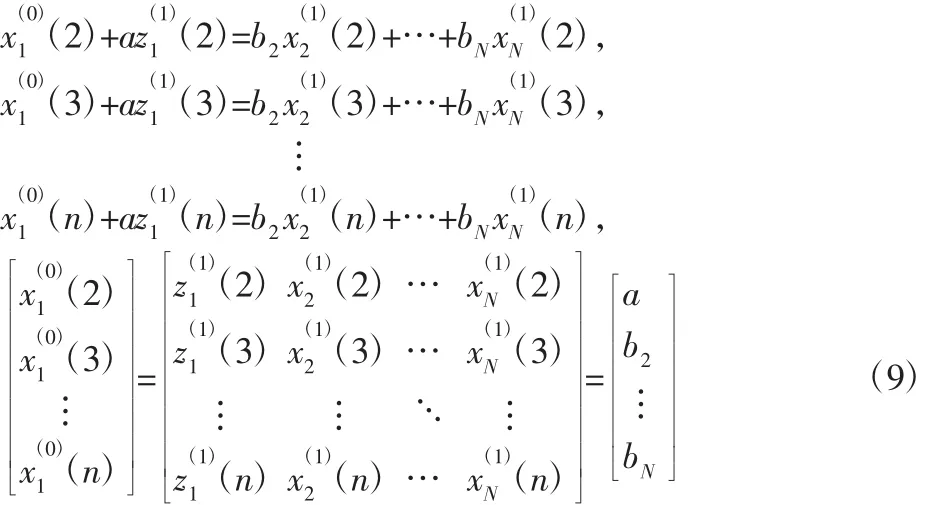
使用最小二乘估计法计算模型的系数：

因此，通过比较模型的（b2～bN）值可获得从自变量到因变量的影响度。

为了增强模型的鲁棒性，使用FCM将所有热传感器的影响度权重进行分组；然后，从每个类簇选择一个传感器来代表该类温度传感器来预测热漂移。因此，仅通过5个传感器尽可建立一个简单的ANFIS模型来预测热漂移。

系统的框图，如图2所示。图中：变量（T1～TN）—温度传感器采集的数据。

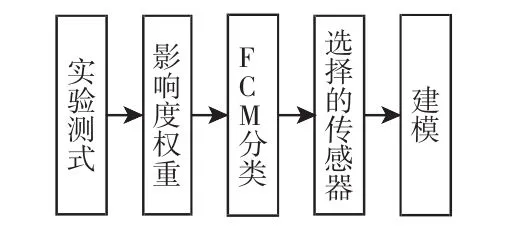
图2 系统模型的框图Fig.2 The Diagram of the Proposed System Model

4 实验结果与分析

4.1 测量系统的建立

三轴顶点立式铁床机床的框图，如图3所示。主轴电机通过每个端点的轴承直接与机床滚珠丝杠耦合。主轴托架的顶部为一个DC电动机，控制主轴的旋转，主轴速度范围为（60～8000）r/min。为了获得机床的温度数据，共设置了76个热传感器。

机床的环境与操作不断变化，极少保持稳定状态，设置了5个非接触式位移传感器测量精密测试棒的位移（XYZ轴）。实验设置为两个小时，第一个小时为加热，后一个小时为冷却，主轴转速为8000r/min。主轴在三个方向的漂移位移变化，X轴的最大位移为3μm，Y轴为79μm，Z轴为22μm，如图4所示。因为机械的对称性，所以X轴的热偏移小于Y轴与Z轴，所以仅Y轴与Z轴的误差。

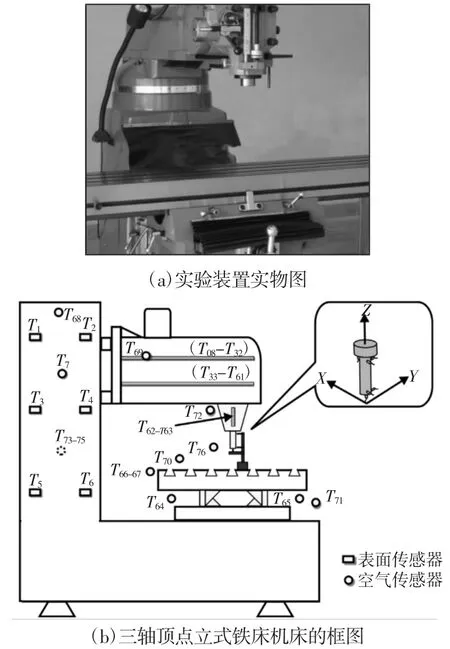
图3 实验场景Fig.3 The Experimental Scenario

图4 主轴在三个方向的漂移位移变化Fig.4 The Displacement Variety of Drift in Three Directions for Principal Axis

4.2 不同关键点传感器的影响权重

温度变量的选择是热误差模型精度的一个关键因素，如果输入的变量数较多，则校准、训练时间与相应的系统成本将增加，所以在建模之前应当决定合适的温度传感器位置。使用灰色模型GM（1，N）对上述测试例进行分析：

假设 T1～T76代表自变量（输入），主轴传感器的Y轴测量值是目标变量（输出）。影响度权重越大，则对热误差的影响越大。使用FCM聚类将影响度权重分为5类结果，如表1所示。从每个类簇根据其影响度权重选择一个传感器来表示同一类的温度传感器，选择 T18、T55、T63、T68与 T71。

表1 使用FCM对影响度权重的分类结果Tab.1 The Results of Impact Weights Classified by FCM

4.3 实验结果与分析

使用ANFIS模型推导热误差补偿系统，训练数据集的数据实验为：实验设置为两个小时，第一个小时为加热，后一个小时为冷却，主轴转速为4000rpm；测试数据集为上文的数据。使用三个性能指标计算模型的性能，分别为根均方误差与相关系数。

4.3.1 相同主轴转速的预测效果

使用训练数据集建立预测模型，测试数据集实验为5h，前3h为加热，后2h为冷却，主轴转速为4000r/min。使用预测模型预测上述测试数据集的热误差。最终根均方误差为0.99，相关系数为1.06。预测模型与实际实验的热偏移曲线，结果显示本预测模型预测的预测量，精度较高，如图5所示。

图5 预测模型与实际的热偏移的曲线Fig.5 The Curves of the Proposed Prediction Model and the Practical Thermal Migration

4.3.2 不同主轴转速的预测效果

使用训练数据集作为训练集，第一组实验的8000r/min转速数据集作为测试集。最终根均方误差为0.99，相关系数为2.78。预测模型与实际实验的热偏移曲线，结果显示本预测模型预测的预测量，精度较高，如图6所示。

图6 预测模型与实际的热偏移的曲线Fig.6 The Curves of the Proposed Prediction Model and the Practical Thermal Migration

5 结论

农机生产中热误差是影响数控机床加工精度的一个主要误差源，基于神经模糊系统设计了农用机械数控机床的热误差补偿模型。设计了改进的神经模糊网络建模方案，采用灰色理论过滤不利的输入变量，有效地提高了神经网络的训练效率与精度。机械实验结果表明，热误差补偿模型的预测精度较高，并具备较好的鲁棒性。