人均生活用能变化规律及数学建模

☉清华大学附属中学 侯陈隽

一、问题的提出

能源是人类生存和发展的重要基础.我们日常家庭生活中使用的电灯、洗衣机、冰箱、空调等要消耗电，做饭烧水要消耗天然气等.我们的生活用能变化蕴含着怎样的变化规律？如何建立数学模型来反映这些规律并进行预测？

二、数据收集处理

从“中国经济与社会发展统计数据库”（http：∥tongji.cnki.net/）上获得1990-2015年居民生活用能情况.由于获得的液化石油气、天然气、煤气的消耗量单位不同，因此按照这3种气体大致的热值12 000Kcal/kg、8500Kcal/m3、3500Kcal/m3计算得到总用气量，处理后的数据见表1（为减少篇幅，表1仅列出了每5年的数据，本文数学建模用了25年数据）.

继续查询了1990-2015年城镇与农村居民人均收入、城镇人口比重数据.统计数据中关于人均收入给出了两个值，一是当年价的人均收入，二是相对于1978年的指数.由于货币量指标涉及价格问题，不同年份间的货币量为了可比较需要剔除由于通货膨胀等引起的价格变化因素.因此根据下面计算式计算出全国居民以2015年价格计算的人均收入It，结果如表2所示（同样为减少篇幅仅给出每5年的数据）.

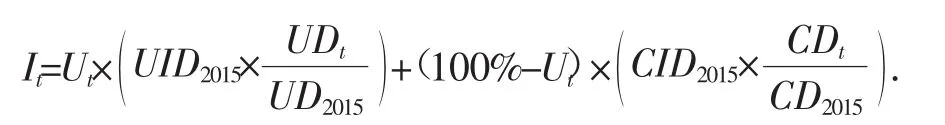
其中Ut表示t年城市人口比重，UIDt、CIDt分别表示城镇与农村居民t年的当年价人均收入，UDt、CDt分别表示城镇与农村居民t年人均收入相对于1978年的指数.

三、模型建立

1.人均生活用能变化规律

为了探究人均生活用能的变化规律，将上述处理过的分类用能数据与人均收入数据用Excel画图显示，见图1，其中的散点是统计数据，曲线与直线分别用多项式函数和线性函数拟合.

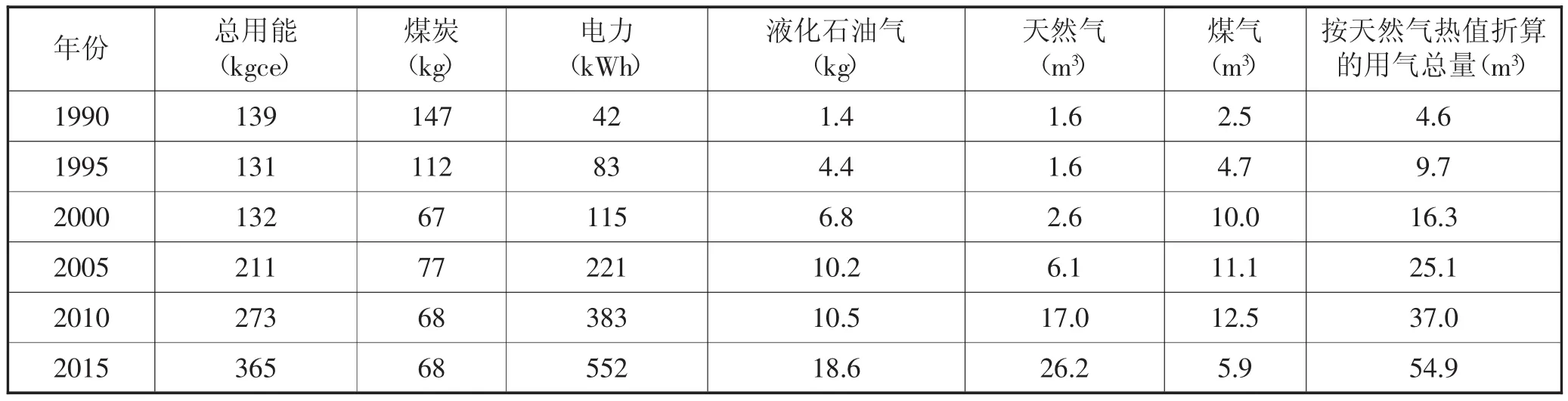
表1 1990-2015年人均生活用能数据

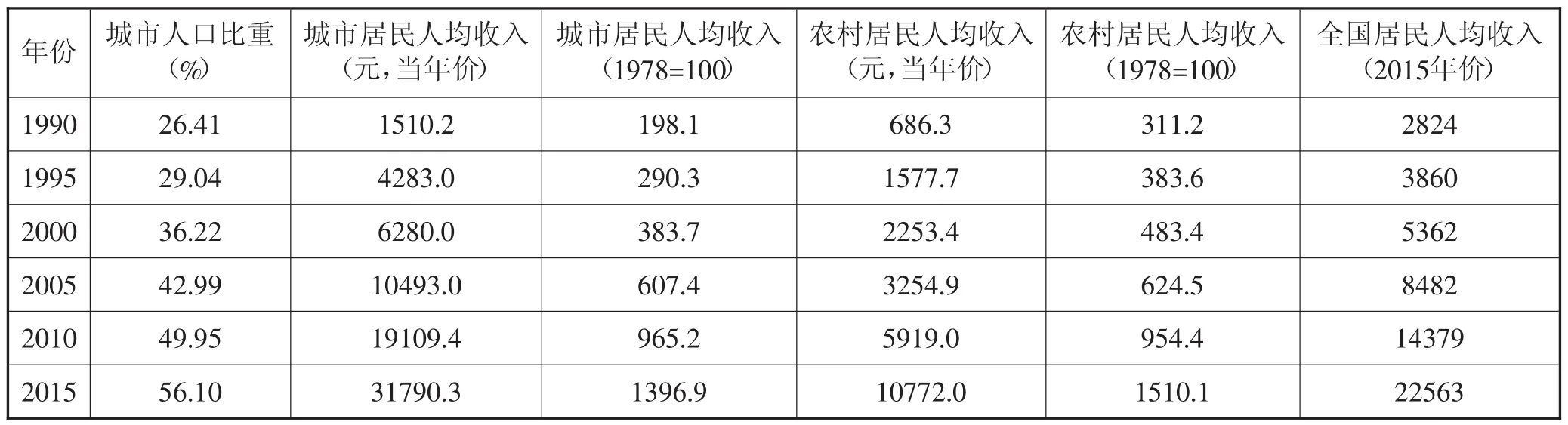
表2 1990-2015年人均收入数据

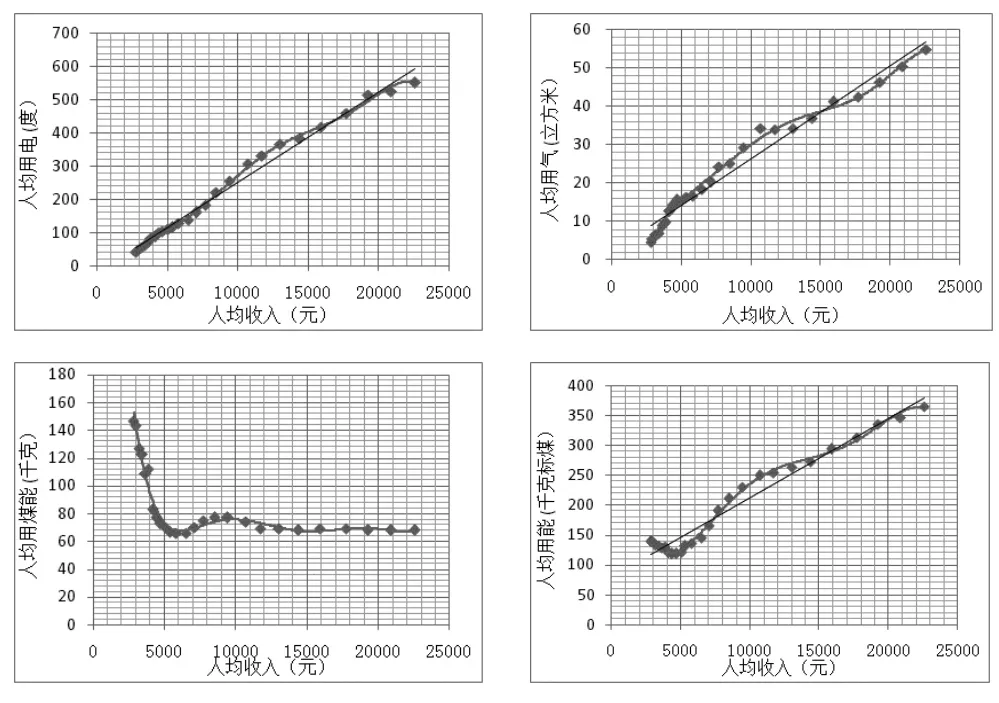
图1 人均生活用能（电、气、煤）随人均收入变化的规律

多项式函数可以较好地描述已有的统计数据间的数学关系，但是我们建立人均生活用能数学模型的一个重要目的是预测未来人均收入进一步提高后的人均生活用能情况，而多项式数学模型将使得当人均收入达到25000元时人均生活用电量及人均生活总用能量都呈下降趋势，与现实不符，故不宜使用.

人均生活用电与用气量均随人均收入的增加而增加，而且大致可以用线性函数进行描述.在人均收入5000元之前，人均用电与用气量都很低，煤炭是主要的生活燃料.但煤炭燃烧会造成严重的大气污染与室内污染，危害居民身体健康.随着人均收入的提高，一方面居民有能力选择价格更高的清洁能源，另一方面居民的健康与环境保护意识加强，因此人均用煤量不断下降.当人均收入低于5000元时，由于人均用煤量的降低，人均生活总用能也呈下降趋势；当人均收入高于5000元时，人均生活总用能随人均收入的提高而增加，而且也大致呈线性关系.

2.线性函数模型

设t年的人均收入为自变量xt，人均生活用能（或人均用煤量或人均用电量或人均用气量）为因变量yt，若x与y之间存在近似的线性相关关系，则可以用下面的回归直线方程来表示这种关系：

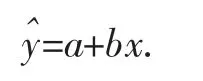
为使得回归值与统计值间全部误差的平方和达到最小，系数a和b的计算公式如下：

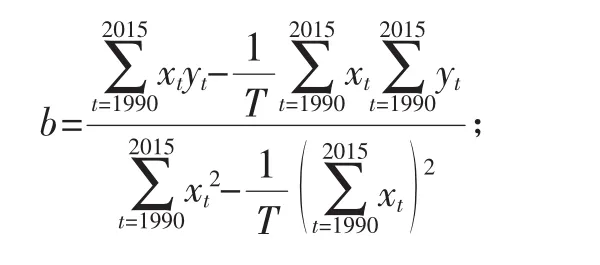
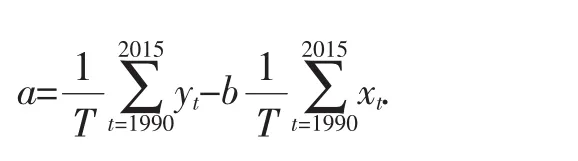
检验变量x与y相关关系的统计量相关系数R的计算公式如下：

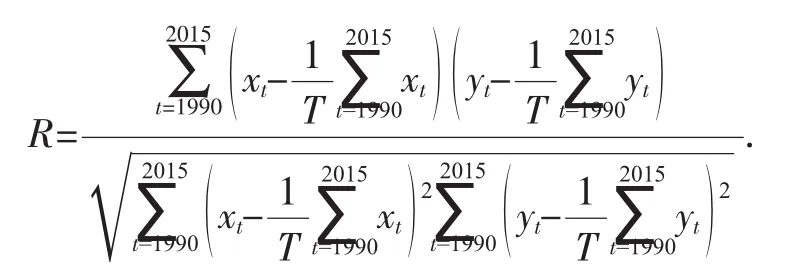
其中T为25.

应用上述计算式可以求得人均生活用电量与人均收入的相关系数R为0.99，R非常接近于1，说明线性相关程度非常强.在《高中数学选修2-3》附表中可以查到R0.01为0.505，R>R0.01，因此有99%的把握认为人均收入与人均生活用电量之间具有线性关系，建立的线性函数模型如下：

ELEt=0.027It-23.8.

其中ELEt为人均用电，It为人均收入.该线性函数的斜率表明人均收入每增加1千元，人均用电将增加27度.

同样可以求得人均生活用气量与人均收入的相关系数R为0.98，人均生活用电量与人均收入间的线性函数模型如下：

GASt=0.002It+2.172.

其中GASt为人均用电，It为人均收入.该线性函数的斜率表明人均收入每增加1千元，人均用气每年将增加2m3.

用相同的方法可以得到当人均收入低于5000元时人均生活用煤量与人均收入的相关系数R为0.98，人均生活用煤量与人均收入间的数学模型可表示为：

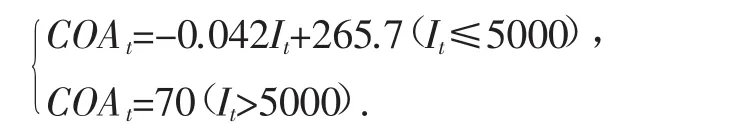
其中COAt为人均用煤，It为人均收入.当人均收入低于5000元时，人均收入每增加1千元，人均用煤量每年将下降42kg；当人均收入高于5000元后人均煤炭的使用量大致稳定在70kg左右.若要进一步下降煤炭消费量，政府需要加强电网、天然气管道的建设，使得更多的居民在收入提高后可以获取清洁的能源而不再使用煤炭.

用相同的方法可以求得人均生活总用能量与人均收入的相关系数R为0.98，人均生活用气量与人均收入间的线性函数模型为：

ENEt=0.013It+79.79.

其中ENEt为人均生活总用能，It为人均收入.人均收入每增加1千元，每年人均生活总用能将增加13kgce.

四、模型的改进与应用

应用上述线性函数模型可以预测未来的人均生活用能情况.例如，当人均收入增加至30000元时，人均生活总用能、人均生活用电量、人均生活用气量将分别增加到470kgce左右、786度、62m3左右.当人均收入达到1.5万美元即10万元时，人均生活总用能、人均生活用电将达到1380kgce、2676kWh左右.而英国当前人均收入约是我国居民的10倍左右，其人均生活总用能、人均生活用电仅分别为800kgce、2000kWh.因此需要对线性函数模型进行改进，以反映我国大力提倡的节能减排政策.

考虑到人均生活用能不能随人均收入的增长而持续增长，应该控制在一个合理的水平之下，因此应用如下的函数形式建立数学模型：

ENEt=ENE0eαeβIt，

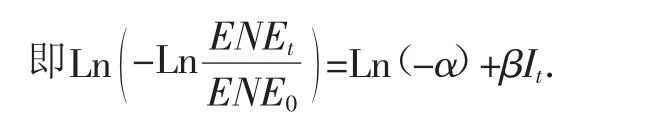
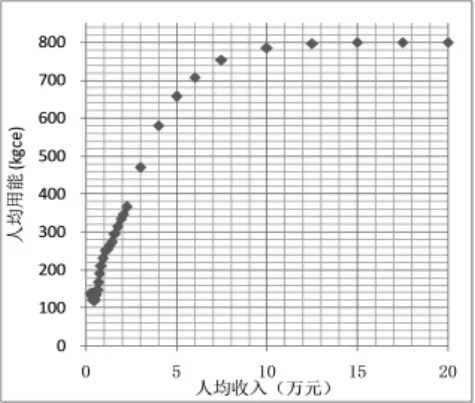
图2 应用分段数学建模对人均生活用能的预测

应用此模型预测得到的人均收入10万元时的人均生活总用能为785kgce，在人均收入达到12.5万之后人均生活总用能维持在800kgce左右.

若假设当前英国居民的人均生活用电量2000KWh为合理生活用电控制水平，以为纵坐标，It为横坐标作图，拟合的曲线也呈线性关系，计算的相关系数R为0.97，α，β分别为-3.904、-5.63E-5.取收入60000元作为两个模型预测的分段点预测的人均生活用电结果见图3，改进后的模型可以表示为：

应用该模型可预测当人均收入达到10万元后人均生活用电大致维持在2000kWh.

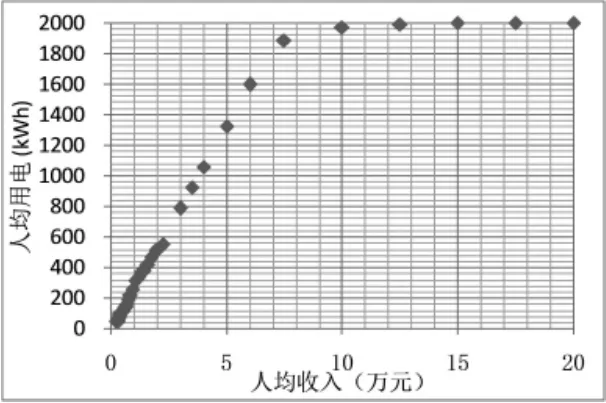
图3 应用分段数学建模对人均生活用电的预测

五、结论

在一定的收入水平范围内，人均生活用能（用电、用气）与人均收入成线性相关，可以建立线性函数模型预测人均收入一定增长后的人均生活用能（用电、用气）；当人均收入几倍甚至几十倍于拟合所采用的统计值时，应该考虑采用合理控制水平的数学模型.这种建立线性函数模型与考虑合理控制水平数学模型相结合进行分段预测的方法可以推广适用于其他方面，比如户均空调拥有量的预测等.