智能手机多传感器融合的实时定位算法

崔思柱，刘丰豪，程石，肖倩

（长安大学工程机械学院，西安 710064）

0 引言

现代智能手机配置了各类传感器，包括全球卫星定位系统GPS（Global Position System）、加速度计、角速度计、气压计及多个摄像头等，这些配置使手机能够通过多种方式获得当前的位姿信息[1]。主流的定位方式仍是通过GPS，但是复杂环境中会存在弱GPS甚至无GPS信号的地方，例如密集的建筑群街道、室内、野外丛林等，此时GPS信号无法满足精确定位要求。因此需要采用新的方式来进行实时定位以获取实时位姿信息。

目前跟踪定位方式主要有两种，一是基于视觉传感器的姿态跟踪方式，二是基于惯性传感器的姿态跟踪方式。前者通过对视觉传感器获得的图像进行特征提取、特征匹配、三角化、PNP、最小化重投影误差，计算出传感器的位置，通过坐标变换进而获得搭载传感器的物体瞬时位置和姿态。具有实时、非接触等优点，但受到光照强度，运动速度的限制。基于惯性传感器的跟踪系统中，采集原始数据的硬件为陀螺仪和加速度仪。通过陀螺仪采集的角速度和加速度计采集的加速度信息，将两者对时间进行积分可以粗略获得搭载惯性传感器物体的姿态。由于惯性传感器的输出频率较高，在快速运动时仍然适用，物体外观和外界环境变化对计算结果不会产生影响。受噪声及其自身偏差影响，惯性传感器数据误差会随时间逐渐累积，其准确率也会随之下降，所以只能适应短时间精确定位要求。本文提出融合视觉和惯性测量系统的方案，结合上述两种定位方式的优点以获取更加精确的位姿。该方案流程如图1所示。

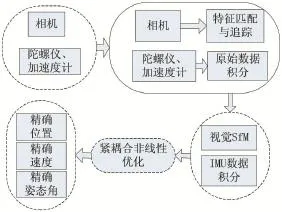
图1 传感器融合定位方式流程图

1 理论基础及模型建立

1.1坐标系定义

相机坐标系{C}：目前智能手机相机模型通常是针孔模型，本文通过将模型中心作为原点建立三维相机坐标系。以相机的光轴作为坐标系的Z轴，对应坐标轴Xc、Yc与图像物理坐标系平行。

图像坐标系{P}：图像像素坐标系以图像左上角为坐标原点，横坐标u和纵坐标v分别是图像所在的行和列；图像物理坐标系以图像的中心为原点，坐标轴X和Y分别与像素坐标系的u,v对应[2]。

惯性坐标系{I}：惯性坐标系的Zi轴与相机坐标系的 Zc轴平行且方向相反，Xi、Yi与相机坐标系 Xc、Yc成90°夹角，原点位于相机坐标系原点的正下方。当相机固定在机器人或其他设备上时，惯性坐标系即默认为运动载体的体坐标系。

世界坐标系{W}：全局坐标系选取具有任意性，本文设定Zw垂直向上，将前进方向设定为Xw正方向，通过右手坐标系规则即可确定Yw方向。具体关系如图2所示。

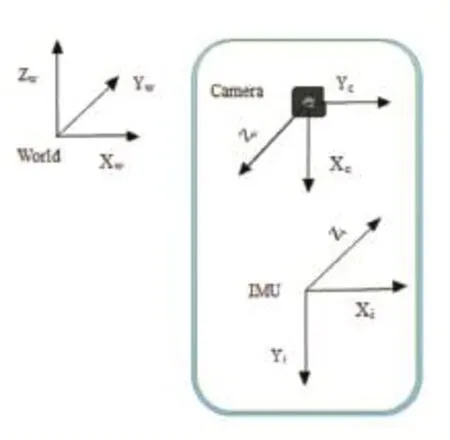
图2 智能手机相关坐标系

1.2前端数据处理

（1）视觉前端处理

采集图像的视觉传感器设备为智能手机携带的后置相机，常规后置相机像素通常为800万或1500万，性能优异的高端机可达到2000万。对于具有实时要求的定位系统而言，计算量将会显著增加。选取合适的特征处理方式对于提高位姿估计精度十分重要。

位姿估计过程中，对图像进行特征提取是前端处理的重要部分，特征提取的精确性和稳定会显著影响位姿估计。如果在视觉传感器采集的原始图像中选中某些具体的物体作为特征，将无法适应复杂多变的环境，而通过选定图像中简单、明显的点特征，不仅能够增强系统适应性而且会减小计算量。对于特征点处理分为以下步骤，检测、提取、匹配、剔除离群点，目前视觉导航中对于特征提取算法有Harris角点，David G.Lowe提出的SIFT算法[3]以及Herbert Bay等人提出的SURF算法[4]等。SURF基于积分图像提取特征点，通过Haar小波滤波器描述特征点，是一种集特征提取和描述于一体的算法，具有尺度不变性[5]。其抗干扰能力强，运算量低于SIFT算法，运算速度却更快，并且结合了SIFT算法的许多优点[6]。考虑到智能手机像素通常较高，因此选用SURF算法进行图像的特征处理。

前端处理需要首先对特征点进行高斯滤波，构建Hessian矩阵并建立图像的尺度空间，利用非极大值抑制方式选择特征点并精确定位，计算得到每个特征点的主方向，并构造SURF特征点描述子。最后通过判定最近邻欧氏距离和次近邻欧氏距离的比值是否小于设定阈值，进行特征匹配。通常SURF特征匹配会存在误匹配的现象，本文通过RANSAC算法剔除离群点，以消除误匹配带来的影响。如图3所示。

图3 实验场景特征点匹配

（2）惯性传感器前端处理

实时定位系统中使用关键帧技术能够减小后端非线性优化求解器的计算量，然而IMU数据输出频率通常比视觉传感器输出频率高很多。例如本文使用的小米智能手机，相机帧率约23Hz，惯性传感器频率约200Hz。通过对两帧图像间隔内的IMU数据积分成相对运动进而抑制优化变量的快速增长，避免当姿态变化时重新传输IMU数据，实现实时优化。

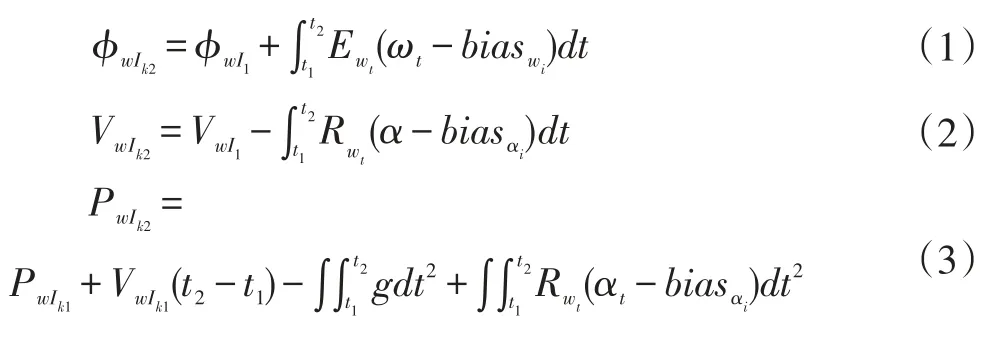
t1、t2为相邻时间间隔，P、V、φ分别为惯性坐标系相对全局坐标系的位置、速度、旋转矩阵。

对于IMU的状态传输需要惯性坐标系和世界坐标系之间的变换，这个全局旋转矩阵的求解需要已知初始姿态。如果将整个系统的参考坐标转变为初始坐标系I0，并且在IMU传输过程中转变为Ik，则可对公式中与加速度和陀螺仪相关的部分进行积分。

2 传感器融合及优化

2.1初始化

单目相机具有尺度不确定性，如果没有良好的初始估计值很难直接融合视觉和IMU测量值。通常会采用平稳假设，前几秒IMU测量值的平均值作为重力向量，但是当IMU测量值受到偏置影响，或在初始时刻出现加速运动，这种假设不成立。该融合算法中采用松耦合传感器融合的方式来得到初始值，通过五点法或八点法，得到位姿的初始估计值（旋转矩阵、平移向量）。将IMU预积分与视觉SfM结果对齐，可粗略地恢复尺度、重力、速度、加速度计和陀螺仪的偏置[7]。

首先，检测相邻两帧对应的特征，如果特征数量超过35个，平均视差超过了25像素，通过八点法恢复相邻两帧间的旋转矩阵和平移向量。固定平移矩阵的尺度并三角化两帧间所有观测特征。基于三角化的特征，采用PnP方式估计其他帧的位姿。最后通过Bundle Adjustment方式最小化所有观测特征的重投影误差[8]。

设定第一个相机坐标作为基准坐标系，所有特征的位置和姿态对于该坐标系。假定已知相机和IMU的外参,则可以将所有以相机为基准的位姿转为以IMU为基准的位姿。

通过最小化所有IMU和视觉测量值误差的范数之和，即求解最小二乘问题，实现对该系统的初始化。

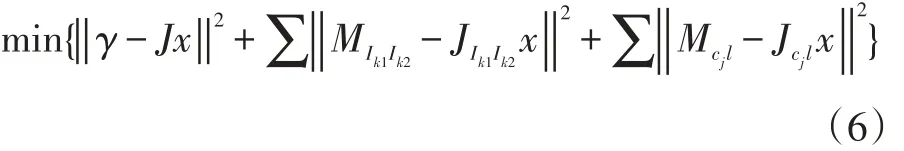
{γ，J}为先验值。MI，Mcjl分别对应 IMU 和视觉测量值模型，前者通过预积分公式（1）～（3）可求得，后者为第i帧中特征点的像素值对应的第j帧中第l个特征点的观测值。雅克比矩阵JI，Jcj分别对应测量值模型MI，Mc对状态量 x的偏导。

2.2紧耦合非线性优化

初始化后，为了得到更加精确的状态估计值，需要对初始化结果进行优化处理。定义状态向量为：

TIc为相机和IMU的外参。xk为第k帧对应的状态量，包括位置、速度、方向以及偏置。最小化先验值和所有测量值残差的马氏范数之和，以得到最大后验估计值。

两个连续帧间的IMU测量值残差。

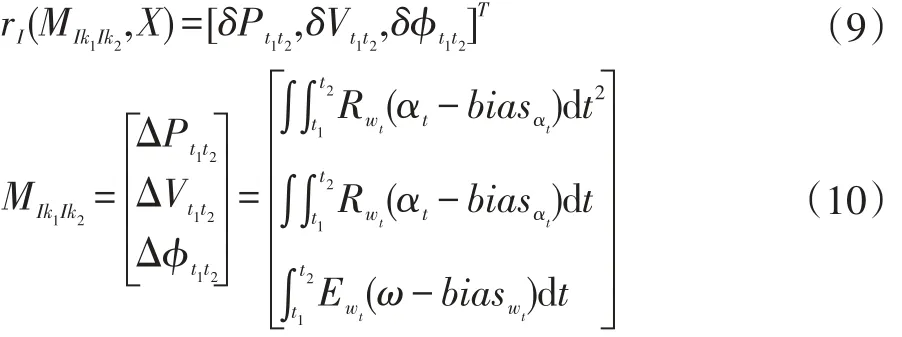
两个相邻关键帧的视觉测量值残差，即重投影误差，[Fx，Fy，Fz]为对 i帧中第 l个特征点进行反投影得到特征点，通过相关变换求得j帧中相对应的特征点的空间坐标。[u，v]为j帧中第l个特征点对应的归一化坐标。

3 实验结果及数据分析

实验中手持小米note智能手机进行实验。实验环境为室内走廊，走廊中线即行走路径，大小为14.4m×5.6m。实验结果如图4，红线为行走路线，蓝线为测量轨迹，以实验区域外1.5m处为起始点，红圈为设定终点（1.5,0,0），实际测量轨迹终点为（2.1044,-0.3480,0.1128）。设定实验总长度为42m，实际轨迹长度为44.98m。Z轴在整个实验过程随时间累积误差为0.1128m。试验中经过了三次转弯，起始端和设定轨迹基本重合，第一次转弯后出现明显方向偏差，随后分离程度增大。

实验结果可知随着时间增加定位精度会下降，同时姿态角多次变化也会降低定位精度。

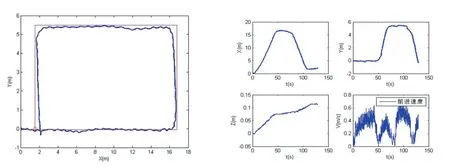
图4 室内走廊实验