方向关系在空间查询中的应用研究

王中辉，孙 立，禄小敏，徐智邦

（1. 兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070；2. 甘肃省地理国情监测工程实验室，甘肃 兰州 730070）

0 引 言

空间方向关系是人们描述、表达地理空间必须要面对和研究的基本空间关系之一。空间方向关系作为空间查询的重要选取条件，在空间数据挖掘和地理信息系统等许多空间信息科学领域得到了广泛的应用[1-5]。

目前，学者们对基于拓扑、距离关系的空间查询研究已经比较成熟；而对基于方向关系的空间查询研究却相对滞后[2]。文献[1]利用矩形模型和R树索引实现了基于方向关系的空间查询，但由于矩形模型自身存在的缺陷，导致查询结果在许多情况下出现错误；文献[2-3]利用方向关系矩阵模型和R树索引研究了基于方向关系的空间查询，但该算法只能处理八方向的空间查询；文献[4]借助平面扫描技术提出了一种高效的基于方向关系的空间查询算法，但该算法的查询对象仅限于互不相交的矩形。

鉴于此，本文对方向关系在空间查询中的应用进行了研究。在分析和比较现有空间方向关系计算模型及空间索引的基础上，利用锥形模型和四叉树索引，提出了一种基于方向关系的空间查询算法；并进一步结合空间距离关系，实现了基于方向和距离关系的复合空间查询，有效地提高了空间查询的性能。

1 空间方向关系计算模型

现有的空间方向关系计算模型主要包括：锥形模型、矩形模型、方向关系矩阵模型、方向Voronoi图模型和方向关系统计模型。

矩形模型[6]用两目标的MBR之间的方向关系来确定两目标之间的方向关系，但由于MBR之间的关系在许多情况下并不能精确代表目标之间的真实关系，因此该模型是一个近似描述模型，在进行空间查询时容易出现错误的查询结果，目前已很少使用。

方向Voronoi图模型[7]借助目标间指向线法线的Voronoi 图得到目标间的方向关系；方向关系统计模型[8]通过统计目标间可视点之间的方位角，对目标间的方向关系进行描述。这两个模型的优点是对方向关系的描述较其他模型要精确，但它们的计算都过于复杂，难以满足空间查询的高效性要求。

方向关系矩阵模型[9]以参考目标的MBR为中心将空间划分为固定的八个矩形方向区域，并用源目标与各方向区域之间交的结果作为元素构成方向关系矩阵来表达空间方向。该模型的优点是计算简单、实现容易，但它只能处理八方向的空间查询，无法满足实际应用的需求。

锥形模型[10]的基本思想是：以参考目标的几何中心为起点，将空间划分为若干个锥形方向区域，并通过源目标与各方向区域之间的交来描述空间方向。图1所示为八方向锥形模型，图中源目标B相对于参考目标A的方向关系为东（E）。

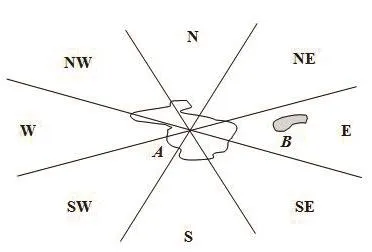
图1 锥形模型Fig.1 Conical model

由于锥形模型是针对目标本身来计算方向关系的，因此在准确性上要优于矩形模型；此外，锥形模型结构简单，在计算效率上要高于方向Voronoi图模型和方向关系统计模型，并且能够根据实际应用的不同需求，将空间划分为四方向、八方向、十六方向等锥形区域。为此，本文采用锥形模型实现基于方向关系的空间查询。

2 四叉树索引

在利用锥形模型进行基于方向关系的空间查询时，需要依次判断各空间对象与给定锥形方向区域之间的拓扑关系。因此，当空间对象的数据量不断增加时，其查询效率将会迅速下降，而解决该问题的关键是为空间查询建立合适的空间索引[11]。

空间索引是介于空间操作和空间对象之间的一种辅助性数据结构，通过它的筛选，大量与特定操作无关的空间对象被排除，使空间操作能够快速地访问操作对象，从而极大地提高空间查询的效率。目前常用的空间索引主要有二叉树索引、格网索引、R树索引和四叉树索引等[12]。

与其他空间索引相比，四叉树索引的优点是结构简单、数据冗余低，常用于加速空间对象间拓扑关系的计算。其基本思想是：将已知范围的空间划分成4个相等的子空间，如果需要可以将每个或其中几个子空间继续划分下去（树的深度由用户指定），这样就形成了一个基于四叉树的空间划分[13]。其具体构建过程描述如下：

步骤1：构建空间四叉树

首先，计算空间对象的分布范围从而确定树的根节点矩形；然后，从根节点开始，将节点矩形平均划分为4个小矩形，创建出4个子节点，并对这4个子节点递归执行此过程，直至树的深度达到给定的值。此时所构建的四叉树是一个空的满四叉树。

步骤2：插入空间对象

从根节点开始，如果当前节点包含空间对象的MBR，分2种情况插入该对象：

1）当前节点为叶节点：将空间对象插入到当前节点中；

2）当前节点为根节点或中间节点：判断当前节点的子节点是否包含空间对象的MBR，如果包含，则把该子节点作为当前节点，递归执行过程1）、2）；如果都不包含（相交或相离），则将空间对象插入到当前节点中。

步骤3：删除空节点

由上述过程创建的四叉树可能存在空节点，为节省存储空间，需要对它们进行删除。即从根节点开始，逐节点进行查找，如果当前节点没有子节点并且不含有空间对象，则删除该节点；如果当前节点包含子节点，则把子节点作为当前节点递归执行此过程，直至索引树中的所有节点都遍历完毕。

如图2所示，由于四叉树索引的根节点和中间节点都能够存储空间对象，且各节点所存储的空间对象不重复，因此有效地降低了数据的冗余，具有较好的空间索引性能。故本文选用四叉树作为空间查询的索引结构。

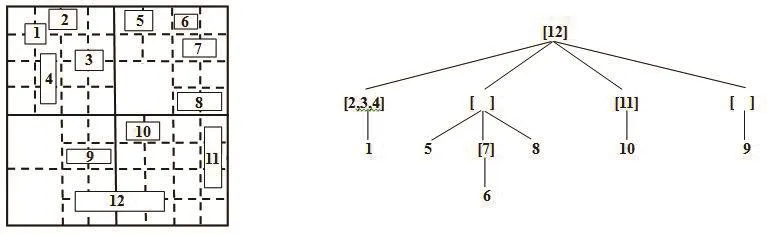
图2 四叉树索引Fig.2 Quad-tree index

3 基于方向关系的空间查询算法

在四叉树索引中，空间对象是用其MBR来表示，但是在进行基于方向关系的空间查询时，空间对象的MBR与方向区域之间的拓扑关系在许多情况下并不能正确代表空间对象自身与方向区域之间的拓扑关系。如图3所示，虽然空间对象P的MBR与给定的锥形方向区域Di相交，但P自身和Di并不相交。因此，本文将空间查询分为以下2个过程。

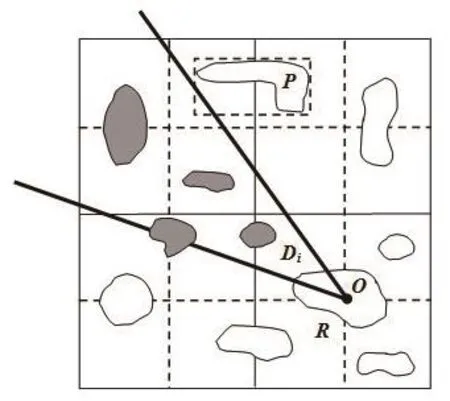
图3 基于方向关系的空间查询Fig.3 Spatial query based on direction relations

1）过滤：借助锥形模型和四叉树索引快速查找其MBR符合给定方向关系的空间对象，构成候选集S1；

2）提炼：从候选集S1中删除不符合给定方向关系的空间对象，得到结果集S2。

下面结合图3详细介绍算法的具体步骤。

步骤1：计算各空间对象的MBR，并建立它们的四叉树空间索引，详细算法参见文献[11]；

步骤2：以参考目标R的几何中心O为起点，构建给定的锥形方向区域Di，并将四叉树的根节点作为当前节点N；

步骤3：判断当前节点N与锥形方向区域Di的拓扑关系：

①当前节点N与锥形方向区域Di相离：直接返回上一层；

②当前节点N包含在锥形方向区域Di内：将节点N（包括其子节点）存储的所有空间对象加入候选集S1，返回上一层；

③当前节点N与锥形方向区域Di相交：如果节点N存储了空间对象，判断节点N中每个空间对象的MBR与Di的拓扑关系，如果相交或被Di包含，则将该空间对象加入候选集S1；如果节点N还包含有子节点，则依次把每个子节点作为当前节点N，递归执行步骤3，否则，返回上一层。

步骤4：从候选集S1中找出其MBR与锥形方向区域Di相交的所有空间对象，并判断其中的每个空间对象与Di的拓扑关系，若与Di相交或被Di包含，则保留该空间对象；否则，删除该空间对象。从而得到结果集S2，如图3中的阴影多边形。

4 基于方向和距离关系的复合空间查询算法

在实际应用中，往往需要将方向和距离关系相结合，才能对空间目标进行准确、快速地查询。如在查询图4中“位于居民地A的北面并且距离小于50 m”的地块B1时，若基于方向关系查询，则结果为B1、B4两个地块；若基于距离关系查询，则结果为B1、B2、B3三个地块。显然，在该情形下，只有将方向和距离关系相结合，地块B1才会被准确、高效地查询出来。不失一般性，下面以“在某方向并且小于指定距离”为查询条件对算法进行说明。

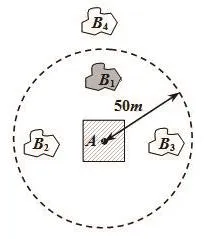
图4 结合方向和距离关系的空间查询Fig.4 Spatial query by combined with direction and distance relations

如图5所示，A表示参考对象，锥形区域表示给定的方向区域，圆形区域表示给定的距离范围。算法的基本思路是：首先，计算给定的方向区域和距离范围之间的交，如图5中的扇形区域OL1L2；然后，借助四叉树索引查找被OL1L2包含或与OL1L2相交的空间对象，得到查询结果，如图5中的阴影多边形。

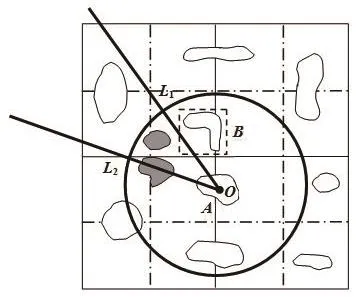
图5 基于方向和距离关系的复合空间查询Fig.5 Compound spatial query based on direction and distance relations

下面结合图5对算法的执行过程进行详细的描述。

步骤1：计算空间对象的MBR，建立四叉树索引；

步骤2：计算给定的方向区域和距离范围之间的交OL1L2；

步骤3：从四叉树的根节点开始，判断当前节点与扇形区域OL1L2之间的拓扑关系：

1）当前节点与OL1L2相离：直接返回上一层；

2）当前节点包含在OL1L2内：将该节点（包括其子节点）存储的所有空间对象加入候选集，返回上一层；

3）当前节点与OL1L2相交：如果该节点存储了空间对象，判断每个空间对象的MBR与OL1L2的拓扑关系，如果相交或被OL1L2包含，则将该空间对象加入候选集；如果该节点还包含有子节点，则把子节点作为当前节点递归执行步骤3，否则，返回上一层。

步骤4：计算候选集中其MBR与OL1L2相交的空间对象和OL1L2之间的拓扑关系：

1）空间对象与OL1L2相离：删除该对象；

2）空间对象被OL1L2包含或与OL1L2相交：保留该对象。

5 实验与讨论

为检验上述算法的查询性能，本文利用C#语言对算法进行了编程实现，并使用不同几何类型的空间对象（点、线、面）进行了实验。图6、图7是其中具有代表性的两组实验结果，在图7中，d表示地图距离单位。

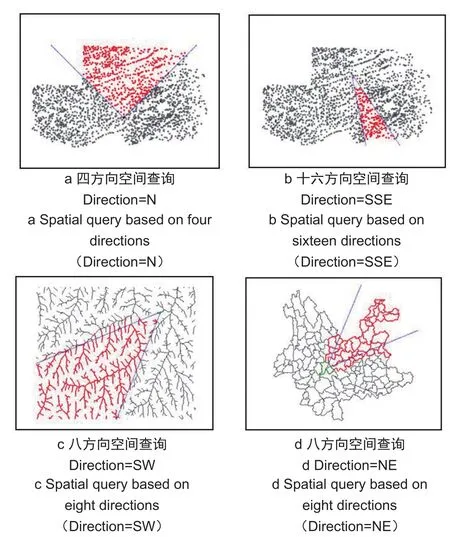
图6 基于方向关系的空间查询实验Fig.6 Experiments of spatial query based on direction relations

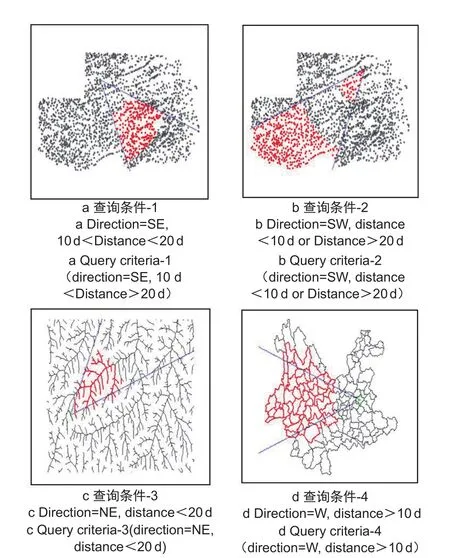
图7 基于方向和距离关系的复合空间查询实验Fig.7 Experiments of compound spatial query based on direction and distance relations

为检验算法的查询性能，本文对利用四叉树索引（树的深度为4）和不利用四叉树索引的两种复合空间查询进行了对比测试。实验环境为Intel Core2处理器（主频为2GHz），内存为2GB，测试数据采用比例尺为1:4000000的矢量线目标数据（线目标的个数为11 333）。查询条件为“Direction={N,NE,E,SE,S,SW,W,NW}and Distance＜20 d”。表1给出了两种方法查询目标对象时所需的比较次数以及执行时间，列（%）分别表示利用四叉树索引的比较次数、执行时间相对于不利用四叉树索引的比较次数、执行时间的百分比。

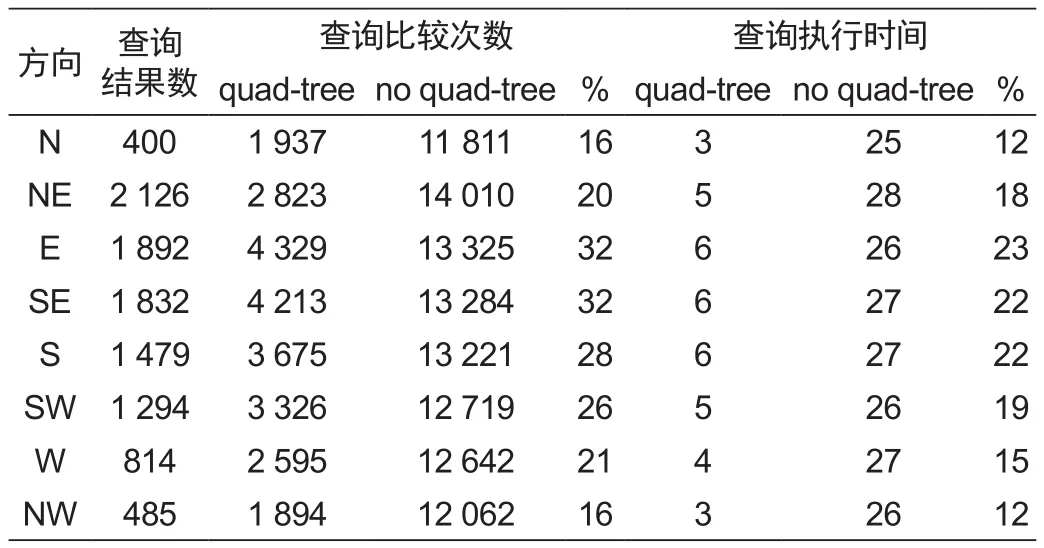
表1 查询性能对比Tab.1 Comparisons of spatial query performance

分析上述实验结果，可得出以下结论：

1）算法能够实现基于四方向、八方向和十六方向的空间查询，较好地满足了实际应用的需求；

2）算法将方向和距离关系相结合进行空间查询，有效地提高了空间查询的准确性；

3）算法能够处理不同几何类型的空间数据（点、线、面），具有较好的通用性；

4）算法采用四叉树作为空间索引结构，显著地提高了空间查询的效率；

5）算法的局限性在于，当两目标之间的距离相对于自身大小很近时，容易出现查询上的偏差。如图8所示，在利用锥形模型查询参考目标A以东（E）的空间对象时，与A邻近的目标B被漏查。

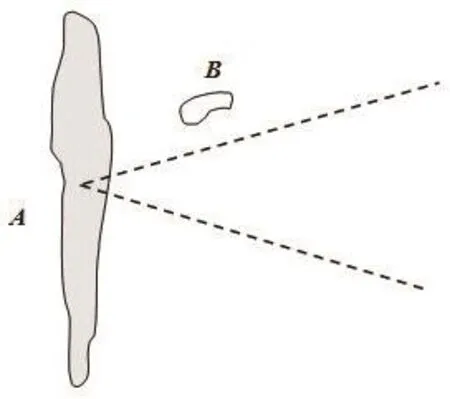
图8 锥形模型存在的缺陷Fig.8 Defects of conical model

6 结束语

本文针对方向关系在空间查询中的应用进行了研究，在分析比较现有空间方向关系计算模型及空间索引结构的基础上，选用锥形模型和四叉树索引提出了一种基于方向关系的空间查询算法，进而通过计算给定方向区域和距离范围之间的交，实现了基于方向和距离关系的复合空间查询。实验表明，提出的算法能够对不同几何类型的空间数据进行准确、高效的查询，较好地满足了实际应用的需求。但由于锥形模型自身存在的不足，导致查询结果在某些情况下出现偏差，该问题的解决有赖于空间方向关系计算模型的进一步改进与完善。