教学,应给学生留下无限可能
陈雨华


中图分类号:G632.4 文献标识码:A 文章编号:1672-1578(2018)01-0023-01
最近,听了一节北师大版三下的“分一分(一个物体或图形作为整体的分认识)”。课堂目标定位精准,构思巧妙,板块设计合理,课堂气氛也调节的比较活跃,学生积极参与其中。再加上执教者对媒体使用比较熟练,使得学生对抽象的分数得以形象化的理解,为本课添了不少的色彩。
但课堂中的几个小环节却似乎不是那么的和谐。
在学生初步认识了分数之后,教师为了强调“平均分”,设计了这么一道习题:图一中哪几幅图是不能用几分之几表示的?为什么?
设计者的本意可能是想告诉学生,只有常规图形才能得到“平均分”(估计执教者仅仅局限于动手“折”图形了),而只有“平均分”了才能得到分数。于是课堂上在师生的“努力”下得出结论只有梯形不能平均分。实际上,稍微有点几何常识的人都知道,梯形无论想分成多少等份,都是容易实现的。甚至扩展到其它一般图形我们也总是有办法“平均分”的。退一步说,教材上连不可能那么规则的“苹果”都能一分为二得到二分之一了,更何况图形呢?
在巩固练习环节,教师又设计了这样一道判断题,图二中涂色部分是整个图形的1/3。()
学生又很自然地在老师引导下打出了一个大大的叉。然而,我们都知道只要通过简单的证明,就能得出图中的阴影部分的的确确正好占整幅图的1/3。有心的老师会发现这幅图非常熟悉,因为教材上就有,只不过教材上是呈现的是下图三。而图三的阴影当然不能用1/3来表示了。
以上两个例子显然是因为教师只停留于表面去思考问题,犯下了低级的错误。或许,有教師会认为,限于三年级的学生的知识储备,这样的结论对学生是没有任何影响的。建构主义观点认为,在学生学习的过程中,受学生心理能力、知识条件等的影响,我们允许学生在知识的建构过程中出现暂时的或者说阶段性的错误。例如,二年级学生认识的平行四边形就都是“倾斜的”,在他们的头脑中长方形和正方形都不是平行四边形。三年级学生认为梯形不能“平均分”,认为图二没有“平均分”,就不能用1/3来表示阴影等,这些都是学生知识建构过程中的暂时性、阶段性的错误,都是可以包容的。
从学生知识掌握的角度分析,对于这样的观点,笔者也是认同的。就本课而言,面对只有小学三年级的学习对象,去探讨如何给梯形等分,图二的阴影是否为1/3等知识显然是没有必要的。但是从培养学生的创新能力,或者说培养学生的猜想能力、想象能力还有直觉能力等角度出发,我们是否在人为的设置了一道枷锁呢?因为,这里的教学路径,它是指向封闭的,而非开放的;指向单一的,而非多元的。很多时候,学生虽然说不出为什么,虽然可能想像不出怎么去给梯形“平均分”,虽然证明不出图二的阴影正好是1/3,但至少有部分学生是有这方面的猜测的,或者说是有这种直觉的。而现在老师简单的告诉他,这样是不可以的,创新的苗头显然都给掐灭了。
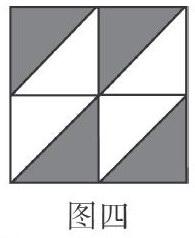
实际上,也正是因为课堂中的这种限制,导致课堂最后在判断图四的阴影能否用1/2来表示时,学生异口同声地认为不能,且无论教师如何开导,都无效,因为现在的学生的思维被僵化了,他们已经很难去“变通”了。
为什么课堂中,我们总是告诉学生不能这样,不能那样,这样不对,那样不行呢?而不是告诉学生,除了这样,还可以那样,甚至还可以怎么样。我们的教学应留给学生无限的可能,而不是去限制学生的猜想与想像。我们应给学生足够质疑与提问的空间,给学生足够探索与实践的空间、给学生足够评价与反思的空间。更重要的是,我们要变“封闭的问题”为“开放的问题”、变“单一路径”为“多向路径”,变“不能”为“可能”,为学生留下无限的发展空间,成就他们明日的精彩。

