基于PWM技术的平移式变量喷灌机喷头流量分配方法
莫锦秋 周志宇 陶 帅 李彦明
(上海交通大学机械与动力工程学院, 上海 200240)
0 引言
随着水资源的日益短缺,推广高效节水灌溉技术势在必行。在变量灌溉技术中,根据土壤墒情、作物长势、作物生长需求等参数,依据灌溉决策模型决定各土地决策单元的需水量,形成处方值,由喷灌机按处方值进行喷灌作业。
变量灌溉技术在大型喷灌场合具有广阔应用前景。大型平移式喷灌机通常由几跨装有喷头的桁架相连而成,桁架由若干个行走塔架支承并完成移动,桁架方向与机组移动方向垂直。目前比较常用的变量灌溉方法是通过调节行走速度来改变灌溉量。而脉冲宽度调制(Pulse width modulation, PWM)变量灌溉则是在各个喷头之前安装开关电磁阀,通过调节PWM信号的占空比来控制喷水与停喷的时间比,从而改变喷头流量,相对于调节行走速度,该方法能够实现更精准的变量灌溉[1-2]。
各类平移式喷灌机,包括Valley、Lindsay等大型产品,各个喷头喷洒区域都有较大部分的重叠。目前对于喷灌机喷洒特性的研究,大多数着重于喷头组合水量分布研究,少见进行喷头流量分配,尤其是沿桁架方向处方值变化时喷头流量分配的相关研究。如严海军[3]通过编写软件,模拟了圆形喷灌机及平移式喷灌机桁架方向喷洒均匀度与喷头间距的关系,并据此提出了喷头间距优化策略。HANKS等[4]经实验得出喷头间距为湿润直径的20%~25%时喷洒均匀性最好的结论。O’SHAUGHNESSY等[5]在实验过程中发现,相邻管理区的处方值不同时,对喷洒效果将会产生严重影响,提出了在不同处方的灌溉区间设立过渡区的解决方法。此外,喷头水量分布规律及喷灌机速度、工作压力、喷头组合形式等因素对水量分布及均匀性的影响也是主要研究方向[6-13]。
本文对平移式喷灌机进行PWM变量灌溉时如何将处方值转换为各喷头的分配流量展开研究,给出喷头流量分配的加权均分法和遗传算法分配法(Genetic algorithm, GA),通过分析两种方法在处理处方值突变和喷洒均匀性上的特性,进一步将两种方法进行组合,以保证相邻处方值突变时的高喷洒精度和均匀变化处方值时的高喷洒均匀性。
1 喷头流量分配问题定义
1.1 重叠喷洒与喷洒管理区
PWM变量喷灌在总水管供水泵变频恒压控制的基础上进行喷头出水占空比控制、在不改变喷洒水压情形下改变流量。由于水压不变,在喷嘴型号、喷头离地高度确定时单喷头瞬间喷洒空间分布特性可视为不变。图1是陈震等[14]将实验测得的150 kPa水压、无风条件下Nelson R3000型喷头喷洒分布数据插值得到的单喷头喷洒特性。由图1可知,若喷头间距等于喷头喷洒直径时,喷洒均匀性较差。
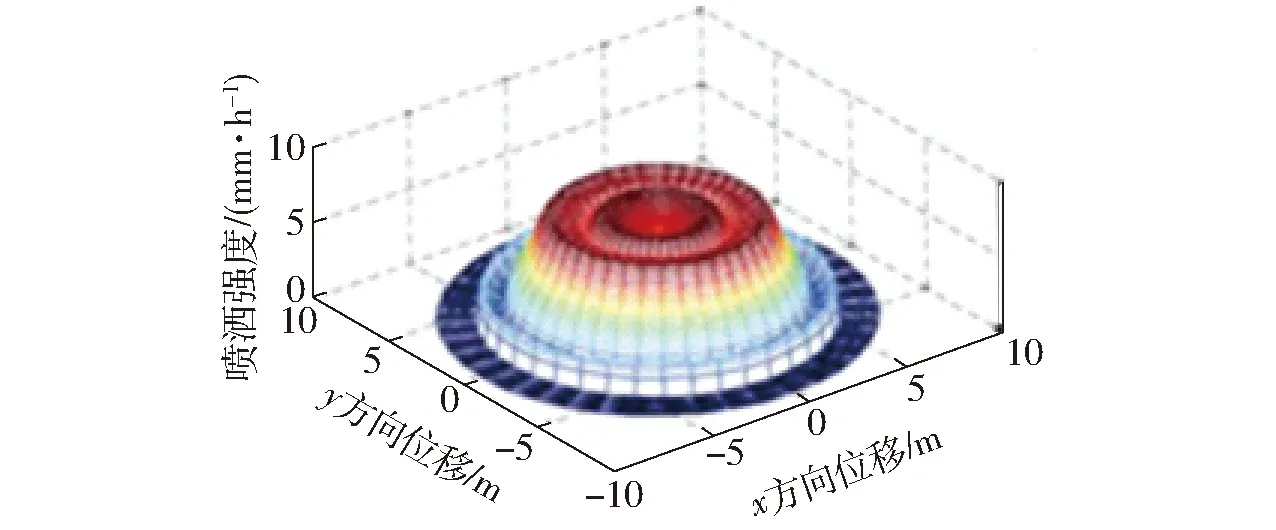
图1 Nelson R3000型喷头水量分布Fig.1 Water distribution of Nelson R3000 sprinkler
喷灌机上喷头间距不同,相邻喷头喷洒重叠情况也不同。图2为参照HANKS等[4]的实验研究结论以喷头喷洒直径的1/4设置喷头间距。将相邻喷头重叠区域定义为最小水量控制单元,即喷洒管理区。图2中相邻10个喷头喷洒重叠形成7个管理区,管理区宽度为喷洒直径的1/4,各管理区水量是相邻几个喷头重叠喷洒在此管理区内的水量之和。图2所示沿桁架方向的前端和末端各有3个管理区涉及的喷头少于4个,而桁架中间的各个管理区则均由4个喷头控制水量,为区分分别命名为不完全管理区和完全管理区。
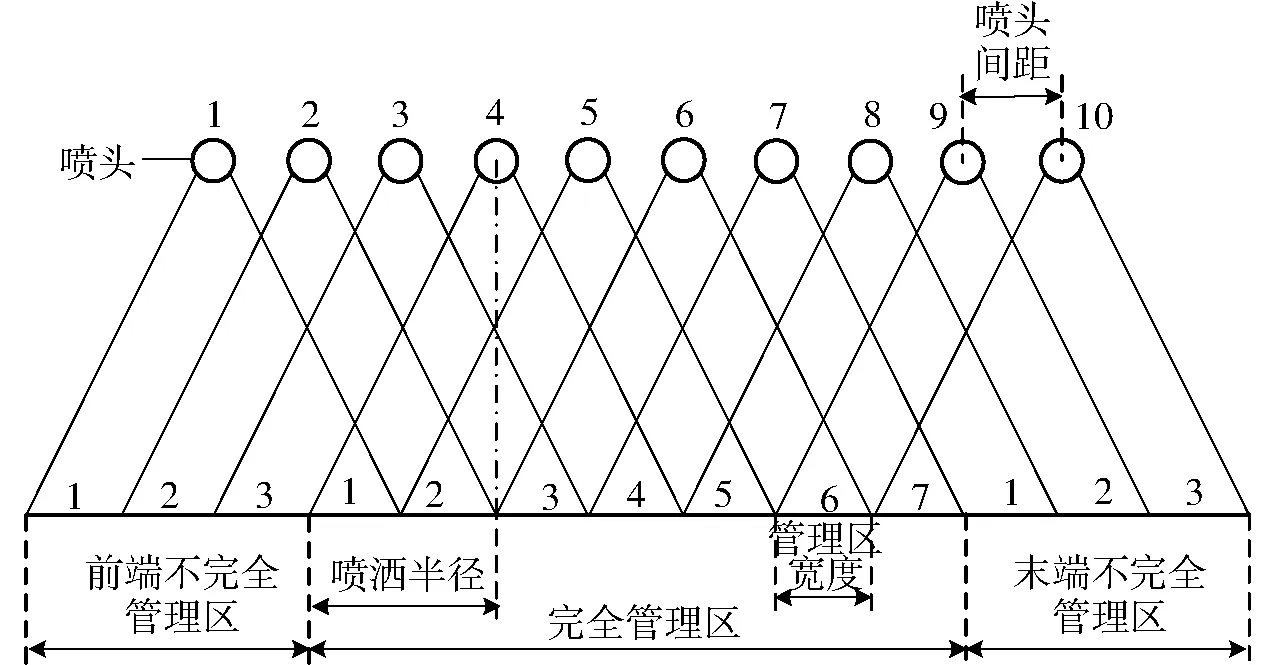
图2 相邻喷头喷洒重叠区域示意图Fig.2 Sketch of overlapped areas of adjacent sprinklers
由图2扩展可得相邻喷头数为n时,喷头间距d、喷头喷洒半径R、管理区宽度L间有
d=L=2R/n
(1)
由N个喷头构成的喷灌机若按n个相邻喷头重叠喷洒则存在M个完全管理区,即
M=N-n+1
(2)
同时在桁架前、末端分别存在n-1个不完全管理区。
1.2 重叠喷洒喷头数的确定
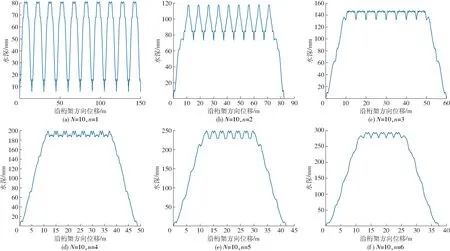
图3 沿桁架方向的叠加水量分布Fig.3 Overlapped water distribution in lateral direction
图3为采用陈震等[14]的单喷头喷洒分布实验数据,各喷头取陈震等[14]实验时的相同水量,取N=10,n=1,2,…,6时的沿桁架方向剖面的水量叠加分布。从图3知,当多个喷头喷洒重叠后,各完全管理区相对波动明显减小。
图3仅为沿桁架方向单维度的水量波动。图4中按桁架方向和前进方向将作业地块离散成Mg×Ng个小区块构成二维地块坐标系(mg,ng),同理每个喷头的喷洒范围也同样可离散成Ms×Ns个小区块,构成喷头局部坐标系(ms,ns)。
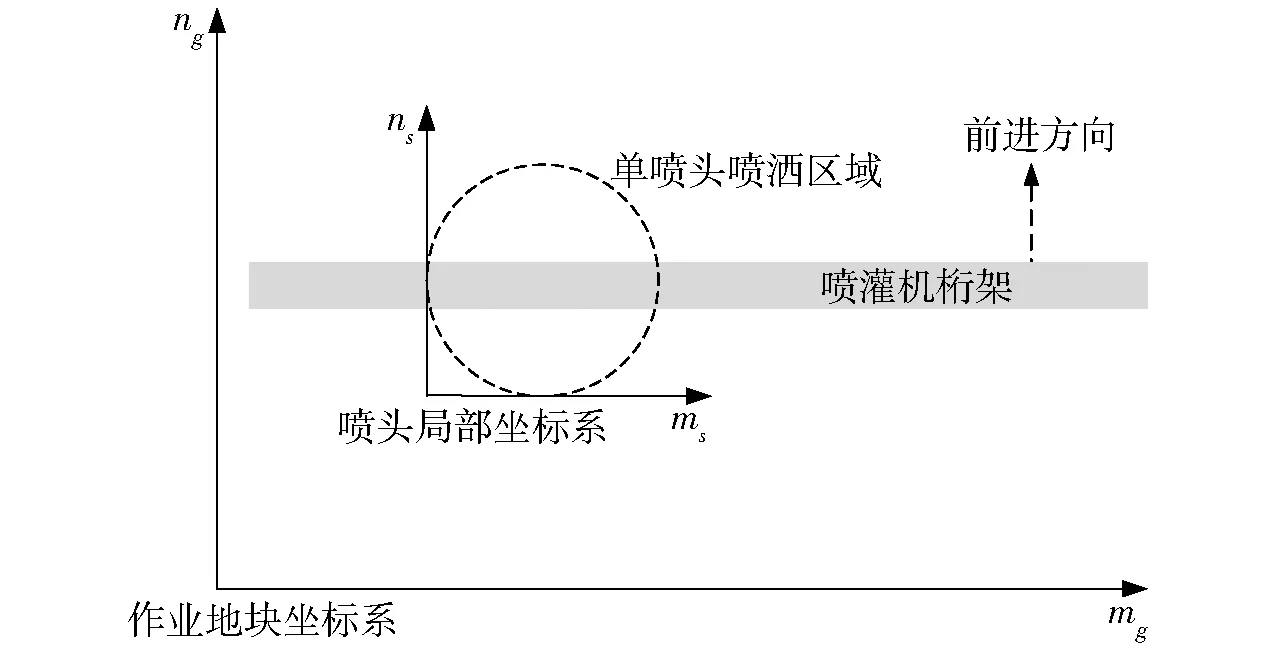
图4 区块离散示意图Fig.4 Sketch of discrete areas
定义喷头的喷洒分配率λs(ms,ns)为单个喷头局部坐标某个小区块(ms,ns)内的流量占此喷头总流量的百分比,喷头喷洒时将喷头流量q(t)分配喷洒到各个局部(ms,ns)区块内
qs(ms,ns,t)=λs(ms,ns)q(t)
(3)
其中
(4)
(5)
式中其他情形指不在此喷头喷洒范围内的情形。
喷灌机作业时作业地块上某个小区块(mg,ng)的当前流量qg(mg,ng,t)为喷灌机所有喷头在当前区块上的流量总和,即
(6)
式中qk(t)——第k个喷头的当前流量
λg(mg,ng,k,t)为小区块(mg,ng)映射到第k个喷头当前的局部区块(ms,ns)对应的流量分配率。其中ms与第k个喷头在桁架位置有关,ns与第k个喷头当前前进方向的位移有关,匀速前行时则与时间直接线性相关。由式(4)知当喷头布置或行走使得第k个喷头的当前喷洒区域不在小区块(mg,ng)时λg(mg,ng,k,t)=0。
喷灌完成后,区块(mg,ng)内喷灌水量Vg(mg,ng)为
(7)
取N=10,n=1,2,…,6,喷灌机匀速前进时,按上述算法,采用陈震等[14]的单喷头数据,应用Matlab编程得出二维水量等高线图,如图5所示。

图5 二维叠加水量分布等高线图Fig.5 Two-dimensional contour plots of overlapped water distribution
表1是对应于图5的沿桁架方向各完全管理区的喷洒均匀系数Cu和Du,其中克里斯琴森均匀系数Cu和分布均匀系数Du分别定义[15-18]为
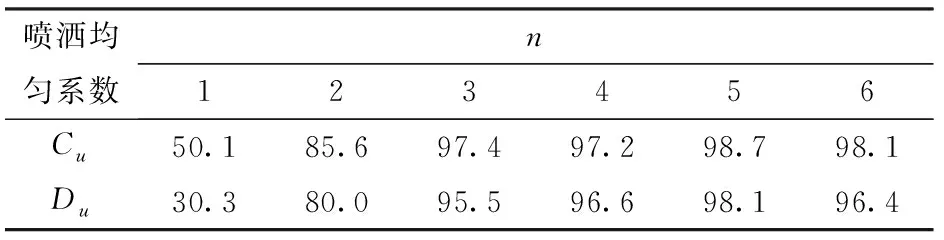
表1 沿桁架方向各完全管理区的喷洒均匀系数Tab.1 Coefficient of uniformity of complete management zone in lateral direction %
(8)
(9)
式中I——计算网格数
hi——第i个计算点的喷灌水深,mm


相比而言Du可防止个别测量点出现喷洒异常甚至漏喷所导致的喷洒水深与均值相差过大。
由图5和表1知,多喷头组合喷洒时喷洒均匀性普遍优于单喷头喷洒,重叠喷头数达到4和5时Cu和Du都能达到较高值,这与HANKS等[4]实地实验结论相一致。从设备角度出发,叠加喷洒喷头数越多,喷头控制越复杂、制造维护成本越高,结合表1取n=4,即一个管理区由相邻4个喷头重叠喷洒控制是一个保证喷洒均匀性和经济性的选择。
1.3 喷头管理区喷洒分配率
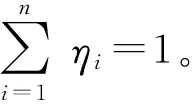
当喷灌机组匀速前进时,单喷头定流量喷洒扫掠完成后,沿桁架方向将形成一个单维的水量分配率λss(ms),即单喷头沿桁架方向的水量Vss(ms)与当前喷头的流量q间有
Vss(ms)=qΔtλss(ms)
(10)
n个喷头重叠喷洒布置时,单喷头流量分配到n个管理区,沿桁架方向分别对各个管理区内的λss(ms)求和,得到喷头区域喷洒量分配率ηi,即落入单个管理区内的流量占单喷头总流量的百分比。
采用陈震等[14]的喷头实验数据,并设喷灌机匀速前进,喷头喷洒扫掠可求得4喷头重叠喷洒布置时有η1=η4=13.78%、η2=η3=36.22%。
按1.2节的分析结果,本文将针对相邻4个喷头控制一个管理区的情况。当喷灌机生产制造、喷头选型等因素导致控制一个管理区的喷头数发生变化时,对于不同喷头、不同工况、不同分区数量,均可以由单个喷头的喷洒特性得到喷头管理区喷洒分配率。以相邻5个喷头控制一个管理区为例,喷灌机首尾各出现4个不完全管理区。此时每个喷头涉及5个管理区,对应的喷头管理区喷洒分配率分别为η1、η2、η3、η4、η5。
1.4 喷头流量分配定义
当每个管理区流量由相邻多个喷头共同决定时,就涉及到管理区处方值到单个喷头流量的转换分配问题。本文取n=4按完全管理区处方值要求的喷头流量进行分配。如图2所示,各完全管理区由相邻4个喷头控制,且有完全管理区数M=N-3。
喷头流量分配问题可以具体化为:已知各个管理区的设计处方值时,分配各个喷头流量,使得各管理区的分配流量与处方值之间的偏差尽量小。管理区流量分配偏差指标有:
(1)管理区流量分配误差ei,即管理区分配流量qhi与处方值qpi之差除以设备最大处方值qpMAX。
(11)
(2)最大流量分配误差eME,即管理区流量分配误差绝对值的最大值
eME=max(|ei|) (i=1,2,…,M)
(12)
(3)流量分配平均绝对误差eMAE,即管理区流量分配误差绝对值的平均值
(13)
(4)流量分配均方根误差eRMSE,即管理区流量分配误差的标准差
(14)
O’SHAUGHNESSY等[5]在实验过程中发现,相邻管理区的处方值不同时,对喷洒效果将会产生严重影响。对应地本文以沿桁架方向N个喷头形成的M个完全管理区,在第Jp个管理区产生处方值阶跃进行研究。设各管理区的处方值qpi为
(15)
式中qps——流量处方值阶跃初值
qpe——流量处方值阶跃终值
并且可得流量处方值阶跃幅度
Δqp=qpe-qps
(16)
上述流量变量qpi、qps、qpe、Δqp在流量分配计算时可取与设备最大的处方值qpMAX的百分比表达。
本文后续分析中取N=20,即M=17。各流量处方值阶跃前后的取值组合如表2勾取处。对表2中每一个处方值组合,分别取Jp=2,3,…,17进行求解计算。后期为细化分析分配误差的变化情况,又增加了Δqp取15%、33%、52%的组合。
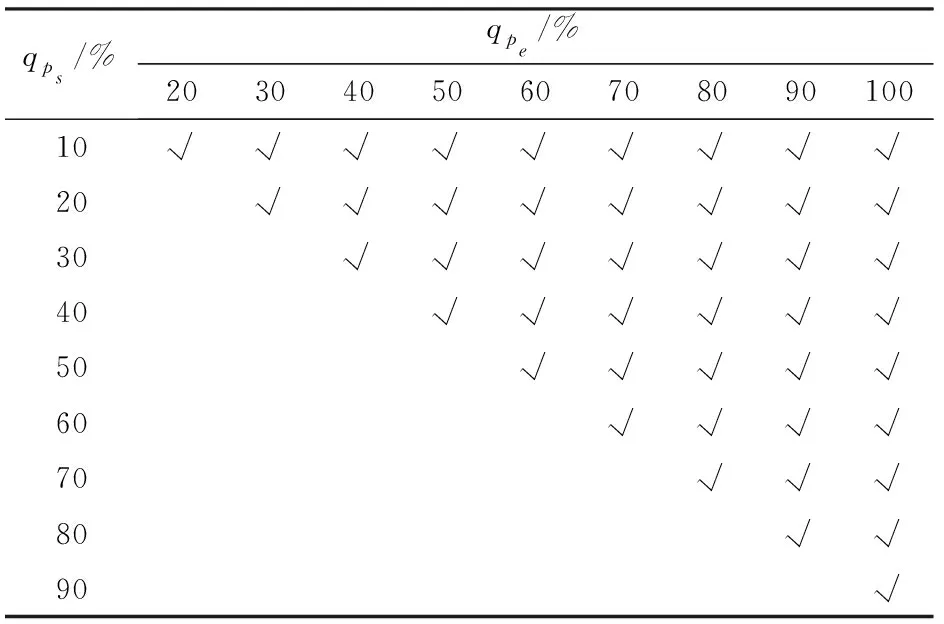
表2 处方值组合Tab.2 Combination of prescriptions
2 基于喷头区域喷洒量分配率的喷头流量分配
2.1 喷头流量的分配法
2.1.1喷头流量的平均分配法(加权均分法)
目前Lindsay等喷灌机厂商均采用流量均分法,即喷头流量为该喷头控制的管理区的处方值的平均值。按图2所示,喷头排序从桁架上首个喷头起,管理区排序从首个完全管理区开始。对应n=4,完全管理区内有
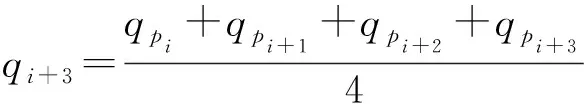
(17)
式(17)中分配给第i+3个喷头的流量qi+3是此喷头喷洒到的4个相邻管理区的处方值qpi、qpi+1、qpi+2、qpi+3的平均值。而实际上,由1.3节可知,每个喷头在4个管理区的区域喷洒量分配率并不都是1/4,而应该分别为η1、η2、η3、η4。对式(17)以区域喷洒量分配率进行加权后得到加权均分法的喷头流量分配式
qi+3=η1qpi+η2qpi+1+η3qpi+2+η4qpi+3
(i=1,2,…,N-6)
(18)
式(18)仅适用于中间的N-6个喷头,如图2中的喷头4、5、6、7。最前端和最末端的各3个喷头因为涉及非完全管理区而无法采用式(18),其流量则可通过补足所涉完全管理区处方值的方式求取。以图2中的完全管理区3为例,其实际喷洒量由q3、q4、q5、q6共同决定,而q4、q5、q6已由后续的完全管理区按式(18)确定,因此可以通过补足处方值qp3得到
(19)
同理已知q3、q4、q5后向桁架前端递推得
(20)
同理已知q2、q3、q4再后向桁架前端递推得
(21)
同理对桁架末端喷头可得
(22)
(23)
(24)
第i个完全管理区内的管理区分配流量qhi是它所涉的4个喷头喷洒在本管理区的流量总和
qhi=η4qi+η3qi+1+η2qi+2+η1qi+3
(i=1,2,…,N-3)
(25)
由式(11)可得各管理区分配流量误差ei。对于中间的M-6个完全管理区,由式(18)、(25)可得
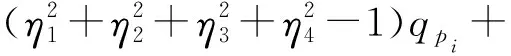
(26)
由式(26)可知,ei与当前管理区及其前后相邻3个管理区共7个管理区处方值有关,但误差不会传递到其他管理区上。误差最小值可达到0,但当相邻处方值变化较大时,误差增加可观。如当qpi-3=qpi-2=qpi-1=qpi+1=qpi+2=qpi+3=qpMAX而且qpi=0时,误差达到最大值。
2.1.2喷头流量的遗传算法分配法(GA法)
遗传算法依照生物进化,将实际问题映射为环境,将问题解转化为一系列基因编码的染色体,通过复制、组合交叉及变异产生后代种群,按照优胜劣汰、适者生存的原则筛选出适应性最优的染色体种群,亦即解集[19-21]。
喷头流量分配问题的优化设计变量为喷头流量序列
(27)
优化目标为管理区分配流量与处方值间的偏差,适应度函数可取
(28)
遗传算法中,初始值按2.1.1节的加权均分法取得,不断循环地找出某个种群中使适应度函数达到最小值的染色体,参与到下个迭代的遗传过程以产生更优良的新染色体,直至适应度达到设计要求,管理区分配流量与设计处方值之间偏差足够小。
对于非4个喷头控制一个管理区也可采用加权平均法和GA法确定喷头流量。以相邻5个喷头控制一个管理区为例,采用加权均分法时中间喷头的流量取其涉及的5个管理区的处方值的加权平均值,同时仿照式(19)~(24)通过将前端和末端的各4个完全管理区水量补足的方式取得前端和末端各4个喷头的流量,GA法则是在加权平均法的基础上进行优化。
2.2 管理区流量分配精度分析
2.2.1流量分配误差与处方阶跃初值的关系
采用表2处方值组合进行两种分配方法的流量分配,均发现流量分配误差与处方阶跃初值无关。如以Δqp=33%、Jp=9为例,采用GA法进行流量分配,当qps取不同值时,各流量分配误差如表3所示。
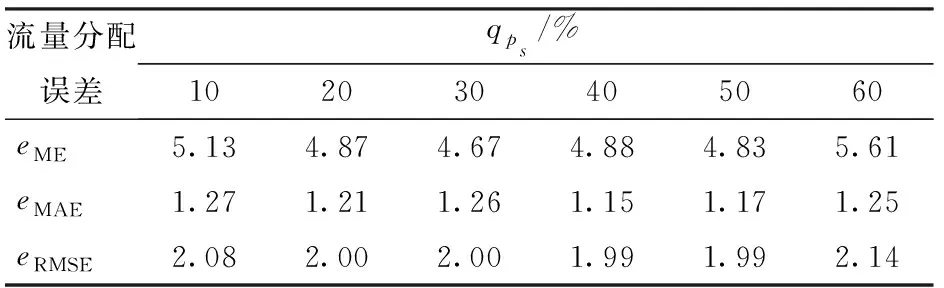
表3 不同阶跃初值下的流量分配误差Tab.3 Flux distribution error of different starting values %
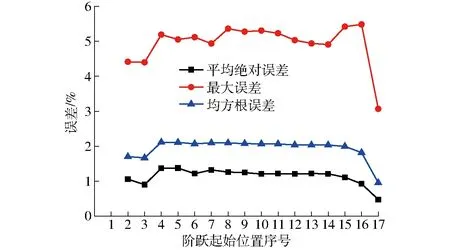
图6 不同阶跃起始位置时的流量分配误差Fig.6 Flux distribution error of different starting points
2.2.2流量分配误差与处方阶跃点的关系
采用表2处方值组合进行两种分配方法流量分配,发现当阶跃发生在两端时,误差较小;阶跃发生在中间位置时流量分配误差与处方阶跃点无关。如以qps=10%、qpe=43%为例,采用GA法进行流量分配,当Jp取不同值时,各流量分配误差如图6所示。
2.2.3流量分配误差与处方阶跃幅度的关系
图7是采用表2处方值组合进行两种分配方法的流量分配,按不同的阶跃幅度得到的管理区流量分配误差。加权均分法的各类流量分配误差会随着阶跃幅度的增大而线性增大。GA法的eME小于加权均分法,且随着阶跃幅度增大而增大。当Δqp在50%左右时,两种算法的eME差距最大,GA法优化效果最明显。当Δqp取15%、33%、52%时,eME分别约为2%、5%和10%。因此为保证较好的流量分配精度,制定处方图时相邻管理区的处方值差不宜超过最大处方值的33%。GA法的eMAE和eRMSE均小于加权均分法,而eRMSE变化趋势与eME相类似。GA法的eRMSE始终小于加权均分法,说明GA法得到的各管理区分配误差波动小。可见GA法得到的流量分配精度高于加权均分法,尤其适用于处理相邻处方值存在较大突变的情况。当相邻处方值的变化幅度在33%以内时,分配精度可以控制在5%以内。

图7 不同阶跃幅度时的流量分配误差Fig.7 Flux distribution error of different variations of prescriptions
O’SHAUGHNESSY等[5]的中心支轴喷灌机实验中,以相邻12个喷头为一个等水量灌溉区。为避免水量干扰,保证灌溉区内的均匀度及喷洒精度,三跨喷灌机在灌溉区间设置3 m过渡区,而六跨喷灌机过渡区则增大至6~9 m。O’SHAUGHNESSY等[5]的等水量灌溉区按上文定义可转换为在Jp=9处发生阶跃,阶跃附近流量分配误差较大的管理区则可作为过渡区。采用GA法时如Δqp≤33%则实现5%的管理区流量分配精度,从而无需在相邻管理区之间设置过渡区域,可大大提高土地利用率和喷灌机使用效率。
2.2.4阶跃引起的流量分配误差传递
GA法进行全局优化,相邻管理区有可能会彼此影响并导致误差向两侧传递。图8给出qps=10%、qpe=43%时在不同位置进行阶跃的管理区流量分配误差变化。从图8可以发现,阶跃处的流量分配误差将远远大于其他位置上,误差向两侧逐渐衰减。当误差向两侧各传递一个管理区后,衰减到最大误差的一半以下,因此可以认为由于处方值阶跃而产生的喷洒误差出现在阶跃处左右各两个管理区内。
3 基于管理区流量喷洒均匀性的喷头流量分配改进
图9是按O’SHAUGHNESSY等[5]的实验情况,在Jp=9处以qps=10%分别引入qpe为43%、62%和100%的处方值阶跃,采用GA法进行喷头流量分配,并采用陈震等[14]的Nelson R3000型喷头空间喷洒分布特性在喷头径向扩展,得到沿桁架的分配流量分布,其中桁架方向各处的分配流量以最大处方值的百分比形式给出。从图9可知,引入Nelson R3000型喷头喷洒分布特性后,非阶跃处喷洒均匀性差,这是GA法全局优化时,仅保证管理区分配流量精度指标,相邻喷头分配的流量差异可能较大。由式(26)知加权均分法在处方值序列均匀变化或者不变时ei可以达到0,而GA法只能做到无限趋近于0。
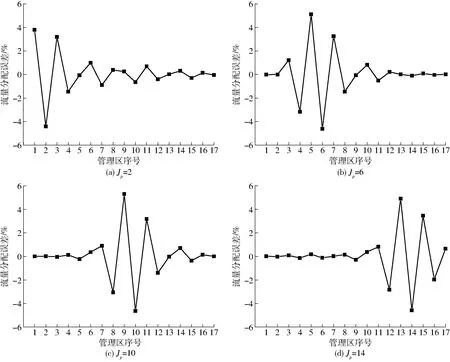
图8 GA法的分配误差传递Fig.8 Distribution error spread of GA method
将加权均分法和GA法进行组合,便形成喷头流量分配的组合法。即在处方阶跃处附近采用GA法,减少阶跃引起的管理区流量分配误差;在非阶跃处采用加权均分法,减小相邻喷头流量差,提高喷洒均匀性。由2.2.4节知GA法在阶跃左右各两个管理区内产生显著误差,因此可以只对这4个管理区及其涉及的7个喷头进行优化,然后使用加权均分法确定其他喷头的流量。对图9的场合运用组合法重新进行流量分配和喷头喷洒特性叠加,得到组合法时的分配喷洒分布,见图10。对比图9,图10中非阶跃处喷洒均匀性有明显提高,误差控制在5%内。
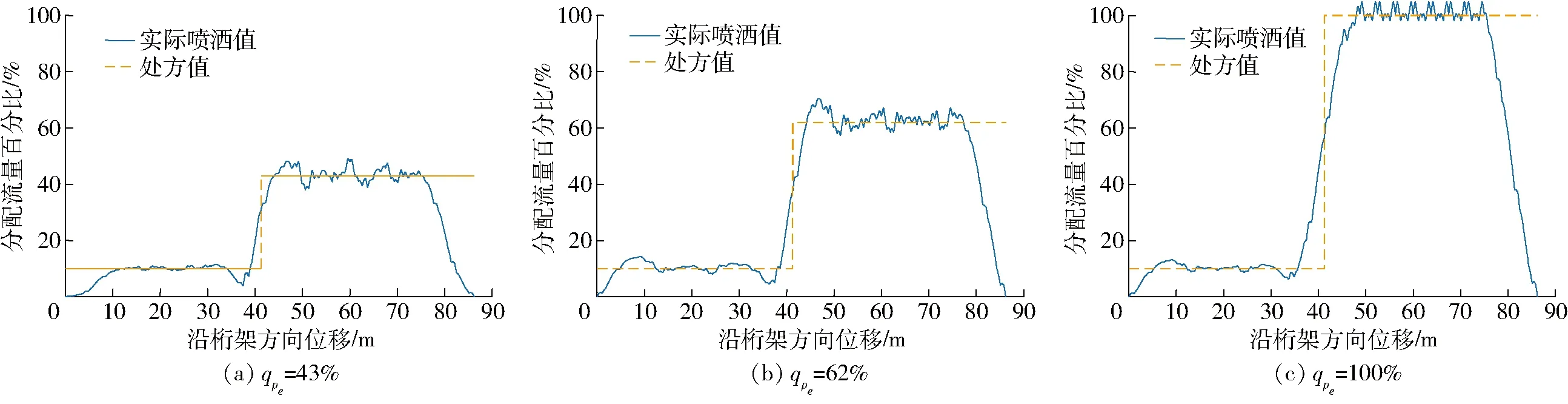
图9 采用GA法的分配流量分布Fig.9 Water distribution of GA method
图10 采用组合法的分配流量分布Fig.10 Water distribution of combined method
组合法中加权均分法的引入虽然会在一定程度上降低GA法的计算精度,但误差可以控制在较小范围内。而非阶跃部分的喷洒均匀性得到了显著的提高。
随着大型喷灌机喷头数量增多,如全局应用GA法则运算时间将急剧增大。采用组合法将缩短运算时间,降低控制器配置要求。
4 结论
(1)给出了大型平移式PWM变量喷灌机按处方值进行喷头流量分配的方法,并讨论其实现的精度和均匀性。基于Nelson R3000型单喷头水量分布实验数据,分析了多喷头喷洒叠加后的喷洒均匀性,确定了相邻4个喷头重叠喷洒控制一个管理区的喷头间距布置,并得到了喷头喷洒区域的喷头管理区喷洒分配率。
(2)结合重叠喷头的喷头管理区喷洒分配率,构建了按处方值进行喷头流量分配的加权均分法和GA法。通过对处方阶跃时的流量分配误差分析发现,采用GA法,处方阶跃幅度小于33%时,流量分配误差在5%之内;GA法最大流量分配误差出现在阶跃处,并影响附近4个管理区。
(3)通过分析叠加喷头的喷洒特性,发现全局GA法对喷洒均匀性具有不利影响。所提出的将GA法和加权均分法组合运用的组合法,综合了GA法处理相邻处方值突变时的高喷洒精度和加权均分法处理均匀变化处方值时的高喷洒均匀性。

