越冬期麦田地表蒸散量估算模型适用性分析与参数修正

程 强 徐 嫱 陈 超 孙宇瑞 王忠义 薛绪掌

(1.中国农业大学信息与电气工程学院， 北京 100083； 2.北京农业智能装备技术研究中心， 北京 100097)

0 引言

地表蒸散量是土壤水分和热量平衡的重要影响因素，也是作物需水量估算以及农田水分管理的重要依据[1-2]。冬季，温度降低，作物进入休眠期，蒸腾作用往往忽略不计，只考虑土壤表层的蒸发作用。此外，越冬期积雪覆盖和土壤中冰的形成降低了地表蒸散量，因此，在研究冬季土壤水热运移过程时，前人通常将冬季土壤的蒸发量简单地设置为零或忽略不计[3]。但研究证明，冬季蒸发确实存在，且对土壤的水热运移及分布具有重要影响[4]。因此，越冬期地表蒸散量的准确估算不仅能够为春季作物生长过程的水分管理提供重要依据，还对揭示土壤与环境之间的质量与能量交换规律有着重要意义。

蒸散量的测量可分为实际测量和理论计算两种方法。实际测量包括水量平衡法、蒸渗仪法、涡度相关法、波文比能量平衡法以及遥感法等[5]。其中，蒸渗仪法近年来在我国得到了普遍开展[6-9]，测量精度较高，但是该方法要求取样具有代表性，且需要定期校正标定系数，操作复杂。理论计算是指利用气象数据通过蒸散模型进行估算。目前，有多种模型可估算地表蒸散量，但是由于气象环境和土壤条件的多样性，很难确定唯一的适用性较广的模型[10]。FLERCHINGER等[11]在1989年提出的SHAW模型能够用于估算冬季地表蒸散量。成向荣等[12]、刘峻明等[13]用SHAW模型模拟冻融过程中土壤中水、热、蒸发量等的运移过程，并验证了其具有较高的预测精度，证明了SHAW模型在冬季土壤条件模拟的适用性。

由FAO提出的PM模型[14]以其坚实的理论基础和较高的计算精度，经常用于蒸散量的预测。但是当地表植被组成复杂或无植被时预测精度不高，且需要大量的气象数据与相关参数作为计算基础，在数据缺乏时难以准确预测[15]。文献[16-18]利用PM模型和Penman修正公式对全年的蒸散量进行估算，发现其相对误差在11—2月较大，不适用于冬季蒸散量的预测。PT模型对PM模型进行简化，不考虑空气动力学的影响，以平衡蒸发为基础，引进常数α，进行蒸散量的预测。α为经验参数，受地理特征和年降水量的影响，具有年际和季节的时间变化特性，需要对α进行调整来修正模型[15,19-20]。但是这两种模型能否用于越冬期蒸散量的预测还有待验证。为此，本文首先对SHAW、PM和PT模型在默认或经验参数下估算的冬季地表蒸散量与实际蒸散量进行比较，分析模型估算误差，在此基础上对模型参数进行修正，并借助第2年冬季的实际测量数据评价模型的适用性。

1 材料与方法

1.1 模型介绍

1.1.1PM模型

由FAO提出的Penman-Monteith (PM)模型具有坚实的理论基础和较高的计算精度，被广泛用于蒸散量的预测。在计算作物蒸散量时，由于地表及作物冠层气象环境的复杂性、作物种类、区域环境等的差异性等，FAO规定用PM模型来计算作物的参考作物蒸散量作为标准方法。该方法假设作物为0.12 m高的苜蓿，表层阻力为70 s/m，反射率为0.23，其计算公式为

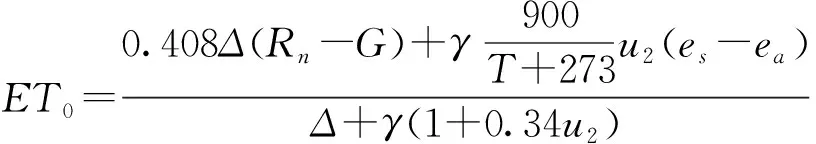
(1)

式中ET0——参考蒸散量，mm/d

Rn——作物表层净辐射，MJ/(m2·d)

G——土壤热通量，MJ/(m2·d)

T——2 m高处的日平均温度，℃

u2——2 m高处的风速，m/s

es——饱和水汽压，kPa

ea——实际水汽压，kPa

Δ——饱和水汽压-气温关系斜率，kPa/℃

γ——干湿计常数，kPa/℃

该模型综合考虑了空气动力学和辐射对于蒸散量的影响，其中，空气动力学项依赖于饱和水汽压亏缺(es-ea)，可由空气相对湿度得到；辐射项可由太阳辐射计算得到。

当土壤中水分充足时，实际蒸散量除与气象因素有关外，只和作物本身特性相关。因此，引入作物系数(Kc)来表示作物种类的不同对于蒸散量的影响[21]，即

ET=KcET0

(2)

式中ET——实际蒸散量，mm/d

本文中越冬期冬小麦的作物系数取0.614[21]。该系数较生长期偏低，这是因为在越冬期由于温度过低使冬小麦停止生长，主要反映的是地表蒸发量。

在未冻土中，当土壤中含水率较高时，具有较高的势能，使得水分能够相对自由地移动并容易被作物根系吸收；而含水率低时，由于毛细管力和土壤基质势的吸力，使得势能降低，水分不易被作物吸收。当势能降低到某一阈值时(通常取-1 500 kPa)，作物即受到水分胁迫[14,22]。而在越冬期的冻土中，冰的存在降低了土壤的基质势，在负温条件下，温度每降低1℃，土壤基质势降低约1 110 kPa[23]，因此冻土的土壤状态类似于水分胁迫。在水分胁迫条件下，实际蒸散量除受到气象因素和作物本身特性的影响之外，还受到土壤含水率的限制[24]。考虑到土壤冻结与未冻土壤脱湿过程的相似性，引入水分胁迫系数(KS)对PM模型进行参数修正，即

ET=KSKcET0

(3)

式中KS≤1，当KS=1时，表示无水分胁迫影响。KS值与土壤含水率(θ，m3/m3)密切相关，许多学者对两者之间的函数关系进行研究，发现在未冻土中，KS与θ之间的函数关系可用线性、幂函数以及分段函数等进行表示，两者之间的复杂关系还体现在易受气象条件、土壤类型、作物种类等的影响[24]。本文假设冻土中的KS与θ之间存在线性关系。

1.1.2PT模型

PRIESTLEY和TAYLOR于1972年提出估算蒸散量的模型

(4)

式中ETP-T——PT模型参考作物蒸散量，mm/d

α——Priestley-Taylor系数，经验值为1.26

该模型忽略了空气动力学项对于蒸散量的影响，假定ETP-T只依赖于太阳辐射和温度。α为经验参数，受地理特征和年降水量的影响，且具有年际和季节的时间变化特性，因此，需要对α进行调整来修正模型[15]。同样，在计算越冬期地表蒸散量时，由于在冻结土壤中，温度与液态水含量关系密切(土壤冻结特征曲线)[25]，本文在α基础上引入水分胁迫系数，即

ET=KSETP-T

(5)

同样假设冻土中的KS与θ之间存在线性关系。

1.1.3SHAW模型

FLERCHINGER和SAXTON在1989建立的SHAW模型主要用于植物冠层-雪-枯落物-土壤的冻融过程中的水热耦合运移，不仅可以模拟土壤的水分、温度、冻结深度、冰含量等，还可以模拟蒸发、蒸腾、能量通量等[11]。1991年加入了植物层系统，在原土壤元素的基础上，不仅可以计算土壤数据，还可以设置不同的作物种类同时存在于系统中，实现作物层内的蒸散发及能量平衡的模拟[26]。在该模型中，地表蒸发和热通量通过土壤表层的能量平衡计算获取。

模型中植物冠层蒸汽通量的变化为

(6)

其中

(7)

式中ke——冠层内的传输系数，m2/s

ρv——蒸汽密度，kg/m3

z——冠层高度，m

El——冠层的蒸发或蒸腾量，kg/(s·m3)

ρvs——饱和蒸汽密度，kg/m3

hr——相对湿度，%

Mw——水的分子质量，0.018 kg/mol

g——重力加速度，9.81 m/s2

R——通用气体常数，8.31 J/(mol·K)

TK——开氏温度，K

ψ——土壤基质势，m

θl——液态水含量，m3/m3

ac、bc——经验系数，分别取-53.72和1.32

式(6)中各项依次代表冠层内蒸汽变化量，进入冠层的蒸汽量，冠层的蒸发或蒸腾量。

枯落物层的蒸汽通量变化过程为

(8)

式中kv——枯落物层内的传输系数，m2/s

rh——枯落物层与空气之间的传输阻力，s/m

式(8)中的各项分别代表枯落物层的蒸汽变化量，进入枯落物层的净水汽通量和枯落物层的蒸发速率。

土壤中的水量通量传输过程为

(9)

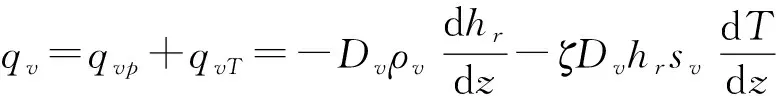
(10)

(11)

式中K——非饱和导水率，m/s

qv——蒸汽通量，m/d，由水势梯度(qvp)和温度梯度(qvT)所引起的蒸汽变化总量

θi——含冰量，m3/m3

ρi——冰的密度，kg/m3

ρl——水的密度，kg/m3

U——由于作物根系吸水所引起的源汇项，kg/(s·m3)

Dv——土壤中的蒸汽扩散率，m2/s

ζ——增量因子

sv——饱和水汽压曲线的斜率，kg/(m3·℃)

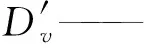
θa——土壤中空气含量，m3/m3

bv、cv——计算土壤孔隙弯曲度的系数，分别取0.66和1.0

式(9)中的各项分别代表：液态水含量的变化量，冰的变化量，进入土壤层的液态水通量和蒸汽通量，以及由作物根系吸水所引起的源汇项。

1.2 误差分析

(1)均方根误差(Root mean square error, RMSE)用于反映蒸散量估算值和实测值之间的总体差异，对特大或特小误差反映敏感。当RMSE越接近于0时，表明估算误差越小，模拟精度越高。其计算式为

(12)

式中Mi——实测值Si——模拟值

N——实测样本数

(2)平均偏差(Mean bias error, MBE)用于反映蒸散量估算值和实测值之间的平均偏差，正值表示蒸散量被高估，负值表示被低估。MBE越接近于0时，精度越高。其计算式为

(13)

(3)模型效率(Model efficiency, ME)用于表示模型的整体模拟效果，与回归方程中的决定系数(R2)类似，不同的是取值范围为(-∞～1)，当ME越接近1时，代表模型的模拟效果越好[27]。其计算式为

(14)

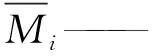
1.3 试验区概况

试验数据来源于2011—2012年和2012—2013年冬季北京市小汤山精准农业示范基地的称重式蒸渗仪系统。试验区地理位置为116°26′39″E，40°10′43″N，属于大陆性季风气候，2年的平均降水量为421 mm左右，2011—2012年冬季最高温度为3.68℃，最低温度为-9.78℃，平均温度-3.79℃；2012—2013年冬季最高温度为0.44℃，最低温度为-13.69℃，平均温度-5.24℃。2年冬季的温度和降水量数据如图1所示(“土壤冻结期”指在该时间范围内空气温度低于0℃，土壤出现冻结，下同)。可见在试验区内，土壤进入冻结期后，干旱少雨。试验区土壤质地组成等相关参数见表1。

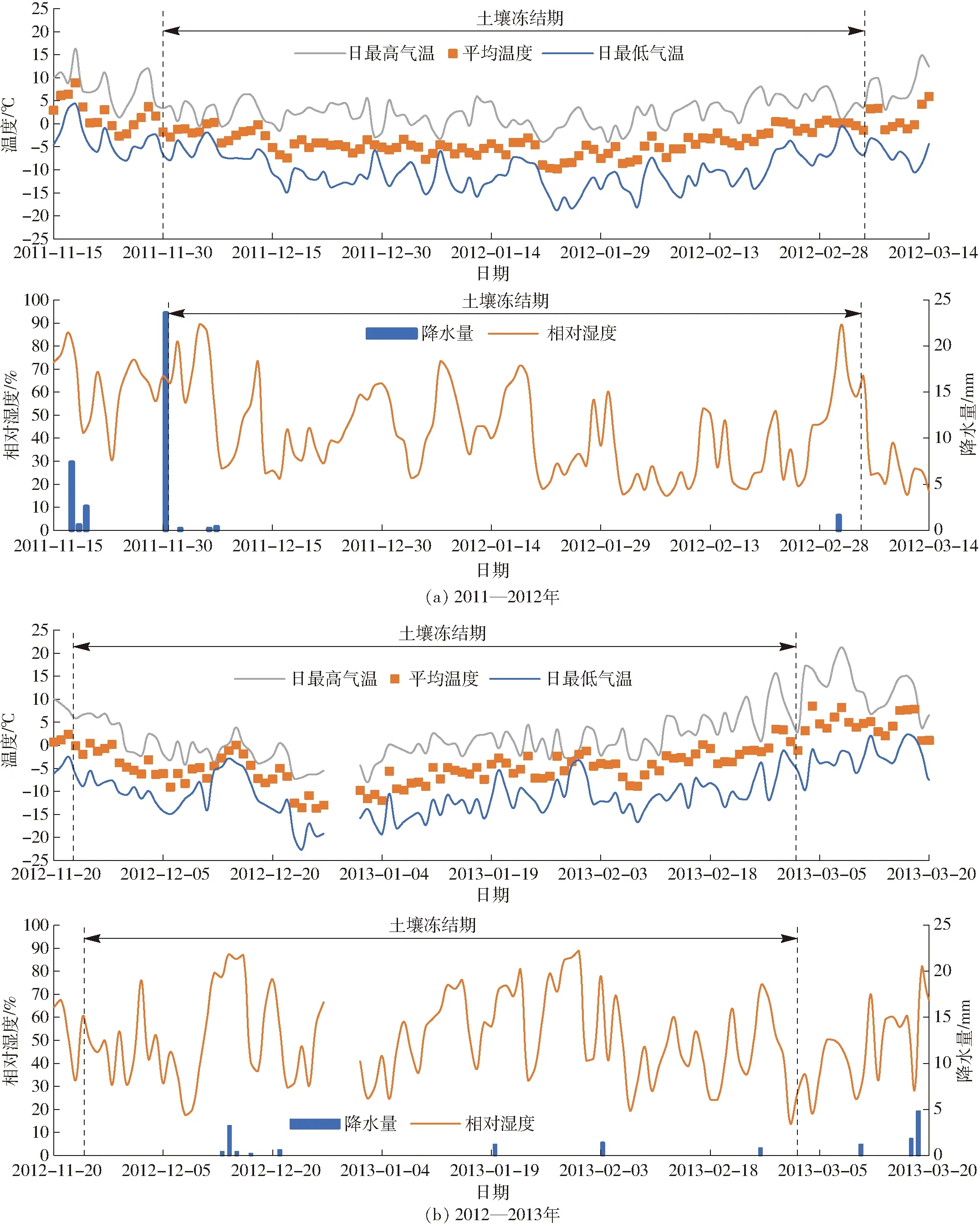
图1 2011—2012年和2012—2013年冬季空气温度、相对湿度和降水量Fig.1 Air temperature, relative humidity and precipitation in winters of 2011—2012 and 2012—2013

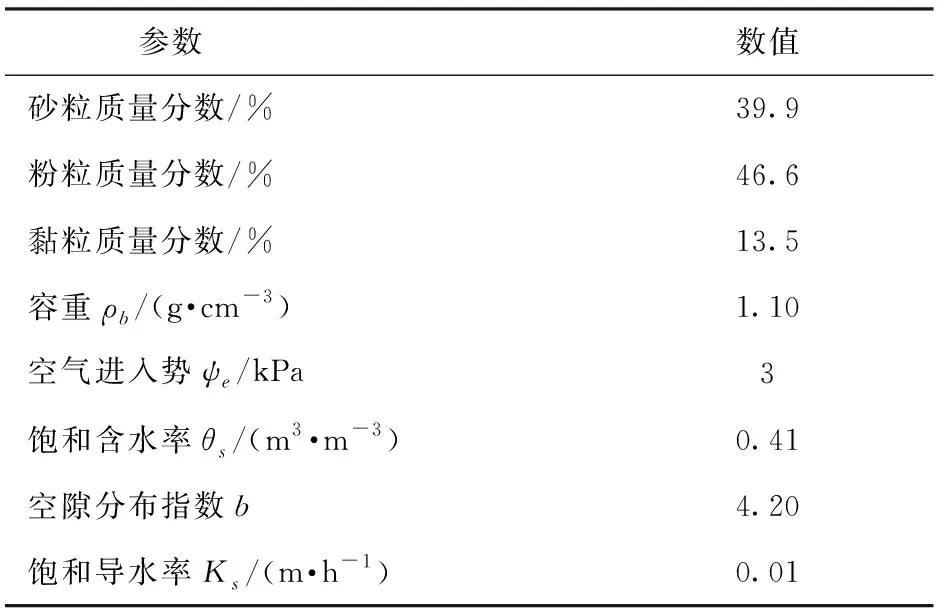
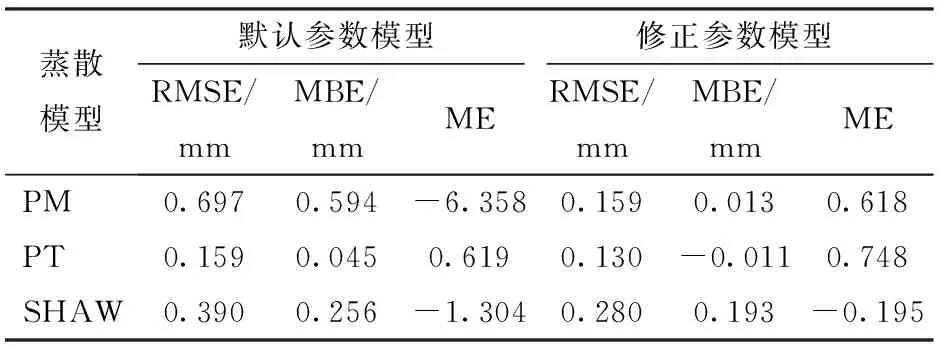
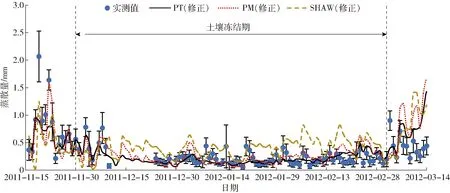
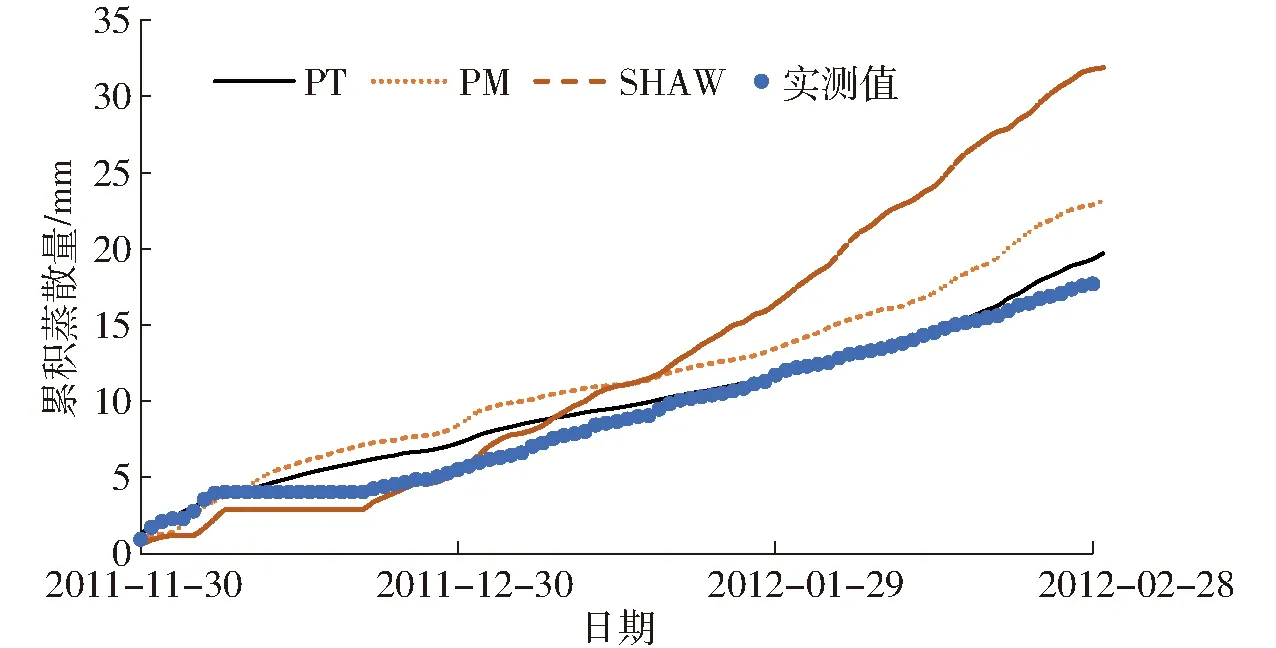
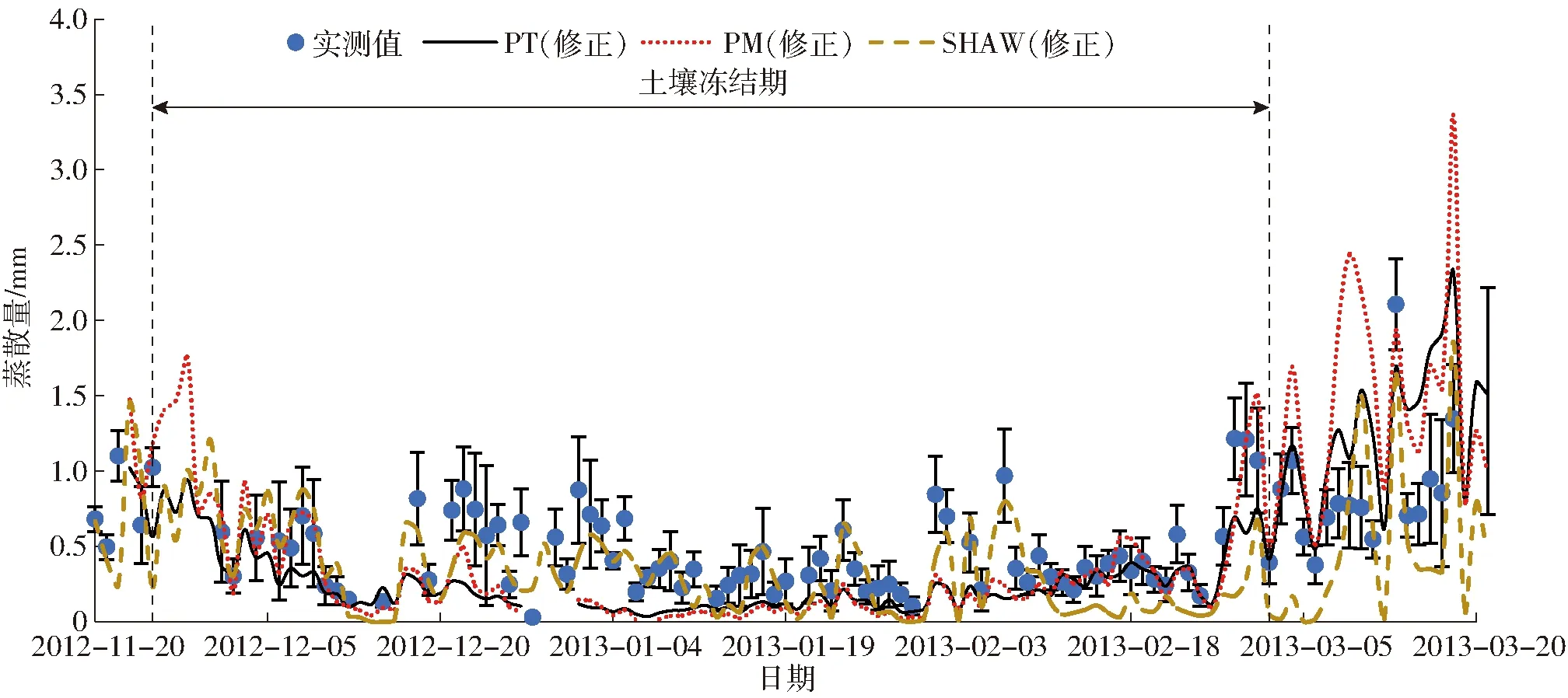
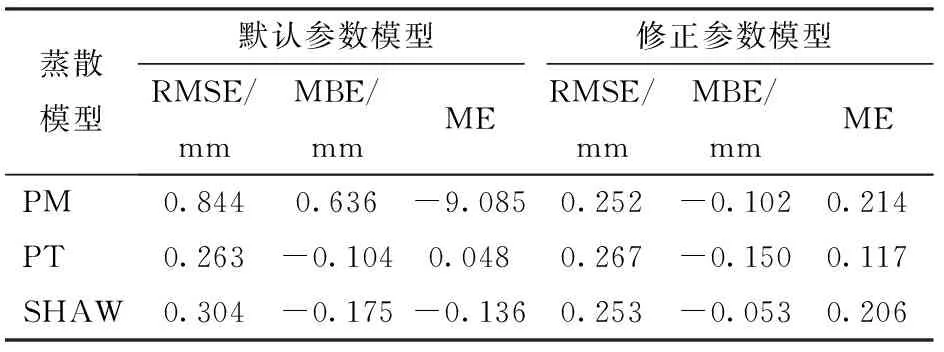
试验所用蒸渗仪数据为24套中型蒸渗仪(长1 m，宽0.75 m，深2.3 m；如图2所示)测量的平均值和标准差。每套蒸渗仪采用杠杆式称重系统，在利用平衡块抵消土箱和土质量后，使用质量传感器测量土壤中水分质量，以反映土壤蒸发量的变化[28]。传感器测量频率为每15 min一次，灵敏度为0.05～0.10 mm。本文对24组试验数据的平均值与模型估算值进行比较，并对试验数据进行相关性分析，结果显示：在显著性水平α=0.001的情况下，组与组之间相关系数R(0.339 2

SHAW模型的输入条件除气象条件外，还包括土壤剖面的初始含水率和初始温度。在本试验中，采用介电管式传感器测量土壤中的液态水含量，DS18B20型温度传感器测量土壤温度[29]。

2 结果与讨论

2.1 2011—2012年越冬期蒸散模型修正前后数据对比

将气象数据代入PM、PT、SHAW模型分别计算地表蒸散量(冬季只考虑土壤蒸发量)，结果如图3所示。从图中可以看出，在越冬期土壤冻结时，PT模型和SHAW模型的计算结果与蒸渗仪的实测值较为接近，根据误差分析结果(表2)可得，PT模型的RMSE最小，为0.159 mm，SHAW模型次之，PM模型最大。根据MBE值，可以看出3个模型相对于越冬期地表蒸散量的实测值均高估，这是由于越冬期土壤温度降低，土壤中部分液态水冻结成冰，减少了液态水含量，降低了土壤的基质势，使土壤环境形成水分胁迫状态，导致实际蒸散量低于无水分胁迫状态。为此，可引入水分胁迫系数KS减小土壤含水率对蒸散量估算值的影响，以提高模型精度。

表1 试验区土壤参数Tab.1 Soil parameters in experimental field

图2 蒸渗仪测量系统Fig.2 Lysimeter measurement system

图3 2011—2012年越冬期蒸散模型修正前数据对比Fig.3 Comparison of evapotranspiration before revising model in wintertime of 2011—2012

表2 2011—2012年越冬期蒸散模型修正前后误差分析Tab.2 Analysis of error before and after revising model in wintertime of 2011—2012

图4 2011—2012年越冬期蒸散模型修正后数据对比Fig.4 Comparison of evapotranspiration after revising model in wintertime of 2011—2012

本文利用蒸渗仪测得的蒸散量实测值与PM、PT模型得到的估算值进行比较，利用线性函数拟合出KS与土壤液态水含量θ之间的关系(表3)，使估算值的RMSE最小来优化参数。经过参数修正，PM模型的RMSE由0.697 mm降至0.159 mm，ME由-6.358增加到0.618，模型精度明显提高；在3个模型中PT模型的RMSE最小，为0.130 mm，ME最接近1；SHAW模型中的土壤反射率与蒸发量密切相关[30]，该参数增大时，误差相对减小，当调至最大值0.5时，RMSE减小为0.280 mm，但是由于SHAW软件的参数数值范围限制，不能继续优化数据以达到更好的修正效果(表2，图4)。3种模型经过参数修正后的蒸发累积量与实测值相比，PT模型的精度最高，SHAW和PM模型的累积量均高估(图5)。

表3 越冬期蒸散模型修正前后参数Tab.3 Parameters of evapotranspiration model before and after revising in wintertime

图5 2011—2012年修正蒸散模型越冬期累积蒸散量Fig.5 Cumulative evapotranspiration after revising model in wintertime of 2011—2012

通过误差对比发现，3种模型使用默认或经验参数进行估算，PT模型的估算精度最高。参数修正后，3种模型的估算精度都明显提高，且PT模型的估算精度仍然最高。PM模型默认参数误差较大，不适用于土壤冻结期的蒸发量计算，参数修正后模型精度大幅提高，证明了在冬季土壤冻结期内使用PM模型时考虑水分胁迫影响的重要性。SHAW模型的修正由于受到软件参数设定的限制，精度虽有所提高，但是与PT模型相比还存在一定差距，SHAW模型需要的参数繁多且复杂，实际计算难度较大，除了需要气象数据，还需要对土壤的相关参数进行测量，不仅提高了成本，而且测量过程中的误差也可能导致计算结果不准确。因此，为保证模型精度和降低成本，应当优先考虑使用PT模型。

2.2 2012—2013年越冬期蒸散模型适用性检验

将2011—2012年蒸散模型参数修正结果用于2012—2013年的蒸散量估算，进行模型的适用性检验和评价。由图6、表4可见，修正后的3个模型均能够较为精确地跟踪蒸散量的动态变化，其中PM模型的精确度最高，RMSE为0.252 mm，ME为0.214(表4)。参数修正后PT模型和SHAW模型的精度均有所提高，但并不明显，而PM模型的误差大幅减小，模型精度明显提高，RMSE由0.844 mm下降为0.252 mm，ME由-9.085上升至0.214。

图6 2012—2013年越冬期蒸散模型修正后数据对比Fig.6 Comparison of evapotranspiration after revising model in wintertime of 2012—2013

蒸散模型默认参数模型修正参数模型RMSE/mmMBE/mmMERMSE/mmMBE/mmMEPM0.8440.636-9.0850.252-0.1020.214PT0.263-0.1040.0480.267-0.1500.117SHAW0.304-0.175-0.1360.253-0.0530.206

参数修正后，PM模型中考虑了土壤冻结时因液态水含量降低引起的水分胁迫对蒸散量估算的影响，大幅提高了模型估算精度。PT模型的估算值受温度影响较大，这是由于在冻结土壤中，温度与液态水含量关系密切[25]。在2012—2013年12月17—25日期间，PT模型出现明显的低估，这可能是由于12月13—17日期间连续降雪(图1b)，而且日平均温度开始上升，覆盖在土壤表面的积雪部分融化，地表蒸散量增加。

2年的误差分析结果显示(表2、4)：使用默认的模型参数估算越冬期地表蒸散量时，PT模型的精度最高，且计算最为简便，所需气象数据和参数均最少，为最佳预测模型。在模型参数修正后，PM模型精度明显提高，PM模型不仅考虑了辐射和空气温度对蒸散量的影响，还包含了空气动力学因素的影响，如风速、相对湿度等，从而减小某一种因素的极端变化对结果的影响程度，使预测结果更稳定；PT模型受温度等气象数据影响较大，但该模型所需数据少，计算简便，精度相对较高；SHAW模型的精度稳定，但是需要大量的气象和冻土数据，且计算过程复杂。

3 结论

(1)在越冬期麦田地表蒸散量估算过程中，使用默认参数的各个模型的精度从低到高依次为PM、SHAW、PT，其RMSE分别为0.697、0.390、0.159 mm。PT和SHAW模型适用于冬季地表蒸发量的预测。由于冬季地表冻结使液态水含量降低，土壤出现水分胁迫，从而导致PM模型精度较低，不适用于冬季地表蒸散量的预测。

(2)考虑到土壤冻结与未冻土壤脱湿过程的相似性，引入水分胁迫系数对PM模型进行参数修正。修正后，模型精度明显提高，RMSE由0.697 mm降至0.159 mm，模型效率由-6.358提高至0.618。相比之下，PT模型的预测精度相对最高，所需数据量少且计算简便，但是受空气温度等气象因素影响较大。SHAW模型本身即为冻融条件下模拟土壤水热、能量等运移的模型，精度相对较高。

(3)使用2012—2013年的数据进行模型验证，参数修正后3个模型精度均有所提高，且精度相差不大，PM模型精度最高。但是由于SHAW模型的复杂性以及PM模型对数据的高要求，建议计算越冬期地表蒸散量时，优先使用PT模型。