非稳定渗流期解析法在均质土坝浸润线确定中的应用

骆秀萍，易 平

(新疆兵团勘测设计院(集团)有限责任公司，新疆 乌鲁木齐 830000)

我国目前已修建了8.6万余座水库，其中约有93%属于土石坝[1]，近年来，许多中小型水库陆续出现不同程度的病险问题[2]。根据土石坝工程安全事故统计数据显示，其中有37.1%的安全问题是由渗透变形引起的，因此研究土石坝渗流安全是水库大坝尤其是土石坝的重要安全问题之一[3]。水流通过坝体和坝基时存在压力和梯度，坝体、坝基渗漏量过大不仅会使水库产生损失、降低水库效益，还会造成坝坡失稳、坝体和坝基发生渗流破坏的安全隐患，而土石坝浸润线是大坝渗流量计算及坝坡抗滑，抗震，抗渗能力复核的重要依据[4-5]，因此，正确确定大坝浸润线对水库大坝进行渗流计算，对保障大坝安全稳定运行和提高工程效益具有重要的现实意义[6]，特别是当库水位下降时，大坝渗流形成非恒定流，坝体内浸润线高于坡外库水位，较高的孔隙水压力和渗透力会使上游坝坡具有下滑趋势，甚至酿成滑坡事故[7]。因此，如何确定土石坝浸润线保证坝体稳定是实际工程中需要研究的重要问题。文章采用解析法确定均质土坝在非稳定渗流期的浸润线，对大坝安全运行具有一定的借鉴意义。

1 计算原则

当水库水位下降时，坝体空隙中所含的水分，一部分会从上游坡面逸出，导致坝体中的浸润线逐渐下降，但其下降速度滞后于库水位下降速度，从而形成非恒定渗流。此时大坝上游坡受到渗流作用力，稳定性减弱。尤其当水库水位骤降时，渗流作用力变大，再加上孔隙压力的影响，就有可能导致上游坡失稳，发生坍塌，因而在重要的工程设计中，需要对非稳定渗流期大坝上游坡的稳定性进行校核。

目前为止严格求解非稳定渗流期大坝浸润线尚无具体方法，故常采用近似的简化方法进行处理[8]。对均质土坝，通常将k/μv(k为渗流系数，μ为土的排水系数，v为库水位下落速度)作为判别浸润线滞后于库水位下降的一个判别指标，当0.120～100时，浸润线与库水位接近同步下降，可不考虑库水位下降时对坝坡稳定的不利影响。

2 基于解析法的浸润线位置确定

2.1 初始渗流参数的确定

非稳定渗流在进行大坝渗流计算时，初始条件会对计算结果产生重大的影响，因此如果没有较为统一、合理的初始条件，非稳定渗流的计算结果就难以具有合理性、比较性和实用性[9]。当均质土坝(设排水棱体)位于不透水地基上，初始时(t=0)可近似认为恒定渗流浸润线逸出点在下游水位与棱体内坡的交点处。浸润线方程为：

图1 大坝渗流计算参数示意图

表1 土类系数表

(1)

l=d-m1H

(2)

(3)

其中：

(4)

(5)

式中，h0—初始时的浸润线高度。

各参数l，H1，H2，d，m1，l1，Δl如图1所示。

初始时的单宽渗流量为：

(6)

当水库水深由初始时的H1以速度v(作常数考虑)下降到时刻为t的h1时，浸润线在上游坡的出渗高度hB由下式计算：

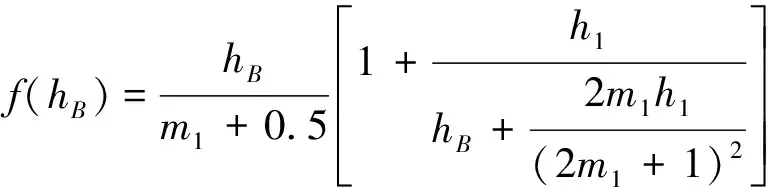
(7)

其中：

(8)

lt=l+m1(H-h1-hB)

(9)

p(n)为函数，可查水力计算手册确定。其中：

(10)

式中，k—坝身渗流系数；μ—坝身排水系数，μ=αp；p—土的孔隙率；α—系数，可由表1确定。

式(7)中，F(λτ，n)为函数，可查水力计算手册确定。

λτ由式(11)计算：

(11)

2.2 出渗高度的计算

采用试算法确定hB值，然后用此hB值分别由式(8)～(11)及查水力计算手册可求出H0，lt，n，λτ，p(n)及F(λτ，n)值，当库水位降至水深h1时根据下式计算浸润线：

(12)

y=x+m1(H-h1-hB)

(13)

式中，F(λ，n)—查水力计算手册确定。

其中：

(14)

由上可见，根据已知的k,μ，h1，t值并结合2.1节已求出的各个参数值，给定不同的x值，便可相继由式(13)可求得不同的y值，代入式(14)可得相应的λ值，查水力计算手册可得相应F(λτ，n)值，从而可根据式(12)便可求得水库水位降落后坝体内不同水平位置处浸润线的高度，即为所求浸润线。

3 工程实例验证

某水库为均质土坝，坝基不透水，坝高25m，上游坡坡比1∶3.0，下游坡坡比1∶2.0，下游坡设置排水棱体，库水位在4d时间内自H1=22m以速度3m/d下降至h1=10m，下游水位H2=4m保持不变，坝体渗流系数为2.2m/d，坝身排水系数μ=1，利用解析法计算大坝在初始水位及水位降落后的浸润线，计算结果见表2和表3。

表2 初始浸润线

水位降落初始浸润线及降落后浸润线如图2所示。

4 结论

合理确定土坝浸润线的位置，对坝体断面设计及渗流计算有重要影响。水库水位降落时坝体内渗流情况复杂，解析法可准确确定大坝在非稳定渗流期的浸润线，对工程设计具有指导意义。

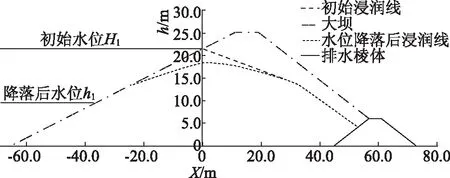
图2 非稳定渗流期水库浸润线