基于脉搏波特征参数的无创血压测量改进算法
瞿诗华,吴华炜,钱志余,李韪韬
(南京航空航天大学自动化学院,南京 211100)
1 引 言
连续无创的血压测量具有重要的临床应用价值,利用脉搏波特征参数连续无创测量血压的方法受到广泛关注。
张继光等人对单一对象提取脉搏波特征参数,分析脉搏波特征参数与血压之间的相关性,利用高相关性的特征参数建立血压计算模型。最终模型在计算该对象的血压时精度较高[1],满足AAMI标准[2],但是计算其他对象的血压时无法保证计算精度。颜国栋等人借助脉搏波特征参数并利用60人的脉搏波频域特征参数和对应的血压数据建立了血压计算模型[3],最终模型的计算结果误差满足AAMI标准,但是模型的计算对象均来自于正常人群的血压值,并未对病理情况下血压异常的人群进行实验和分析,在计算高血压或者低血压患者的血压时误差较大。因此,目前基于脉搏波特征参数测定血压的算法都缺乏普适性。
针对此问题,本研究提出了一种基于脉搏波特征参数的改进算法,算法利用相关性分析(correlation analysis,CA)去除无关特征参数,利用主成分分析(principal component analysis,PCA)对特征参数矩阵降维减少计算复杂度,利用多元线性回归建立脉搏波计算血压的模型。基于较大的数据库建立多级血压计算模型,并根据逐步逼近的原理[4],使每一级模型的计算结果逐步接近真实值,最终建立基于脉搏波特征参数计算血压的普适算法。
2 实验过程
2.1 数据采集与分组
实验需要采集多组脉搏波和血压数据,脉搏波数据是由光电血氧探头采集到的光电容积脉搏波(photoplethysmography,PPG)[5],血压数据采用水银血压计测得。数据采集过程在南京军区总院和江苏省人民医院心血管内科进行,医院主要采集血压异常人群,之后采集多组正常人数据作为数据库中正常人的数据样本。
采集PPG信号的长度定为1 min,设备的采样频率为100 Hz。采集PPG信号前被试者静坐5 min,采集过程中被试者保持平静[6]。采集完PPG信号后立刻测定被试者血压,保证采集数据的时间对应性。采集血压时连续测量被试者血压3次,取平均值作为血压参考值。
实验最终采集到了700个志愿者的血压和脉搏数据,为保证建立模型的准确性,实验最终在700组数据中分别选取了100名高血压(收缩压高于140 mmHg且舒张压高于90 mmHg)样本,100名低血压(收缩压低于90 mmHg且舒张压低于60 mmHg)样本和100名正常人样本组成数据库,保证数据库中各种类样本数相同。数据库中300名志愿者的年龄介于20~70岁,各年龄段样本数基本一致,且男女比例均衡。最终数据库内的收缩压跨度为83~198 mmHg,舒张压跨度为49~115 mmHg。
数据库中的300组数据按如下标准被均分到样本集和验证集中:
(1)各个类型的样本(高血压、正常和低血压)在两个集合中平均分配;
(2)样本集的血压范围跨度大于验证集的血压范围跨度。
按照以上标准分配后,最终样本集中收缩压跨度为83~198 mmHg,舒张压跨度为49~115 mmHg,验证集中收缩压跨度为87~186 mmHg,舒张压跨度为52~106 mmHg。样本集和验证集中高血压、正常人和低血压的样本数均为50组。
2.2 脉搏波预处理和特征参数提取
脉搏波预处理在matlab中进行,利用小波分解和重构的方法去除波形的基线漂移和高频噪声后得到良好的脉搏波信号[7-8]。通过寻找波峰和波谷的算法找到波形中的所有峰谷点后,提取出单个周期的脉搏波波形(见图1)。
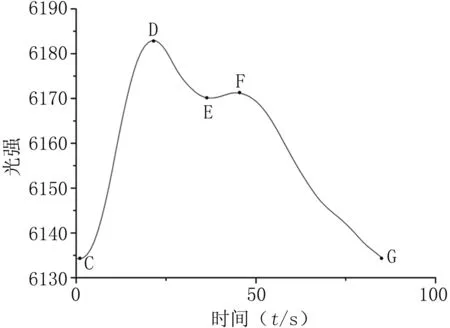
图1 单个周期的脉搏波波形
实验中需要提取的脉搏波特征参数包括时域特征参数和频域特征参数。
时域特征参数根据图1中脉搏波的特征点提取,图1中特征点各自的含义是:C为脉搏波周期起始点,D为脉搏波波峰,E为脉搏波重搏波起始点[9],F点为重搏波达到最大时的点,G为脉搏波下周期的起始点。C到D为脉搏波上升支,D到G为脉搏波下降支。由于重搏波谷点在部分志愿者的脉搏波波形中不明显,最终提取到的时域特征参数包括:脉搏波波谷光强值、脉搏平均强度(C点到G点所有点的平均光强值)、脉搏波波峰光强值、峰下面积、峰谷差值、下降支峰谷连线斜率(D点与G点连线的斜率)及脉宽(C点与G点横坐标差值)。
脉搏波频域特征参数在脉搏波的幅值谱中提取。在对单个周期的脉搏波波形进行10次周期延拓后,对延拓后的波形进行快速傅里叶变换得到脉搏波幅值谱见图2。
研究表明,脉搏波的频谱成分主要集中在基波到5~6次谐波内[10],最终实验提取的频域特征参数为脉搏波幅值谱中基波到第六次谐波这7个波峰对应的频率和幅值。
由于1 min的脉搏波信号包含多个脉搏周期,实验中对每个脉搏周期均提取上述21个特征参数得到多组特征参数,然后计算每个特征参数的平均值,利用平均值组成最终的特征参数向量。
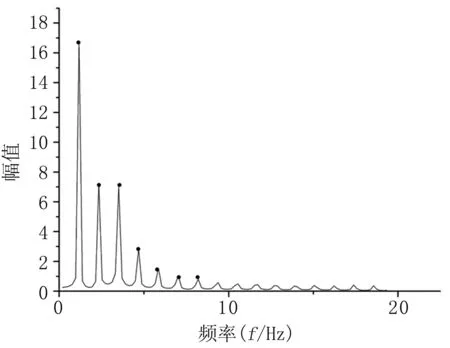
图2 脉搏波幅值谱
3 算法设计
3.1 确定血压计算模型
对300名志愿者中的每个样本按2.2中的方法提取脉搏波特征参数向量,将300组特征参数向量组成300×21的特征参数矩阵R,同时将每个志愿者对应的真实收缩压和舒张压分别存入向量ySBP和yDBP中,利用分别和ySBP与yDBP做相关性分析得到各特征参数与收缩压和舒张压的皮尔森相关系数[11-12],结果见图3和图4。
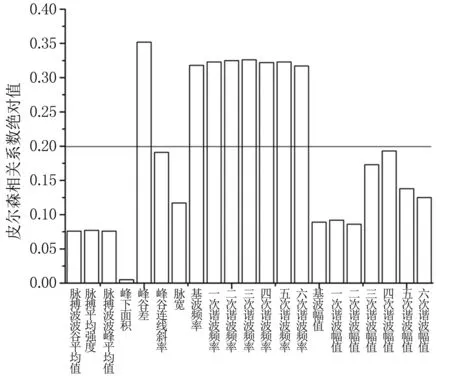
图3 脉搏波各特征参数与收缩压之间的
由于两变量之间的皮尔森相关系数绝对值不小于0.2时变量之间具有相关性,小于0.2时不具相关性[13-14]。因此,最终计算收缩压的特征参数矩阵大小为300×8,计算舒张压的特征参数矩阵大小为300×20,将前后两个矩阵记为RPCAS和RPCAD。RPCAS和RPCAD维数较高,利用PCA进行降维处理来减小计算的复杂度。分别对RPCAS和RPCAD做主成分分析,得到两个矩阵中各个主成分的特征值[15],见图5和图6。
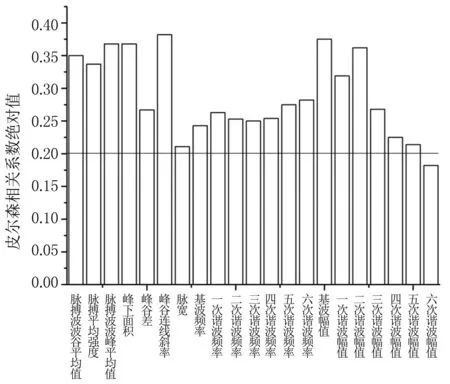
图4 脉搏波各特征参数与舒张压之间
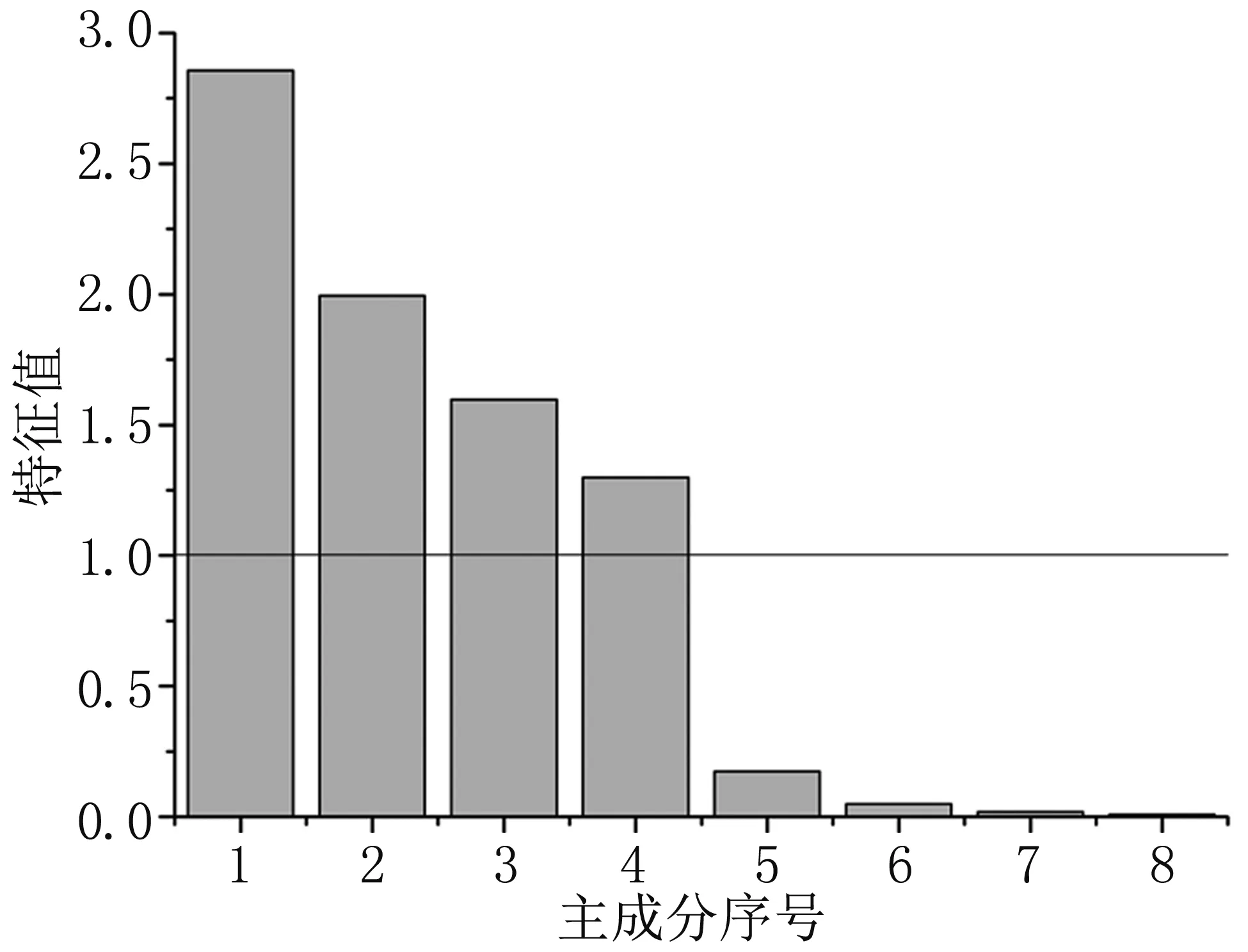
图5 矩阵RPCAS中各主成分的特征值
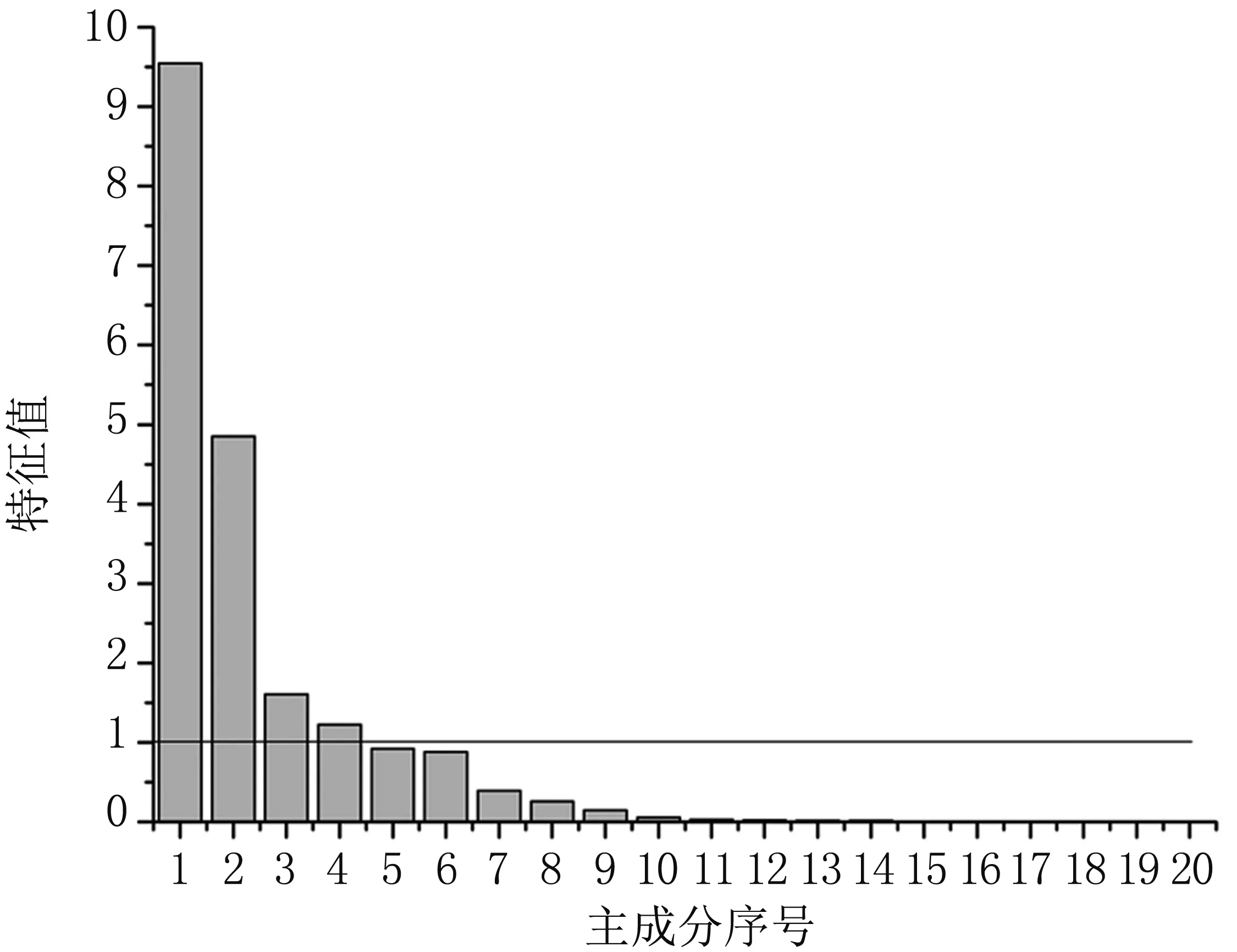
图6 矩阵RPCAD中各主成分的特征值
选取特征值大于等于1的主成分[16],因此,计算收缩压和舒张压的主成分矩阵均为4维矩阵,分别记为:
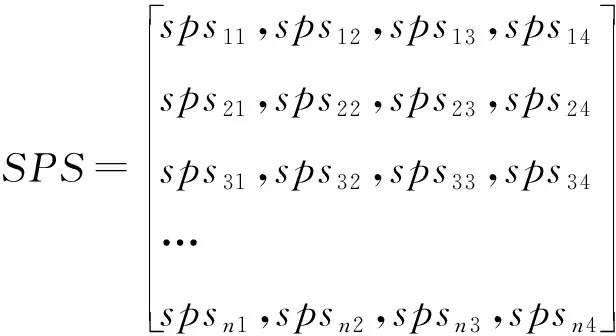
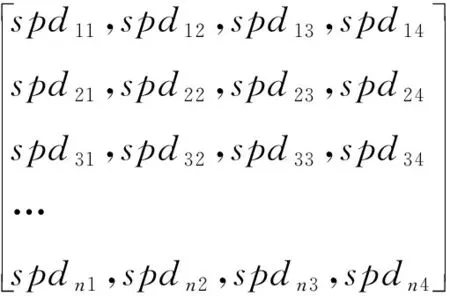
以SPS作为自变量,ySBP作为因变量进行多元线性回归分析得到收缩压的回归系数[17-18]为:
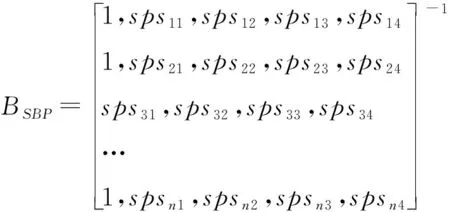
(1)
以SPD作为自变量,yDBP作为因变量进行多元线性回归分析得到舒张压的回归系数为:
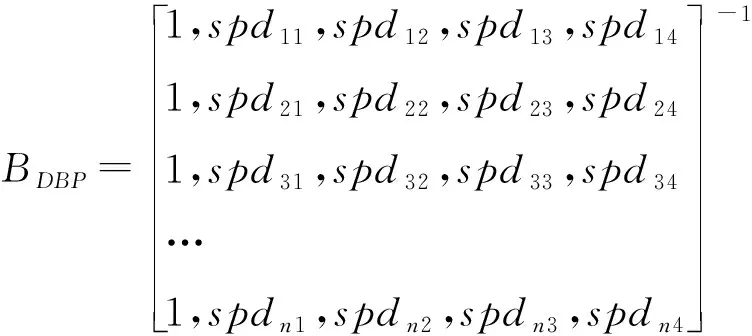
(2)
两者均为5×1的矩阵。对任意志愿者ω提取其主成分参数向量W=[w1,w2,w3,w4]后,利用(1)式和(2)式得到其收缩压(BPS)和舒张压(BPD)的计算值分别为:
BPS=[1,W]·BSBP
(3)
BPD=[1,W]·BDBP
(4)
3.2 逐步逼近减小误差
以计算任意志愿者Zeta的收缩压为例,舒张压的计算方式与之一致,Zeta降维后的主成分参数矩阵记为Z=[z1,z2,z3,z4]。算法结构图见图7。
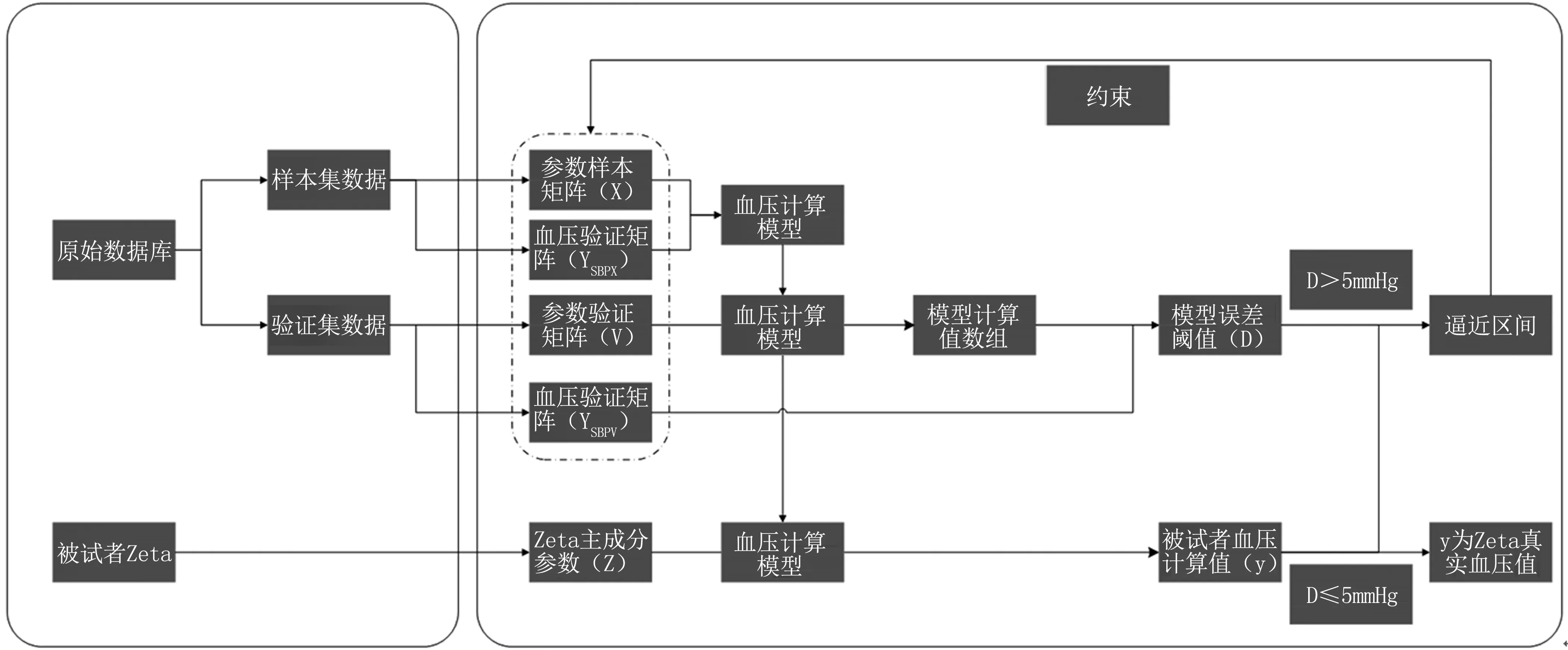
图7 算法结构图
具体计算过程按以下步骤进行:
第二步:将X1和YSBPX1代入(1)式得到一级回归系数:

(5)
将Z和B1代入式(3)计算出一级模型计算值:
y1=[1,Z]·B1
(6)
将B1和V1代入(1)式得到验证集中每个个体的一级收缩压计算值数组:
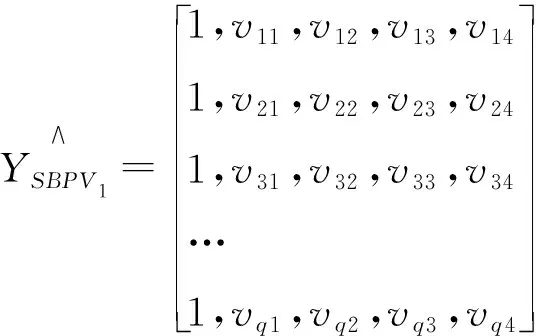
(7)
计算验证集的一级模型误差数组:
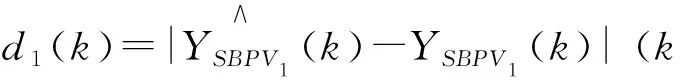
(8)
取出d1中的最大值记为一级模型误差阈值D1。
利用y1和D1确定Zeta真实收缩压所在的第一个区间A1:[y1-D1,y1+D1],记为一级逼近区间[19]。并利用A1计算二级参数样本矩阵X2、二级参数验证矩阵V2、二级血压样本矩阵YSBPX2和二级血压验证矩阵YSBPV2,具体方法如下:
(1)提取YSBPX1中属于区间A1的数据组成YSBPX2;
(2)提取YSBPV1中属于区间A1的数据组成YSBPV2;
(3)在矩阵X1内找到YSBPX3中各个元素对应的行向量,并将这些行向量按YSBPX2内的元素顺序组成二级样本矩阵X2,然后用同样的方法得到V2。
第三步:重复第二步的操作,利用X2、V2、YSBPX2和YSBPV2计算得到y2,D2、X3、V3、YSBPX3和YSBPV3
......
重复第二步的操作i次得到第i+1级模型的血压计算值yi+1和误差阈值Di+1,如果Di+1≤5 mmHg,则认定yi+1为被试者Zeta的血压值,若不满足则利用Xi+2、Vi+2、YSBPXi+2和YSBPVi+2进行下一级运算,直至Di+j≤5 mmHg(j≥2且j为整数),如果Di+j无法缩小到5 mmHg以内,则运算过程中必然会出现Di+f=Di+f+1(f≥j),此时输出从第1级模型到第i+f+1级模型的所有血压计算值和对应的模型误差阈值作为分析依据,用以改进算法。
4 实验结果
随机选取数据库外的10名志愿者,利用本研究算法计算血压,计算终止时用到的模型级数和对应的模型误差阈值见表1、表2。
表1不同测试者的收缩压计算结果
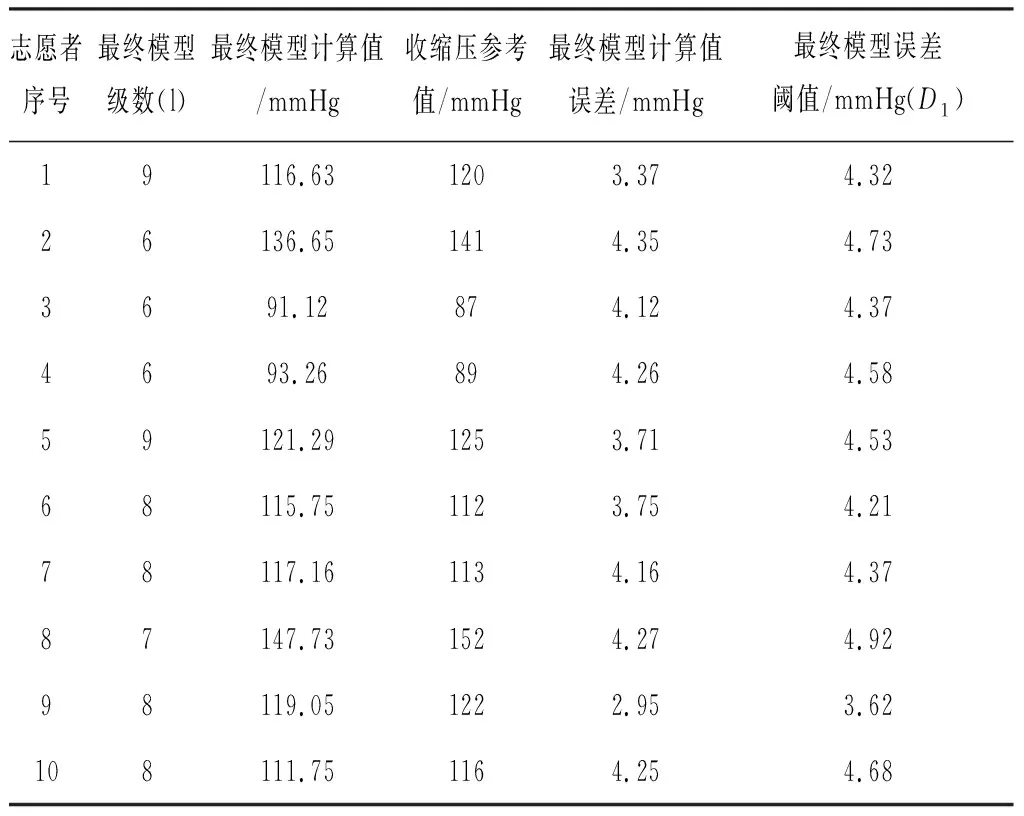
Table 1 Calculation results of systolic pressure for different subjects
表2不同测试者的舒张压计算结果
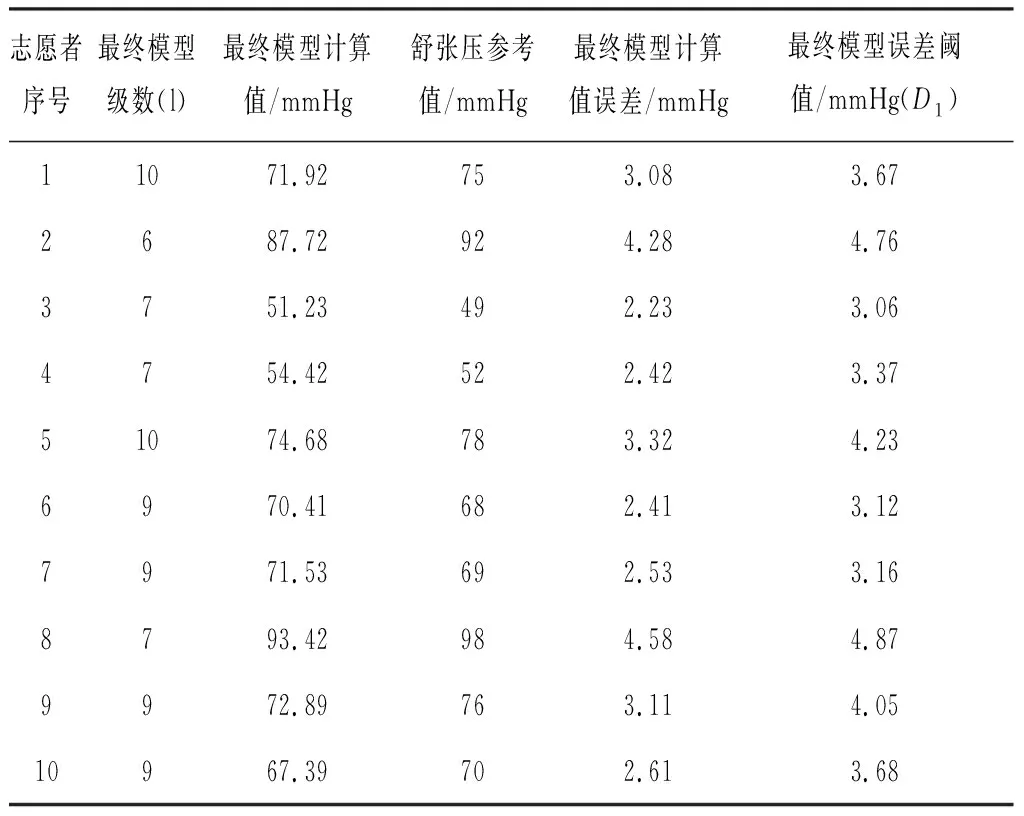
Table 2 Calculation results of diastolic pressure for different subjects
分析表1和表2,10名志愿者的收缩压和舒张压的最终模型计算值误差均达到5 mmHg以内,优于AAMI标准。再分析10名志愿者的血压分布情况,10名志愿者中有2名高血压患者(2号和8号),2名低血压患者(3号和4号)及6名血压正常的人。本研究提出的算法最终对这10名志愿者均能准确计算收缩压和舒张压,而且计算精度优于AAMI标准。因此,本研究提出的改进算法解决了基于脉搏波特征参数无法建立普适的血压测量模型的问题,能够应用于计算包括病理血压值在内的血压。
5 总结
脉搏波波形比较复杂,目前还无法揭示它和血压之间的内在联系[20]。利用脉搏波精确计算血压并且建立普适性高的血压计算模型是目前研究遇到的主要问题。本研究提出的改进算法通过建立大型数据库,利用线性回归建立脉搏波特征参数和血压之间的初步计算模型,然后层层递进通过缩小线性回归用到的样本区间建立更加准确的计算模型从而增加计算精度,最终建立的模型适用于包括高血压、正常人及低血压在内的被试者,实现了普适的基于脉搏波特征参数的无创血压测量。

