考虑非线性振型的顺风向广义气动力谱

李阳阳，李建成，冯松宝*，孙 磊，麻洪蕊，张萍花

(1.宿州学院 资源与土木工程学院, 安徽 宿州 234000；2.湖南大学 建筑安全与节能教育部重点实验室, 湖南 长沙 410082)

0 引言

20世纪50年代初期，建筑物一般不高，外形简单规则且楼层的质量和刚度沿高度方向分布均匀，结构的基本振型可以认为是理想的线性振型.相应地,为了计算方便，在顺风向阵风荷载因子法以及高频底座天平技术等传统计算结构风致响应的方法也均是以此为假设，这些方法在应用于具有理想线性振型的结构时，简单实用且准确度较高[1].

然而，近年来随着社会经济的快速发展，部分建筑的质量和刚度由于沿高度方向呈现不均匀的分布或其他原因已不再满足理想的线性振型，即在顺风向的模态振型沿高度方向不再满足线性变化而呈现出非线性.以结构第一阶振型为线性振型的假设，当出现非线性振型情况时，阵风荷载因子法以及高频底座天平技术难免会出现较大误差.

在顺风向，许多国内外学者研究了非线性振型对高层建筑广义气动力谱的影响.VICKERY等[2]以某一实际建筑物为例发现，根据理想线性振型计算得出的广义气动力谱出现了1%～2%的误差，同时对阵风荷载因子法给出了一个简单的修正公式.周印等[3]指出了非线性模态振型对高层建筑风振背景响应和共振响应的敏感性不同且不可忽略.XU等[4]基于风洞试验数据，提出了顺风向的广义气动力谱修正公式.BOGGS等[5]假设在高度方向风荷载呈现完全的相关性，系统地分析了非线性振型对基础底部的弯矩、结构顶部的位移和加速度的影响.HOLMES等[6]将风力谱密度沿高度变化的相关性细分为低相关和高相关，分别计算出了非线性振型对于风荷载的修正公式.考虑到非线性振型对高频底座天平技术的影响，澳大利亚标准AS1170.4给出了对应于基础底部弯矩的修正公式0.76+0.24β，β是第一阶模态振型指数[7].

本文则以此为出发点，在顺风向，结合不同的平均风速剖面指数α，研究非线性振型对广义气动力谱的影响，并给出关于振型指数β的修正公式，以提升阵风荷载因子法以及高频底座天平技术等传统方法计算结构风致响应的准确性.

1 广义气动力谱修正公式

1.1 基本公式推导

由文献[8]可知，在顺风向根据随机振动的理论，并基于如下假设：

(1)准定常假设.

(1)

式中：w(z,t)、(z,t)分别为建筑某一点z高度处t时刻的风压和风速，ρ为空气密度，CD为阻力系数.

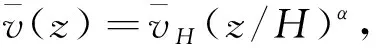
(2)

式中：H为建筑总高度，α为平均风速剖面指数.

(3)阻力系数沿建筑高度不变

Cd(z)=CD.

(3)

由此可得，作用在建筑物上的第一阶广义气动力谱密度SF1(n)，假设不计振型之间的耦合作用时，其为：

Rxz(M1,M2,n)dxdx′dzdz′,

(4)

第一阶振型φ1(z)采用幂函数表示，振型指数为β，表达式如下：

(5)

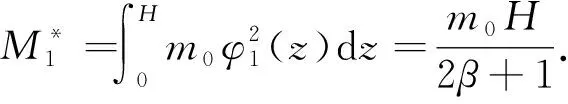
(6)

脉动风速相干函数Rxz(M1,M2,n)采用Shiotani相关函数，如下所示：

Rxz(M1,M2,n)=Rx(x,x′)Rz(z,z′),

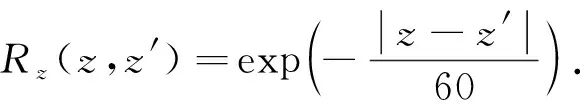
(7)

将式(5)、(6)和(7)代入式(4)，可得：

FJZ(α,β)2Jx(B)2,

(8)

式中：JZ(α,β)2、Jx(B)2分别定义为竖向和水平向的结合函数.

由式(8)可知，对于理想的线性振型，即振型指数β=1，其广义气动力谱密度为：

(9)

根据式(8)和式(9)，可得广义气动力谱的振型修正Φ为：

(10)

式中，JZ(α,1)2的表达式为：

(11)

式(10)中ΦM是广义质量的修正，一般而言，实际振型的广义质量比较容易计算，这里不做研究，本文只对广义气动力谱修正系数ΦD进行讨论计算：

(12)

1.2 参数分析

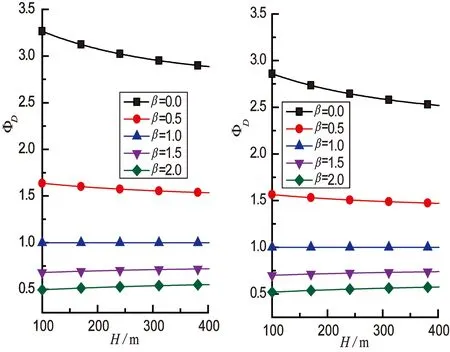
式(12)中各个参数的取值范围考虑如下：α取0.12、0.30，β取0～2，H取100～400 m.采用数值积分的方法，得到了公式(12)的数值，下面通过图形说明各个参数(α、β、H)对广义气动力谱振型修正系数ΦD的敏感程度.图1为修正系数随高度的变化曲线；图2为修正系数随振型指数的变化曲线.

(a) α=0.12 (b) α=0.30

从图1和图2可得出：

(1)对于固定的α、β值，随着高度H的增加，当振型指数β小于1时，修正系数ΦD逐渐变小，而振型指数大于1时，修正系数ΦD基本不变；对于固定的α、H值，随着振型指数β的增加，修正系数ΦD逐渐减小，且在β<1时，变化较大.

(2)修正系数ΦD关于振型指数β呈单调递减的非线性变化规律.当振型指数β小于1时，修正系数ΦD均大于1，此时实际振型的广义气动力谱是大于理想线性振型的广义气动力谱的，计算结果是偏于不安全的；反之，振型指数β大于1时，修正系数ΦD均小于1，这时高估了结构的广义气动力谱.β=1(理想线性模态)时，修正系数ΦD恒等于1.

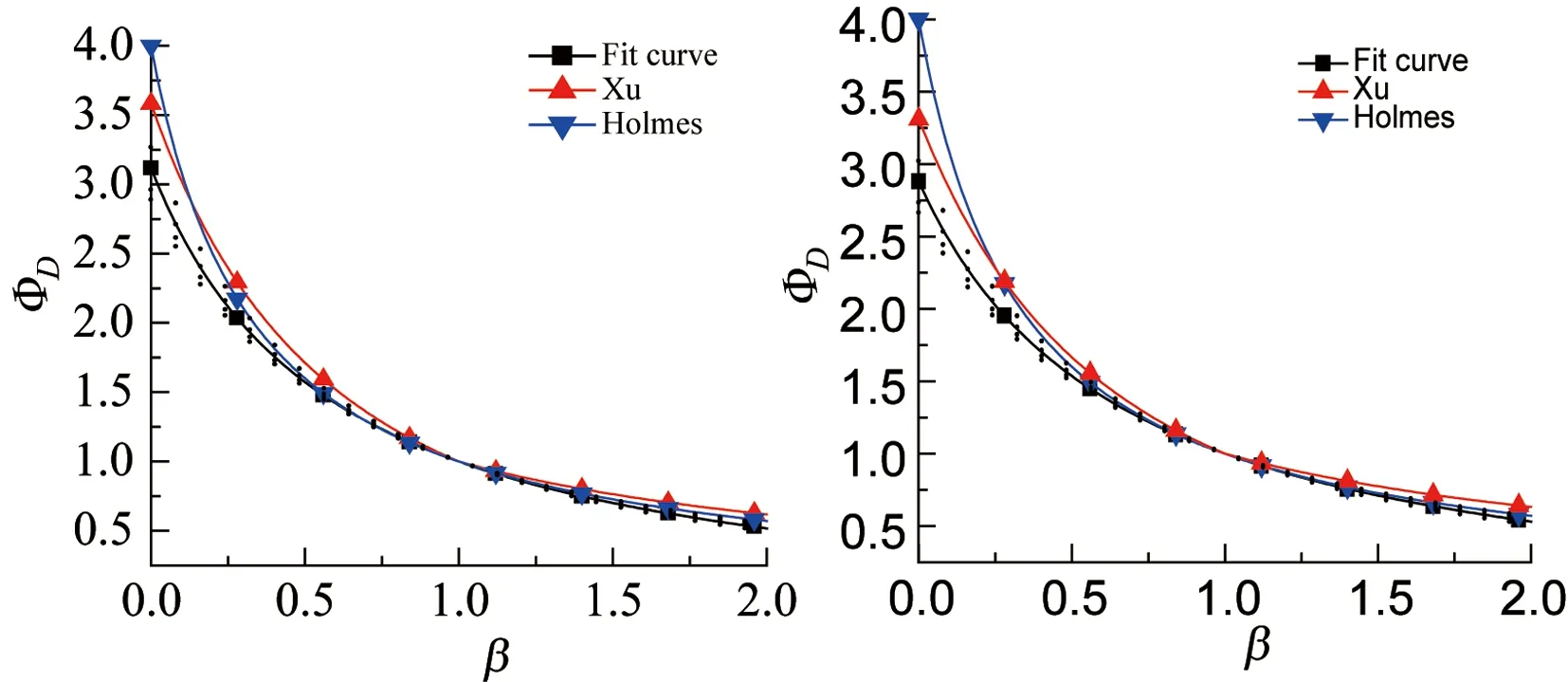
(3)在α=0.12、0.30，β=0～2，H=100～400 m的情况下，ΦD最大值为3.25，最小值为0.51，与线性振型假设下的“1”相比，误差较大，因此建议对非线性振型的顺风向广义气动力谱进行修正，以免过分保守或夸大地估算结构的风致响应.

(a) H=100 m (b) H=400 m

1.3 修正系数拟合

由式(12)可知，修正系数ΦD与参数α、β和H的取值均有关，本文计算时考虑了高度H的影响，但为了方便公式运用，在拟合公式时忽略了高度H的影响，其仅是α和β的函数.根据积分结果，式(12)最终拟合为：

(13)

图3给出了α=0.12和0.30时拟合公式的两种结果，图中散点代表计算数据，该数据根据公式(12)所得，取自1.2节所得数值.作为比较也展示了XU[4]和HOLMES[6]的修正曲线.从图3可看出，本文提出的拟合结果总体上与文献[4，6]接近，由于在计算时考虑了高度，图形上略有些不同.

2 基于规范振型的建议

由建筑结构荷载规范[9]可知，顺风向高层建筑的基本振型为：

(14)

式中，ξ=z/H为相对高度.采用幂函数的形式对规范振型进行拟合，得到其指数β=0.896，表达式如下：

φz=ξ0.896.

(15)

图4分别给出了规范振型和拟合振型的基本振型曲线，从图中可知，两者总体上差别不大，从而较好地保证了两者的统一性.

(a) α=0.12 (b) α=0.30

图4 基本振型曲线Fig. 4 The basic mode shape curve

根据分析可知，顺风向高层建筑的基本振型并非理想的线性振型(β=0.896≠1)且小于1.根据1.2节所得到规律，此时若按传统方法(阵风荷载因子法以及高频底座天平技术)估算结构的风致响应，就会出现计算值偏小的情况.

表1给出了当采用规范振型时，平均风速剖面指数α=0.12、0.15、0.22、0.30的具体广义气动力谱修正系数.由表1可知，修正系数的变化范围为1.080～1.088，简化起见建议取常数1.1进行修正.

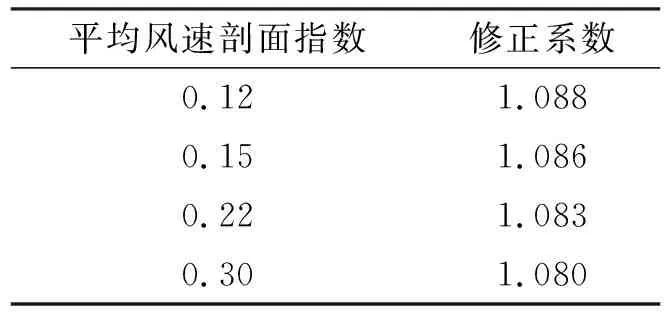
表1 线性振型的修正系数Tab. 1 Correction coefficient of the linear mode

3 修正公式结果验证

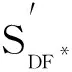
(16)

(a) β=0.5 (b) β=1.5

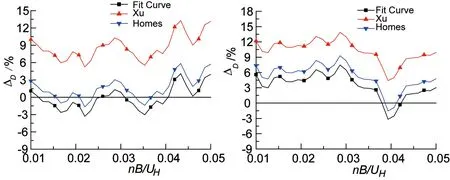
由图5可知，在顺风向，广义气动力谱密度的误差值ΔD随着频率的增加而变化.与XU和HOLMES的方法相比较：按本文方法修正的广义气动力谱密度与实际值相差甚少，相比于实际值，误差基本在-4%～8%之间，拟合情况良好.

4 结论

本文研究了非线性振型对于高层建筑顺风向广义气动力谱的影响，得到的主要结论如下：

(1)在顺风向，根据平均风速剖面指数α、建筑高度H以及迎风面宽度B，运用数值积分的方法，计算得到了振型指数为的β广义气动力谱与理想线性振型的广义气动力谱比值.同时，结合平均风速剖面指数和振型指数，拟合出了非线性振型的广义气动力谱修正公式，并通过风洞试验发现该公式拟合情况良好，修正如下：

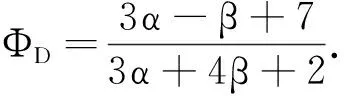
(17)

(2)在顺风向，当振型指数小于1时，修正系数大于1，也即此时实际振型的广义气动力谱大于线性振型的广义气动力谱，按传统方法计算的广义气动力谱偏小，计算结果是偏于不安全的；反之，当振型指数大于1时，此时对结构设计而言，按传统方法计算的广义气动力谱是偏于保守的.由此，基于线性振型得到的广义气动力谱，本文建议采用1.1的修正系数进行修正，可应用于建筑结构荷载规范所采用的振型.

(3)对于固定的α和H，修正系数ΦD随着振型指数β的增大而逐渐减小，且在β小于1时，变化较大.对于固定的α和β，当振型指数β小于1时，修正系数ΦD随着高度H的增大而逐渐变小，而振型指数大于1时，修正系数ΦD基本不变.