An extended J-integral for evaluating fluid-driven cracks in hydraulic fracturing

Huifang Song,Sheik S.Rahman

School of Petroleum Engineering,University of New South Wales,Sydney,2052,Australia

Keywords:Extended J-integral Three-dimensional(3D)point-wise J-integral Crack tip behavior Hydraulic fracturing Path-independence

A B S T R A C T J-integral has served as a powerful tool in characterizing crack tip status.The main feature,i.e.pathindependence,makes it one of the foremost fracture parameters.In order to remain the pathindependence for fluid-driven cracks,J-integral is revised.In this paper,we present an extended J-integral explicitly for fluid-driven cracks,e.g.hydraulically induced fractures in petroleum reservoirs,for three-dimensional(3D)problems.Particularly,point-wise 3D extended J-integral is proposed to characterize the state of a point along crack front.Besides,applications of the extended J-integral to porous media and thermally induced stress conditions are explored.Numerical results show that the extended J-integral is indeed path-independent,and they are in good agreement with those of equivalent domain integral under linear elastic and elastoplastic conditions.In addition,two distance-independent circular integrals in the K-dominance zone are established,which can be used to calculate the stress intensity factor(SIF).

1.Introduction

Parameters of stress intensity factor(SIF),crack tip opening displacement(CTOD),energy release rate and J-integral are most commonly used to evaluate crack geometry,stress field,stability state of fracture tip,etc.The usage and calculation of each of these parameters are often limited to certain conditions such as elastic materials,small-displacement assumption or small-scale plastic region.Among these parameters,J-integral,however,has been found to be the most effective method in characterizing fracture tip due to its wider application range.

J-integral is a path integral along the contour starting from any point on bottom surface of the crack and ending in top surface.It was initially proposed independently by Cherepanov(1967)and Rice(1968a)as an alternative approach to determine the energy release rate.The original form of J-integral is expressed as where w is the strain energy density,Γis the integral path from the bottom to the top surface around the crack,T is the traction along the path,u is the displacement vector along the path,and ds is the line element along the path.

Rice(1968a)showed that the value of J-integral is equal to the energy release rate during crack extension,regardless of its integration path.The path-independence made the J-integral a powerful tool to investigate a wide range of studies,such as different types of loading,material laws and field problems,in both linear elastic and elastoplastic conditions,especially in connection with numerical analysis.One of the main advantages of J-integral is that it can be calculated in a region far enough from crack tip so that the numerical accuracy is not compromised.In case of small-scale yielding,in which stress field beyond yield zone is still governed by stress singularity,Rice (1968a)showed that the path in dependent J-integral can be correlated to the SIF(KI)in mode-I fracture loading as follows:

where νis the Poisson’s ratio,and E is the Young’s modulus.In case of plane-stress condition,Eq.(2)applies by replacing 1-ν2with unity.Similarly,Eq.(2)can be generalized for mode-II and mode-III loading cases.

In case of elastoplastic conditions,J-integral is also capable of characterizing the intensity of the crack tip stress field.Therefore,the critical value of J-integral(Jc)plays a comparable role in determining fracture toughness in elastoplastic condition as critical SIF does in elastic condition(Kuna,2013).Landes and Begley(1977)proposed experimental procedures using a series of specimens to determine Jc.Subsequently,standard experimental procedure was developed(ASTM E1737-96;1996).Either a critical value or a resistance curve can be obtained by using particular standardized specimen(Tada et al.,2000)for a test material.J measurement is also a substitute where the value of SIF(K)is not available,especially when the plastic zone around the crack tip is too large.

Numerous attempts have been made in the literature to extend the applications of the path-independent J-integral.Begley and Landes(1972)applied the J-integral to determining the fracture toughness in elastoplastic materials.Their results were validated against experimental determination of JIC(for mode-I)through different measuring points(Landes and Begley,1974,1977).In addition,Landes and Begley(1976)proposed a modification of J-integral under nonlinear viscous flow rule,denoted as C*,in which strain and displacement were replaced by their time derivatives,respectively.Schapery(1984)developed a generalized J-integral which is applicable to a wide range of viscoelastic materials.By such modification,the application of J-integral was extended to high-temperature creep cracking phenomena(Taira et al.,1979).For bi-material interface crack problems,M1integral,another extended version of J-integral,was developed(Miyazaki et al.,1993).More relevant applications of J-integral have been continuously developed by different researchers(Roberti et al.,1984;Landis,2004;Prawoto and Onn,2012;Zimmerman and Jones,2013; Ochensberger and Kolednik,2014).

Apart from the application of the J-integral as fracture criterion,it also offers a potential characterization tool to study stress field in yield region.Stress field around crack tip under elastic assumption can be simply acquired from the SIFs KI,KIIand KIII,which were given by Irwin(1957)using Westergaard(1939)’s method.In reality,however,yield or plastic zone exists around crack tip and therefore,elastoplastic fracture mechanics needs to be considered to take into account the yield region.In order to address such effects,Hutchinson(1968)and Rice and Rosengren(1968)applied power-law deformation theory of plasticity and demonstrated that the near-tip stress field can be expressed as a function of J-integral.This near-tip area is called HRR field(HRR for initials of the authors),or J-dominance zone,as shown in Fig.1.It is noteworthy that the HRR field solution is applied under the assumptions of small strain,infinite plate,and monotonical as well as proportional loading since the deformation theory cannot be used when unloading occurs.

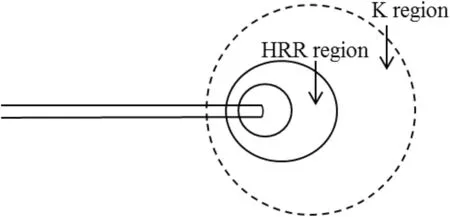
Fig.1.Stress variation ahead of the crack.

The numerical computation of J-integral,in particular with finite element method(FEM),has also been widely studied.J-integral can be calculated directly by interpolating the variables on predefined arbitrary path using numerical computation.Such an interpolative approach is,however,associated with uncertainty as stress magnitudes are calculated for Gauss points,whereas displacements are solved over nodal points.In order to address such an uncertainty,equivalent domain integral(EDI)(Hutchinson,1968;Li et al.,1985;Nikishkov and Atluri,1987;Raju and Shivakumar,1990)has been proposed to compute the J-integral value.EDI is a generalization of virtual crack extension method(Parks,1977,1978;deLorenzi,1982;Li et al.,1985),which essentially evolves from the calculation of energy release rate directly.The domain integration alleviates the local solution error.

The application of the J-integral to hydraulic fracturing needs further improvements as there are issues such as internal traction,porous media and,in some cases,thermal strain.It is noteworthy that hydraulic fracturing is a technique used to facilitate oil and gas extraction by creating cracks under induced fluid pressure and it is now an indispensable process in the development of tight gas and shale gas reservoirs.Karlsson and Bäcklund(1978)developed a revised J-integral for internally loaded cracks in two-dimensional(2D)cases.However,a more detailed extension for three-dimensional(3D)internally pressurized cracks and the cracks under thermal conditions are not available currently.

In this study,J-integral is further extended to make it suitable for investigating 3D hydraulically pressurized fractures and its path-independence is successfully examined.Conditions of porous media and thermal strains are discussed.The application of the extended J-integral is assessed and the results are compared against those obtained by the currently available methodologies.The main purpose of the proposed methodology is to apply the concept of J-integral to a much wider range of fracture treatments.

2.Formulation of 3D J-integral and its application to hydraulic fracturing

J-integral can be represented by the subtraction of its two components as follows:

Rice(1968a)indicated that J-integral values are equal along all paths around crack tip.This conclusion was derived based on conservative enclosed path,that is,for an enclosed path without singular point inside,J is proved to be zero.This statement was made based on the following assumptions:(1)strain-displacement relation is linear(small strain);(2)no body force exists;and(3)no singularity point exists along/within the integration line.A detailed derivation is shown in Appendix A.

Rice(1968a)suggested that J-integral is a measure of average strain energy of crack tip in the case of a blunt crack.In case of a sharp tip,the contour can shrink to as near as crack tip and yet not reaching the sharp tip:where r is the distance to the crack tip.

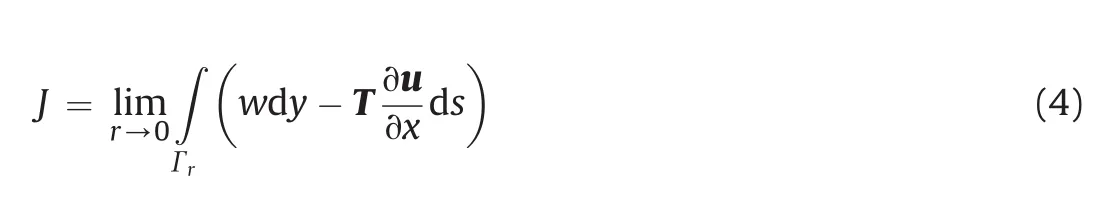
Therefore,we could consider that J-integral is a characterizing parameter of the crack tip field.From an energy point of view,J-integral represents the potential energy release rate.

Under linear elastic condition,J is related to KI,as shown in Eq.(2).By working out the integration of J,it is found that if the integration route is circular and within K-dominance zone,J1and J2are also distance-independent of crack tip,which can be used as an alternative technique to calculate KI:

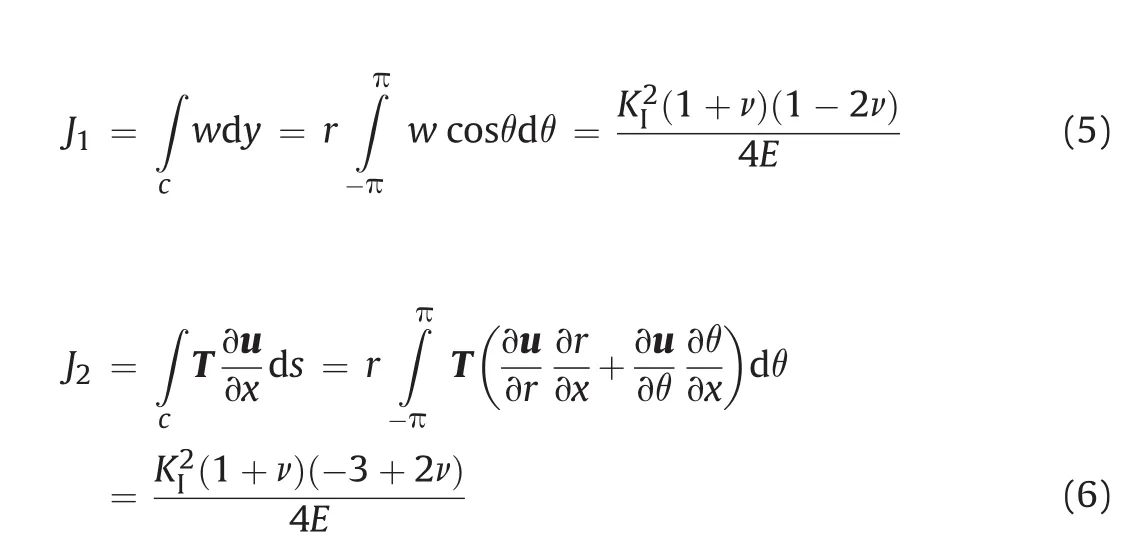
where c is the circular integration route.

The derivations of Eqs.(5)and(6)are presented in Appendix B.

2.1.Crack pressurized with fluid

For internally pressurized crack(as shown in Fig.2),the pathindependence of the J-integral around the crack tip is not applicable as the traction-free condition at the crack faces is not met.Therefore,an addition term is required to maintain this pathindependence.

Due to the traction force(hydraulic pressure)over the crack surfaces(see Fig.2a),the corresponding components of the J-integral on routesΓ2and Γ4are no longer zero and they can be expressed as follows:

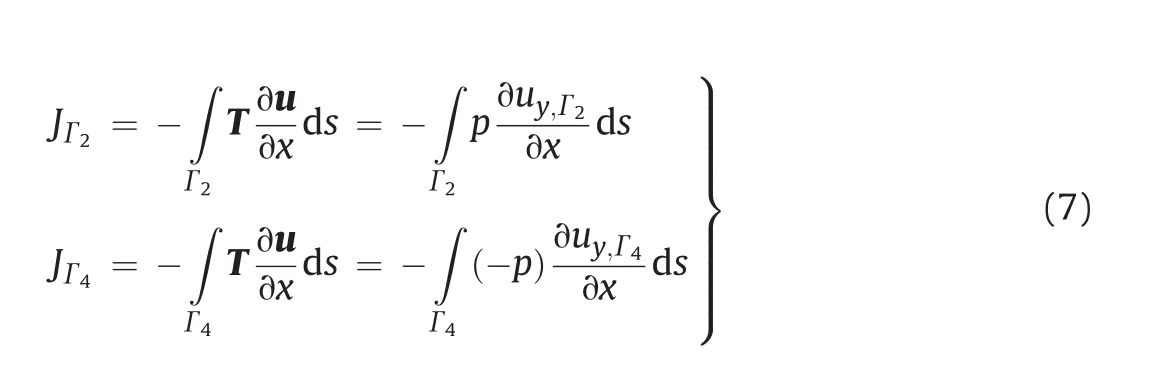
where p is the traction force(hydraulic pressure)over the crack surfaces.

Assuming that the crack is symmetric,and the end points of the route are also symmetric,it can be obtained that

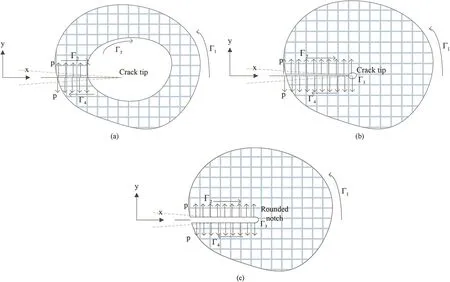
Fig.2.Cracks with hydraulically pressurized surfaces:(a)Sharp crack with enclosed annular area around the crack tip,(b)Sharp crack with inner path which is infinitely small around the crack tip,and(c)Inner path shrunk to a rounded notch.

AssumingΓ3to shrink to an infinitely small contour around the crack tip and yet excluding crack tip singularity(as shown in Fig.2b),or become a rounded notch(as shown in Fig.2c),the J-integral overΓ3can be expressed as follows(for enclosed path integral conservation,refer to Appendix A):

Since the pathΓ3is in clockwise direction(as shown in Fig.2b and c),J value in the opposite directionΓ3*is reversed,i.e.

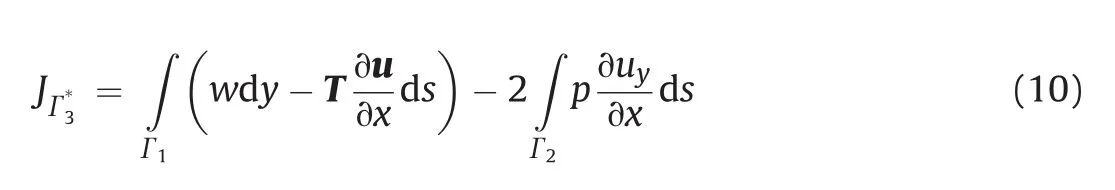
The length of pathΓ2in Eq.(10)can be approximated as the distance from the J-contour/crack face intersection to the crack tip.The extended J-integral is then presented as

where J is the original value along the path,andδrepresents the crack opening width(aperture).In fluid-driven cracks,before the cracks reach propagation criteria, fluid pressure builds up inside the cracks without flowing,therefore,the hydraulic traction force p is the same along the crack surfaces.With application of integration by parts,Eq.(11)can be written as follows:

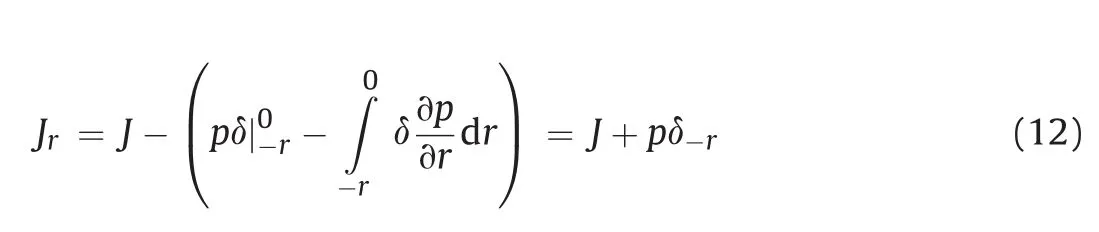
This extended J-integral is used to characterize local strain energy in case of hydro-traction crack faces.Eq.(12)is applicable when the start and end points are symmetric.For deviating end points,however,one readily obtains

where uy,1and uy,2denote the y-displacements of upper and lower end points,respectively.In this study,for the sake of simplicity,it is assumed that all contour edge points are symmetrically distributed on both crack faces,unless otherwise mentioned.

The extended J value can also be derived from an energy point of view.In case of the blunt fracture tip,J-integral can be shrunk to the flat surfaced notch and therefore,it can be used as a parameter to characterize the local strain energy.From the energy point of view,it can be deemed as the potential energy release rate.The potential energy of the area around the crack tip is

The first term at the right-hand side of Eq.(14)is the free energy of the body,while the second term is the energy coming from boundary loading.The body and the load together are treated as a composite system.If the crack propagates by a small amount da,the potential energy release rate is expressed as follows in terms of field variables:

whereσis the stress,and a is the distance that the crack propagates.

According to Rice(1968b),J-integral is equal to the energy release rate and can be expressed as

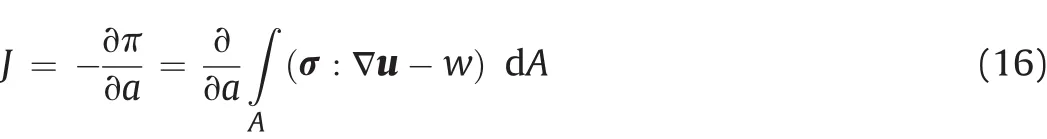
In case of internally pressurized cracks,the termdl in Eq.(14)includes the pressure workTherefore,the extended J-integral is also equal to the potential energy release rate of pressurized crack:

Since the energy interpretation of extended J-integral remains the same,and the domain integral method(Nikishkov and Atluri,1987),commonly used for calculation of J,is essentially based on the energy release rate,the domain integral method can,therefore,still be used in hydraulically pressurized fractures.In the following section,the extended J-integral for hydraulically pressurized crack surfaces is generalized to 3D conditions.

2.2.Point-wise 3D extended J-integral

J-integral was initially proposed for 2D problems.It becomes surface integral if a crack is in 3D,which can be derived in the same manner because of volume integral conservatory as

where s represents the wrapping surface around the crack front segment,and nxis the x-component of the unit vector normal to the wrapping surface.A schematic representation of cylindrical wrapping surfaces around cracks with constant and changing heights is shown in Fig.3a and b,respectively.Wrapping surfaces around the crack can be arbitrarily shaped,yet the surface geometry shown in Fig.3 is simplified as a cylinder for better understanding.In case of traction-free crack surfaces,J value is obtained by integration over side surface(B)as well as over top and bottom surfaces(A and C),respectively.In case of internally pressurized cracks,another term,which represents the effect of the loaded crack surfaces M and N(see Fig.3a and b),needs to be added to Eq.(18)as follows:

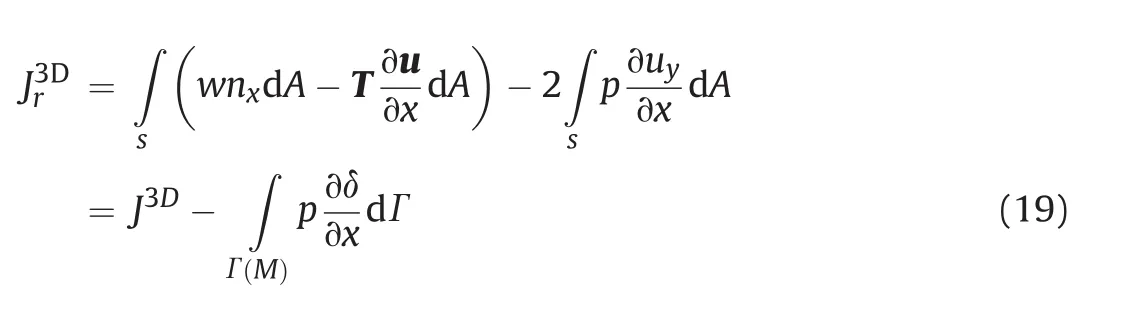
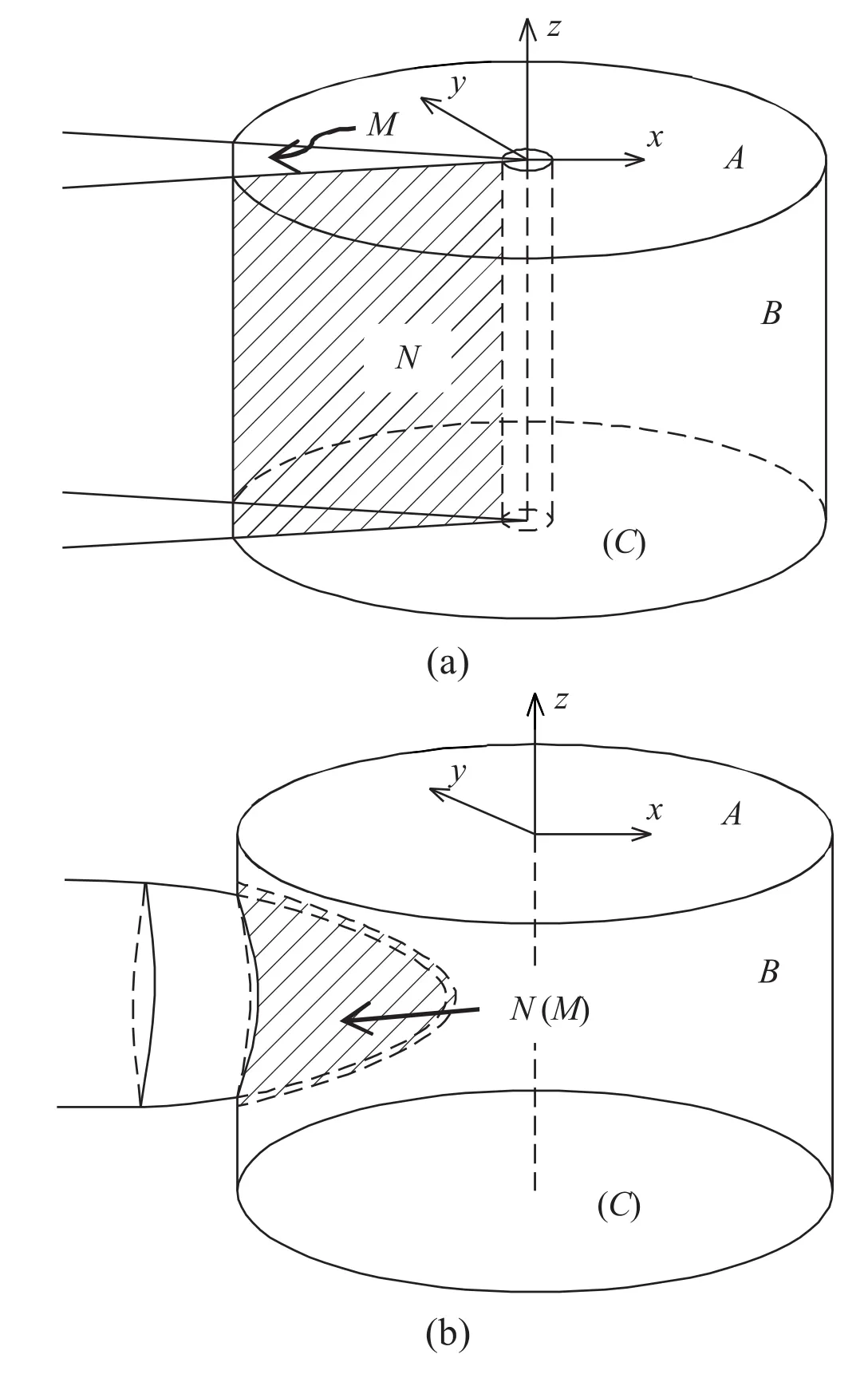
Fig.3.3D cracks and their wrapping surfaces:(a)Crack with constant height,and(b)Crack with changing height.

The surface integral in Eq.(19),J3D,a global parameter for 3D cracks,represents the accumulation of strain energy along the crack front,and can be expressed as follows:

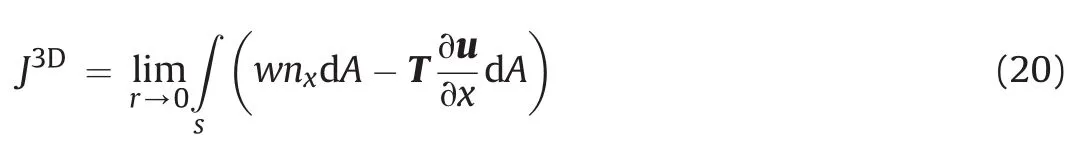
Numerical implementation of the 3D J-integral is,however,associated with the difficulties due to the presence of singularities.For instance,integration over the top and bottom parts of the wrapping surface in Fig.3a and the side cylindrical surface in Fig.3b needs displacement gradient to be calculated near the vertex singularity.Therefore,the numerical solution of 3D J-integral is relatively inaccurate and unstable.However,this is not the case with point-wise 3D J-integral.

For a specific point on the crack front,point-wise J-integral is defined to characterize the state of a point,as shown in Fig.4a.The point-wise J-integral can be calculated as follows(Nikishkov and Atluri,1987):

Fig.4.3D point-wise J-integral:(a)Infinitely small disk around a point at crack front(excluding singularity),and(b)3D point-wise J-integral on a plane normal to the crack front.

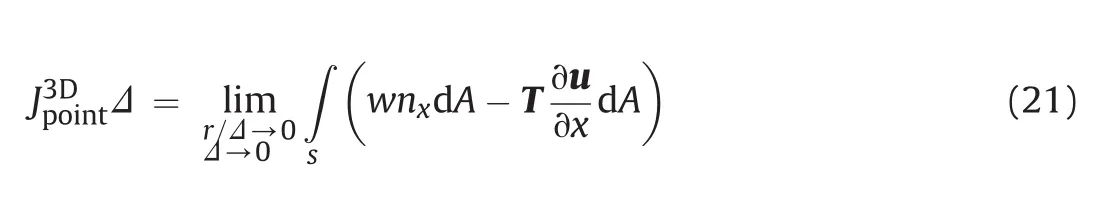
whereΔis the disk thickness,and r is the radius of the disk.Due to the conservation of the volume integral,and the application of the divergence theorem,the point-wise J-integral can be represented as

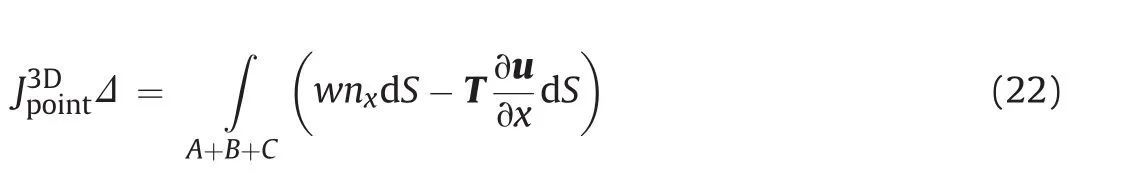
Since the normal vectors of faces A and C(top and bottom parts of the wrapping surface,as shown in Fig.4a)have opposite directions,the point-wise J-integral can be expressed as

where nxis zero in areas A and C.

Eq.(23)can be further simplified as

The pathΓresides on a plane,of which the normal vector is tangent to the crack front,as shown in Fig.4b.

Taking into account the hydraulic pressure,Eq.(22)is written as follows:

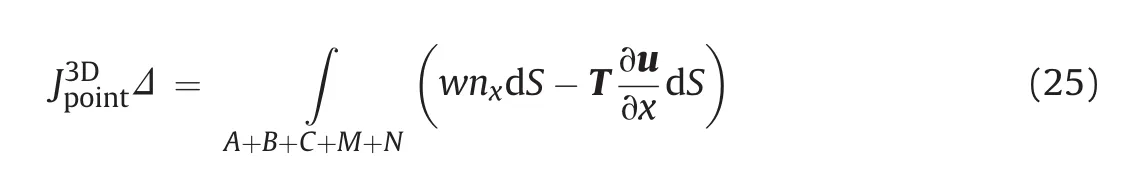
which can further be deduced to

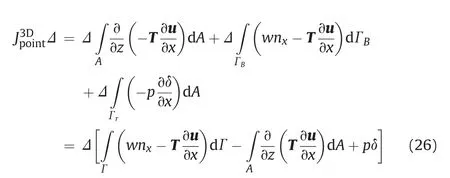
Therefore,the extended point-wise J-integral for 3D hydraulically pressurized cracks can be expressed as

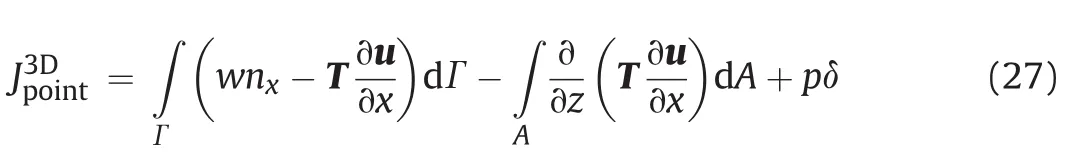
The line integral term and pressure term can be calculated away from the crack front,yet the area integral term is still related to area near the crack front.From the second term on the right side of Eq.(27),it can be noted that taking the gradient over z-direction eliminates strain singularity,which makes the numerical calculation of the point-wise J-integral more stable.This local value of point-wise J-integral indicates the stress state of a point at the crack front,and it changes along the crack front.

In the following part,we will explain that the point-wise 3D extended J-integral is also the energy release rate at that point along a fluid-driven crack front.We take out a volume around a crack line with constant thicknessΔ,as shown in Fig.5a.The potential energy of the crack tip front volume is

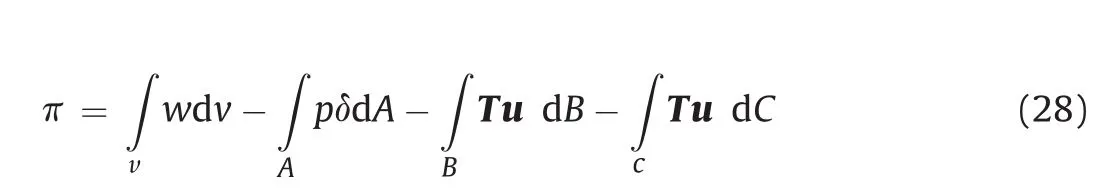
where A,B and C are shown in Fig.5.If the crack advances by an infinite small are aδA,the change of potential energy is π(A+δA)- π(A).If we transform Fig.5a so that the crack front

coincides with that in Fig.5b,the difference volume represents the difference in elastic energy,which is shown in Fig.5c.The difference volume can be acquired by considering a sweeping motion between Fig.5a and b.Therefore,we obtain the difference in elastic energy,i.e.∫Γ［-wnx（δA）］dΓ.Work done by the external traction also changes during sweeping.As to the work done by the traction on the circumferential area,the contributing difference isFor the top surface,consequently,the difference

in the work done by the traction iswhere δa is the increased crack length,δa= δA/Δ.Similar expression can be derived for the bottom surface.Finally,the contribution of the internal pressure to the potential energy difference is

With all the contributions described above,the energy release rate is

where C′is the bottom surface.

If the thickness is infinite small,the summation of integrals for the top and bottom surfaces can be expressed assince the tractions are in opposite directions.Therefore,the energy release rate can be further simplified as

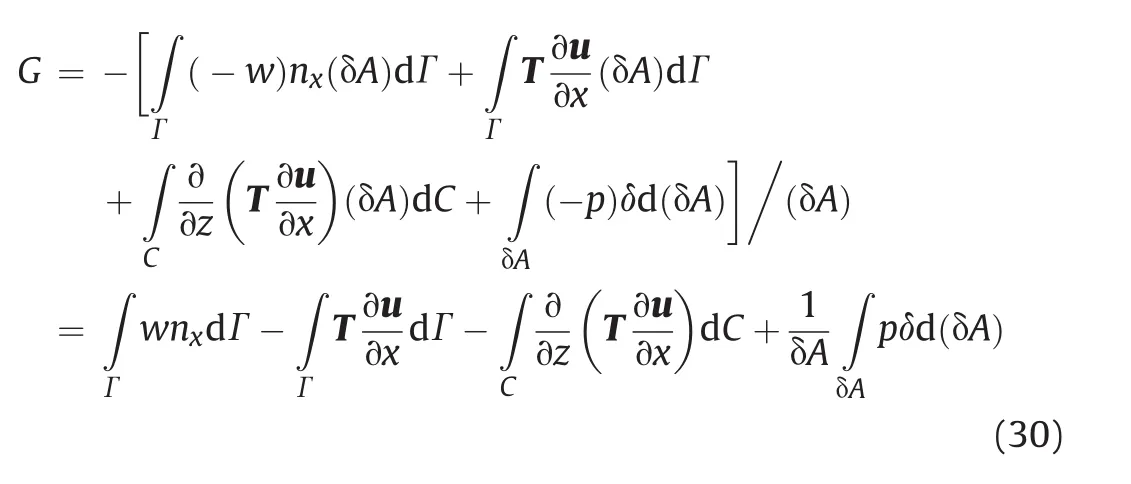
Eq.(30)is in accordance with the extended 3D point-wise J-integral.If we assume constant pressure and infinitely smallδA,the formula would be exactly the same with the extended 3D pointwise J-integral.It indicates that the energy release rate is naturally a point-wise characterizing parameter,and the extended 3D point-wise J-integral can be used to calculate the energy release rate in fluid-driven cracks.

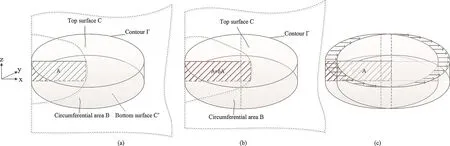
Fig.5.Near crack domain/volume:(a)Initial crack front domain,(b)Advanced crack front domain,and(c)Transformation of initial geometry to the advanced one so that the crack front coincides.

2.3.Extended J-integral for porous media

Petroleum reservoir rocks are porous media,hence the theory of poroelasticity applies.The concept of effective stressis usually adopted to describe the behavior of solid matrix,and is in constitutive relation with the strain,i.e.=Dε,where D is the stiffness tensor.Total stress at a point is the overall stress state based on the assumption that solid and fluid are overlapping.The numerical value of the total stress consists of the effective stress of solid skeleton and the fluid pressure.

In calculation of extended J-integral for porous media,it should be noted that the total stress instead of the effective stress should be used because the total stress is divergence free.Meanwhile,the definition of strain energy density can be expressed as

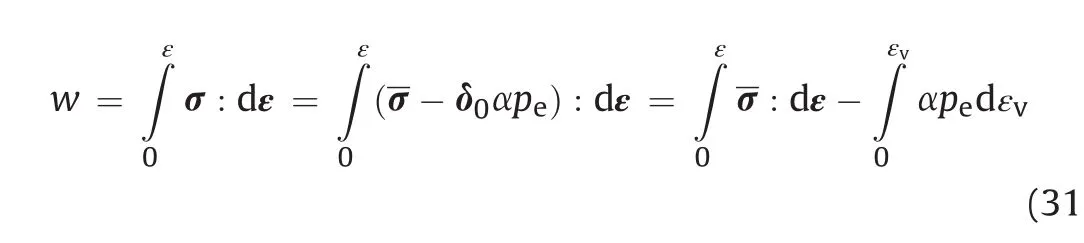
where peis the pore pressure in porous media,αis the Biot-Willis coefficient,εvis the volumetric strain,and δ0is the unit tensor.If wedefine a new strain energy density asw=:dε,we have

The extended 3D point-wise J-integral then becomes

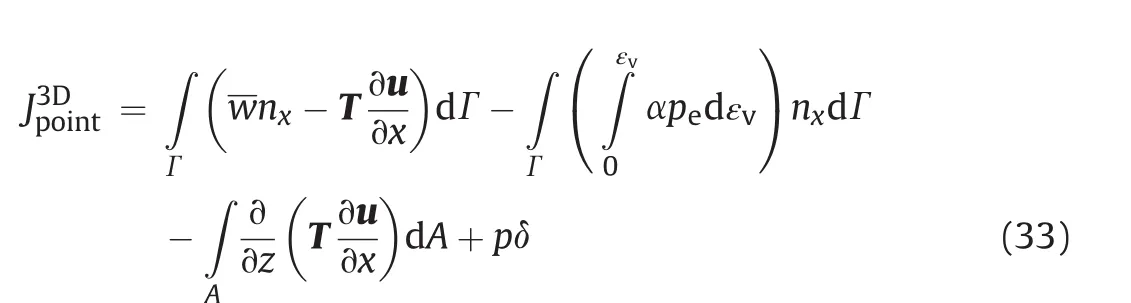
2.4.Effect of thermal stress/strain

During hydraulic fracturing,heat transfers between rock formation and fluid.In case of low-temperature fracturing,for example,the cooling liquid brings an intensive thermal strain along fracture surface,therefore,a coupling thermal field cannot be neglected in modeling.The acquisition method of J-integral should also be revised accordingly to retain its pathindependence.

Recalling Section 2.1,the path-dependence of the derivation of J relies on divergence free stress and small-strain assumption,therefore,in the definition of strain energy densitydε,stress is the mechanical stress while ε is the total strain.With thermal effects considered,the overall strain becomes

where εMis the mechanical strain,and εTis the thermal strain.The mechanical stress is then expressed as

where T0is the temperature compared to a reference value,andαTis the thermal expansion coefficient.Therefore,the strain energy density becomes

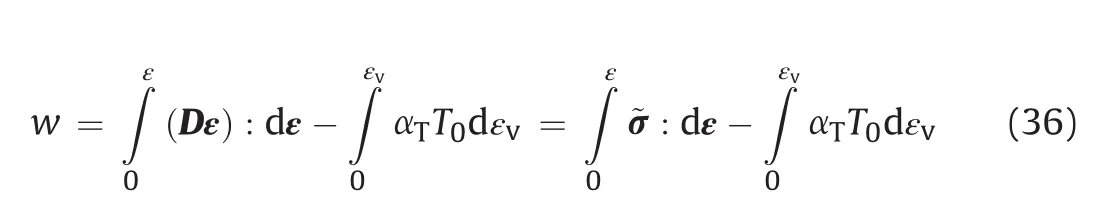
where~σis the stress calculated from total strain by~σ=Dε.If we define a thermal strain energy density~w=∫ε0~σ:dε,we have

The extended 3D point-wise J-integral then becomes

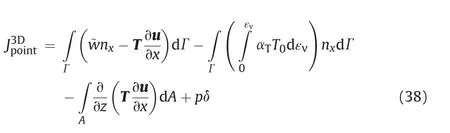
3.Numerical verification of path-independence of extended J-integral

The application of the extended J-integral is investigated using a case study in which a finite sized crack(see Fig.6)is located in a finite plate(representing the rock body in the planestrain condition).J value was obtained and processed through a numerically determined stress field after analysis.Only mode-I loading is considered in this study as it is the case in most hydraulic fracturing operations in which the fracture propagation occurs due to the tensile failure of the rock.The length and width of the rock stratum are 20 m and 8 m,respectively.The crack length is 3 m.

Bi-axial compressions,σxand σy,which are equal to 30 MPa and 20 MPa along x-and y-directions,respectively,are also applied as stress boundary conditions to represent underground in situ stress conditions.The Young’s modulus is set to be 20 GPa,and the Poisson’s ratio is 0.25.

Next,the proposed extended J-integral value is evaluated using the FEM.Five randomly chosen contours are used for integration,as shown in Fig.7.The hydraulic pressure p is increased monotonically from 23 MPa to 35 MPa.Table 1 shows the values of extended J and JEDI(J-integral calculated fromthe equivalent integral method)with different hydraulic pressures.It is shown that the extended J is path-independent,while the original J values change with the integration path.As the calculation of the original J neglects the surface traction,negative values are obtained,which have no physical meaning.The positive values of extended J indicate that energy is consumed when crack grows,usually in the form of surface energy and viscous dissipation.The relative error between different paths at a certain hydraulic pressure is less than 4%.The value of the extended J is consistent with JEDI,which satisfies its physical meaning as the energy release rate.As a crack tip condition indicator,the extended J value also increases when the hydraulic pressure increases.

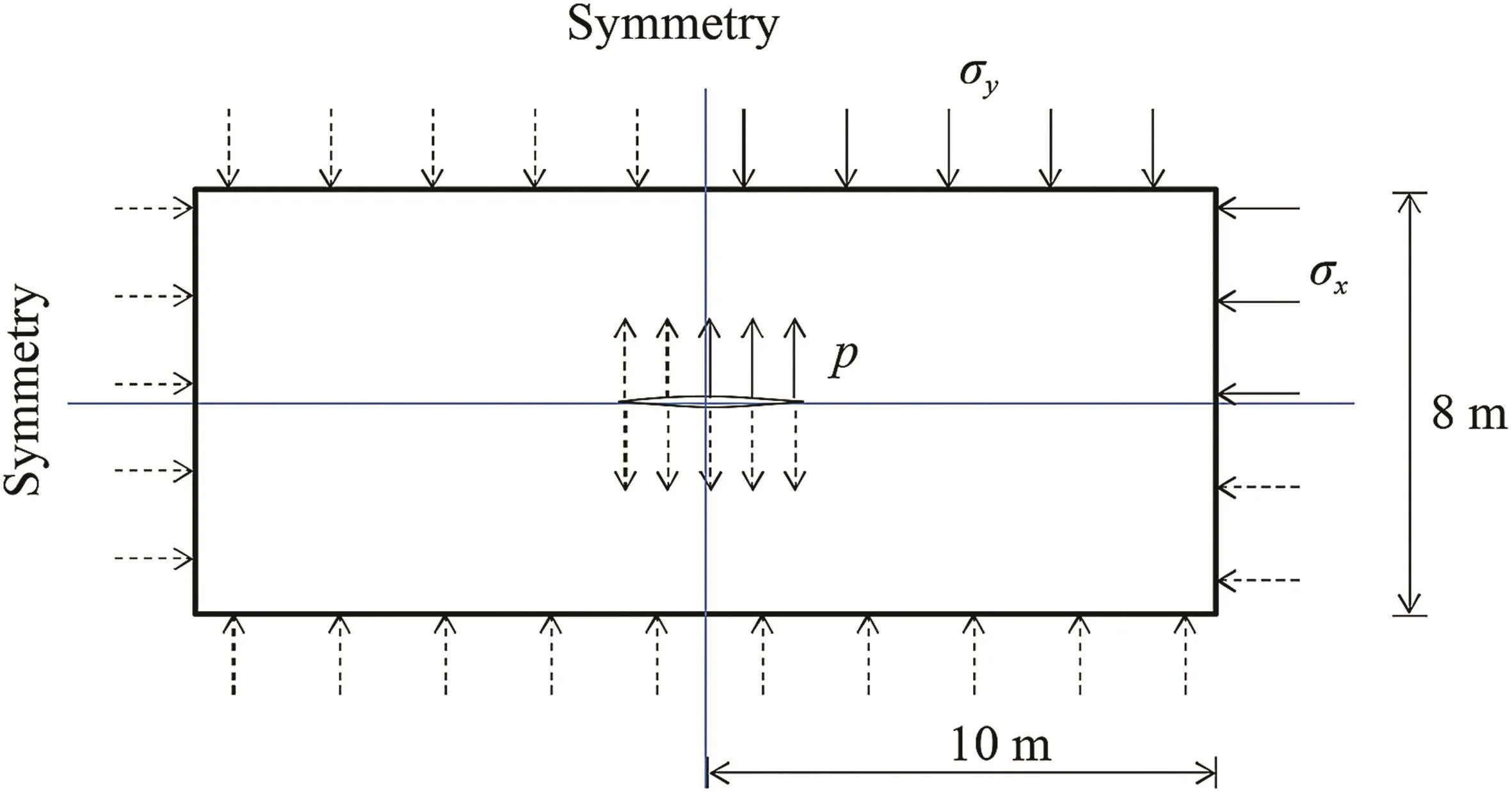
Fig.6.Mode-I hydraulically pressurized crack.

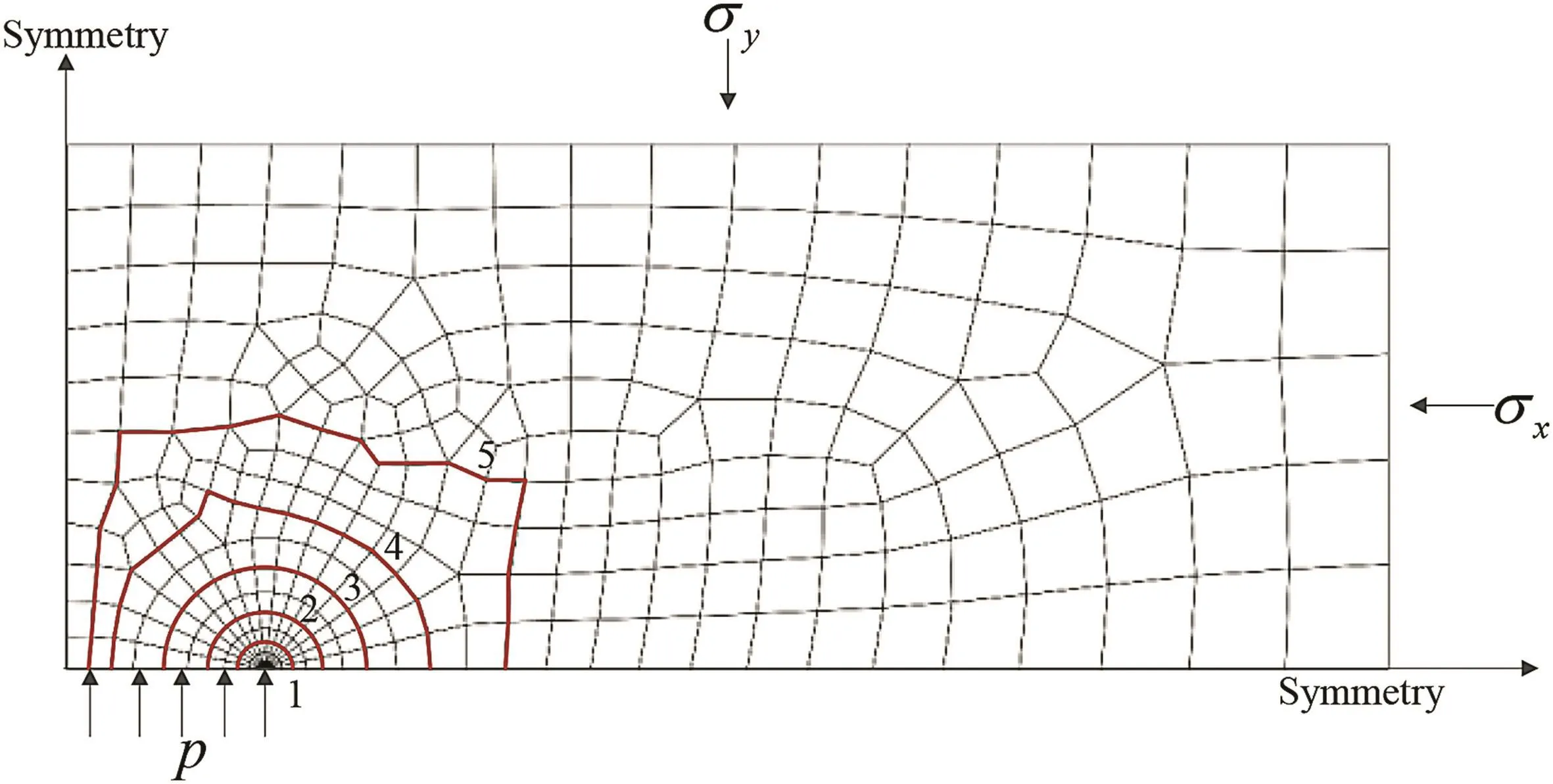
Fig.7.J-integral contours around crack tip in a quarter of model due to symmetry(the numerical values of individual contour are presented in Table 1).

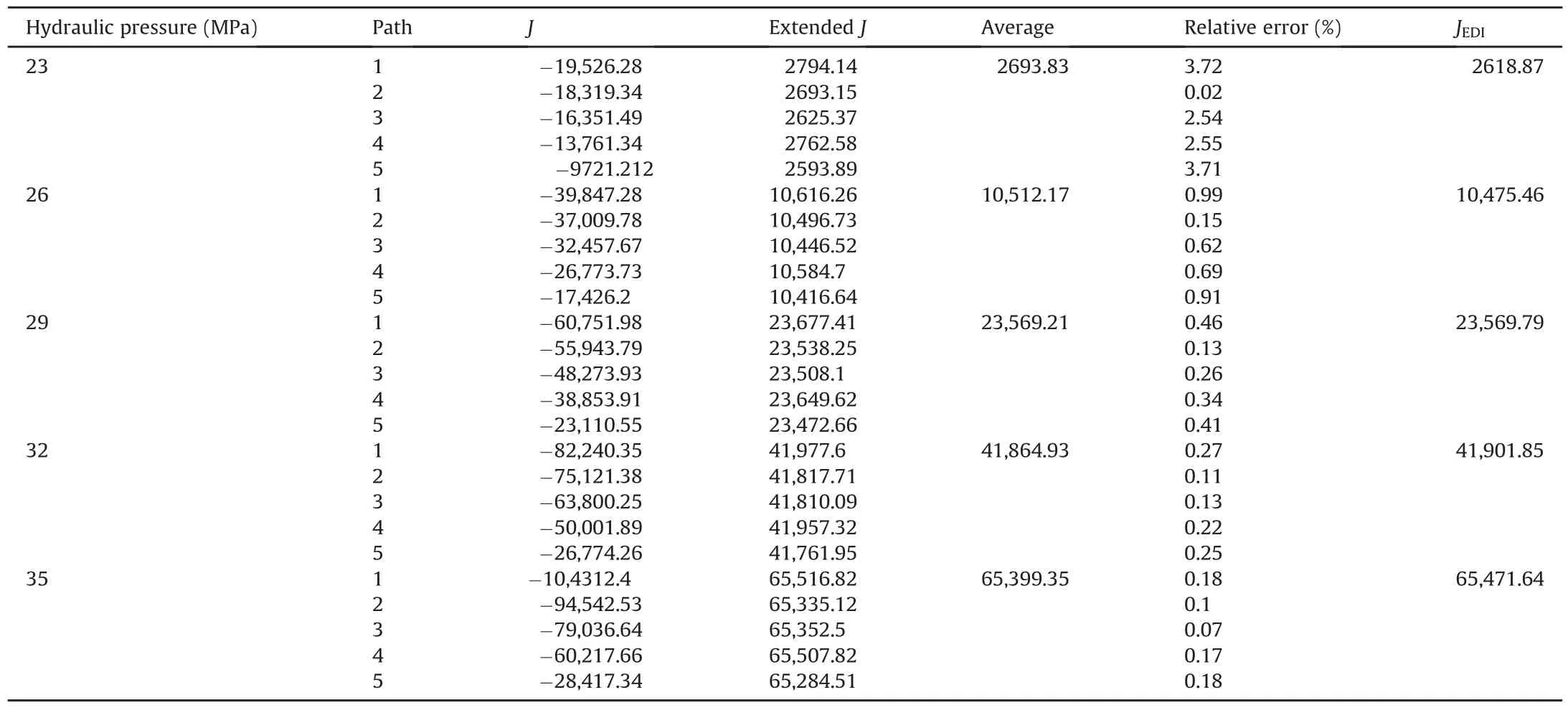
Table 1FEM analysis of hydraulic crack:Calculation of J-integral.

Table 2Comparison of extended J-integral values at elastic and elastoplastic conditions.

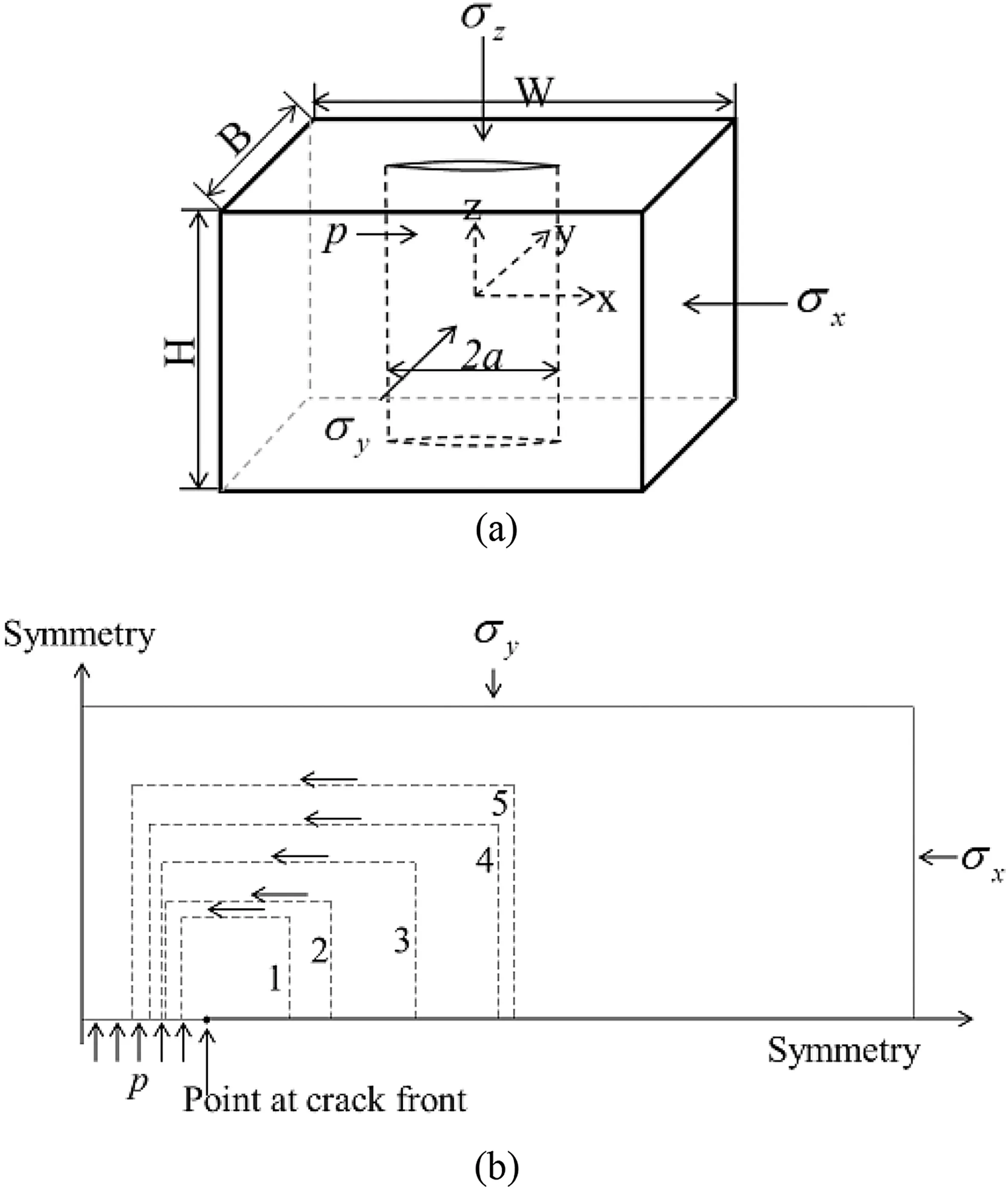
Fig.8.(a)3D hydraulically pressurized crack,and(b)A quarter of the plane normal to crack front at z=0.4 m with 5 paths around the crack tip.

If we analyze the crack using incremental plasticity(yield stress is 50 MPa with perfect plasticity),the J-integral value is also obtained as path-independent.The value is compared with that in elastic condition at hydraulic pressure of 35 MPa,as shown in Table 2.

For the 3D extended point-wise J-integral,numerical computation involves area integral,line integral,and the third term whichis related to hydraulic pressure.Equivalent domain method is also implemented for comparison(a detailed derivation of EDI is shown in Appendix C).The 3D model and integral routes/areas are represented in Fig.8.Five rectangular paths are chosen at the plane normal to the crack front at z=0.4 m for simplicity(the range of z is from-4 m to 4 m).The parameters used in the simulation are presented in Table 3.

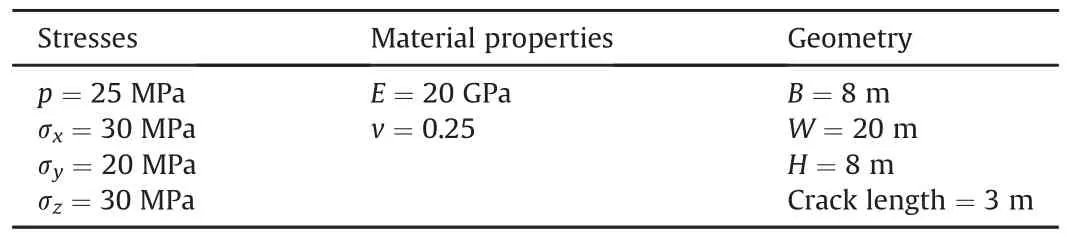
Table 3Parameters used in numerical calculation.

Table 4FEM analysis of 3D point-wise extended J-integral.

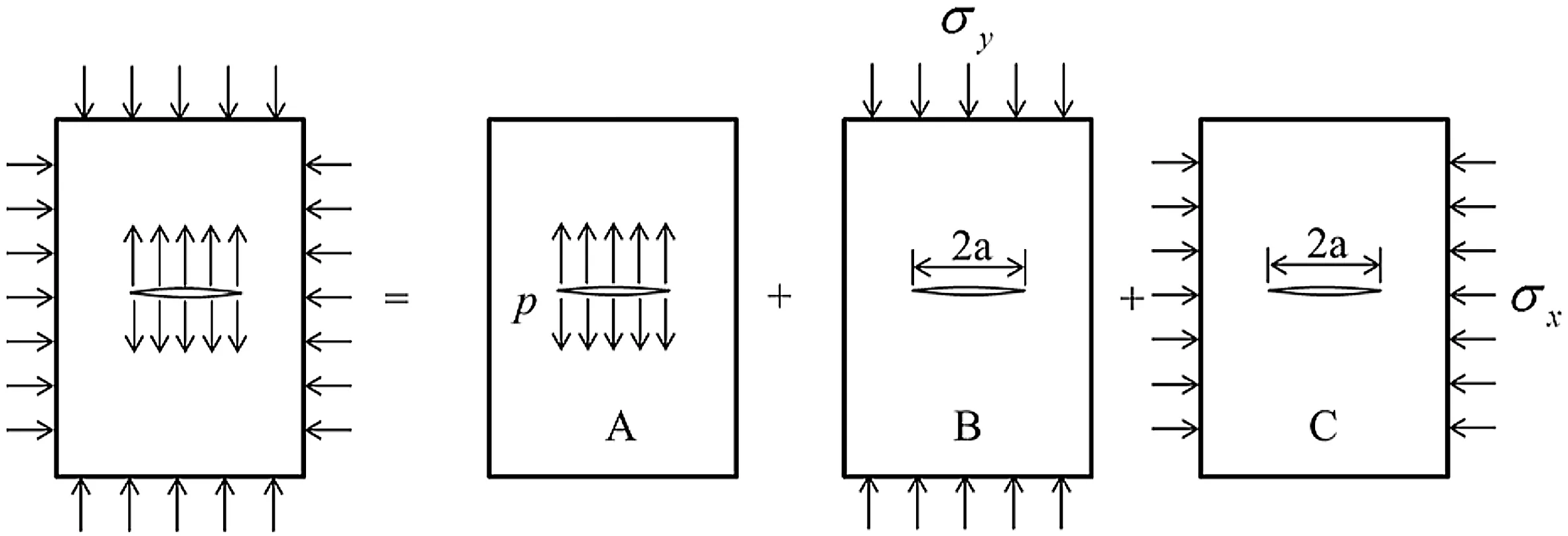
Fig.9.Underground pressurized crack.

The numerical results of 3D J-integral calculation are presented in Table 4.The line integral term in each path,which is the exact expression of original 2D J-integral,is not pathindependent.The extended 3D J-integral is verified to be constant in different integration paths with a relative error of less than 1.5%.It is also consistent with JEDI,which indicates that the extended 3D J-integral is equal to the energy release rate as well.This value also represents the energy intensity of crack front at z=0.4 m.

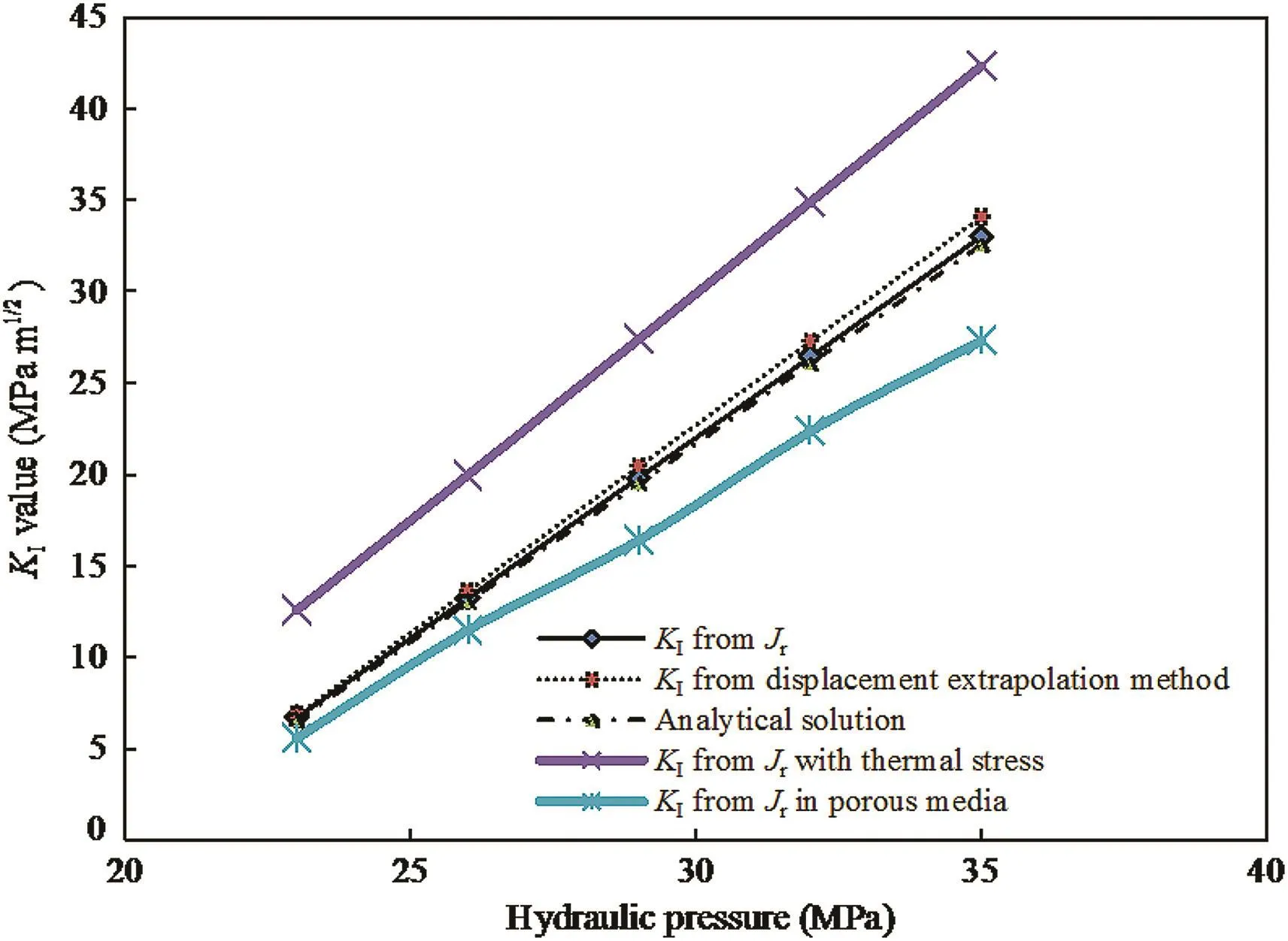
Fig.10.Stress intensity factors calculated from the revised J-integral at different hydraulic pressures.

Because the revised J-integral is another form of energy release rate,it allows us to calculate SIF and compare it with that obtained by the conventional displacement extrapolation method.The theoretical equation of SIF for the geometry in Fig.6 can be derived by superposition principle(Broek,1982)based on which the internally pressurized crack under far- field x-and y-stress boundary conditions can be presented as the superposition of(i)a plate with an internally pressurized crack(case A),(ii)a plate with a crack under uniaxial compression in y-direction(case B),and(iii)a plate with a crack under uniaxial compression in x-direction(case C),as shown in Fig.9.The corresponding SIFs can then be expressed as

The general solutions for cases A,B and C were readily obtained by Irwin(1957)using the method of Westergaard(1939)as follows:

Therefore,according to Eq.(39),the total SIF in the mode-I loading for a finite sized and internally pressurized crack in an infinite plate under far- field stress boundary conditions can be expressed as

For the above-mentioned 2D plane-strain model,Eq.(2)is used to calculate the SIF with J substituted by the revised J.As shown in Fig.10,the estimated SIF is consistent with the analytical solution and that obtained from the displacement extrapolation method.It is therefore concluded that the relationship between the revised J-integral and the SIF remains valid.The partial discrepancy arises from finite dimension model and finite mesh.Separate curves are also shown for the cases of thermal stress(with a temperature drop of 50°C at the crack surface)and porous media,respectively.The corresponding results are in agreement with the general opinion that the SIF is increased by the thermal shock,while it is impeded due to diffusion in porous material.

4.Conclusions

J-integral has been extended for its application to fluid driven fractures and thus it can be employed in the field of hydraulic fracturing.The capability of the proposed 3D extended J-integral to calculate the energy release rate was successfully retained.A detailed formulation of the extended J-integral was presented.

The extension of J-integral is associated with internal traction.For 2D hydraulic fractures,the extended J-integral has an extra pressure term,which accounts for the effect of hydraulic pressure.Its path-independence has been numerically investigated successfully.For 3D hydraulic fractures,there are two forms of extended J-integral,one is the surface integral which represents overall strain energy accumulation along the crack front,and the other is the point-wise extended J-integral which accounts for the state of a point at the crack front and is decomposed into three parts(a line integral,an area integral and a pressure term).The calculation of the area integral term in the point-wise extended J-integral requires near-tip field data.It can be acquired numerically with high accuracy and stability due to the partial derivation in z-direction that eliminates singular term.Its path-area independence is also well examined.Besides,the 3D extended J-integral has also been discussed for porous media and under thermal conditions;an extra term is added to the formula respectively to re-establish its path-independence in such cases.In addition,two distance-independent circular integrals in K-dominance zone are found,which can be used to calculate SIF,an alternative to the conventional approach.The proposed methodology allows us to successfully utilize the path-independent integral(J-integral)in the hydraulic fracturing applications,especially under elastoplastic conditions,such as in coal seam and shale gas reservoirs.

Conflicts of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

List of symbols

E Young’s modulus

KIMode-I stress intensity factor

n Unit vector normal to the path

p Fluid pressure applied on crack surface

T Traction along the path

u Displacement vector

ux,uyx-and y-components of displacement vector

w Strain energy density

σ Stress tensor

ν Poisson’s ratio

ε Strain tensor

δ Crack opening width

Appendix A.Supplementary data

Supplementary data related to this article can be found at https://doi.org/10.1016/j.jrmge.2018.04.009.