平原丘陵过渡区土壤有机质空间变异及其影响因素

杜佩颖 张海涛 郭 龙 杨顺华 章 清 田 雪

（华中农业大学资源与环境学院，武汉 430070）

土壤是在成土因素的长期相互作用下形成的复杂自然综合体，具有高度的空间异质性和依赖性。土壤有机质（Soil Organic Matter, SOM）是土壤肥力的主要来源，对农业生产和可持续发展具有重要意义，因此了解土壤有机质的空间分布，掌握其空间变异规律对生产实践具有重要的指导意义［1-3］。

目前地统计模型已经被成熟地应用于土壤有机质空间变异规律的研究中，以变异函数为工具的区域化变量理论得到了广泛应用［4-5］。普通克里格方法（Ordinary Kriging, OK）作为经典的地统计模型较好地考虑了土壤样点属性的空间异质性和依赖性，但OK未将环境影响因子纳入模型，忽视了土壤属性在形成、发育和迁移过程中会受到的多种自然社会因素的影响。因此在构建土壤属性模型时考虑不同环境因素对土壤有机质空间变异规律的影响具有重要意义，为建立精确的土壤属性空间模型提供有价值的辅助信息［6-7］。

众多研究表明土壤有机质受到气候、植被、地形、土壤营养元素、土壤质地、土壤pH以及人为活动等因素的综合影响［8-10］。因此为进一步准确描述土壤有机质及其影响因素之间的响应机制，学者们将土壤有机质的异质性及其环境影响因素纳入模型，进行了土壤有机质预测和制图等方面的研究：例如，连纲等［7］以黄土丘陵沟壑区县域土壤有机质为研究对象，利用多元线性回归模型进行空间预测，结果表明包含地形湿度指数、高程、林地、梯田和土壤调节植被指数的区域回归模型具有最优的预测效果；郭月峰等［11］利用老哈河流域的地形因子对土壤有机碳建立多元线性回归模型，结果表明高程和坡度对该区域土壤有机碳影响作用较强。这些研究结果不仅进一步表明了环境变量与土壤有机质之间的密切联系，更为进一步进行土壤有机质预测及制图提供了发展方向及理论基础。

多元线性回归模型将整个研究区域当作一个研究整体，未考虑回归系数的空间局部差异，因此线性回归模型虽然可以揭示土壤有机质与环境变量之间的关系，但是难以建立土壤有机质与环境变量关系在局部区域上的差异性［12-13］。地理加权回归（Geography Weighting Regression，GWR）模型作为局部线性回归模型，不仅考虑了土壤属性的空间异质性，同时考虑了环境变量与土壤属性之间的相关关系的空间非平稳性［14-16］。GWR模型可以根据土壤属性的空间变异规律调节并选择合适的带宽，反映环境影响因子对局部地理位置土壤有机质的影响程度。GWR模型目前较多地被应用于土壤属性的预测和模拟中，但是由于GWR模型的前提假设是纳入模型的变量和残差具有独立性，因此土壤有机质和环境变量在空间上的依赖性会违背GWR模型的前提假设，并且影响模型性能的可靠性，为此GWRK模型由于其考虑了回归残差自相关性的独特优势被广泛地应用于土壤学领域［24, 26］。

本研究区内土壤有机质影响因子复杂，土壤有机质在局部区域表现出很强的异质性，因此利用传统的地统计模型难以准确模拟土壤有机质的空间局部特征，而多元线性回归模型无法考虑环境变量与土壤有机质的空间异质性［21］。为此本文选取GWR模型作为基础研究模型，探讨影响因子对土壤有机质局部区域影响作用的差异性，同时利用GWRK模型将GWR模型的预测结果与OK进一步结合，以达到更好的预测精度和效果。杨顺华等［20］曾以此区域为研究对象，将地形因子纳入回归模型对土壤有机质含量进行了预测，并得到GWRK具有较高预测精度的结论，但是该研究没有进一步探讨土壤有机质与自身物理化学性质之间的关系，为此本文进一步完善辅助数据集，为过渡地带复杂环境下数字土壤制图提供研究基础，同时该研究也未进行土壤有机质影响因子空间非平稳性影响的研究，本文通过影响因子系数分布图深入分析了各影响因子在局部区域对土壤有机质影响作用的变化规律。本文的主要研究内容为（1）建立由地形因子和土壤属性因子组成的土壤有机质预测辅助数据集，（2）运用GWRK预测土壤有机质含量并得到其空间变异规律，为平原丘陵过渡地带数字土壤制图提供参考依据，（3）分析土壤有机质影响因子变化规律，结合研究区地形特点和土壤有机质分布情况分析影响因子对土壤有机质影响作用的空间非平稳性。

1 材料与方法

1.1 研究区概况

本研究区位于宜都市枝城镇境内（图1）。宜都市位于3 0°0 5′～3 0°3 6′N，111°05′～111°36′E之间，地处湖北省西南部，江汉平原西部。枝城镇位于宜都市东北部，是江汉平原向鄂西山区的过渡地带，亚热带季风气候，四季分明，雨热同期，年平均降水量1 212 mm，气温16.7℃，无霜期273 d，地形地貌以平原、丘陵为主，地势西南高，东北低，大部地区属武陵山脉的丘陵地带，东北部临长江有部分冲积平原。结合地形地貌，在实地调查的基础上选取一块面积100 km2地形起伏较明显的代表性区域作为研究区，研究区最高点海拔为483 m，最低点为0 m，高程起伏变化较大，土壤类型主要有黄棕壤土类、石灰岩性土和水稻土类等，土地利用类型主要有林地、水田、旱地和园地，水田的种植方式为水稻轮作，一年两季，旱地多种植玉米、土豆等农作物，园地主要种植柑橘和茶树。

1.2 样品采集与分析

500个样点土壤样品采集于2013年12月—2014年1月，布点方法采用“网格+随机”相结合，遵循平原区域较稀、山区加密的原则，采样方法主要使用“梅花法”，对于较狭窄的地带或农田采用“蛇形法”。土样选取0～20 cm表层土壤，并使用差分式全球定位系统（DGPS）记录实地样点的空间位置。土壤有机质含量采用重铬酸钾氧化—外加热法测定，机械组成采用马尔文—激光粒度仪测定，使用美国制分级：砂粒（2～0.05 mm），粉粒（0.05～0.002 mm），黏粒（＜0.002 mm），土壤容重采用环刀法测定［22］。

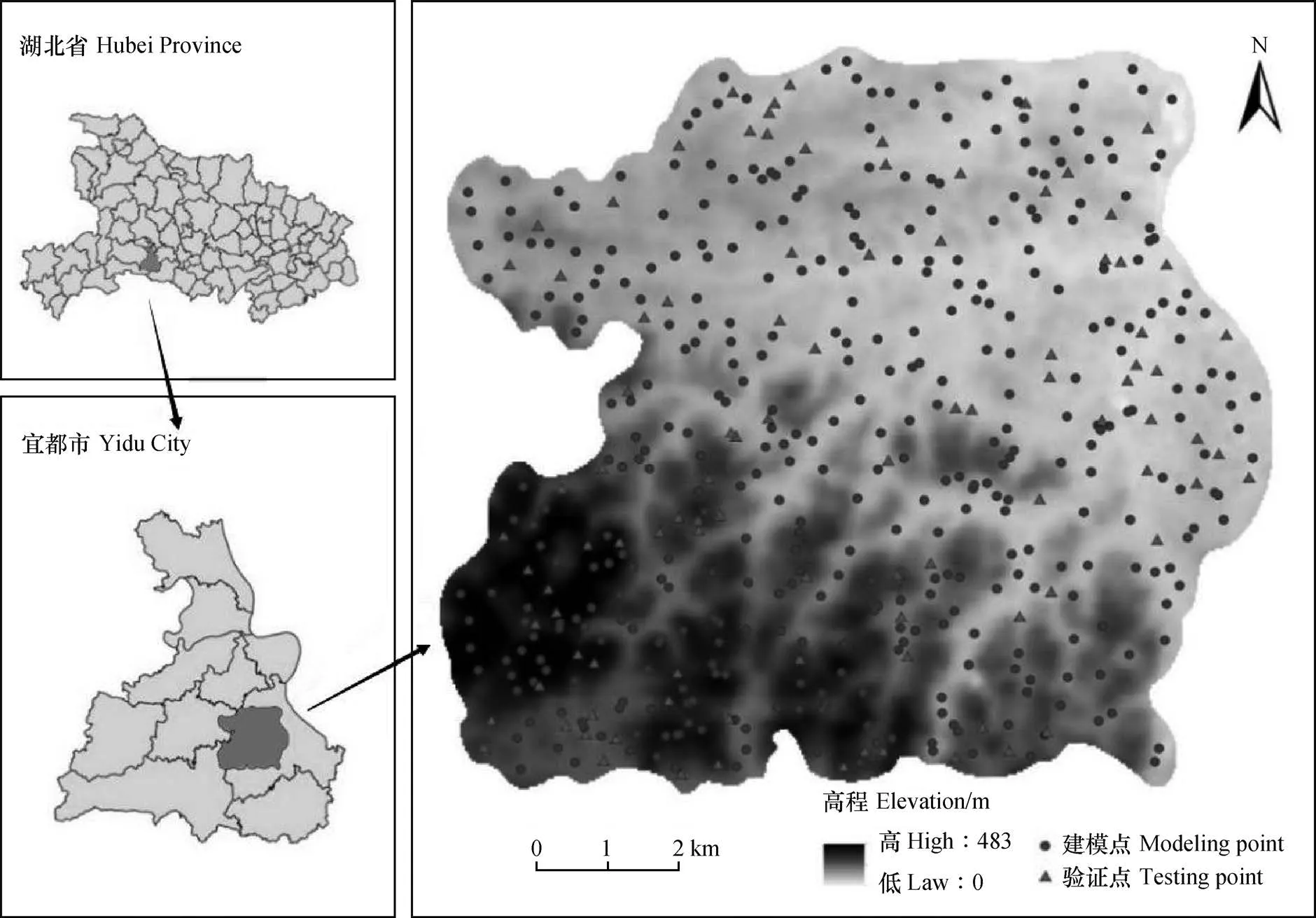
图1 研究区位置及采样点分布（392个建模点和98个验证点）Fig. 1 Location of the study area and distribution of sampling points (including 392 for modeling and 98 for validation in the study area

1.3 辅助信息获取

研究区的数字高程模型（D E M）数据（30 m×30 m）来源于国际科学数据共享平台（http:/ /datamirror.csdb.cn /admin /datademMain.jsp），利用DEM数据获取其衍生数据变量，主要为坡度（Slope）、坡向（Aspect）、高程（Elevation）、粗糙度（Roughness）、地形湿度指数（Topographic Wetness Index，TWI）、汇流动力指数（Stream Power Index，SPI）、沉积物运移指数（Sediment Transport Index，STI）。其中坡度采用ArcGIS10.2中空间分析模块中的相关工具直接提取，其余环境因子使用ArcGIS10.2中的栅格计算器以及水文分析模块综合计算获取。

1.4 提取影响土壤有机质含量的重要指标

除地形因子外，土壤属性因子也是影响土壤有机质含量的重要指标，因此除上文提到的地形因子外，加入有效铁(AI)、土壤pH、容重（BD）、砾石度（GD）、归一化植被指数（NDVI）、亚铁矿物指数（FMI）和土壤机械组成（包括黏粒、粉粒、砂粒）这7个属性作为辅助变量，组成由14个辅助因子组成的初选因子集，将土壤有机质含量与影响因子进行皮尔逊相关分析和逐步回归分析，筛选出与土壤有机质含量显著相关的影响因子。利用逐步回归方法选取进入模型的回归变量，既能保证与土壤有机质含量极显著相关的辅助因子进入回归模型，又能有效去除自变量之间的共线性，使用该方法得到研究区GWR模型的最佳解释变量：Elevation、Slope、Aspect、AI、BD、GD、Clay。

1.5 模型方法

（1）回归克里格（RK）方法［25-26］首先对解释变量和目标变量之间的回归关系进行探讨，建立两者之间的线性回归关系，进而由回归关系得到目标点处的确定性趋势项，对分离趋势项后的残差进行普通克里格（OK）插值得到残差项，最后将趋势项和残差项相加得到采样点处的RK预测值。

（2）地理加权回归克里格（GWRK）［12,19,27］是一种局部回归方法，它将全局回归方法中的全局回归值换成GWR局部回归值，同时考虑了局部预测的残差。GWRK是对GWR的延伸与扩展，即对局部模型GWR拟合后得到的残差进行OK插值，然后与GWR拟合的趋势相加。

（3）数据标准化。在评估解释变量对SOM的影响时，预测模型中的系数是一个可以定量比较的指标，但在进行这一过程之前，必须对解释变量进行标准化转换，将解释变量的量纲进行统一，标准化后的变量其系数越大说明它对土壤有机质的影响程度越高，标准化公式如下：

式中，χ*为标准化结果，χ 为解释变量的原始值，μ为变量的均值，σ为变量的标准差。

（4）模型精度验证。为综合比较模型的预测精度，从数值上精确比较预测效果，本文选择平均误差（ME）、平均绝对误差（MAE）、均方根误差（RMSE）、皮尔逊相关系数（Pearson’r）以及不精确度（IP）等指标评估预测精度。本研究利用箱线图法剔除异常值10个，利用ArcGIS中的工具将490个样点随机分为两组，其中一组392个（占样点总数的80%）作为建立模型的拟合数据集，另一组为其余98个（占样点总数的20%）作为验证数据集用于验证模型。

2 结 果

2.1 土壤有机质描述性统计特征

由表1可知，建模点的土壤有机质含量在3.80～69.40 g·kg-1之间，平均值为28.42 g·kg-1，变异系数为39.86%，属中等变异，土壤有机质含量不符合正态分布，经对数转换后通过K-S检验，符合正态分布。研究区高程均值为172.3 m，最小值为0 m，最大值为483 m，变异系数为65.06%，具有较强的变异程度，高程变化幅度较大；坡度和坡向的均值分别为9.31°和177.2，变异系数分别为80.02%、58.49%，变异系数较大，说明地形起伏程度较大；有效铁、土壤砾石度、黏粒的变异系数分别为93.89%、162.1%和51.10%，研究区土壤属性因子变异程度较大。

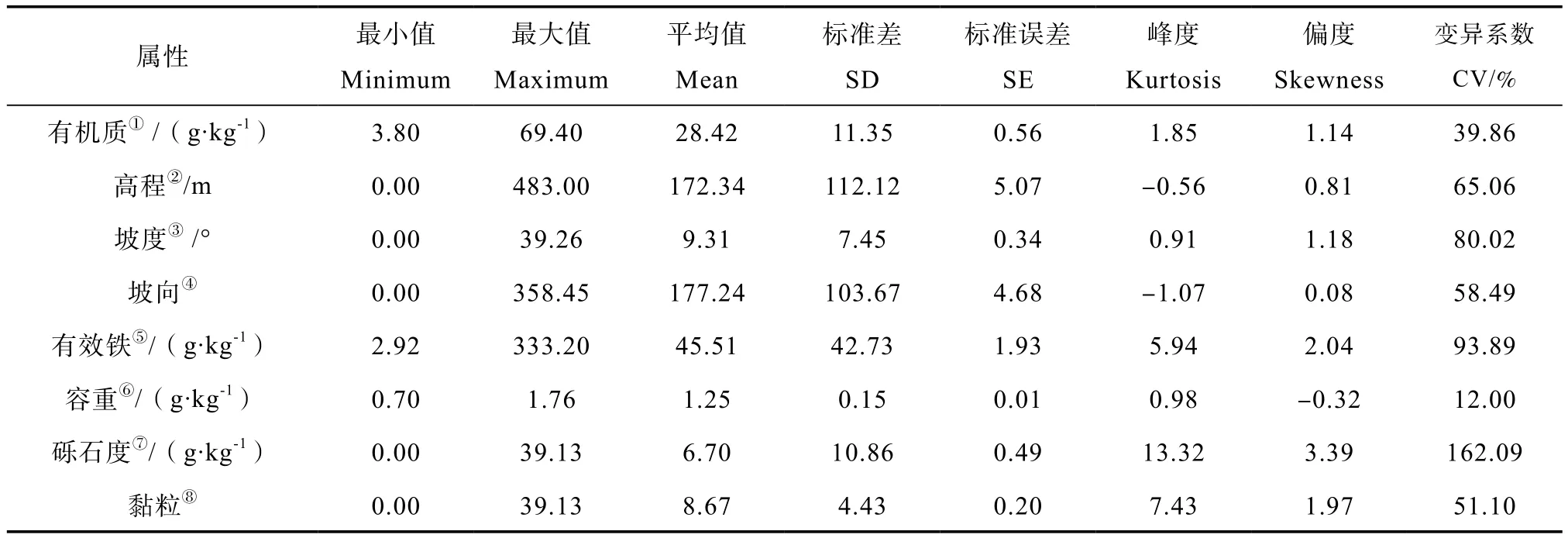
表1 土壤有机质含量及其影响因子的描述性统计结果Table 1 Descriptive statistic of soil organic matter (SOM) and its affecting factors

2.2 土壤有机质预测模型的建立

土壤有机质预测模型中使用高程、坡度、坡向、有效铁、容重、土壤砾石度和黏粒7个影响因素作为解释变量建立多元线性回归模型（MLR）和地理加权回归（GWR）。MLR模型参数的统计结果表明，高程、坡度和土壤容重系数的绝对值大于坡向、有效铁、土壤砾石度和黏粒含量，系数越大表明影响程度越大。土壤有机质含量与高程、坡度、坡向、有效铁和土壤砾石度呈正相关，而土壤有机质与土壤容重和黏粒呈负相关。方差膨胀因子（VIF）在逐步线性回归中反映了冗余的解释变量信息，VIF大于7.5的解释变量存在局部共线性需要去除，本模型中VIF均小于7.5，7个解释变量均适合纳入模型。

GWR是局部回归模型，解释变量的回归系数在研究区内随空间位置的不同随之变化， GWR模型参数的统计结果显示，解释变量的范围、最小值、最大值、平均值、标准差和变异系数如表所示。GWR模型中的参数与MLR有着类似的含义，系数范围、标准差和变异系数用来描述解释变量空间系数的分布情况，除土壤容重外，其他解释变量均具有强空间变异性（＞35%）。

2.3 土壤有机质预测模型

由表2可知，土壤有机质含量、线性回归残差和地理加权回归残差的理论半方差模型分别为指数模型、指数模型和球状模型。块金值分别为0.021、0.032、0.087，说明土壤有机质存在较小的随机性误差。块基比分别为0.23、0.19、0.16，说明三个模型存在不同程度的空间自相关性，且均小于25%，适合进行普通克里格插值。变程分别为142 3 m、134 3 m和158 0 m，在此范围内的空间变量具有空间自相关性，变程以外则不存在；三者的决定系数均在80%以上，取得了较好的模型拟合效果，较小的残差平方和也表明了拟合点和拟合曲线之间较好的吻合效果。

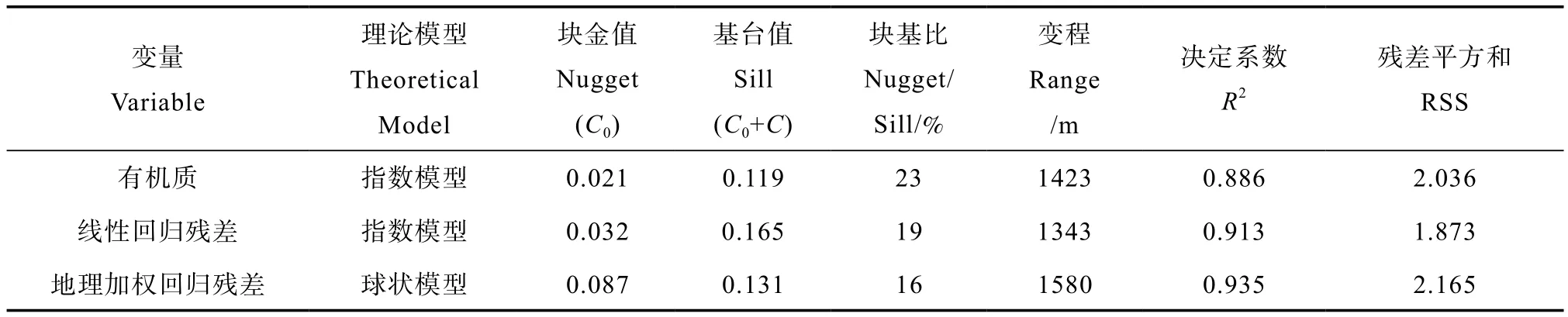
表2 有机质、线性回归残差和GWR残差的半方差函数模型及参数Table 2 Semi-variance models of SOM, OLS and the residuals of GWR and parameters involved

采用OK、RK和GWRK三种方法分别预测研究区土壤有机质含量（图2），从图中可以看出，GWRK预测得到的SOM区间范围较OK和RK更大；三种方法的预测结果在整体上趋势一致，高值区集中分布在研究区东北部，低值区聚集在南偏东方向，在研究区南部及西南部也有部分低值区域存在；GWRK在低值区域的预测范围更大，OK和RK在高值区域的预测范围更大，整体上呈现出“高低值区域缩小，中值区域扩大”的趋势；在高低值过渡的区域，OK和RK的过渡范围小，过渡幅度较大，存在过渡区突变的情况，过渡不够平缓，而GWRK在过渡方面则体现出更好的效果，过渡较为平缓，整体上没有较突兀的显示效果，高低值界线更加模糊化，过渡曲线更加曲折，这与实际SOM分布规律更加吻合。从空间分布图上来看，GWRK具有更好的预测效果，这主要是因为GWRK更好地考虑了局部影响因子对土壤有机质的影响作用，更加全面、准确地将解释变量纳入模型，同时考虑了预测残差，有利于反映研究区细节变化特征，使预测结果与真实值更加接近，有助于掌握SOM的整体分布情况。

2.4 预测模型精度评价

为进一步说明GWRK预测精度，引入模型评价指标对预测模型进行精度评价。选用平均误差（ME）、平均绝对误差(MAE)、均方根误差(RMSE)、不精确度（IP）和相关系数（r）五个指标进行模型评价。从表3可以看出，三者的ME均为正值，说明预测值整体水平较实测值偏低，GWRK平均误差最小；GWRK的MAE和RMSE均小于其他两者的结果，降低程度分别为26.76%和39.28%；不精确度则是OK、RK高于GWRK；GWRK的相关系数 r 高于OK和RK。由定量数据分析可知，局部预测模型GWRK较OK和全局模型RK预测精度更高。

2.5 影响因子的空间非平稳性分析

为说明解释变量对SOM影响作用的变化规律，绘制解释变量系数空间分布图，如图3。

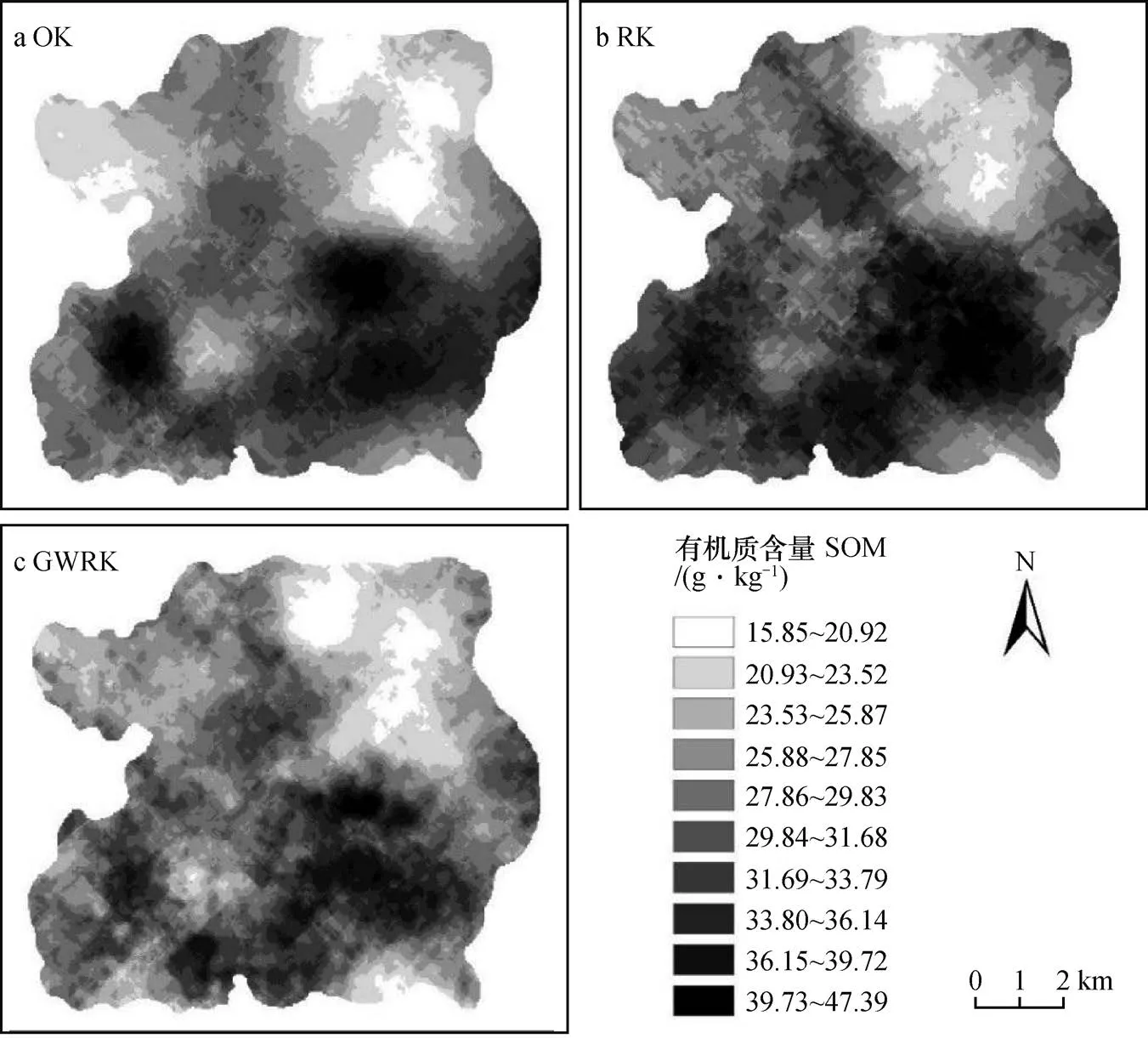
图2 土壤有机质含量空间分布图（a.普通克里格，b.回归克里格，c.地理加权回归克里格）Fig. 2 SOM spatial distribution map interpolated with OK, RK and GWRK

表3 普通克里格、回归克里格和地理加权回归克里格的精度评价Table 3 Comparison between OK, RK and GWRK in precision

研究区地势西高东低，为典型的平原丘陵过渡地带，从高程系数分布图(图3b)可以看出，高程对东北部影响程度最弱，这可能与东北部较为平坦的地势有关；从东北向西南递进，出现了高程对SOM影响程度最大的区域，因为此处正是研究区平原丘陵地貌分界线（200 m）所在的区域，因此也是影响程度最高的区域。坡度的不同引起地表径流强弱的不同，同时坡度较大的地方土地利用类型为林地的可能性最大，地表大量枯枝落叶阻碍了水分的下渗淋溶，树木对径流的缓冲作用也有利于SOM积累［18］，由坡度系数分布图(图3c)可知，西部和东部受坡度影响作用最大，从两侧向中间移动，影响作用逐渐减小，最低值区分布在研究区北部边缘，坡度越小，SOM与坡度空间变化一致性越强，反之随坡度增加，SOM影响因素复杂化，因此坡度对SOM的空间影响权重减小。坡向决定了区域接受太阳辐射的角度和强度，影响光热资源再分配，接受太阳辐射多的区域有机质循环速度快，更有利于SOM积累，研究区坡向的正弦值和余弦值分别代表坡向朝东和朝北的程度，且前者与SOM呈负相关，后者呈正相关，表明研究区西北坡向更有利于有机质的积累，坡向系数分布图(图3d)显示，研究区西北部受坡向影响最大，且从西北部向中部影响逐渐减弱，这与太阳辐射规律吻合。有效铁系数分布图(图3e)(AI)显示，研究区中西部受有效铁影响作用最大，这可能与过渡区高程变化有关，此处向南北两侧影响作用减弱，至东南角处减为最弱，而东北部地势较平坦处受有效铁影响作用中等，且强弱分布较均匀，这是因为在地势平坦处有效铁随径流变化较小，含量分布均匀。容重系数分布图(图3f)和砾石度系数分布图(图3g)的强弱变化规律相似，趋势相反，说明两者对SOM的影响作用相反，容重系数从中心至四周逐渐增大，最小值出现在中心位置，最大值位于研究区边缘，而砾石度系数则是从中心至四周逐渐减小，分布规律相反，由此可知，受土壤容重影响作用强的地方土壤砾石度影响作用弱，呈负相关关系。土壤机械组成［13］（黏粒、粉粒、砂粒）通过土壤的通透性、保水保肥性等影响SOM，尤其是砂粒和黏粒在局部范围对SOM影响作用较为显著，黏粒会影响土壤物理和化学保护机制，黏粒含量越高，土壤对SOM的吸附作用更强，降低SOM矿化速度，有利于SOM积累；砂粒的影响机制恰恰相反，砂粒含量较高的土壤，有机质矿化速度加快，不利于有机质的积累，本研究中黏粒（Clay）对SOM影响作用显著，从黏粒系数分布图(图3h)可以看出，研究区自西北至东南影响作用逐渐减弱，最高值区位于中西部区域，最低值区位于东南部，东北地势平坦区域影响作用变化微弱。

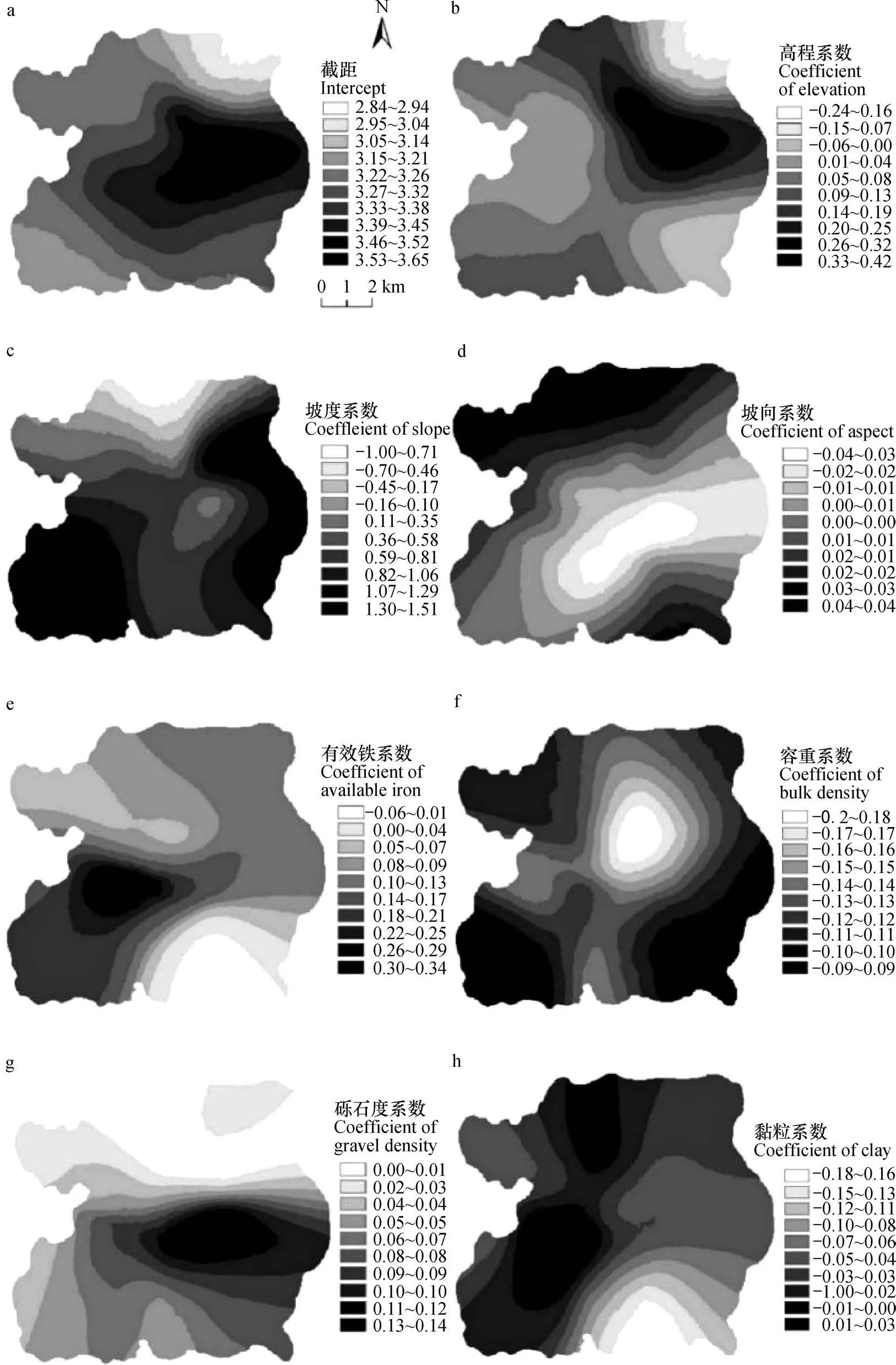
图3 解释变量系数的空间分布图Fig. 3 Spatial distribution of explanatory variable coefficients

3 结 论

土壤有机质是影响土壤肥力的重要指标，掌握其影响因素的变化规律对指导农业生产具有重要意义。本文所选研究区为平原丘陵过渡地带，地形条件复杂，人为活动频繁，运用GWRK对建模集392个采样点建模预测，通过分析得到研究区模型最佳解释变量为：高程、坡度、坡向、有效铁、容重、砾石度、黏粒，且GWRK由于考虑了区域化变量的局部非平稳性，较OK和RK具有更好的预测效果。计算各影响因素权重，并绘制其系数分布图，从图中可以得到各影响因子在不同空间位置对土壤有机质含量的影响和变化规律，从而针对性地采取农业改造措施，在影响因素作用较强的区域重点开展农业设施或局地改造，充分利用地形特点和土壤属性特征，合理开展农业布局，因地制宜地进行农业生产，为实践生产提供参考依据。