基于贝叶斯网络的交通事故原因分析
金宇,王晓峰
(上海海事大学信息工程学院,上海201306)
0 引言
随着我国经济的发展以及汽车保有量的增加,交通事故频繁发生,交通安全问题也越来越受到人们的重视,交通事故的发生虽然具有很大的偶然性和随机性,但其内在还是主要受到人、车、环境等因素的共同作用,通过对过往的数据来分析影响交通事故严重程度的因素,可以对以后道路安全驾驶起到良好的指引作用,为采取措施提供理论依据。
针对交通事故方面的研究,国内外许多学者都进入深入的研究,如苑春苗[3]提出了基于BP神经网络的交通事故分析,并用灵敏度方法研究交通事故因素和严重程度的关系,孙轶轩[2]通过数据挖掘的方法对道路交通事故的致因机理进行分析,运用决策树对交通事故进行了分类研究,建立了事故严重程度模型,AliTava⁃koliKashani[6]利用分类和回归树模型,假定交通事故的独立变量和非独立变量没有关系,从而得出影响交通事故严重程度最重要的独立变量,并得到在两车道和三车道中,未系安全带是影响严重程度最重要的因素。Caner Erden和NumanÇelebi[5]利用粗糙集产生的决策规则来分析交通事故原因之间的联系,大部分都是通过对事故表象的单因素进行孤立的分析,但是交通事故是多方面共同作用的结果,并且各个因素之间可能也是相互关联的,而贝叶斯网络能够全面地揭示各个因素对交通事故的影响,以及各个影响因素之间的联系,更适用于交通事故方面的研究。
1 贝叶斯网络建模方法
1.1 贝叶斯网络节点确定
贝叶斯网络是把某个系统中涉及到的随机变量,根据是否条件独立绘制在一个有向无环图中,是一种概率图模型,根据概率图的拓扑结构,考查一组随机变量及n组条件概率分布。贝叶斯的有向无环图的节点表示随机变量,连接两个节点的边表示两个随机变量的条件依赖关系。贝叶斯公式便是贝叶斯网络的基础,由条件概率公式和全概率公式可以得到。
1.2 贝叶斯网络的结构学习
贝叶斯网络的结构学习就是从给定的数据中学习出贝叶斯网络中每一个节点之间的关系,只有确定了贝叶斯网络的结构才能继续学习贝叶斯网络的参数,目前常用的贝叶斯结构学习方法有以下几种:K2算法、爬山法、模拟退火算法,以及抽样算法等。其中MCMC抽样方法是源于统计物理学和生物学的一类重要的随机抽样算法,MH抽样算法是MCMC方法中常用的抽样算法之一,Madigan等人将MH算法首次引进贝叶斯网络的结构学习,该算法首先要构建一条马尔可夫链,模拟一个收敛于玻尔兹曼的分布,基于“拒绝采样”来接近平稳分布p,算法每次根据上一轮的采样结果xt-1来获取候选样本x*,但是候选样本会有一定的概率不被接受,假定从xt-1到 x*的转移概率为,其中是预先知道的先验概率,是xt被接受的概率,当达到平稳状态p时有因此设置转移概率能够使马尔可夫链达到平稳过程。
Metropolis-Hastings算法
输入:先验概率Q(x*|xt-1)
1. 初始化x0
2. for t=1,2...do
3. 根据先验概率选出候选样本
4. 从均匀分布(0,1)范围选出阈值
5. ifu≤A(x*|xt-1)then
6. xt=x*
7. else xt=xt-1
8. end if
9. end for
10.返回采样出的样本序列x1,x2,…,xn
1.3 贝叶斯网络的参数学习
贝叶斯网络的参数学习是在贝叶斯网络结构已经知道的情况下,基于数据对网络中的各个属性进行条件概率的计算,目前参数学习的主要方法有贝叶斯估计法和最大似然估计法,两种估计方法都要满足样本是独立同分布的,两者不同之处在于贝叶斯估计还利用了参数的先验知识,通过先验概率得到参数的估计值,理论上比极大似然估计更准确,贝叶斯估计的基本思想是:给定完整的数据集d和一个含有未知参数的分布,θ是有先验分布p(θ)的随机变量,则p(θ|d)是θ的后验概率,而贝叶斯参数学习的就是p(θ|d),因为Dirichlet分布的共轭性可以减少计算的复杂度,所以p(θ)通常都使用Dirichlet分布。
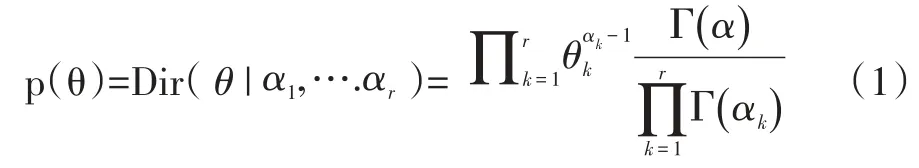
所以参数θ的后验分布为:

2 事故原因的贝叶斯建模
本文的数据集来源于美国阿勒格尼县2014年到2016年的82913条交通事故,表中属性有受伤人数、是否有死亡、车辆类型、发生时间、光照强度、天气状况、路面状况、碰撞地点、道路类型、是否饮酒、交通控制方式、是否拨打手机、是否为节假日、路口类型、碰撞车辆数目、首先对数据进行筛选,并对交通事故发生的层面进行多维度的分析,发现交通事故发生的原因主要集中在人为因素、环境因素和车辆因素等,理论上来说选取的属性变量的越多,建模得到的结果更接近交通事故分析的机理,但是属性变量的增多会增加建模的分析难度,为了平衡建模复杂度和预测精度的关系,经过初步筛选,本文选取受伤人数和是否有人死亡作为决策变量,其他因素设置为属性变量,给不同的属性的不同取值设置编码,为了符合建模要求,也将一些连续型的属性处理成离散变量,详细的编码情况如下表所示,其中每一个属性名称都对应贝叶斯网络中的一个节点。

表1 事故因素编码表
基于MCMC算法,应用MATLAB的Full-BNT工具箱进行贝叶斯网络结构的学习,首先导入事故的数据集,经过贝叶斯结构学习得到各个属性的关联矩阵,再对属性进行筛选,根据关联矩阵绘制出各个属性之间的关系,最终确定了贝叶斯网络的结构,属性之间的关系如图1所示。
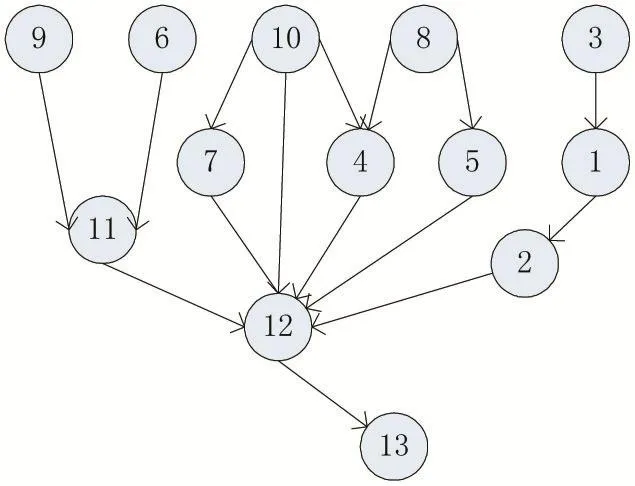
图1 贝叶斯网络结构图
1-是否用手机2-是否饮酒3-是否工作日4-光照条件5-路口类型6-碰撞地点类型7-路面状况8-道路类型9-交通方式10-天气11-车辆数12-受伤人数13-是否有死亡
已经得到贝叶斯网络的结构,就可以应用贝叶斯估计对贝叶斯网络进行参数学习,因为死亡人数与受伤人数的关联比较大,所以本文主要分析了受伤人数以及是车辆碰撞数目两个变量的参数学习效果。

表2 受伤人数与天气之间的条件概率
首先分析的是交通事故受伤人数与天气状况之间的关系,也对比了贝叶斯网络参数学习的结果和实际结果,可以发现贝叶斯网络具有很高的精确度,依据表2可以发现,天气状况良好时,并且发生交通事故时,没有人受伤的概率是最小的,当天气为下雪时,发生事故受伤比例越少,也从侧面反映出当天气状况恶劣时,人们更注意自己的行车安全,从而发生事故时,相应的损失也会更少。

表3 道路类型、交通控制、车辆碰撞数目的条件概率
由表3可知,在道路类型一定情况下,当有交通控制时,虽然交通事故的数目减少,但是发生两车碰撞的概率增加,单机动车发生事故的几率大大减少,在交通控制一定的情况下,在国道和省道发生大型交通事故的可能性更大,这也符合人们一般的经验常识,因此在国道和省道上行驶的车辆数目更多,应当更加注意交通控制的方式,减少事故发生的概率。
3 结语
本文通过对以往历史交通事故数据进行分析,得出交通事故是环境-人-车辆-道路多种因素共同作用的结果,通过多方面的分析和MCMC算法,选取合适的属性,建立贝叶斯模型,用有向无环图形象表示和挖掘出各个属性之间的联系,使之更符合人的思维特征和推理形式,体现了各个属性之间的层次关系,对交通事故进行分析只是保证安全出行的一方面,更需要交管部门的监管和驾驶员自身安全意识的提高,通过本文的分析,对以后指导交通驾驶和安全出行都提供了很好的借鉴意义。

